Uma nova solução para o paradoxo de Fermi (por que estamos sozinhos no universo)

Recentemente, eu vim com uma solução completamente nova para o Fermi Paradox . Não vou recontar o que você pode ler no wiki.



Vou passar direto ao ponto. Para resolver o problema, precisamos de alguns ingredientes.

1. MWI - a interpretação do multiverso.

Uma coisa da ciência popular bastante conhecida e explicada (muitas vezes incorretamente). Resumidamente, no MWI o mundo é "inteiramente" determinado, não há acidente. Quando os eventos têm vários resultados, todos acontecem e, então, usando o mecanismo de decoerência, diferentes "ramos" da realidade aparecem em nosso macro-mundo, onde diferentes cópias de nossa consciência falham. No entanto, cada cópia se considera a única, pois não há interação entre ramificações.

2. Suicídio Quântico

A idéia interessante e controversa do suicídio quântico é baseada no MWI. Digamos, se o tiro da arma depender do evento quântico, então, depois de colocar uma arma na cabeça, não perderemos nada: no ramo em que a arma disparou, deixaremos de existir e onde não disparamos, continuamos a existir. Ou seja, nossa consciência "cai" no ramo onde o tiro não aconteceu.

O suicídio quântico é frequentemente criticado pelo seguinte motivo - e se a morte de um tiro não for instantânea? Mas e se não morrermos, mas permanecermos paralisados? Abaixo retornaremos a esta edição.

3. Catástrofe a vácuo (decaimento do falso vácuo)

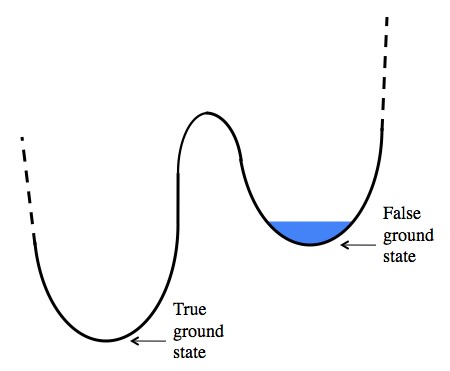
É possível que nosso vácuo seja falso , ou seja, nosso vazio não seja um estado inferior de vácuo (no sentido energético). Então, é possível uma transição espontânea em algum momento do vácuo para um estado de energia mais favorável. A diferença na energia do vácuo se transforma em uma confusão de uma variedade de partículas (e possivelmente não existe em nosso vácuo), e seu número é enorme. Na verdade, o assunto que existia antes desse evento pode ser negligenciado.

Além disso, quando o centro de destruição surgiu, é impossível interromper o processo, como o dominó, o processo se espalha em todas as direções e à velocidade da luz! Ou seja, ele não tem precursores - nem música perturbadora, como nos filmes. Você senta, bebe vinho à noite e olha para as estrelas e depois uma vez - e não há nada além de um plasma de novas partículas.

Gostaríamos de acreditar que esse evento é muito, muito, muito improvável, por exemplo, Nick Bostrom me respondeu com um link para seu artigo com Tegmark, onde eles estimaram a probabilidade de um evento desse tipo "de cima":

arxiv.org/abs/astro-ph/0512204

Fator Doom.

Você já reparou que a catástrofe a vácuo é muito mais adequada ao suicídio quântico do que uma arma? O processo é instantâneo, não pode deixá-lo aleijado ... É simplesmente perfeito. E então ... E se isso acontecer regularmente, mas não percebermos? Eu gostaria de considerar exatamente esse universo.

Vamos introduzir o valor D (fator doom), que é proporcional à probabilidade de decaimento espontâneo do vácuo. Para D = 1, um desses eventos ocorre uma vez por ano em um cubo de ano-luz 1x1x1. Os astrônomos agora estão empolgados em usar o ano-luz como uma medida de distância, em vez do parsec, mas, neste caso, eu realmente quero medir tempo e distância em unidades "idênticas".

Universo Condenado

Então, qual é a probabilidade de permanecermos vivos nesse universo? Precisamos estimar o número de possíveis desastres no passado, ou seja, em nosso cone de luz do passado. Este valor é igual ao volume de um cone quadridimensional da altura t, se as distâncias forem medidas em anos-luz e o tempo for simplesmente em anos (c = 1):

$$

Para nossa história, o tempo nesta fórmula deve ser substituído por A = 13,8 bilhões de anos - a idade do Universo. (na verdade, isso não é totalmente honesto, já que mais perto da época do Big Bang, o cone está distorcido devido ao GR, mas ignoramos esses efeitos aqui)

Oh sortudo!

Pedindo $$ temos n = 379 milhões. Ou seja, a probabilidade de não morrermos é igual a $$ . Isso não deveria nos surpreender, no MWI as filiais são separadas ainda mais em minutos e segundos.

No entanto, é interessante rastrear e quando (em média) foi o último evento desse tipo? Isso pode ser feito pela fórmula:

$$

O valor que obtemos é bastante estranho (para a aleatoriedade D escolhida por nós) - cerca de 100 milhões de anos. No entanto, de fato, isso não é surpreendente, uma vez que os 4 volumes do cone crescem muito rapidamente até a base. Ou seja, o perigo que nos espera não vem do vácuo acidentalmente colapsado há quatro anos em Alpha Centauri, mas do fato de sermos cobertos por uma onda de decomposição que nos atingiu das profundezas do universo.

Com que rapidez decompomos?

Para estimativa, tomamos a derivada de n com relação a te obtemos:

$$

Para o nosso valor de D, o valor de n aumenta 0,11 a cada ano, ou seja, a cada 9 anos, nossas chances são reduzidas pela metade (mas, novamente, não percebemos isso para nenhum valor de D!)

Argumento do Dia do Juízo Final

Mais uma vez, não vou recontar o wiki . No entanto, esse argumento opera com disposições (mal definidas) sobre 'almas' que 'infundem' (temporalmente) aleatoriamente nos corpos existentes. Como os corpos são muito maiores até o final da civilização, a probabilidade de nascer no Império Romano é muito pequena.

No entanto, se o número de corpos é normalizado pela probabilidade da existência de ramos da realidade (e deveria normalizar-se assim - caso contrário, a regra de Bourne não funcionaria), a distribuição 'corrigida' do número de corpos tem um pico no início dos tempos, e não no final, ou seja, invertendo este argumento:



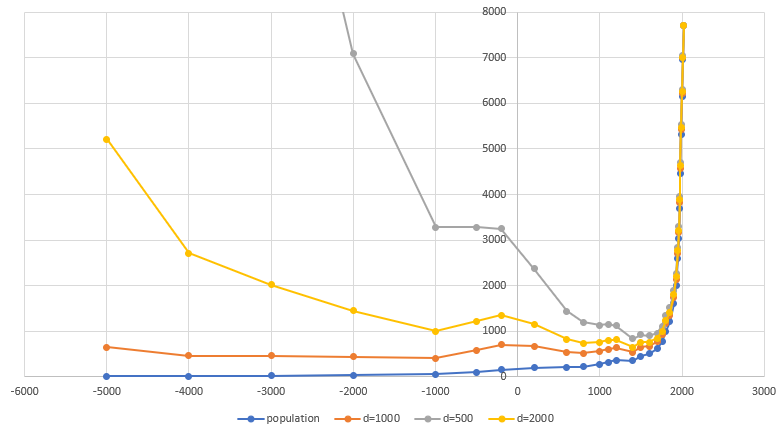
A linha azul no gráfico mostra a população mundial em milhões de pessoas em momentos diferentes. Outras curvas 'normalizam' esses valores, considerando que a amplitude da probabilidade no passado era maior (para valores menores de D, por exemplo, d = 1000 - a probabilidade diminui pela metade em 1000 anos, e não em 9 anos)

Paradoxo de Fermi

Finalmente, chegamos ao próprio paradoxo. Aplicamos o argumento do dia do juízo invertido às civilizações (além disso, quando o tempo de desenvolvimento de diferentes civilizações diverge em milhões de anos, o efeito começa a aparecer a partir de valores D muito mais baixos). Ou seja, a probabilidade de nascer na civilização tardia é insignificante.

Ou seja, nascemos na primeira e até agora a única civilização!

Enquete

O artigo da wiki fornece várias soluções para o problema. Vote naqueles que você acha que são prováveis. Peguei as opções da versão em inglês do Wiki (existem poucas na versão russa), mas combinei algumas