Métodos quase-newtonianos ou quando existem muitas segundas derivadas para Athos

No primeiro conhecimento dos métodos quase-newtonianos, podemos nos surpreender duas vezes. Em primeiro lugar, após uma rápida olhada nas fórmulas, surgem dúvidas de que isso possa funcionar. No entanto, eles trabalham. Além disso, parece duvidoso que eles funcionem bem. E é ainda mais surpreendente ver quão rápido eles são do que as várias variações da descida do gradiente, não em tarefas especialmente construídas, mas em tarefas reais tiradas da prática. E se, depois disso, ainda houver dúvidas misturadas com o interesse, você precisará entender por que isso funciona de alguma maneira.

A origem e as idéias básicas que orientam os métodos de gradiente, incluindo o método de Newton, já foram consideradas . Nomeadamente, contamos com as informações sobre o comportamento da função nas proximidades da posição atual, o que nos fornece uma análise matemática simples. No mínimo, foi assumido que as informações sobre os primeiros derivativos estavam disponíveis para nós. E se isso é tudo o que está disponível para nós? A descida de gradiente é nossa sentença? Claro, sim, a menos que você se lembre de repente de que estamos lidando com um processo no qual a função objetivo é processada adequadamente. E se sim, por que não usamos as informações acumuladas sobre o comportamento da função para tornar nossa caminhada em sua superfície um pouco menos cega?

A idéia de usar informações sobre o caminho coberto está no cerne de muitas maneiras de acelerar os métodos de descida. Este artigo discute uma das maneiras mais eficazes, embora não a mais barata, de contabilizar esse tipo de informação, levando à idéia de métodos quase-newtonianos.

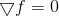
Para entender de onde crescem as pernas dos métodos quasi-newtonianos e de onde vem o nome, precisamos voltar ao método de minimização com base na solução direta da equação de ponto estacionário . Assim como a consideração do método de Newton aplicado à solução dessa equação nos levou ao método de otimização com o mesmo nome (que, diferentemente de seu progenitor, possui uma região global de convergência), podemos esperar que a consideração de outros métodos para resolver sistemas de equações não lineares seja proveitosa. planejar idéias para criar outros métodos de otimização.

Métodos secantes

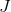
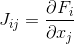
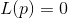
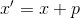
Deixe-me lembrá-lo de que o método de Newton para resolver o sistema de equações , baseia-se na substituição na vizinhança de algum ponto próximo à solução as funções sua aproximação linear onde É um operador linear que, quando é um vetor e possui derivadas parciais em relação a cada variável, coincide com a matriz de Jacobi . Em seguida, a equação é resolvida e apontar tomado como uma nova aproximação à solução desejada. É simples e funciona.

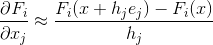
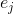
Mas e se, por algum motivo, não pudermos calcular a matriz de Jacobi? A primeira coisa que vem à mente nesse caso é que, se não podemos calcular analiticamente as derivadas parciais, podemos obter uma aproximação numérica para elas. A opção mais simples (embora não seja a única) para essa aproximação pode ser a fórmula das diferenças finitas corretas: onde É o j-ésimo vetor base. A matriz composta por tais aproximações será denotada por . 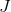Uma análise de quanto de reposição em no método de Newton, sua convergência afeta, um número bastante grande de obras é dedicado, mas, neste caso, estamos interessados ​​em outro aspecto. Nomeadamente, essa aproximação requer o cálculo da função em N pontos adicionais e, além disso, a função nesses pontos interpola a função , ou seja,



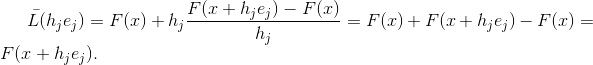
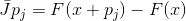
Nem toda aproximação da matriz de Jacobi tem essa propriedade, mas toda matriz de uma função afim que possui essa propriedade é uma aproximação da matriz de Jacobi. De fato, se e então às . Essa propriedade, ou seja, a propriedade de interpolação, nos fornece uma maneira construtiva de generalizar o método de Newton.

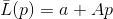
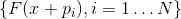
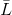
Vamos - função que satisfaça a exigência para algum sistema de vetores linearmente independentes . Então, essa função é chamada de função secante , e a equação que a define é a equação secante . Se o sistema de vetores está completo (ou seja, existem exatamente N deles e eles ainda são linearmente independentes) e, além disso, o sistema de vetores linearmente independente então definido exclusivamente.

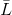
Qualquer método baseado na mudança local da equação equação da forma onde satisfaz a equação secante , chamada método secante .

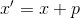
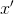
Surge uma pergunta justa sobre como construir o secante para uma função da maneira mais racional. . A seguinte linha de raciocínio parece óbvia: seja construído um modelo afim no ponto x que interpola a função dada nos pontos . Solução de equação nos dá um novo ponto . Em seguida, para construir um modelo afim em um ponto é mais razoável escolher pontos de interpolação para que o valor já conhecido - ou seja, tire-os do conjunto . 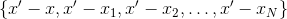Existem diferentes opções para quais pontos escolher entre os muitos usados ​​anteriormente. 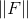Por exemplo, você pode tomar como pontos de interpolação aqueles em que importa menos ou apenas o primeiro pontos. De qualquer forma, parece óbvio que deve ser incluído em muitos pontos de interpolação para o novo modelo afim. 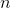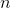Tão além etapas do processo iterativo em nosso conjunto podem ser de até deslocamentos construídos em pontos passados ​​anteriormente. Se o processo for construído de tal maneira que o novo modelo afim não use mais dos valores anteriores, esse processo é chamado de método secante do ponto p.

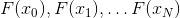
À primeira vista, pode parecer que o método secante do ponto N é o melhor candidato para o papel de substituir o método Newton, uma vez que faz o máximo uso das informações que obtemos no processo de solução, minimizando o número de cálculos adicionais - usamos o valor da função no último N pontos passaram. Infelizmente, isso não é verdade. O problema é que o sistema vetorial teimosamente se recusa a ser linearmente independente com um N. suficientemente grande. Além disso, mesmo que essa condição seja cumprida e o modelo afim correspondente ainda exista, é possível que as direções também provam ser linearmente independentes, resulta ainda menos. E isso implica o fato de que o modelo afim, embora exista, é degenerado e praticamente inadequado.

Em geral, o mais estável é o método secante de 2 pontos. Ou seja, um método no qual a cada iteração temos que calcular valores N-1 adicionais da função. Claramente, isso não é adequado para nossos propósitos práticos.

Então a questão é - o que foi tudo isso?

Métodos quase-newtonianos para resolver equações

A saída é simples, embora não óbvia. Se não tivermos a capacidade técnica, com base nos valores já calculados, de determinar exclusivamente o modelo afim que satisfaz a equação secante, isso não será necessário. Tomamos a equação de secantes como base, mas exigiremos que ela seja satisfeita apenas para algum sistema incompleto de vetores . Em outras palavras, exigiremos que a condição de interpolação seja satisfeita apenas para um número suficientemente pequeno de valores conhecidos. Obviamente, nesse caso, não podemos mais garantir que a matriz usada nesse modelo tenderá à matriz de Jacobi, mas não precisaremos disso. Além disso, o modelo afim deve interpolar a função no ponto atual, ou seja, , obtemos a seguinte formulação do método secante:



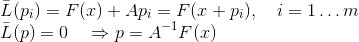
Bruiden foi o primeiro a considerar métodos desse tipo para m = 1, chamando-os quase-newtonianos. É claro que a condição secante, neste caso, nos permite identificar exclusivamente a matriz somente se condições adicionais lhe forem impostas e cada uma dessas condições adicionais der origem a um método separado. O próprio Bruyden argumentou da seguinte maneira:

como o movimento na direção do ponto direto ao ponto não nos fornece nenhuma informação adicional sobre como a função muda, exceto direções, então o efeito da nova função afim no vetor deve diferir do efeito da função antiga no mesmo vetor, quanto menos diferente de . Como último recurso, quando ortogonal , o comportamento da nova função não deve ser diferente do comportamento da antiga.

A ideia de Breiden é brilhante em sua simplicidade. De fato, se não temos novas informações sobre o comportamento da função, o melhor que podemos fazer é tentar não sujar a antiga. Então a condição adicional

para todos tal que

permite determinar exclusivamente a matriz da nova transformação - é obtida adicionando uma correção de classificação 1 à matriz antiga.



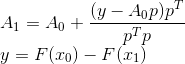
No entanto, apesar da simplicidade e consistência das conclusões de Bruiden, elas não fornecem o ponto de apoio que poderia servir de base para a construção de outros métodos semelhantes. Felizmente, há uma expressão mais formal de sua ideia. Ou seja, a matriz construída dessa maneira É a solução para o seguinte problema:



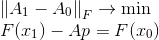
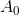
A restrição de tarefa nada mais é do que a equação secante, e a condição de minimização reflete nosso desejo de salvar o máximo de informações possível na matriz . A medida da discrepância entre as matrizes nesse caso é a norma de Frobenius, na qual o problema apresentado tem uma solução inequívoca. Esta formulação pode muito bem servir como ponto de partida para a construção de outros métodos. Ou seja, podemos alterar tanto a medida pela qual avaliamos as mudanças introduzidas quanto as condições impostas à matriz. Em geral, já é possível trabalhar com essa formulação do método.

Métodos de otimização quase-Newton

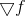
Tendo entendido a idéia principal, podemos finalmente voltar aos problemas de otimização e perceber que aplicar a fórmula de Bruyden para recalcular o modelo afim não se encaixa muito bem em nossa tarefa. De fato, a primeira derivada da função gradiente não há mais nada além da matriz hessiana, que por construção é simétrica. 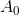Ao mesmo tempo, a atualização de acordo com a regra de Bruyden leva a uma matriz assimétrica mesmo que era simétrico. Isso não significa que o método Bruden não possa ser aplicado para resolver a equação do ponto estacionário, mas com base nessa regra de atualização, é improvável que consigamos construir bons métodos de otimização. Em geral, é bastante óbvio que o método quase-Newton deve funcionar melhor, mais precisamente o sistema de condições do problema descreve as especificidades de uma matriz Jacobi específica.

Para corrigir essa desvantagem, adicionamos uma restrição adicional ao problema de minimização de Bruden, exigindo explicitamente que a nova matriz seja simétrica junto com a antiga:



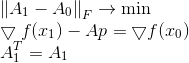
A solução para esse problema é



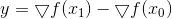
Aqui , e a fórmula de recálculo da matriz recebe o nome de seus criadores - Powell, Shanno e Bruyden (PSB). A matriz resultante é simétrica, mas claramente não é positiva definida, mesmo que de repente não será colinear . E vimos que a certeza positiva é altamente desejável nos métodos de otimização.

Novamente, corrigiremos a condição do problema, usando desta vez a norma de Frobenius em escala como uma medida da divergência da matriz.



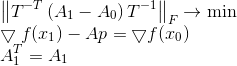
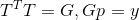
A origem de tal afirmação da pergunta é um grande tópico separado, mas é interessante que, se a matriz T for tal que (ou seja, G também é uma matriz de transformação afim que satisfaz a equação secante para a direção p), a solução para esse problema acaba sendo independente da escolha de T e leva à fórmula de atualização



conhecida como a fórmula de Davidon-Fletcher-Powell. Esse método de atualização se comprovou na prática, pois possui a seguinte propriedade:

se e 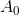positivo definitivo então também identificado positivamente.

Observo depois que, se a primeira condição não for cumprida, não existe uma função afim com uma matriz definida positiva que satisfaça a equação secante.

Se no problema que leva ao método DFP, tomamos, como medida da discrepância de modelos afins, a distância não entre as próprias matrizes, mas entre as matrizes inversas a elas, obtemos um problema da forma



Sua solução é uma fórmula conhecida, descoberta quase simultaneamente por Breiden, Fletcher, Goldfarb e Shanno (BFGS).



Até o momento, acredita-se que o recálculo de acordo com essa fórmula seja o mais eficiente do ponto de vista computacional e, ao mesmo tempo, seja menos propenso à degeneração da matriz com um grande número de iterações. Nas mesmas condições do DFP, essa fórmula preserva a propriedade de definição positiva.

Todos os métodos descritos para atualizar a matriz requerem uma correção da classificação 2. Isso facilita e facilita a inversão da matriz usando a fórmula de Sherman-Morrison e o valor .



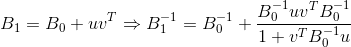
desde que o denominador da fórmula seja diferente de zero. Não darei fórmulas específicas para atualizar as matrizes inversas dos métodos listados, pois são fáceis de encontrar ou derivar independentemente. A única coisa que deve ser notada nesse caso é que as variantes dos métodos com atualização da matriz inversa são geralmente muito menos estáveis ​​(ou seja, sofrem mais com erros de arredondamento) do que aquelas que sugerem atualizar a matriz original. É mais eficaz atualizar não a matriz em si, mas sua decomposição de Cholesky (a não ser, é claro, que tal decomposição ocorra), pois essa opção de implementação é mais numericamente estável e, além disso, minimiza o custo de resolver uma equação que determina a direção do movimento.

Resta considerar a questão de como deve ser a primeira matriz no processo quase-newtoniano. Tudo é óbvio aqui - quanto mais próximo estiver da matriz hessiana ou de sua versão corrigida, se o hessiano não se mostrar de repente definido positivamente, melhor será do ponto de vista da convergência. No entanto, em princípio, qualquer matriz definida positiva pode ser adequada para nós. A versão mais simples dessa matriz é única e, em seguida, a primeira iteração coincide com a iteração da descida do gradiente. Fletcher e Powell mostraram (naturalmente, para o método DFP) que se a função quadrática for minimizada, independentemente de qual matriz (definida positiva) seja usada como a iteração inicial do DFP, elas levarão a uma solução exatamente em N iterações, onde N é dimensão do problema, e a matriz quasi-newtoniana coincide com a matriz hessiana no ponto mínimo. No caso geral não-linear dessa felicidade, é claro que não esperaremos, mas isso pelo menos dá motivos para não se preocupar muito com a má escolha da matriz inicial.

Conclusão

A abordagem descrita para a construção de métodos quase-newtonianos não é a única possível. No mínimo, os descobridores dos métodos quase-newtonianos descritos e muitos pesquisadores subsequentes adotaram as mesmas fórmulas com base em considerações completamente diferentes. No entanto, é interessante que, assim que apareceu um certo método quase newtoniano, ficou claro, após pouco tempo, que era uma solução para algum problema de otimização facilmente interpretado. Na minha opinião, é notável que seja possível trazer algum denominador comum para métodos tão diversos, pois isso fornece a base para a construção de outros métodos que melhor levam em conta as especificidades de uma tarefa específica. Em particular, existem métodos quase newtonianos projetados para atualizar matrizes esparsas, métodos nos quais o menor número possível de elementos está sujeito a alterações, e muitos outros seriam uma fantasia.

Deve-se notar também que os métodos de métricas variáveis, apesar do nome, nem sempre levam à construção de matrizes, que na verdade são métricas, embora o façam sempre que for possível. , , — , - . , , . , . , — .

, . , ( , , N , , ). ( , , ), . , , — . — .