Dentro do JeMalloc. Estruturas de dados principais: emparelhando heap e árvore de bitmap

O tema dos Alocadores geralmente aparece na Internet: de fato, um Alocador é uma espécie de pedra angular, o coração de qualquer aplicativo. Nesta série de posts, quero falar em detalhes sobre um alocador muito divertido e eminente - o JeMalloc , suportado e desenvolvido pelo Facebook e usado, por exemplo, na biônica [Android] lib C.

Na rede, não consegui encontrar nenhum detalhe que revelasse totalmente a alma desse alocador, o que acabou afetando a impossibilidade de tirar conclusões sobre a aplicabilidade do JeMalloc na solução de um problema específico. Muito material foi publicado e, para lê-lo, não foi cansativo, proponho começar com o básico: Estruturas básicas de dados usadas no JeMalloc.

Debaixo do gato, eu estou falando sobre Pairing Heap e Bitmap Tree , que formam a base do JeMalloc. Nesta fase, não toco no tópico multithreading e Fine Grained Locking ; no entanto, continuando a série de postagens, definitivamente vou falar sobre essas coisas, para o qual, de fato, vários tipos de Exóticos são criados, em particular o descrito abaixo.

Bitmap_s é uma estrutura de dados semelhante a uma árvore que permite:

• Encontre rapidamente o primeiro bit configurado / não configurado em uma determinada sequência de bits.
• Altere e obtenha o valor de um bit com o índice i em uma determinada sequência de bits.
• A árvore é construída de acordo com uma sequência de n bits e possui as seguintes propriedades:
• A unidade base da árvore é o nó e a unidade base do nó é o bit. Cada nó consiste em exatamente k bits. O número de bits de um nó é selecionado para que as operações lógicas em um intervalo selecionado de bits sejam calculadas o mais rápida e eficientemente possível em um determinado computador. No JeMalloc, um nó é representado por um tipo longo não assinado .
• A altura da árvore é medida em níveis e para uma sequência de n bits é H = $$$\ log_ {k} {n} registro k (n)$níveis.
• Cada nível da árvore é representado por uma sequência de $$$countOfNodesOnLevel = integerCeil (\ frac {n} {{k} ^ {H - currentLevel + 1}})$nós, o que equivale a uma sequência de $$$countOfBitsOnLevel = countOfNodesOnLevel * k$pouco.
• O nível mais alto (raiz) da árvore consiste em k bits e o mais baixo - de n bits.
• Cada bit de um nó de nível L determina o estado de todos os bits de um nó filho de nível L - 1: se um bit estiver definido como ocupado, todos os bits de um nó filho também serão configurados como ocupado, caso contrário, os bits de um nó filho poderão ter estado 'ocupado' e 'livre'.

É razoável representar bitmap_t em duas matrizes: a primeira de uma dimensão igual ao número de todos os nós da árvore - para armazenar os nós da árvore e a segunda da dimensão da altura da árvore - para armazenar o deslocamento do início de cada nível na matriz dos nós da árvore. Com esse método de especificação de uma árvore, o elemento raiz pode ir primeiro e, em seguida, em sequência, os nós de cada um dos níveis. No entanto, os autores do JeMalloc armazenam o último elemento raiz na matriz e, à frente dele, os nós dos níveis subjacentes da árvore.

Como um exemplo ilustrativo, considere uma sequência de 92 bits e K = 32 em mente. Assumimos que o estado é 'livre' - indicado por um único bit, e o estado 'ocupado' - zero. Suponha também que, na sequência de bits original, o bit com índice 1 (contando de zero, da direita para a esquerda na figura) esteja definido para o estado ocupado. Então bitmap_t para essa sequência de bits será semelhante à imagem abaixo:



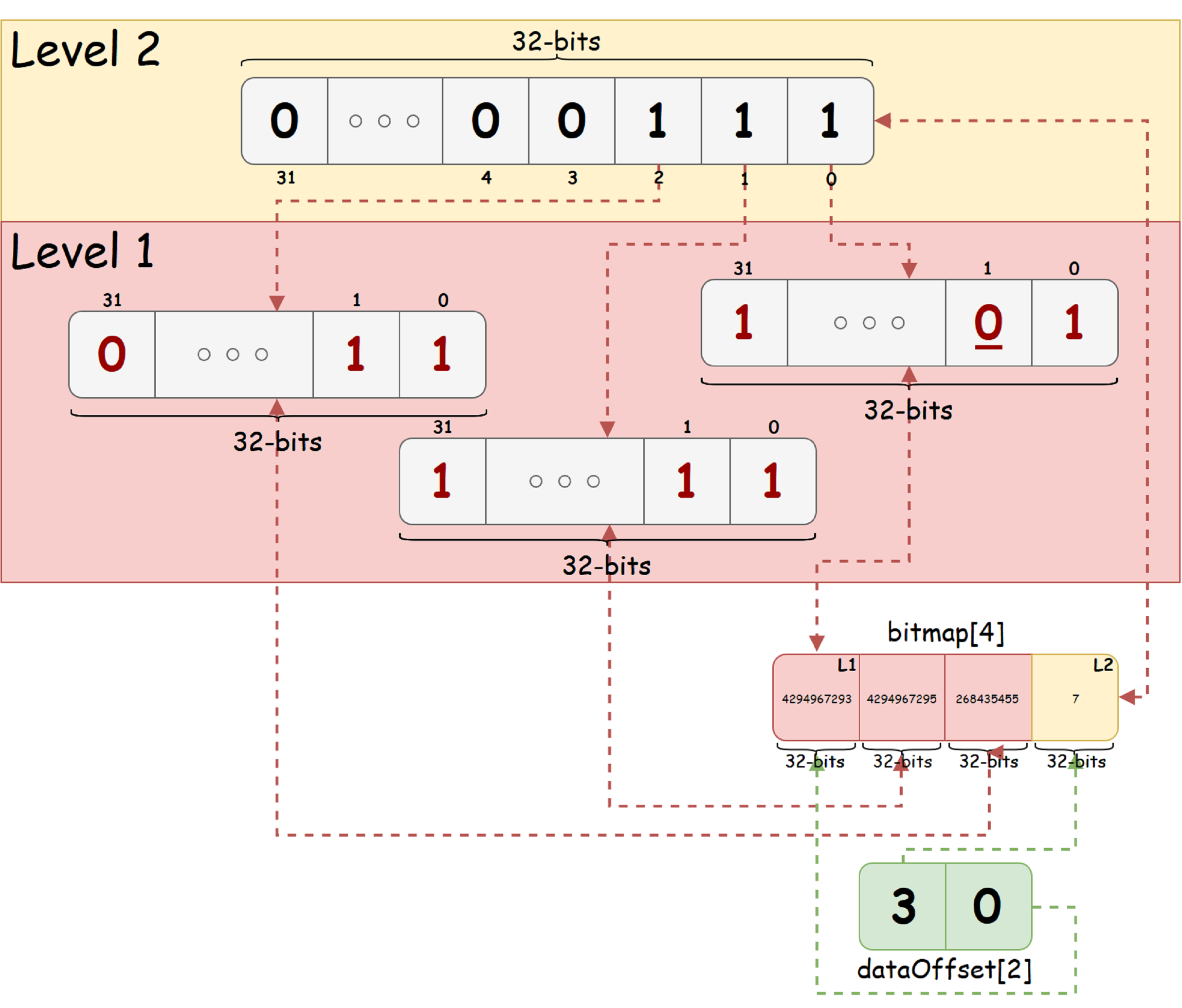A partir da figura, vemos que a árvore resultante possui apenas dois níveis. O nível raiz contém 3 bits de unidade, o que indica a presença de bits livres e ocupados em cada um dos nós filhos do bit correspondente. No canto inferior direito, é possível ver a visualização em árvore em duas matrizes: todos os nós da árvore e deslocamentos de cada nível na matriz de nós.

Supondo que bitmap_t seja representado por duas matrizes (uma matriz de dados e uma matriz de compensações no nível da árvore na matriz de dados), descrevemos a operação de encontrar o primeiro bit menos significativo em um dado bitmap_t:

• A partir do nó raiz, realizamos a operação de busca pelo primeiro bit menos significativo do nó: para resolver esse problema, os processadores modernos fornecem instruções especiais que podem reduzir significativamente o tempo de busca. Vamos salvar o resultado encontrado na variável FirstSetedBit .
• A cada iteração do algoritmo, manteremos a soma das posições dos bits encontrados: countOfSettedBits + = FirstSetedBit
• Usando o resultado da etapa anterior, vamos para o nó filho do primeiro bit de unidade menos significativo do nó e repetimos a etapa anterior. A transição é realizada de acordo com a seguinte fórmula simples: $$$currentNode = bitmapData [levelOffsetArray [currentLevel] + sumOfBits]$
• O processo continua até que o nível mais baixo da árvore seja atingido. countOfSettedBits - o número do bit desejado na sequência de bits de entrada.

O emparelhamento de heap é uma estrutura de dados de árvore semelhante a heap que permite:

• Insira um elemento com complexidade de tempo constante de O (1) e custo amortizado de O (log N) ou O (1) , dependendo da implementação.
• Pesquise pelo menos o tempo constante - O (1)
• Mesclar dois heap de emparelhamento com complexidade de tempo constante - O (1) e custo amortizado O (log N) ou O (1) - dependendo da implementação
• Excluir um elemento arbitrário (em particular, um mínimo) com uma estimativa de complexidade temporária em O (N) e uma estimativa de complexidade amortizada em O (log N)

Mais formalmente, Pairing Heap é uma árvore arbitrária com uma raiz dedicada que satisfaz as propriedades da pilha (a chave de cada vértice não é menos / não é mais do que a chave de seu pai).
Um heap de emparelhamento típico, no qual o valor do nó filho é menor que o valor do nó pai (também conhecido como heap de emparelhamento mínimo) se parece com isso:



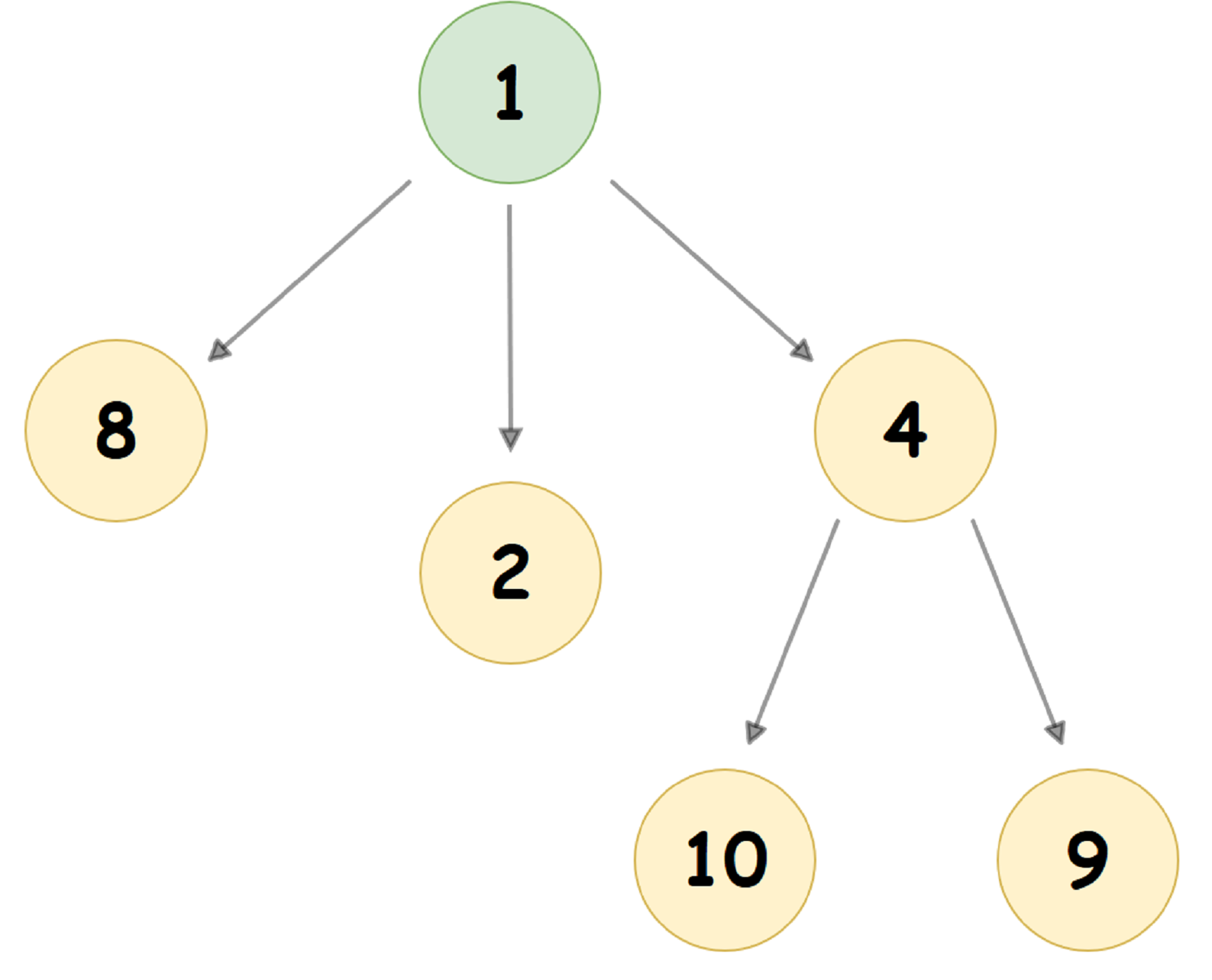
Na memória do computador, Pairing-Heap, como regra, é apresentado de uma maneira completamente diferente: cada nó da Árvore armazena 3 ponteiros:

• Ponteiro para o nó filho mais à esquerda do nó atual
• Ponteiro para o irmão esquerdo do nó
• Ponteiro para o irmão direito do nó

Se algum dos nós indicados estiver ausente, o ponteiro do nó correspondente será anulado.
Para o heap apresentado na figura acima, obtemos a seguinte representação:



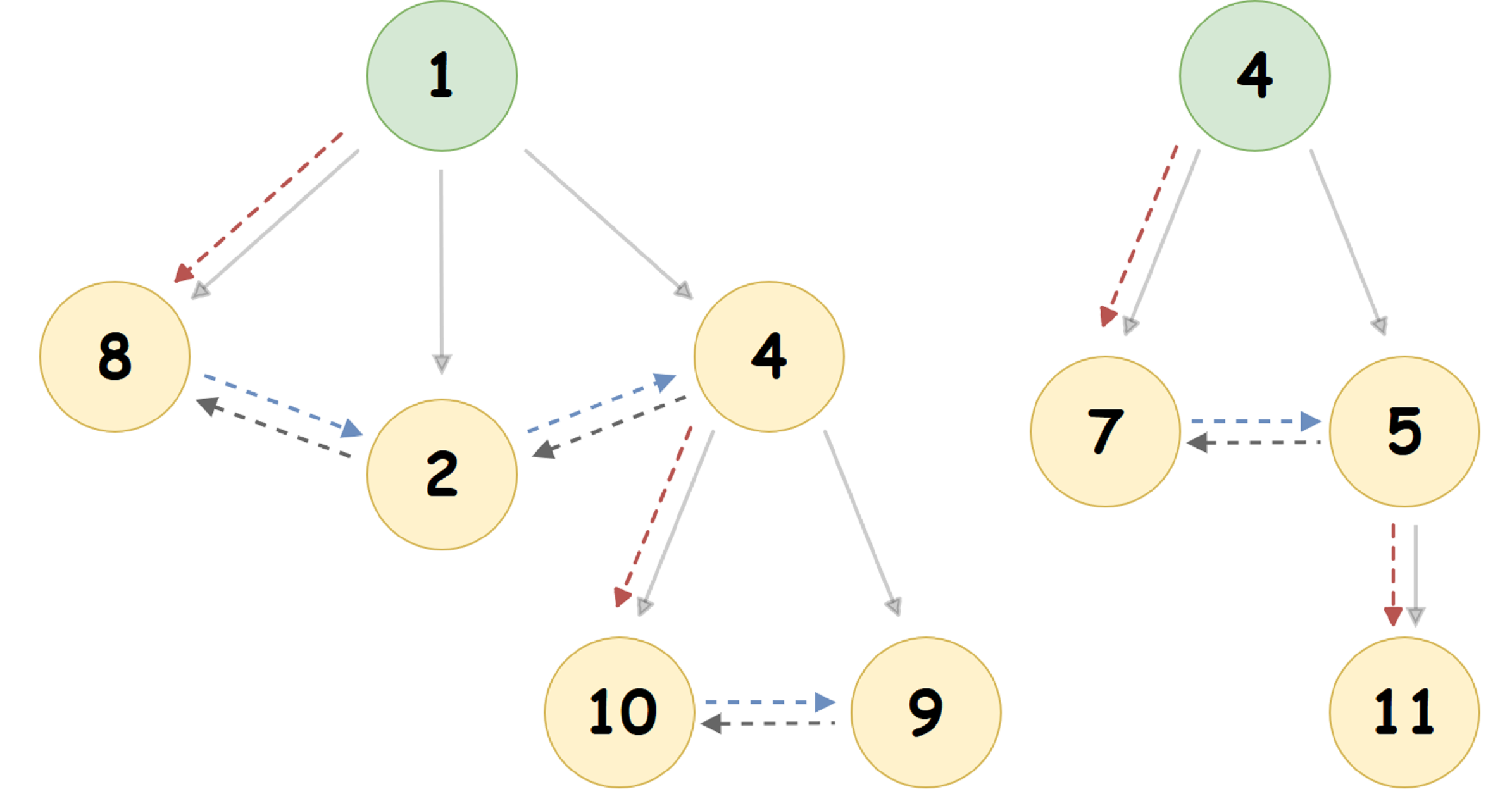Aqui, o ponteiro para o nó filho mais à esquerda é indicado por uma seta pontilhada vermelha, o ponteiro para o irmão direito do nó é azul e o ponteiro para o irmão esquerdo é cinza. A seta sólida mostra a representação de Heap de emparelhamento em uma forma de árvore comum a uma pessoa.

Observe os dois fatos a seguir:

• Na raiz da pilha, nem sempre há irmãos direitos e esquerdos.
• Se qualquer nó U tiver um ponteiro diferente de zero para o nó filho mais à esquerda, esse nó será o 'Head' da lista duplamente vinculada de todos os nós filhos de U. Essa lista é chamada siblingList.

A seguir, listamos o algoritmo das principais operações no Min Pairing-Heap :

• Inserir nó no Heap de emparelhamento:
  
  Seja dado um Heap de emparelhamento com uma raiz e um valor nele {R, V_1} , bem como um nó {U, V_2} . Em seguida, ao inserir um nó U em um determinado Heap de Emparelhamento:
  
  • Se a condição V_2 <V_1 for satisfeita: U se torna o novo nó raiz do heap, 'removendo' a raiz R para a posição do nó filho esquerdo. Ao mesmo tempo, o irmão direito do nó R se torna o nó mais à esquerda mais antigo e o ponteiro para o nó mais à esquerda do nó R se torna zero.
  • Caso contrário: U se torna o nó filho mais à esquerda da raiz de R e seu irmão mais velho é o nó mais à esquerda da raiz de R.
• Mesclando dois heap de emparelhamento:
  
  Permita que dois Heaps de emparelhamento com raízes e valores neles sejam {R_1, V_1} , {R_2, V_2}, respectivamente. Descrevemos um dos algoritmos para mesclar esses heaps no Heap de emparelhamento resultante:
  
  • Escolha a pilha com o menor valor na raiz. Que seja um monte de {R_1, V_1}.
  • 'Desconecte' a raiz R_1 da pilha selecionada: para isso, simplesmente anulamos seu ponteiro no nó filho mais à esquerda.
  • Com o novo ponteiro para o nó filho mais à esquerda da raiz R_1, crie a raiz R_2. Observe que a partir de agora, R_2 perde o status raiz e é um nó normal na pilha resultante.
  • Definimos o irmão direito do nó R_2: com o novo valor, tornamos o ponteiro antigo (antes de zerar) para o nó filho mais à esquerda da raiz R_1 e, para R_1, respectivamente, atualizamos o ponteiro para o irmão esquerdo.

Considere o algoritmo de mesclagem usando um exemplo específico:



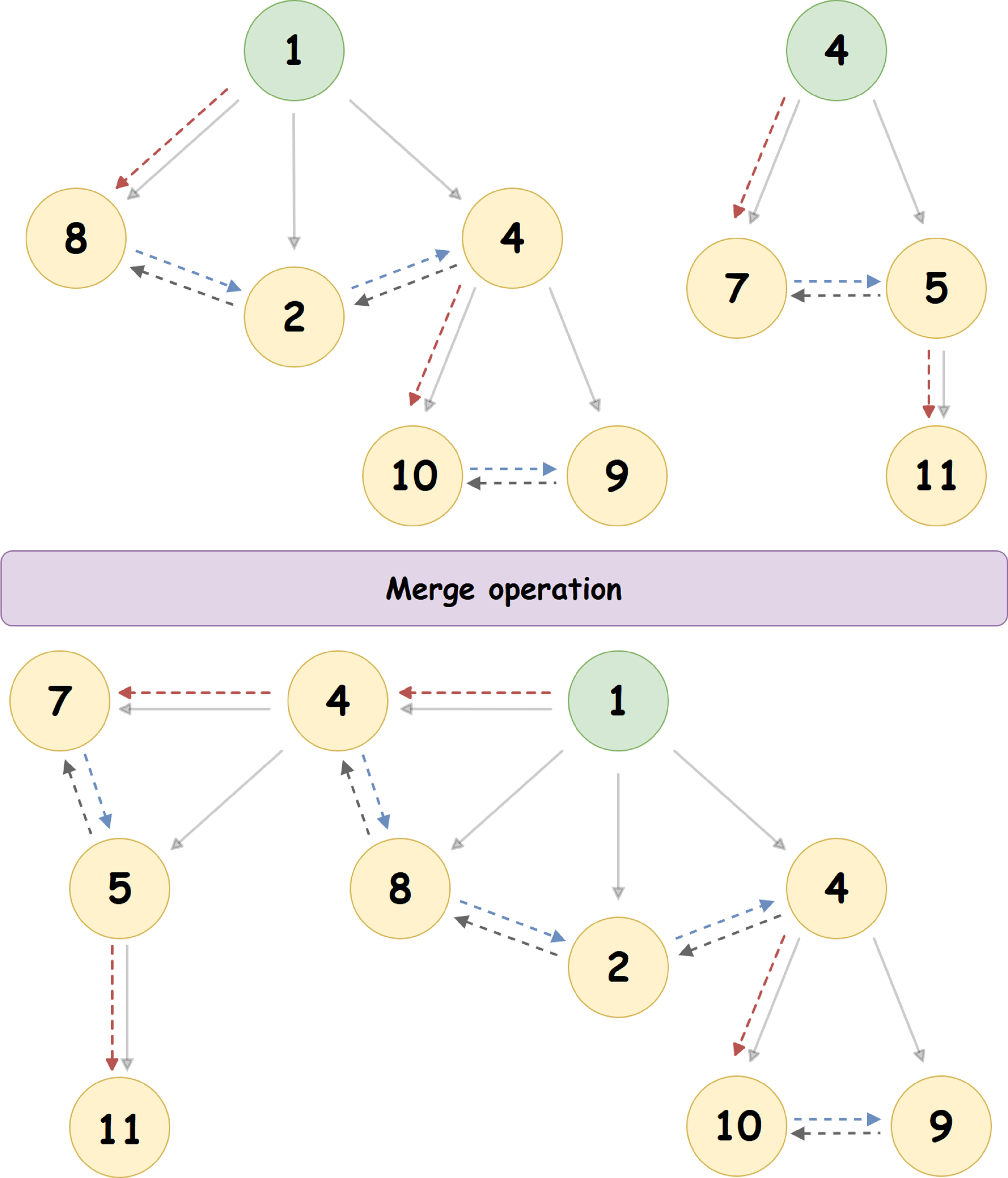Aqui, o heap com a raiz '4' une o heap com a raiz '1' (1 <4), tornando-se o nó filho mais à esquerda. O ponteiro para o irmão direito do nó '4' - é atualizado, bem como o ponteiro para o irmão esquerdo do nó '8'.

• Removendo a raiz (nó com o valor mínimo) Heap de emparelhamento:
  
  Existem vários algoritmos para remover um nó de um Heap de emparelhamento, que garantem uma estimativa amortizada da complexidade em O (log N). Nós descrevemos um deles, chamado algoritmo multipass e usado no JeMalloc:
  
  
  • Excluímos a raiz do heap fornecido, deixando apenas o nó filho mais à esquerda.
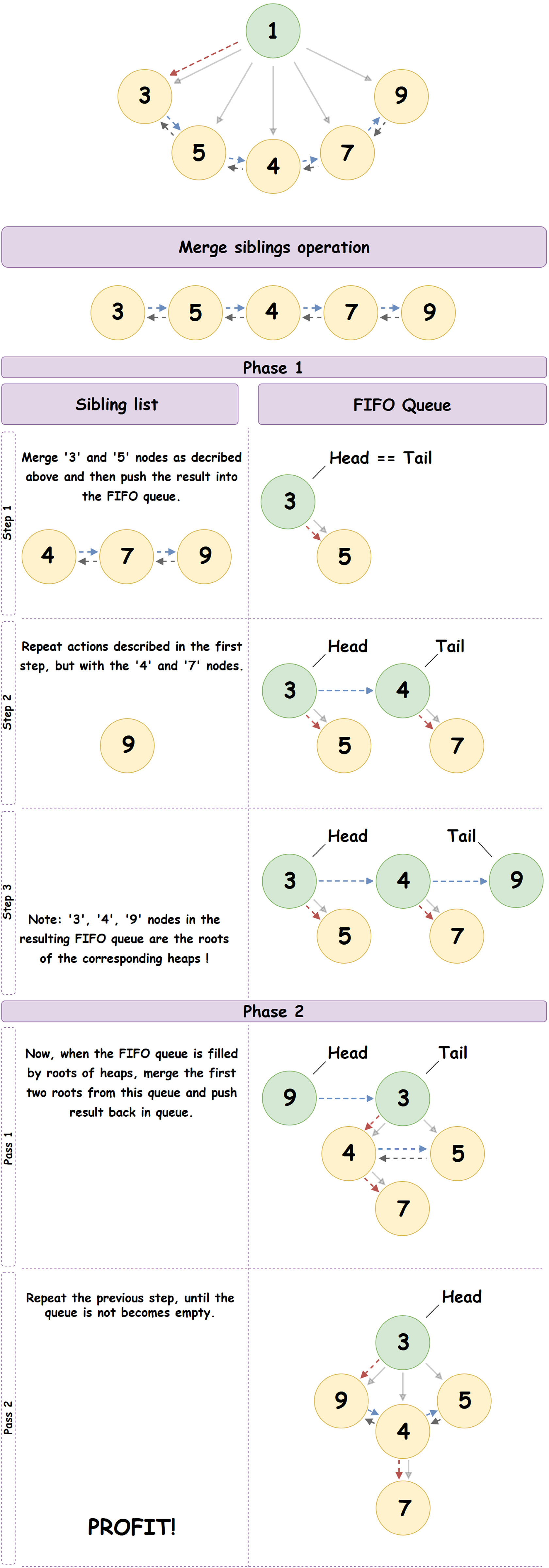
  • O nó filho mais à esquerda forma uma lista duplamente vinculada de todos os nós filhos do nó pai e, no nosso caso, a raiz excluída anteriormente. Iremos sequencialmente por essa lista até o final e, considerando os nós como raízes do Pairing Heap independente, executaremos a operação de mesclar o elemento atual da lista com o próximo, colocando o resultado em uma fila FIFO pré-preparada.
  • Agora que a fila FIFO foi inicializada, iremos iterar sobre ela, realizando a operação de mesclar o elemento atual da fila com o próximo. O resultado da fusão é colocado no final da fila.
  • Repetimos a etapa anterior até que um elemento permaneça na fila: a pilha de emparelhamento resultante.

Um bom exemplo do processo descrito acima:

• Removendo um nó não raiz arbitrário Pairing Heap:
  
  Considere o nó excluído como a raiz de alguma subárvore do Heap original. Primeiro, removemos a raiz dessa subárvore, seguindo o algoritmo descrito anteriormente para remover a raiz da pilha de emparelhamento e, em seguida, executamos o procedimento de mesclar a árvore resultante à original.
• Obtendo o elemento mínimo Heap de emparelhamento:
  
  Basta retornar o valor da raiz da pilha.

No entanto, nosso conhecimento do Pairing Heap não termina aí: O Pairing Heap permite executar algumas operações não imediatamente, mas somente quando houver necessidade delas. Em outras palavras, o Pairing Heap permite executar operações 'Preguiçosamente' , reduzindo assim o custo amortizado de algumas delas.
Suponha que fizemos inserções K e exclusões K no Heap de emparelhamento. Obviamente, o resultado dessas operações se torna necessário apenas quando solicitamos o elemento mínimo do heap.
Vamos considerar como o algoritmo de ações das operações descritas anteriormente será alterado durante a implementação do Lazy:

Aproveitando o fato de que a raiz Kuchi possui pelo menos dois ponteiros nulos, usaremos um deles para representar o cabeçalho de uma lista duplamente vinculada (doravante auxList ) de elementos inseridos no heap, cada um dos quais será considerado a raiz de um Heap de emparelhamento independente. Então:

• Inserção de nó lento no Heap de emparelhamento:
  
  Ao inserir o nó U especificado no Heap de emparelhamento { R_1 , V_1 }, o colocamos em auxList - após o cabeçalho da lista:

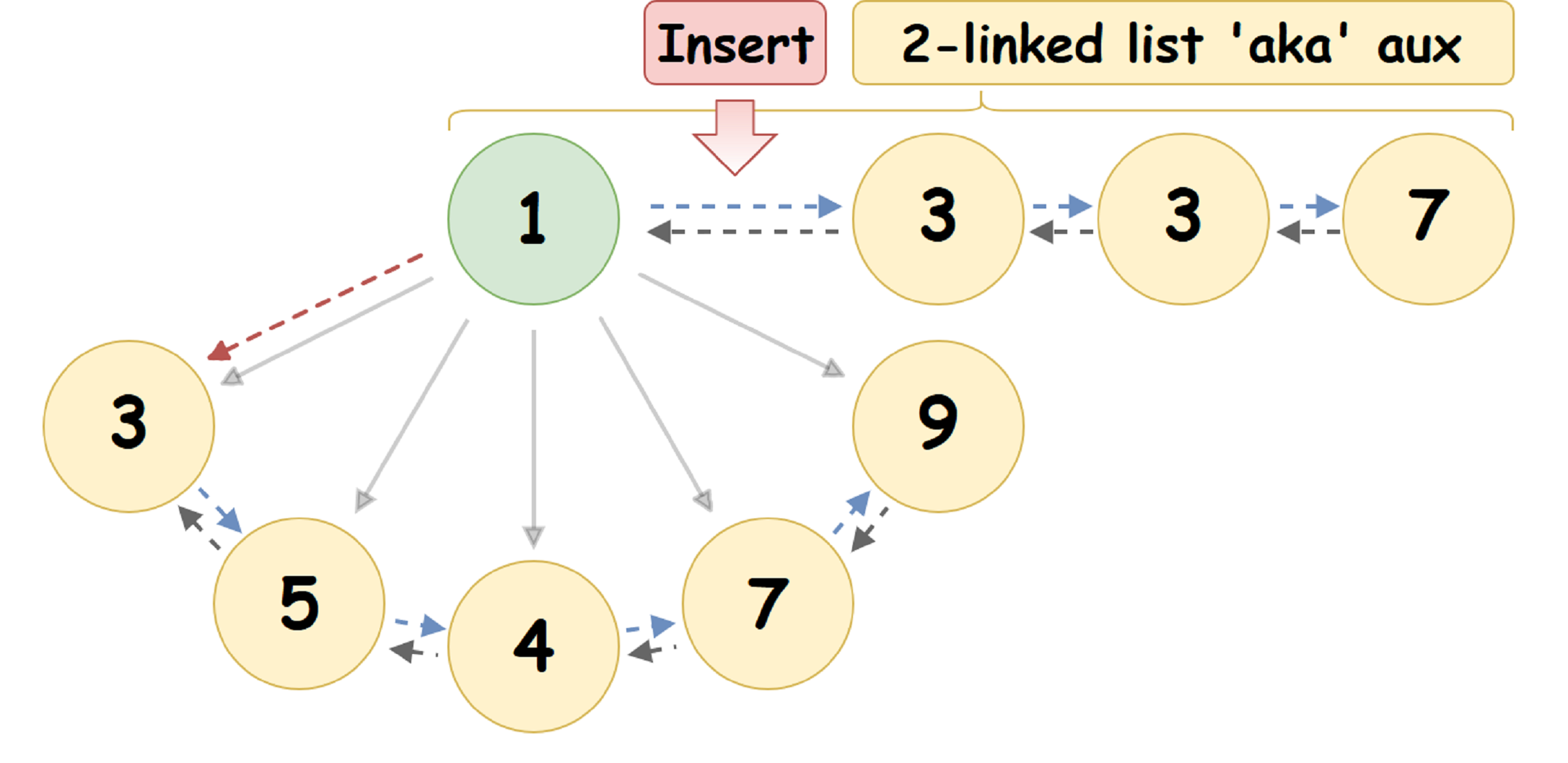
• A fusão lenta de dois heap de emparelhamento:
  
  Lazy Mesclando dois heap de emparelhamento, semelhante à inserção do nó Lazy, em que o nó inserido é a raiz (cabeça da auxList duplamente conectada) de um dos heaps.
• Preguiçoso, obtendo o elemento mínimo Heap de emparelhamento:
  
  Ao solicitar um mínimo, passamos por auxList à lista de raízes do Heap de emparelhamento independente, combinando em pares os elementos desta lista com a operação de mesclagem e retornamos o valor da raiz que contém o elemento mínimo a um dos Heap de emparelhamento resultante.
• Remoção lenta do elemento mínimo de Heap de emparelhamento:
  
  Ao solicitar a remoção do elemento mínimo especificado pelo Heap de Emparelhamento, primeiro encontramos o nó que contém o elemento mínimo e, em seguida, o removemos da árvore em que é a raiz, inserindo suas subárvores na auxList do heap principal.
• Remoção lenta de um nó de Heap de emparelhamento não raiz arbitrário:
  
  Ao excluir um nó de Heap de emparelhamento não raiz arbitrário, o nó é removido da pilha e seus nós filhos são inseridos na lista auxiliar do Heap principal.

Na verdade, o uso da implementação Lazy Pairing Heap reduz o custo amortizado de inserir e excluir nós arbitrários no Pairing Heap: de O (log N) a O (1).

É tudo, e abaixo você encontrará uma lista de links e recursos úteis:

[0] Página JeMalloc Github
[1] Artigo original sobre Emparelhamento de pilhas
[2] Artigo original no Lazy Implementation Pairing Heaps
[3] Canal de telegrama sobre otimizações de código, C ++, Asm, 'baixo nível' e nada mais do que isso!

Para continuar ...