Equação de Navier-Stokes e simulação de fluidos na CUDA

Oi Habr. Neste artigo, trataremos da equação de Navier-Stokes para um fluido incompressível, resolveremos numericamente e faremos uma bela simulação que funciona por computação paralela na CUDA. O objetivo principal é mostrar como você pode aplicar a matemática subjacente à equação na prática ao resolver o problema de modelagem de líquidos e gases.




Nota: se você estiver lendo o Habr em um dispositivo móvel e não vir as fórmulas, use a versão completa do site

Equação de Navier-Stokes para um fluido incompressível

$$

$${\ parcial {\ bf \ vec {u}} \ over {\ t parcial}} = - ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}} - {1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$$

Acho que todos pelo menos uma vez ouviram falar dessa equação, alguns, talvez até analiticamente, resolvam seus casos particulares, mas em termos gerais esse problema permanece por resolver até agora. Obviamente, não definimos o objetivo de resolver o problema do milênio neste artigo, mas ainda podemos aplicar o método iterativo a ele. Mas, para começar, vejamos a notação nesta fórmula.

Convencionalmente, a equação de Navier-Stokes pode ser dividida em cinco partes:

• $$$\ parcial {\ bf \ vec {u}} \ mais \ parcial t$ - denota a taxa de variação da velocidade do fluido em um ponto (a consideraremos para cada partícula em nossa simulação).
• $$$- ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}}$ - o movimento do fluido no espaço.
• $$$- {1 \ over \ rho} \ nabla {\ bf p}$ A pressão exercida sobre a partícula (aqui $$$\ rho$ - coeficiente de densidade do fluido).
• $$$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ - viscosidade do meio (quanto maior, mais forte o líquido resiste à força aplicada à sua parte), $$$\ nu$ - coeficiente de viscosidade).
• $$$\ bf \ vec {F}$ - forças externas que aplicamos ao fluido (no nosso caso, a força terá um papel muito específico - refletirá as ações executadas pelo usuário.

Além disso, como consideraremos o caso de um fluido incompressível e homogêneo, temos outra equação: $$${{\ \ nabla \ cdot \ bf \ vec {u}} = 0}$ . A energia no ambiente é constante, não vai a lugar nenhum, não vem de nenhum lugar.

Será errado privar todos os leitores que não estão familiarizados com a análise vetorial , portanto, ao mesmo tempo, e passar brevemente por todos os operadores presentes na equação (no entanto, eu recomendo fortemente lembrar qual é a derivada, o diferencial e o vetor, pois eles sustentam tudo isso. o que será discutido abaixo).

Começamos com o operador nabla, que é esse vetor (no nosso caso, será de dois componentes, pois modelaremos o fluido no espaço bidimensional):

$$

$$\ nabla = {\ begin {pmatrix} {\ parcial \ sob \ parcial x}, {\ parcial \ sobre \ parcial y} \ end {pmatrix}}$$

O operador nabla é um operador diferencial de vetor e pode ser aplicado tanto a uma função escalar quanto a uma função vetorial. No caso de um escalar, obtemos o gradiente da função (o vetor de suas derivadas parciais) e, no caso de um vetor, a soma das derivadas parciais ao longo dos eixos. A principal característica desse operador é que, através dele, você pode expressar as principais operações da análise vetorial - grad ( gradiente ), div ( divergência ), rot ( rotor ) e $$$\ nabla ^ 2$ ( Operador Laplace ). Vale a pena notar imediatamente que a expressão $$$({\ bf \ vec {u} \ cdot \ nabla}) {\ bf \ vec {u}}$ não equivale a $$$({\ nabla \ cdot \ bf \ vec {u}}) {\ bf \ vec {u}}$ - o operador nabla não possui comutatividade.

Como veremos mais adiante, essas expressões são visivelmente simplificadas ao mudar para um espaço discreto no qual realizaremos todos os cálculos; portanto, não fique alarmado se no momento você não estiver muito claro sobre o que fazer com tudo isso. Depois de dividir a tarefa em várias partes, resolveremos sucessivamente cada uma delas e apresentaremos tudo isso na forma da aplicação seqüencial de várias funções em nosso ambiente.

Solução numérica da equação de Navier-Stokes

Para representar nosso fluido no programa, precisamos obter uma representação matemática do estado de cada partícula de fluido em um ponto arbitrário no tempo. O método mais conveniente para isso é criar um campo vetorial de partículas armazenando seu estado na forma de um plano de coordenadas:



Em cada célula da nossa matriz bidimensional, armazenaremos a velocidade das partículas por vez $$$t: {\ bf \ vec {u}} = u ({\ bf \ vec {x}}, t), \ bf \ vec {x} = \ begin {pmatrix} x, y \ end {pmatrix}$ , e a distância entre as partículas é indicada por $$$\ delta x$ e $$$\ delta y$ em conformidade. No código, será suficiente alterar o valor da velocidade a cada iteração, resolvendo um conjunto de várias equações.

Agora, expressamos o gradiente, a divergência e o operador Laplace, levando em consideração nossa grade de coordenadas ( $$$i, j$ - índices na matriz, $$$\ bf \ vec {u} _ {(x)}, \ vec {u} _ {(y)}$ - retirando os componentes correspondentes do vetor):

Podemos simplificar ainda mais as fórmulas discretas dos operadores de vetores se assumirmos que $$$\ delta x = \ delta y = 1$ . Essa suposição não afetará muito a precisão do algoritmo, no entanto, reduz o número de operações por iteração e geralmente torna as expressões mais agradáveis ​​aos olhos.

Movimento de partículas

Essas declarações funcionam apenas se pudermos encontrar as partículas mais próximas em relação à que está sendo considerada no momento. Para anular todos os custos possíveis associados à sua localização, rastrearemos não o movimento deles, mas de onde as partículas vêm no início da iteração, projetando a trajetória do movimento para trás no tempo (em outras palavras, subtraia o vetor de velocidade vezes a mudança de tempo de posição atual). Usando esta técnica para cada elemento da matriz, teremos certeza de que qualquer partícula terá "vizinhos":



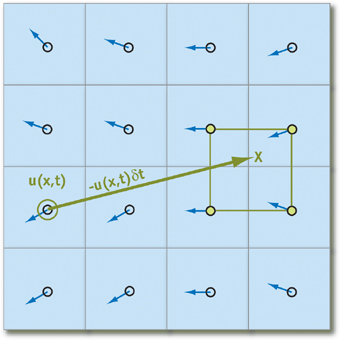
Colocando isso $$$q$ - um elemento da matriz que armazena o estado da partícula, obtemos a seguinte fórmula para calcular seu estado ao longo do tempo $$$\ delta t$ (acreditamos que todos os parâmetros necessários na forma de aceleração e pressão já foram calculados):

$$

$$q ({{\ \ vec {\ bf x}}, t + \ delta t}) = q ({{\ \ bf \ vec {x}} - {\ bf \ vec {u}} \ delta t}, t)$$

Notamos imediatamente que, para pequenas quantidades $$$\ delta t$ e nunca podemos ir além dos limites da célula, portanto, é muito importante escolher o momento certo que o usuário dará às partículas.

Para evitar a perda de precisão no caso de uma projeção no limite da célula ou no caso de coordenadas não inteiras, realizaremos a interpolação bilinear dos estados das quatro partículas mais próximas e a consideraremos como o valor verdadeiro em um ponto. Em princípio, esse método praticamente não reduz a precisão da simulação e, ao mesmo tempo, é bastante simples de implementar, por isso vamos usá-lo.

Viscosidade

Cada líquido tem uma certa viscosidade, a capacidade de impedir a influência de forças externas em suas partes (mel e água serão um bom exemplo, em alguns casos, seus coeficientes de viscosidade diferem em uma ordem de magnitude). A viscosidade afeta diretamente a aceleração adquirida pelo líquido e pode ser expressa pela fórmula abaixo, se, por questões de brevidade, omitirmos outros termos por um tempo:

$$

$${\ parcial \ vec {\ bf u} \ sobre \ parcial t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$$

. Nesse caso, a equação iterativa para velocidade assume a seguinte forma:

$$

$$u ({\ bf \ vec {x}}, t + \ delta t) = u ({\ bf \ vec {x}}, t) + \ nu \ delta t \ nabla ^ 2 \ bf \ vec {u }$$

Transformaremos levemente essa igualdade, trazendo-a para a forma $$$\ bf A \ vec {x} = \ vec {b}$ (forma padrão de um sistema de equações lineares):

$$

$$({\ bf I} - \ nu \ delta t \ nabla ^ 2) u ({\ bf \ vec {x}}, t + \ delta t) = {u ({\ bf \ vec {x}}, t )}$$

onde $$$\ bf I$ É a matriz de identidade. Precisamos dessas transformações para posteriormente aplicar o método de Jacobi para resolver vários sistemas de equações semelhantes. Também discutiremos isso mais tarde.

Forças externas

O passo mais simples do algoritmo é a aplicação de forças externas ao meio. Para o usuário, isso será refletido na forma de cliques na tela com o mouse ou seu movimento. A força externa pode ser descrita pela fórmula a seguir, que aplicamos a cada elemento da matriz ( $$$\ vec {\ bf G}$ - vetor de momento $$$x_p, y_p$ - posição do mouse $$$x, y$ - coordenadas da célula atual, $$$r$ - raio de ação, parâmetro de escala):

$$

$$\ vec {\ bf F} = \ vec {\ bf G} \ delta t {\ bf exp} \ left (- {{(x - x_p) ^ 2 + (y - y_p) ^ 2} \ sobre r} \ right)$$

Um vetor de impulso pode ser facilmente calculado como a diferença entre a posição anterior do mouse e a atual (se houver), e aqui você ainda pode ser criativo. É nesta parte do algoritmo que podemos introduzir a adição de cores a um líquido, sua iluminação etc. As forças externas também podem incluir gravidade e temperatura e, embora não seja difícil implementar tais parâmetros, não os consideraremos neste artigo.

Pressão

A pressão na equação de Navier-Stokes é a força que impede que as partículas preencham todo o espaço disponível após aplicar qualquer força externa nelas. Imediatamente, seu cálculo é muito difícil, mas nosso problema pode ser bastante simplificado aplicando o teorema da decomposição de Helmholtz .

Ligar $$$\ bf \ vec {W}$ campo vetorial obtido após o cálculo do deslocamento, forças externas e viscosidade. Apresentará uma divergência diferente de zero, o que contradiz a condição de incompressibilidade do líquido ( $$$\ nabla \ cdot \ bf \ vec {u} = 0$ ) e, para corrigir isso, é necessário calcular a pressão. De acordo com o teorema da decomposição de Helmholtz, $$$\ bf \ vec {W}$ pode ser representado como a soma de dois campos:

$$

$$\ bf \ vec {W} = \ vec {u} + \ na p$$

onde $$$\ bf u$ - este é o campo vetorial que procuramos com divergência zero. Nenhuma prova dessa igualdade será fornecida neste artigo, mas no final você pode encontrar um link com uma explicação detalhada. Podemos aplicar o operador nabla nos dois lados da expressão para obter a seguinte fórmula para calcular o campo de pressão escalar:

$$

$$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot (\ vec {u} + \ nabla p) = \ nabla \ cdot \ vec {u} + \ nabla ^ 2 p = \ nabla ^ 2 p$$

A expressão escrita acima é a equação de Poisson para pressão. Também podemos resolvê-lo pelo método de Jacobi acima mencionado e, assim, encontrar a última variável desconhecida na equação de Navier-Stokes. Em princípio, os sistemas de equações lineares podem ser resolvidos de várias maneiras diferentes e sofisticadas, mas ainda vamos nos concentrar nas mais simples delas, para não sobrecarregar ainda mais este artigo.

Limite e condições iniciais

Qualquer equação diferencial modelada em um domínio finito requer condições iniciais ou de contorno especificadas corretamente, caso contrário, é muito provável que obtenhamos um resultado fisicamente incorreto. As condições de contorno são estabelecidas para controlar o comportamento do fluido próximo às bordas da grade de coordenadas, e as condições iniciais especificam os parâmetros que as partículas têm no momento em que o programa é iniciado.

As condições iniciais serão muito simples - inicialmente o fluido é estacionário (a velocidade das partículas é zero) e a pressão também é zero. As condições de contorno serão definidas para velocidade e pressão pelas fórmulas fornecidas:

$$

$${\ bf \ vec {u} _ {0, j} + \ bf \ vec {u} _ {1, j} \ mais de 2 \ delta y} = 0, {\ bf \ vec {u} _ {i , 0} + \ bf \ vec {u} _ {i, 1} \ mais de 2 \ delta x} = 0$$

$$

$${\ bf p_ {0, j} - \ bf p_ {1, j} \ over \ delta x} = 0, {\ bf p_ {i, 0} - \ bf p_ {i, 1} \ over \ delta y} = 0$$

Assim, a velocidade das partículas nas bordas será oposta à velocidade nas bordas (assim elas se repelirão a partir da borda), e a pressão é igual ao valor imediatamente próximo ao limite. Essas operações devem ser aplicadas a todos os elementos delimitadores da matriz (por exemplo, há um tamanho de grade $$$N \ vezes M$ , aplicamos o algoritmo às células marcadas em azul na figura):

Corante

Com o que temos agora, você já pode ter muitas coisas interessantes. Por exemplo, para perceber a propagação do corante em um líquido. Para fazer isso, precisamos apenas manter outro campo escalar, que seria responsável pela quantidade de tinta em cada ponto da simulação. A fórmula para atualizar o corante é muito semelhante à velocidade e é expressa como:

$$

$${\ parcial d \ sobre \ parcial t} = {- (\ vec {\ bf u} \ cdot \ nabla) d} + \ gama \ nabla ^ 2d + S$$

Na fórmula $$$S$ responsável por reabastecer a área com um corante (possivelmente dependendo de onde o usuário clica), $$$d$ diretamente é a quantidade de corante no ponto e $$$\ gama$ - coeficiente de difusão. Não é difícil resolvê-lo, pois todo o trabalho básico sobre derivação de fórmulas já foi realizado e basta fazer algumas substituições. A tinta pode ser implementada no código como uma cor no formato RGB e, nesse caso, a tarefa é reduzida a operações com vários valores reais.

Vorticidade

A equação de vorticidade não é uma parte direta da equação de Navier-Stokes, mas é um parâmetro importante para uma simulação plausível do movimento de um corante em um líquido. Devido ao fato de estarmos produzindo um algoritmo em um campo discreto, bem como devido a perdas na precisão dos valores de ponto flutuante, esse efeito é perdido e, portanto, precisamos restaurá-lo aplicando força adicional a cada ponto no espaço. O vetor dessa força é designado como $$$\ bf \ vec {T}$ e é determinado pelas seguintes fórmulas:

$$

$$\ bf \ omega = \ nabla \ times \ vec {u}$$

$$

$$\ vec {\ eta} = \ nabla | \ omega |$$

$$

$$\ bf \ vec {\ psi} = {\ vec {\ eta} \ sobre {| \ vec {\ eta} |}}$$

$$

$$\ bf \ vec {T} = \ epsilon (\ vec {\ psi} \ times \ omega) \ delta x$$

$$$\ omega$ há o resultado da aplicação do rotor ao vetor de velocidade (sua definição é dada no início do artigo), $$$\ vec \ eta$ - gradiente do campo escalar de valores absolutos $$$\ omega$ . $$$\ vec \ psi$ representa um vetor normalizado $$$\ vec \ eta$ e $$$\ epsilon$ É uma constante que controla o tamanho dos vórtices em nosso fluido.

Método de Jacobi para resolver sistemas de equações lineares

Ao analisar as equações de Navier-Stokes, criamos dois sistemas de equações - um para viscosidade e outro para pressão. Eles podem ser resolvidos por um algoritmo iterativo, que pode ser descrito pela seguinte fórmula iterativa:

$$

$$x ^ {(k + 1)} _ {i, j} = {{x ^ {(k)} _ {i-1, j} + x ^ {(k)} _ {i + 1, j} + x ^ {(k)} _ {i, j-1} + x ^ {(k)} _ {i, j + 1} + \ alpha b_ {i, j}} \ over \ beta}$$

Para nós $$$x$ - elementos de matriz que representam um campo escalar ou vetorial. $$$k$ - o número da iteração, podemos ajustá-lo para aumentar a precisão do cálculo ou vice-versa para reduzi-lo e aumentar a produtividade.

Para calcular a viscosidade, substituímos: $$$x = b = \ bf \ vec {u}$ , $$$\ alpha = {1 \ over \ nu \ delta t}$ , $$$\ beta = 4+ \ alpha$ , aqui está o parâmetro $$$\ beta$ - a soma dos pesos. Portanto, precisamos armazenar pelo menos dois campos de velocidade vetorial para ler independentemente os valores de um campo e gravá-los em outro. Em média, para calcular o campo de velocidade pelo método Jacobi, é necessário realizar de 20 a 50 iterações, o que é bastante se realizarmos cálculos na CPU.

Para a equação da pressão, fazemos a seguinte substituição: $$$x = p$ , $$$b = \ nabla \ bf \ cdot \ vec {W}$ , $$$\ alpha = -1$ , $$$\ beta = 4$ . Como resultado, obtemos o valor $$$p_ {i, j} \ delta t$ no ponto. Porém, como é usado apenas para calcular o gradiente subtraído do campo de velocidade, transformações adicionais podem ser omitidas. Para o campo de pressão, é melhor executar iterações de 40 a 80, porque com números menores a discrepância se torna perceptível.

Implementação de algoritmo

Vamos implementar o algoritmo em C ++, também precisamos do Cuda Toolkit (você pode ler como instalá-lo no site da Nvidia), bem como do SFML . Precisamos que o CUDA paralelize o algoritmo, e o SFML será usado apenas para criar uma janela e exibir uma imagem na tela (em princípio, isso pode ser escrito em OpenGL, mas a diferença de desempenho não será significativa, mas o código aumentará em mais de 200 linhas).

Cuda toolkit

Primeiro, falaremos um pouco sobre como usar o Cuda Toolkit para paralelizar tarefas. Um guia mais detalhado é fornecido pela própria Nvidia; portanto, aqui nos restringimos apenas ao mais necessário. Supõe-se também que você conseguiu instalar o compilador e conseguiu criar um projeto de teste sem erros.

Para criar uma função que é executada na GPU, primeiro você precisa declarar quantos kernels queremos usar e quantos blocos de kernels precisamos alocar. Para isso, o Cuda Toolkit nos fornece uma estrutura especial - dim3 , por padrão, configurando todos os seus valores de x, y, z como 1. Ao especificá-lo como argumento ao chamar a função, podemos controlar o número de kernels alocados. Como estamos trabalhando com uma matriz bidimensional, precisamos definir apenas dois campos no construtor: xey :

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads); 

onde size_x e size_y são o tamanho da matriz que está sendo processada. A assinatura e a chamada de função são as seguintes (colchetes de ângulo triplo são processados ​​pelo compilador Cuda):

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host 

Na própria função, você pode restaurar os índices de uma matriz bidimensional através do número do bloco e do número do kernel nesse bloco, usando a seguinte fórmula:

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; 

Deve-se observar que a função executada na placa de vídeo deve ser marcada com a tag __global__ e também retornar nula , portanto, na maioria das vezes, os resultados do cálculo são gravados na matriz passada como argumento e pré-alocada na memória da placa de vídeo.

As funções CudaMalloc e CudaFree são responsáveis ​​por liberar e alocar memória na placa de vídeo. Podemos operar ponteiros para a área de memória que eles retornam, mas não podemos acessar os dados do código principal. A maneira mais fácil de retornar os resultados do cálculo é usar cudaMemcpy , semelhante ao memcpy padrão, mas capaz de copiar dados de uma placa de vídeo para a memória principal e vice-versa.

SFML e renderização de janela

Armado com todo esse conhecimento, podemos finalmente começar a escrever código diretamente. Para começar, vamos criar o arquivo main.cpp e colocar todo o código auxiliar para a janela renderizada lá:


linha no início da função principal

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); 

cria uma imagem RGBA na forma de uma matriz unidimensional com um comprimento constante. Passaremos junto com outros parâmetros (posição do mouse, diferença entre os quadros) para a função computeField . As últimas, assim como várias outras funções, são declaradas no kernel.cu e chamam o código executado na GPU. Você pode encontrar documentação sobre qualquer uma das funções no site da SFML, nada super interessante está acontecendo no código do arquivo, por isso não vamos parar por muito tempo.

Computação GPU

Para começar a escrever código no gpu, primeiro crie um arquivo kernel.cu e defina várias classes auxiliares: Color3f, Vec2, Config, SystemConfig :


O atributo __host__ na frente do nome do método significa que o código pode ser executado na CPU; __dispositivo__ , pelo contrário, obriga o compilador a coletar código na GPU. O código declara primitivas para trabalhar com vetores de dois componentes, cor, configurações com parâmetros que podem ser alterados em tempo de execução, além de vários ponteiros estáticos para matrizes, que usaremos como buffers para cálculos.

cudaInit e cudaExit também são definidos de maneira bastante trivial:


Na função de inicialização, alocamos memória para matrizes bidimensionais, especificamos uma matriz de cores que usaremos para pintar o líquido e também definimos os valores padrão na configuração. Em cudaExit, apenas liberamos todos os buffers. Por mais paradoxal que pareça, para armazenar matrizes bidimensionais, é mais vantajoso usar matrizes unidimensionais, cujo acesso será realizado com a seguinte expressão:

 array[y * size_x + x]; // equals to array[y][x] 

Iniciamos a implementação do algoritmo direto com a função de deslocamento de partículas. Os campos oldField e newField (o campo de onde os dados vêm e para onde são gravados), o tamanho da matriz, bem como o delta de tempo e o coeficiente de densidade (usado para acelerar a dissolução do corante no líquido e tornar o meio não muito sensível a ações do usuário). A função de interpolação bilinear é implementada de maneira clássica, calculando valores intermediários:


Decidiu-se dividir a função de difusão da viscosidade em várias partes: computeDiffusion é chamada a partir do código principal, que chama difusa e computeColor um número predeterminado de vezes e depois troca a matriz de onde pegamos os dados e a onde os escrevemos. Essa é a maneira mais fácil de implementar o processamento de dados paralelos, mas estamos gastando o dobro de memória.

Ambas as funções causam variações do método Jacobi. O corpo de jacobiColor e jacobiVelocity verifica imediatamente se os elementos atuais não estão na borda - nesse caso, devemos defini-los de acordo com as fórmulas descritas na seção Limite e condições iniciais .


O uso da força externa é implementado através de uma única função - applyForce , que leva como argumento a posição do mouse, a cor do corante e também o raio de ação. Com sua ajuda, podemos dar velocidade às partículas e pintá-las. O expoente fraterno permite que você deixe a área não muito nítida e, ao mesmo tempo, bastante clara no raio especificado.


O cálculo da vorticidade já é um processo mais complicado, portanto, implementado em computateVorticity e applyVorticity , também observamos que para eles é necessário definir dois operadores vetoriais como curl (rotor) e absGradient (gradiente de valores absolutos de campo). Para especificar efeitos de vórtice adicionais, multiplicamos $$$y$ componente do vetor gradiente em $$$-1$ e normalize-o dividindo pelo comprimento (sem esquecer de verificar se o vetor é diferente de zero):


O próximo passo no algoritmo será o cálculo do campo de pressão escalar e sua projeção no campo de velocidade. Para fazer isso, precisamos implementar 4 funções: divergência , que considerará a divergência de velocidade, jacobiPressure , que implementa o método Jacobi para pressão, e compututePressure com computePressureImpl , executando cálculos de campo iterativos:


A projeção se encaixa em duas pequenas funções - projeto e o gradiente que exige pressão. Pode-se dizer o último estágio do nosso algoritmo de simulação:


Após a projeção, podemos proceder com segurança para renderizar a imagem no buffer e em vários pós-efeitos. A função de pintura copia cores do campo de partículas para a matriz RGBA. A função applyBloom também foi implementada, que destaca o líquido quando o cursor é colocado nele e o botão do mouse é pressionado. Por experiência, essa técnica torna a imagem mais agradável e interessante para os olhos do usuário, mas não é necessária.

No pós-processamento, você também pode destacar locais onde o fluido tem a velocidade mais alta, mudar de cor dependendo do vetor de movimento, adicionar vários efeitos etc., mas, no nosso caso, nos limitaremos a um mínimo, porque mesmo com isso as imagens são muito fascinantes (especialmente em dinâmica) :


E no final, ainda temos uma função principal que chamamos de main.cpp - computeField . Ele liga todas as partes do algoritmo, chamando o código na placa de vídeo, e também copia os dados de gpu para cpu. Ele também contém o cálculo do vetor de momento e a escolha da cor do corante, que passamos a aplicar a força :

Conclusão

Neste artigo, analisamos um algoritmo numérico para resolver a equação de Navier-Stokes e escrevemos um pequeno programa de simulação para um fluido incompressível. Talvez não tenhamos entendido todos os meandros, mas espero que o material tenha sido interessante e útil para você, e pelo menos tenha servido como uma boa introdução ao campo da modelagem de fluidos.

Como autor deste artigo, sinceramente aprecio quaisquer comentários e adições e tentarei responder a todas as suas perguntas neste post.

Material adicional

Você pode encontrar todo o código-fonte neste artigo no meu repositório do Github . Todas as sugestões de melhoria são bem-vindas.

O material original que serviu de base para este artigo, você pode ler no site oficial da Nvidia. Também apresenta exemplos da implementação de partes do algoritmo na linguagem dos shaders:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

A prova do teorema da decomposição de Helmholtz e uma enorme quantidade de material adicional sobre mecânica dos fluidos podem ser encontradas neste livro (em inglês, consulte a seção 1.2):
Chorin, AJ e JE Marsden. 1993. Uma Introdução Matemática à Mecânica dos Fluidos. 3rd ed. Springer

Canal de um YouTube de língua inglesa, criando conteúdo de qualidade relacionado à matemática e resolvendo equações diferenciais em particular (inglês). Vídeos muito visuais que ajudam a entender a essência de muitas coisas em matemática e física:
3Blue1Brown -
Equações diferenciais do YouTube (3Blue1Brown)

Também agradeço ao WhiteBlackGoose pela ajuda na preparação do material para o artigo.

---

E, no final, um pequeno bônus - algumas belas capturas de tela tiradas no programa:


Stream direto (configurações padrão)


Whirlpool (grande raio no applyForce)


Wave (alta vorticidade + difusão)

Além disso, pela demanda popular, adicionei um vídeo com a simulação: