Oi, habrozhiteli! Recentemente, entregamos o
livro de Chris Bernhard,
Quantum Computing for Real IT . Aqui eles decidiram compartilhar um trecho do livro "Algoritmo de Grover e pesquisa de dados"
Estamos entrando na era do big data. Pesquisando conjuntos de dados gigantescos com eficiência é atualmente uma grande preocupação para muitas grandes empresas. O algoritmo de Grover é teoricamente capaz de acelerar a recuperação de dados.
Love Grover inventou seu algoritmo em 1996. Como os algoritmos de Deutsch e Simon, ele tem uma velocidade de execução mais alta em comparação aos algoritmos clássicos em termos de complexidade de consultas. No entanto, não conseguiremos implementar o algoritmo atual de recuperação de dados sem oráculos que possam fazer suas perguntas. Nós devemos construir um algoritmo que execute o trabalho do oráculo. Mas antes de começarmos a falar sobre a implementação do algoritmo Grover, vamos ver o que ele faz e como.
Algoritmo de Grover
Imagine que você tem quatro cartas de jogar. Eles estão de cabeça para baixo. Você sabe que um deles é um ás de vermes e precisa encontrá-lo. Quantas cartas você terá que jogar até saber onde está o ás de vermes?
Se você tiver sorte, encontrará a carta desejada na primeira tentativa; se não tiver sorte, poderá jogar três cartas e nenhuma delas será um ás de vermes. Na pior das hipóteses, ao virar três cartas, você terá certeza de que a última carta é o ás de worm que você está procurando. Assim, podemos descobrir onde está o ás, passando de uma a três cartas. Em média, você precisa virar 2,25 cartões.
Essa é uma das tarefas que o algoritmo de Grover resolve. Antes de iniciar a descrição do algoritmo, reformulamos o problema. Temos quatro seqüências binárias: 00, 01, 10 e 11. Temos uma função f que retorna 0 para três dessas sequências e 1 para a quarta sequência. Precisamos encontrar a sequência binária correspondente ao valor de saída 1. Por exemplo, podemos obter os seguintes resultados: f (00) = 0, f (01) = 0, f (10) = 1 ef (11) = 0. Agora, o problema é é descobrir quantas vezes a função deve ser calculada para obter o resultado f (10) = 1. Aqui, simplesmente reformulamos o problema substituindo as cartas de baralho por funções, de modo que a resposta a esta pergunta já é conhecida: como antes, em média, será necessário calcular a função 2,25 vezes.
Como em todos os algoritmos de consulta de complexidade, construímos um oráculo - um portão que encapsula uma função. O oráculo do nosso exemplo, onde existem apenas quatro seqüências binárias, é mostrado na Fig. 9.1
A cadeia para o algoritmo de Grover é mostrada na Fig. 9.2
O algoritmo executa duas etapas. No primeiro, o sinal da amplitude de probabilidade é invertido, associado ao local que estamos tentando encontrar. O segundo reforça essa amplitude de probabilidade. Vamos ver como a cadeia faz isso.
Após a transmissão pelas válvulas Hadamard, os dois qubits superiores obtêm o estado
e o qubit mais baixo tem um estado
O estado combinado pode ser escrito como
Os qubits passam pelo portão F. Inverte 0 e 1 no terceiro qubit para o local que estamos tentando encontrar. Para o nosso caso, f (10) = 1, obtemos
Pode ser reescrito como
Como resultado, obtemos dois qubits superiores, não confundidos com os inferiores, mas a amplitude de probabilidade
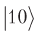
mudará o sinal, indicando o local desejado.
Se medirmos os dois qubits superiores nesta etapa, obtemos um dos quatro locais e todas as quatro respostas possíveis são igualmente prováveis. Precisamos dar outro passo - para aumentar a amplitude da probabilidade. A amplificação é realizada revertendo a sequência de números em relação à sua média. Se o número estiver acima da média, ele vira e fica abaixo da média. Se o número estiver abaixo da média, ele vira e fica acima da média. Em cada caso, o afastamento da média é mantido. Para ilustrar, usamos quatro números: 1, 1, 1 e –1. A soma deles é 2 e a média é 2/4 ou 1/2. Então começamos a classificar os números na sequência. O primeiro número é 1. É 1/2 acima da média. Após o golpe, ele deve ser 1/2 abaixo da média. Nesse caso, ele passará para 0. O número -1 está abaixo da média em 3/2. Após o golpe, ele deve ficar 3/2 acima da média, ou seja, se transformar em 2.
Atualmente, dois qubits superiores têm um estado
Girando as amplitudes em relação à média, obtemos

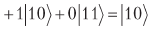
.
Depois de concluir a medição, obteremos definitivamente 10, ou seja, uma revolução sobre a média nos dá exatamente o que precisamos. Tudo o que precisamos fazer é garantir que haja um portão ou, o que é a mesma coisa, uma matriz ortogonal que descreve uma revolução em relação à média. Essa matriz existe:
Como resultado da ação da válvula nos dois qubits superiores, obtemos
Neste exemplo, onde temos apenas dois qubits, devemos usar o oráculo apenas uma vez. Basta que façamos a única pergunta. Para o caso n = 2, o algoritmo de Grover fornece uma resposta exata após uma única pergunta, enquanto que no caso clássico, em média, 2,25 perguntas precisam ser feitas.
Essa idéia se estende ao caso de um número arbitrário de n qubits. Começamos girando o sinal da amplitude de probabilidade, que corresponde ao local desejado. Então realizamos uma revolução em relação à média. No entanto, neste caso, a amplificação da amplitude não ocorre tão significativamente quanto na situação com dois qubits. Tomemos, por exemplo, oito números, sete dos quais são 1 e um é -1. A soma deles é 6 e a média é 6/8. Após um giro, a média 1 gira 1/2 e –1 gira 10/4. Como resultado, na presença de três qubits, medindo um qubit após amplificação da amplitude, obteremos o local desejado com uma probabilidade mais alta do que outros. O problema é que há uma chance significativa de obter a resposta errada. Precisamos de uma maior probabilidade de obter a resposta certa - precisamos ampliar ainda mais a amplitude antes de medir. A solução é transferir todos os qubits de volta pela cadeia. Mais uma vez, invertemos o sinal da amplitude de probabilidade associada ao local desejado e invertemos novamente em relação à média.
Considere o caso generalizado. Precisamos encontrar algo em um dos m locais possíveis. Para encontrá-lo da maneira clássica, no pior dos casos, temos que fazer m-1 perguntas. O número de perguntas cresce proporcionalmente a m. Grover calculou uma fórmula que determina quantas vezes sua cadeia precisa ser usada para obter a probabilidade máxima de uma resposta correta. O número que essa fórmula fornece aumenta proporcionalmente
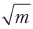
. Isso é aceleração quadrática.
Aplicações de algoritmo de Grover
Existem vários problemas com a implementação do algoritmo. Primeiro, a aceleração quadrática é avaliada em relação à solicitação de complexidade. Para usar o oracle, é necessário criá-lo e, se você não executar esta tarefa com o devido cuidado, o número de etapas executadas pelo oracle superará o número de etapas que o algoritmo salva e, como resultado, o algoritmo se tornará mais lento do que o clássico. Outro problema é que, ao determinar a aceleração, assumimos que o conjunto de dados está desordenado. Se o conjunto de dados tiver uma estrutura específica, você poderá encontrar frequentemente um algoritmo clássico que usa essa estrutura e procura uma solução muito mais rapidamente. O último problema está relacionado à aceleração. A aceleração quadrática nada mais é do que aceleração exponencial, que observamos em outros algoritmos. É possível conseguir mais? Vamos olhar para estas questões.
Ambos os problemas associados à implementação do oráculo e a presença da estrutura no conjunto de dados são justificados e mostram que, na maioria dos casos, o algoritmo de Grover não possui aplicação prática para pesquisar no banco de dados. Mas, em algumas situações, ter uma estrutura nos dados possibilita a criação de um oráculo que atua com alta eficiência. Em tais situações, o algoritmo pode ultrapassar algoritmos clássicos. A resposta para a questão da possibilidade de alcançar maior sucesso já foi dada. Está provado que o algoritmo de Grover é ideal. Não existe um algoritmo quântico capaz de resolver um problema com mais do que aceleração quadrática. A aceleração quadrática, embora não seja tão impressionante quanto exponencial, ainda oferece alguns benefícios. Ao trabalhar com grandes conjuntos de dados, qualquer aceleração pode ser valiosa.
É provável que o algoritmo de Grover encontre o aplicativo principal não para pesquisa, como foi apresentado acima, mas para suas variações. Em particular, a idéia de amplificar a amplitude pode ser útil.
Examinamos apenas alguns algoritmos, mas os algoritmos Shore e Grover são considerados os mais importantes. Existem muitos outros algoritmos baseados nas idéias inerentes a esses dois.1 Agora, voltemos nossa atenção dos algoritmos quânticos para outros campos de aplicação da computação quântica.