Práticas funcionais e frontend: mônadas e functores

Olá pessoal! Meu nome é Dmitry Rudnev, sou desenvolvedor front-end no BCS. Comecei minha jornada com o layout de interfaces de complexidade variada e sempre prestei atenção especial à interface: quão confortável seria para o usuário interagir com ele, se eu pudesse transmitir ao usuário a mesma interface que o designer pretendia.



Nesta série de artigos, quero compartilhar minha experiência de aplicação de práticas funcionais no desenvolvimento de front-end, falarei sobre os prós e contras que você receberá como desenvolvedor usando essas práticas. Se você gosta do tema, mergulharemos nos cantos mais secos e mais complexos do mundo funcional. Observo imediatamente que passaremos de maior para menor, ou seja, examinaremos o aplicativo clássico de uma vista de pássaro e, à medida que examinamos os artigos, desceremos para onde práticas específicas nos trarão benefícios visíveis.

Então, vamos começar manipulando os estados. Ao mesmo tempo, direi a você, mônadas e functores em geral.

Introdução

Ao desvendar a próxima interface e encontrar um terreno comum entre a interface do usuário e a análise, comecei a perceber que toda vez que um desenvolvedor lida com uma rede, ele só precisa processar todos os estados da interface do usuário e descrever a reação a um estado específico. E como cada um de nós busca a excelência, há um desejo de que essa maneira de processar os estados elabore um padrão que descreva da forma mais transparente possível o que está acontecendo e o que é o iniciador de uma reação específica e, como resultado, o resultado do trabalho. Felizmente, no mundo da programação, quase tudo o que você pode pensar foi implementado por alguém antes de você.

Tanto no mundo do desenvolvimento quanto no design, foram formados não apenas padrões que permitem resolver efetivamente seus problemas, mas também antipatters, que devem ser evitados por todos os meios, para que as más práticas não floresçam, e o desenvolvedor ou designer sempre teve presença em situações, quando não há solução concreta.

No nosso caso, a situação que a maioria dos desenvolvedores está processando todos os estados do elemento UI e reagindo a eles. O problema aqui é que o elemento da interface do usuário pode interagir com o estado local (sem fazer solicitações assíncronas) e com recursos ou repositórios remotos. Às vezes, os desenvolvedores esquecem de lidar com todos os casos extremos, o que leva a um comportamento inconsistente do sistema como um todo.

Todos os exemplos conterão exemplos de código usando a biblioteca React e um superconjunto de JavaScript - TypeScript, além de bibliotecas para programação funcional fp-ts.

Considere o exemplo mais simples, onde temos uma lista de elementos que solicitamos do servidor e precisamos exibir corretamente a interface do usuário de acordo com o resultado da solicitação. Estamos interessados ​​na função de render , porque nela precisamos exibir o estado correto durante a execução da solicitação. O código de exemplo completo pode ser visualizado em: aplicação simples . No futuro, estará disponível um projeto completo, focado em uma série de artigos, onde no curso desmontaremos suas partes individuais.

  const renderInitial = (...) => ...; const renderPending = (...) => ...; const renderError = (...) => ... ; const renderSuccess = (...) => ... ; return ( {state.subcribers.foldL( renderInitial, renderPending, renderError, renderSuccess, )} ); 

O exemplo mostra claramente que cada estado do modelo de dados tem sua própria função e cada função retorna um fragmento da interface do usuário prescrita para ele (mensagem, botão etc.). Olhando para o futuro, direi que o exemplo usa a RemoteData monad .

Isso é tão elegante e, o mais importante, seguro, podemos trabalhar com dados e respondê-los. Esta foi a introdução, na qual tentei demonstrar os benefícios de uma abordagem funcional em um exemplo aparentemente tão simples.

Functor e Mônada

Agora, vamos começar a mergulhar gradualmente na teoria aplicada das categorias e analisar conceitos como Functor e Monad , além de considerar práticas para trabalhar com dados com segurança usando práticas funcionais.

“Essencialmente, um functor nada mais é do que uma estrutura de dados que permite aplicar funções de transformação para extrair valores de um shell, modificá-los e colocá-los novamente no shell.

A inclusão de valores em um shell ou contêiner é um padrão de design fundamental na programação funcional, pois protege contra o acesso direto a valores, permitindo que eles sejam manipulados com segurança e sem alterações em programas aplicativos. ”

Tirei essa citação de um livro maravilhoso sobre a revisão de técnicas de programação funcional em JavaScript . Vamos começar com o componente teórico e analisar o que realmente é um functor. Para começar, precisamos nos familiarizar com uma seção fascinante da matemática chamada teoria das categorias no nível mais básico.

A teoria das categorias é um ramo da matemática que estuda as propriedades das relações entre objetos matemáticos, independentemente da estrutura interna dos objetos. A teoria das categorias ocupa um lugar central na matemática moderna; também encontrou aplicações em ciência da computação, lógica e física teórica.

Uma categoria consiste em objetos e setas que são direcionados entre eles. A maneira mais fácil de visualizar uma categoria é:

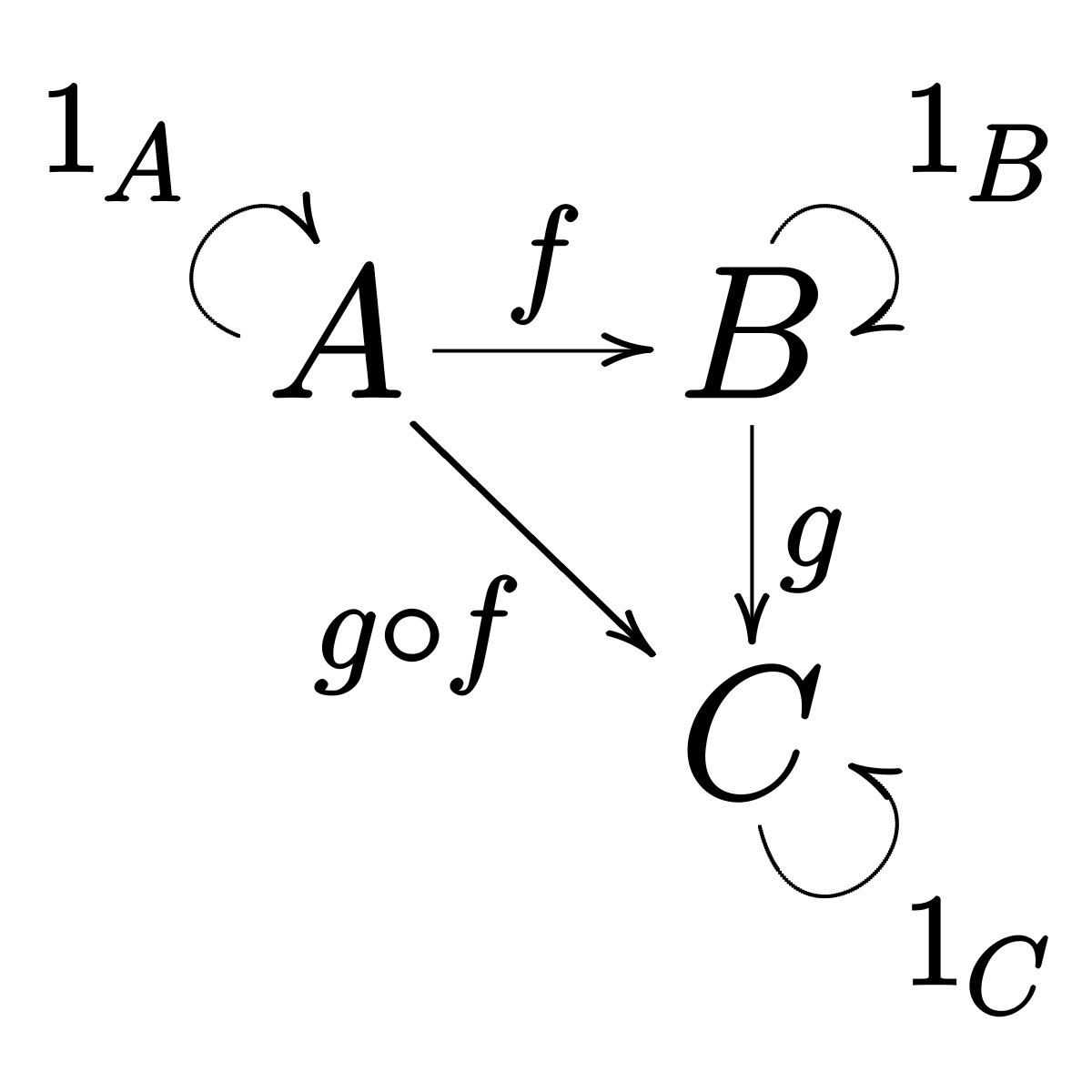
As setas são organizadas de modo que, se você possui uma seta do objeto A para o objeto B e uma seta do objeto B para C , deve haver uma seta - sua composição é de A a C. Pense nas setas como funções; eles também são chamados morfismos. Você tem uma função f que aceita A como argumento e retorna B. Há outra função g que aceita B como argumento e retorna C. Você pode combiná-las passando o resultado de f para g . Acabamos de descrever uma nova função que pega A e retorna C. Em matemática, essa composição é denotada por um pequeno círculo entre a notação de função: g ◦ f. Preste atenção à ordem da composição - da direita para a esquerda.

Em matemática, a composição é direcionada da direita para a esquerda. Nesse caso, ajuda se você ler g ◦ f como “g depois de f”.

 -—   A  B f :: A -> B -—   B   g :: B -> C -— A  C g . f 

Existem duas propriedades muito importantes que uma composição deve satisfazer em qualquer categoria.

1. A composição é associativa (associatividade é uma propriedade das operações que permite restaurar a sequência de sua execução na ausência de indicações explícitas de sucessão com igual prioridade; isso distingue entre associatividade esquerda, onde a expressão é avaliada da esquerda para a direita e associatividade direita da direita para a esquerda. Os operadores correspondentes são chamados associativos à esquerda e associativos à direita. Se você tiver três morfismos (setas), f, geh, que podem ser organizados (ou seja, seus tipos são consistentes entre si), você precisa de parênteses para agrupar-los. Matematicamente, isto é escrito como h ◦ (g ◦ f) = (h ◦ g) ◦ f = h ◦ g ◦ f (h ◦ g) ◦ f = h ◦ g ◦ f
2. Para cada objeto A existe uma seta, que será uma unidade de composição. Esta seta é de um objeto para si mesma. Ser uma unidade de composição significa que, ao compor uma unidade com qualquer seta que comece em A ou termine em A, respectivamente, a composição retornará a mesma seta. A seta da unidade de um objeto A é chamada IDa (unidade em A). Em notação matemática, se f passa de A para B, então f ◦ idA = f
   
   Para trabalhar com funções, uma única seta é implementada como uma função idêntica, que simplesmente retorna seu argumento.

Agora podemos considerar o que é um functor na teoria das categorias.

Um functor é um tipo especial de mapeamento entre categorias. Pode ser entendido como uma exibição que preserva a estrutura. Os functores entre pequenas categorias são morfismos na categoria de pequenas categorias. A totalidade de todas as categorias não é uma categoria no sentido usual, pois a totalidade de seus objetos não é uma classe. - Wikipedia .

Considere um exemplo de implementação de um functor para o contêiner Maybe, que é a idéia de um "valor que pode estar faltando".

 const compose = <A, B, C>( f: (a: A) => B, g: (b: B) => C, ): (a: A) => C => (a: A) => g(f(a)); //  Maybe: type Nothing = Readonly<{ tag: 'Nothing' }>; type Just<A> = Readonly<{ tag: 'Just'; value: A }>; export type Maybe<A> = Nothing | Just<A>; const nothing: Nothing = { tag: 'Nothing' }; const just = <A>(value: A): Just<A> => ({ tag: 'Just', value }); //    Maybe: const fmap = <A, B>(f: (a: A) => B) => (fa: Maybe<A>): Maybe<B> => { switch (fa.tag) { case 'Nothing': return nothing; case 'Just': return just(f(fa.value)); } }; //  1: fmap id === id namespace Laws { console.log( fmap(id)(just(42)), id(just(42)), ); // => { tag: 'Just', value: 42 } //  2: fmap f ◦ fmap g === fmap (f ◦ g) const f = (a: number): string => `Got ${a}!`; const g = (s: string): number => s.length; console.log( compose(fmap(f), fmap(g))(just(42)), fmap(compose(f, g))(just(42)), ); // => { tag: 'Just', value: 7 } } 

O método fmap pode ser visto de dois lados:

1. Como forma de aplicar uma função pura a um valor "em contêiner";
2. Como uma maneira de "elevar ao contexto do contêiner" uma função pura.

De fato, se os colchetes na interface forem ligeiramente diferentes, podemos obter a assinatura da função fmap :

 const fmap: <A, B>(f: (a: A) => B) => ((ma: Maybe<A>) => Maybe<B>); 

Tendo definido a interface:

 type Function1<Domain, Codomain> = (a: Domain) => Codomain; 

obtemos a definição de fmap :

 const fmap: <A, B>(f: (a: A) => B) => Function1<Maybe<A>, Maybe<B>>; 

Esse truque simples permite pensar em um functor como uma maneira de "elevar uma função pura para um contexto de contêiner". Graças a isso, é possível trabalhar com vários tipos de dados de maneira segura: por exemplo, processe com êxito cadeias de valores aninhados opcionais; Converter listas de dados lidar com exceções e muito mais.

Como explicado anteriormente, usando functors, você pode aplicar funções a valores de maneira segura e imutável. Mônadas são semelhantes aos functores, exceto pelo fato de poderem delegar lógica especial em casos especiais. O próprio functor sabe apenas como aplicar essa função e agrupar o resultado novamente em um shell, e ele não possui lógica adicional.

Uma mônada surge ao criar um tipo de dados inteiro pelo princípio de extrair dados pelo princípio de extrair valores de shells e definir regras de aninhamento. Assim como os functores, as mônadas são um modelo de design usado para descrever cálculos na forma de uma sequência de estágios em que o valor processado não é conhecido, mas são as mônadas que tornam possível controlar com segurança e sem efeitos colaterais o fluxo de dados quando eles são usados ​​na composição. Mônadas podem ter como objetivo resolver uma variedade de problemas. Teoricamente, as mônadas dependem do sistema de tipos em um idioma específico. De fato, muitas pessoas pensam que só podem ser entendidas se houver tipos de dados explícitos.

Para entender melhor as mônadas, os seguintes conceitos importantes devem ser aprendidos.

Mônada Fornece uma interface abstrata para operações monádicas
Tipo monádico. Implementação específica desta interface

Mas exemplos práticos da aplicação dessas propriedades de um functor e outras construções categóricas mostrarei em artigos futuros.