Sobre as coordenadas barentêntricas nos dedos

Oi

Certamente todo mundo testemunhou uma avaliação do grau de semelhança da criança com os pais: algo como "papai derramado, mas ele se parece com mamãe também !!!"


( tirada daqui )

Como no exemplo da imagem, você pode avaliar o grau de similaridade em porcentagem. Você também pode usar parentes para descrever com mais precisão a face do bebê na forma de uma soma ponderada de parentes de parentes ...

E parecerá e será percebido com naturalidade por uma pessoa "comum" que não esteja associada à antropologia, ou, por exemplo, à ciência forense. Para um profissional da área de análise e reconhecimento de faces, é mais provável que um rosto humano seja um conjunto de parâmetros. Ou seja, um ponto (um conjunto de coordenadas) em algum espaço com uma base (eixos correspondentes aos parâmetros). E se descrevermos a face da criança em comparação com seus parentes, provavelmente o ponto correspondente à face da criança aparecerá nesse espaço de parâmetros dentro do casco convexo da nuvem de pontos correspondentes às faces dos parentes mais próximos (mas isso não é exato).

Na verdade, sobre o que eu sou ... Essas duas abordagens para a descrição de faces correspondem a dois sistemas de coordenadas:

1. baricêntrica, descrição de um ponto no espaço (em nosso exemplo: face) por meio de uma mistura ponderada de outros pontos;
2. afim, uma descrição de um ponto no espaço através de coordenadas em alguma base.

Então, o que são coordenadas baricêntricas?

Deixe entrar -dimensional dado apontar com vetores de raio , . Além disso, nenhum dos pontos está na casca linear dos vetores de raio dos pontos restantes ... Simplificando, é bem simples: deixe esses pontos formarem uma figura que não pode ser totalmente representada em um espaço com dimensão menor que .

No caso do espaço unidimensional (linha), precisamos de 2 pontos não coincidentes, no caso do espaço bidimensional - um triângulo não degenerado, no caso da tridimensional - um tetraedro.

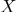
Então qualquer ponto no espaço pode ser representado por um vetor de raio :



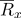
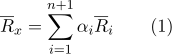
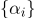
Definir e existem coordenadas baricêntricas.

Como as coordenadas bariêntricas são melhores / piores que afins?

Vamos começar com as desvantagens relativas:

1. na representação baricêntrica, precisamos de uma coordenada mais do que na afim;
2. a distância entre os pontos especificados barcentricamente não pode ser calculada diretamente nessas coordenadas.

Em parte, a primeira desvantagem é compensada pelo fato de que, apesar da necessidade de usar coordenadas bariêntricas ao descrever um ponto em Espaço -Dimensional, o número de graus não aumenta. As coordenadas baricêntricas definidas na fórmula (1) são relacionadas pela relação:



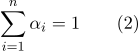
Quanto à segunda desvantagem, se houver necessidade de calcular a distância entre os pontos representados barcentricamente, faz sentido calcular produtos escalares e use o análogo da distância de Mahalanobis.

Quais são os bônus do uso de coordenadas baricêntricas?

1. As coordenadas baricêntricas são invariantes a transformações afins do espaço. Essa propriedade é usada, por exemplo, para interpolação linear em gráficos de computador. Permita que as coordenadas da textura sejam definidas nos vértices de um elemento de superfície triangular 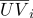e normais ( 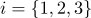), então cada ponto desta seção de superfície terá coordenadas bariêntricas 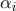suas coordenadas de textura 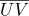e normal 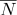pode ser calculado como:
   
   
   
   
   
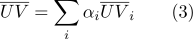
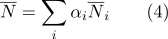
2. Por coordenadas barentêntricas, é fácil determinar se um ponto pertence 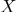partes do espaço delimitadas por um poliedro com vértices : isso é feito apenas se . A igualdade da i-ésima coordenada baricêntrica 1 significa que o ponto coincide com . Se várias coordenadas barocêntricas forem iguais a 0, isso significa que o ponto pertence a um subespaço estendido pelos vetores de raio dos pontos restantes cujas coordenadas correspondentes são maiores que 0.

Talvez eles sejam muito difíceis de calcular?

Não é mais complicado do que qualquer transformação linear do sistema de coordenadas. Porque, em essência, o cálculo das coordenadas baricêntricas é uma transformação.

Reescrevemos o vetor de raio dos pontos da seguinte forma:

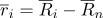
onde - um vetor radial no sistema de coordenadas centrado em um ponto .

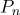
Em seguida, a fórmula (1) pode ser reescrita da seguinte forma:



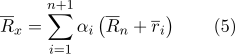
Vamos revelar os colchetes na soma:



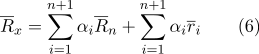
De acordo com a propriedade (2):



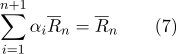
Por conseguinte:

,

onde

Dado (2), nos restringimos ao cálculo das primeiras coordenadas n baricêntricas. Imagine a transição para coordenadas barricêntricas como uma transformação linear:

,

onde - vetor n de coordenadas baricêntricas (exceto a última), - matriz de transformação.

Dadas as propriedades da representação barricêntrica, se for o caso substitua um dos vetores ( ), obtemos um vetor com zero componentes, exceto um i-ésimo, que será igual a 1.

Se a matriz multiplicar por matriz composta de colunas de , devemos obter a matriz de identidade (uma matriz com as na diagonal principal e zeros nos elementos restantes):

,

onde , A matriz de identidade ( - símbolo Kronecker: 1 se caso contrário, 0).

De (10) encontramos :



Assim, ter um conjunto de pontos com vetores de raio , podemos calcular a matriz para converter em coordenadas baricêntricas:



Usando essa matriz, podemos obter o primeiro coordenadas de ponto barcentric com vetor de raio :



Utilizando a relação (2) novamente, obtemos a última coordenada baricêntrica:

Conclusão

Talvez à primeira vista, o baricêntrico também pareça estranho e complexo. Mas, de fato, essa é uma ferramenta muito conveniente e indispensável em muitas tarefas, às quais você se acostuma rapidamente. Porque não há mágica aqui, é álgebra linear em sua forma mais pura!