 Você pode baixar o arquivo com o código e os dados na postagem original no meu blog
Você pode baixar o arquivo com o código e os dados na postagem original no meu blogExiste um projeto muito interessante - "
Código Rosetta" . Seu objetivo é “apresentar a solução dos mesmos problemas no maior número possível de diferentes linguagens de programação, a fim de demonstrar seus lugares e diferenças comuns e ajudar uma pessoa que tem o conhecimento a resolver o problema com um método para aprender outro”.
Este recurso oferece uma oportunidade única de comparar códigos de programa em diferentes idiomas, o que faremos neste artigo. É uma revisão e aprimoramento completos do artigo de John MacLoon "
Comprimento do código medido em 14 idiomas ".
Importar e analisar dados
Vamos começar criando uma modificação na função
Importar que armazenará dados para uso futuro, para não solicitá-los posteriormente ao servidor.
Clear[importOnce]; importOnce[args___]:=importOnce[args]=Import[args]; If[FileExistsQ[#], Get[#], Null]&@FileNameJoin[{NotebookDirectory[], "importOnce.mx"}]
Crie um analisador para importar dados.
Clear[createPageLinkDataset]; createPageLinkDataset[baseLink_]:=createPageLinkDataset[baseLink]=Cases[Cases[Import[baseLink, "XMLObject"], XMLElement["div", {"class"->"mw-content-ltr", "dir"->"ltr", "lang"->"en"}, data_]:>data, Infinity], XMLElement["li", {}, {XMLElement["a", {___, "href"->link_, ___}, {name_}]}]:><|"name"->name, "link"->"http://rosettacode.org"<>link|>, Infinity]; If[FileExistsQ[#], Get[#], Null]&@FileNameJoin[{NotebookDirectory[], "createPageLinkDataset.mx"}]
Importamos a lista de todas as linguagens de programação suportadas pelo projeto (já existem mais de 750):
$Languages=createPageLinkDataset["http://rosettacode.org/wiki/Category:Programming_Languages"]; Dataset@$Languages

Criaremos funções para traduzir o nome em um link e vice-versa; isso será útil mais tarde:
langLinkToName[link_String]:=langLinkToName[link]=SelectFirst[$Languages, #[["link"]]==link&]["name"]; langNameToLink[name_String]:=langNameToLink[name]=SelectFirst[$Languages, #[["name"]]==name&]["link"];
Carregaremos a lista de tarefas resolvidas em cada uma das linguagens de programação. A análise foi projetada para que nem todos os links para páginas sejam tarefas. Vamos limpá-los mais tarde.
$LangTasksAllPre=Map[<|"name"->#["name"], "link"->#["link"], "tasks"->createPageLinkDataset[#["link"]][[All, "link"]]|>&, $Languages]; Dataset@$LangTasksAllPre

Calculamos uma lista de todas as tarefas em potencial que podem ser resolvidas no projeto (são pouco mais de 2600):
$TasksPre=DeleteDuplicates[Flatten[$LangTasksAllPre[[;;, "tasks"]]]]; Length[$TasksPre]

Vamos criar uma função que captura todos os fragmentos de código na página de tarefas.
ClearAll[codeExtractor]; codeExtractor[link_String]:=Module[{code, positions, rawData}, code=importOnce[link, "XMLObject"]; positions=Map[{#[[1, 1;;-2]], Partition[#[[;;, -1]], 2, 1]}&, DeleteCases[ Gather[ Position[code, XMLElement["h2", _, title_]], And[Length[#1]==Length[#2], #1[[1;;-2]]==#2[[1;;-2]]]&], x_/; Length[x]==1]]; rawData=Framed/@Flatten[Map[ With[{pos=#[[1]]}, Map[Extract[code, pos][[#[[1]];;#[[2]]-1]]&, #[[2]]]]&, positions], 1]; Association@DeleteCases[Map[langLinkToName[("link"/.#)]->("code"/.#)&, Map[ KeyValueMap[If[#1==="link", #1->#2[[1]], #1->#2]&, Merge[SequenceSplit[Cases[#, Highlighted[x_, ___]:>x, Infinity], {"Output"}][[1]], Identity]]&, rawData/.{XMLElement["h2", _, title_]:>Cases[title, XMLElement["a", {___, "href"->linkInner_/; MemberQ[$Languages[[;;, "link"]], "http://rosettacode.org"<>linkInner], ___}, {___}]:>Highlighted[<|"link"->"http://rosettacode.org"<>linkInner|>], Infinity], XMLElement["div", {}, x_/; Not[FreeQ[x, "Output:"]]]:>Highlighted["Output"], XMLElement["pre", _, code_]:>Highlighted[<|"code"->Check[StringJoin@Flatten[code//.XMLElement["span", _, codeFragment_]:>codeFragment//.XMLElement["br", {"clear"->"none"}, {}]:>"\n"//.XMLElement["a", {___}, codeFragment_]:>codeFragment//.XMLElement["b", {}, {x_}]:>x//.XMLElement["big", {}, {x_}]:>x//.XMLElement["sup", {}, x_]:>Flatten[x]//.XMLElement["sub", {}, x_]:>Flatten[x]//.XMLElement[_, {___}, x_]:>Flatten[x]], Echo[StringJoin@Flatten[code//.XMLElement["span", _, codeFragment_]:>codeFragment//.XMLElement["br", {"clear"->"none"}, {}]:>"\n"//.XMLElement["a", {___}, codeFragment_]:>codeFragment//.XMLElement["b", {}, {x_}]:>x//.XMLElement["big", {}, {x_}]:>x//.XMLElement["sup", {}, x_]:>Flatten[x]//.XMLElement["sub", {}, x_]:>Flatten[x]//.XMLElement[_, {___}, x_]:>Flatten[x]]]]|>, Background->Red]} ]], _->"code"]];
Agora vamos processar todas as páginas:
ClearAll[taskCodes]; taskCodes[link_]:=taskCodes[link]=Check[codeExtractor[link], Echo[link]]; If[FileExistsQ[#], Get[#], taskCodes/@$TasksPre; DumpSave[#, taskCodes]]&@FileNameJoin[{NotebookDirectory[], "taskCodes.mx"}];
Um exemplo do que a função produz:
Dataset[taskCodes[$TasksPre[[20]]]]
Selecione as páginas de tarefas (aquelas com pelo menos um pedaço de código):
$taskLangs=DeleteCases[{#, taskCodes[#]}&/@$TasksPre, {_, <||>}];
$langTasks=Map[<|"name"->#[["name"]], "link"->#[["link"]], "tasks"->With[{lang=#[["name"]]}, Select[$taskLangs, MemberQ[Keys[#[[2]]], lang]&][[;;, 1]]]|>&, $Languages]; Dataset[$langTasks]

Uma lista de tarefas e funções que convertem o nome da tarefa em um link e vice-versa:
$Tasks=<|"name"->StringReplace[URLDecode[StringReplace[#, "http://rosettacode.org/wiki/"->""]], {"_"->" ", "/"->" -> "}], "link"->#|>&/@$taskLangs[[;;, 1]]; taskLinkToName[link_String]:=langLinkToName[link]=SelectFirst[$Tasks, #[["link"]]==link&]["name"]; taskNameToLink[name_String]:=langNameToLink[name]=SelectFirst[$Tasks, #[["name"]]==name&]["link"];
Estatísticas simples
Para vários idiomas, ainda não há um problema resolvido:
WordCloud[1/StringLength[#]->#&/@Select[$langTasks, Length[#["tasks"]]==0&][[All, "name"]], ImageSize->{1200, 800}, MaxItems->All, WordOrientation->{

Lista de idiomas que resolveram problemas:
$LanguagesWithTasks=Select[$langTasks, Length[#["tasks"]]=!=0&][[All, "name"]]; Length[$LanguagesWithTasks]
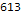
Distribuição do número de problemas resolvidos por idioma:
Histogram[Length/@$langTasks[[;;, "tasks"]], 50, PlotRange->All, BarOrigin->Bottom, AspectRatio->1/2, ImageSize->700, Background->White, Frame->True, GridLines->Automatic, FrameLabel->Map[Style[#, 20]&, {" ", lg[" "]}], ScalingFunctions->"Log10", PlotLabel->Style[" ", 20]]
Distribuição do número de idiomas por tarefas resolvidas:
Histogram[Length/@$taskLangs[[;;, 2]], 50, PlotRange->All, AspectRatio->1/2, ImageSize->700, Background->White, Frame->True, GridLines->Automatic, FrameLabel->Map[Style[#, 20]&, {" ", " "}], PlotLabel->Style[" ", 20]]

Idiomas em que os problemas mais resolvidos são:
BarChart[#1[[;;, 2]], PlotRangePadding->0, BarSpacing -> 0.1, BarOrigin -> Left, AspectRatio -> 1, ImageSize -> 1000, ChartLabels -> #1[[;;, 1]], Frame -> True, GridLines -> {Range[0, 10^3, 50], None}, ColorFunction -> ColorData["Rainbow"], FrameLabel->{{None, None}, Style[#, FontFamily->"Open Sans Light", 16]&/@{" ", " "}}, FrameTicks->{Automatic, {All, All}}, Background->White] &@DeleteCases[SortBy[{#[["name"]], Length[#[["tasks"]]]}&/@$langTasks, Last], {_, x_/; x<200}]

Tarefas resolvidas no maior número de linguagens de programação:
BarChart[#1[[;;, 2]], PlotRangePadding->0, BarSpacing -> 0.2, BarOrigin -> Left, AspectRatio -> 1.6, ImageSize -> 1000, ChartLabels -> #1[[;;, 1]], Frame -> True, GridLines -> {Range[0, 10^3, 50], None}, ColorFunction -> ColorData["Rainbow"], FrameLabel->{{None, None}, Style[#, FontFamily->"Open Sans Light", 16]&/@{" ", " "}}, FrameTicks->{Automatic, {All, All}}, Background->White] &@DeleteCases[SortBy[{taskLinkToName[#[[1]]], Length[#[[2]]]}&/@$taskLangs, Last], {_, x_/; x<100}]

Tarefas que possuem uma solução para um determinado conjunto de linguagens de programação
Uma função que exibe tarefas resolvidas em uma ou mais linguagens de programação ao mesmo tempo:
commonTasks[lang_String]:=commonTasks[lang]=Sort[SelectFirst[$langTasks, #["name"]==lang&][["tasks"]]]; commonTasks["Mathematica"]:=commonTasks["Mathematica"]=Union[commonTasks["Wolfram Language"], Sort[SelectFirst[$langTasks, #["name"]=="Mathematica"&][["tasks"]]]]; commonTasks[lang_List]:=commonTasks[lang]=Sort[Intersection@@(commonTasks/@lang)];
Tarefas comuns aos 25 primeiros idiomas mais populares (o tamanho da fonte corresponde ao número relativo de idiomas nos quais o problema foi resolvido):
WordCloud[With[{tasks=taskLinkToName/@commonTasks[SortBy[{#[["name"]], Length[#[["tasks"]]]}&/@$langTasks, Last][[-25;;-1]][[;;, 1]]]}, Transpose@{tasks, tasks/.Rule@@@SortBy[{taskLinkToName[#[[1]]], Length[#[[2]]]}&/@$taskLangs, Last]}], ImageSize->{1000, 1000}, MaxItems->All, WordOrientation->{

Função para medir o comprimento do código
Em seguida, precisamos de uma métrica para estimar o comprimento do código. Geralmente, acredita-se que este é o número de linhas de código:
SetAttributes[lineCount, Listable] lineCount[str_String]:=StringCount[StringReplace[StringReplace[str, {" "->"", "\t"->""}], "\n"..->"\n"], "\n"]+1;
Mas como esse parâmetro é significativamente afetado pela marcação do código (no final, digamos, no Wolfram Langiuage (
Mathematica ), você pode escrever vários comandos em uma linha ao mesmo tempo), usaremos o número de caracteres que não são espaços como métrica.
SetAttributes[characterCount, Listable] characterCount[str_String]:=StringLength[StringReplace[str, WhitespaceCharacter->""]];
Essa métrica não fica nas mãos do
Mathematica com seus longos nomes descritivos de comando (que é sem dúvida uma grande vantagem fora deste blog); portanto, também implementamos uma métrica baseada na contagem de tokens (objetos "simbólicos"), para os quais usaremos palavras individuais separadas por qualquer caractere que não seja a carta.
SetAttributes[tokens, Listable] tokens[str_String]:=DeleteCases[StringSplit[str, Complement[Characters@FromCharacterCode[Range[1, 127]], CharacterRange["a", "z"], CharacterRange["A", "Z"], CharacterRange["0", "9"], {"."}]], ""]; tokenCount[str_String]:=Length[tokens[str]];
Medição do comprimento do código
Temos um conjunto de dados sobre cada tarefa:
$taskData=Map[<|"name"->#[[1]], "lineCount"->Map[lineCount, #[[2]]], "characterCount"->Map[characterCount, #[[2]]], "tokens"->Map[Flatten[tokens[#]]&, #[[2]]]|>&, $taskLangs]; Dataset[$taskData]

Uma função que coleta estatísticas para cada idioma em relação a todas as tarefas resolvidas:
Clear[langData]; langData[name_]:=langData[name]=<|"name"->name, "lineCount"->If[name==="Mathematica", DeleteMissing[AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "lineCount"]], name]]]~Join~DeleteMissing[AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "lineCount"]], "Wolfram Language"]]], AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "lineCount"]], name]]], "characterCount"->If[name==="Mathematica", DeleteMissing[AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "characterCount"]], name]]]~Join~DeleteMissing[AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "characterCount"]], "Wolfram Language"]]], AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "characterCount"]], name]]], "tokens"->If[name==="Mathematica", DeleteMissing[AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "tokens"]], name]]]~Join~DeleteMissing[AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "tokens"]], "Wolfram Language"]]], AssociationThread[#[[;;, "name"]]->Lookup[#[[;;, "tokens"]], name]]]|>&@(With[{task=#}, SelectFirst[$taskData, #[["name"]]==task&]]&/@commonTasks[name]); Map[langData, $LanguagesWithTasks];
Uma função que compara métricas de comparação para duas (ou mais) linguagens de programação com base em todas as tarefas comuns:
ClearAll[compareLanguagesData, compareLanguages]; compareLanguagesData[langs_List/; Length[langs]>=2]:=compareLanguagesData[langs]=Module[{tasks, data}, tasks=commonTasks[langs]; data=langData/@langs; <|"lineCount"->Transpose[Lookup[#[["lineCount"]], tasks][[;;, 1]]&/@data], "characterCount"->Transpose[Lookup[#[["characterCount"]], tasks][[;;, 1]]&/@data], "tokensCount"->Transpose[Lookup[Map[Length, #[["tokens"]]], tasks]&/@data]|> ]; compareLanguages[langs_List/; Length[langs]>=2, function_]:=Module[{data}, data=compareLanguagesData[langs]; Map[Map[function, #]&, data] ];
Análise e visualização
Agora podemos obter muitas análises.
Para começar, comparamos os indicadores absolutos. A função abaixo cria um gráfico no qual os pontos mostram os valores correspondentes para dois idiomas. Se o ponto estiver abaixo da linha diagonal (a escala ao longo dos eixos é diferente, geralmente se o comprimento do código variar bastante), isso significa que o idioma da parte inferior "venceu", caso contrário, o idioma é "de cima".
compareGraphic[{lang1_, lang2_}]:= Grid[{#[[1;;2]], {#[[3]], SpanFromLeft}}&@KeyValueMap[Graphics[{Map[{If[#[[1]]<#[[2]], Orange, Darker@Green], Point[#]}&, #2], AbsoluteThickness[2], Gray, InfiniteLine[{{0, 0}, {1, 1}}]}, PlotRangePadding->0, GridLines->Automatic, AspectRatio->1, PlotRange->All, Frame->True, ImageSize->500, Background->White, FrameLabel->(Style[#/."Mathematica"->"Wolfram Language (Mathematica)", 16, FontFamily->"Open Sans Light"]&/@{lang1, lang2}), PlotLabel->(Style[(#1/.{"lineCount"->" ", "characterCount"->" ", "tokensCount"->" "}), 20, FontFamily->"Open Sans Light"])]&, compareLanguages[{lang1, lang2}, Identity]], Background->White]
Você pode ver claramente que o código da Wolfram Language é sempre quase menor que o código C:
compareGraphic[{"Mathematica", "C"}]

Ou Pytnon:
compareGraphic[{"Mathematica", "Python"}]

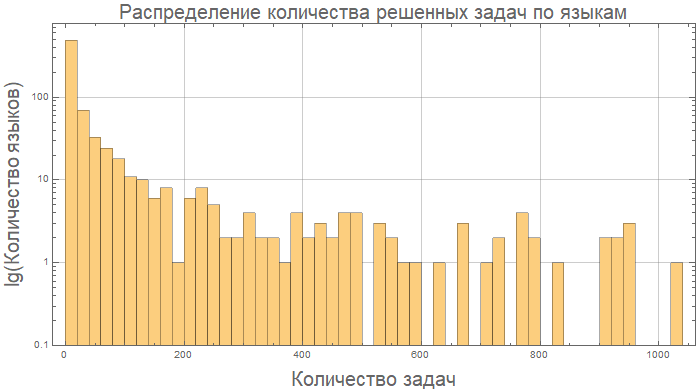
E aqui, por exemplo, Kotlin e Java são essencialmente "iguais" em termos de tamanho do código:
compareGraphic[{"Kotlin", "Java"}]
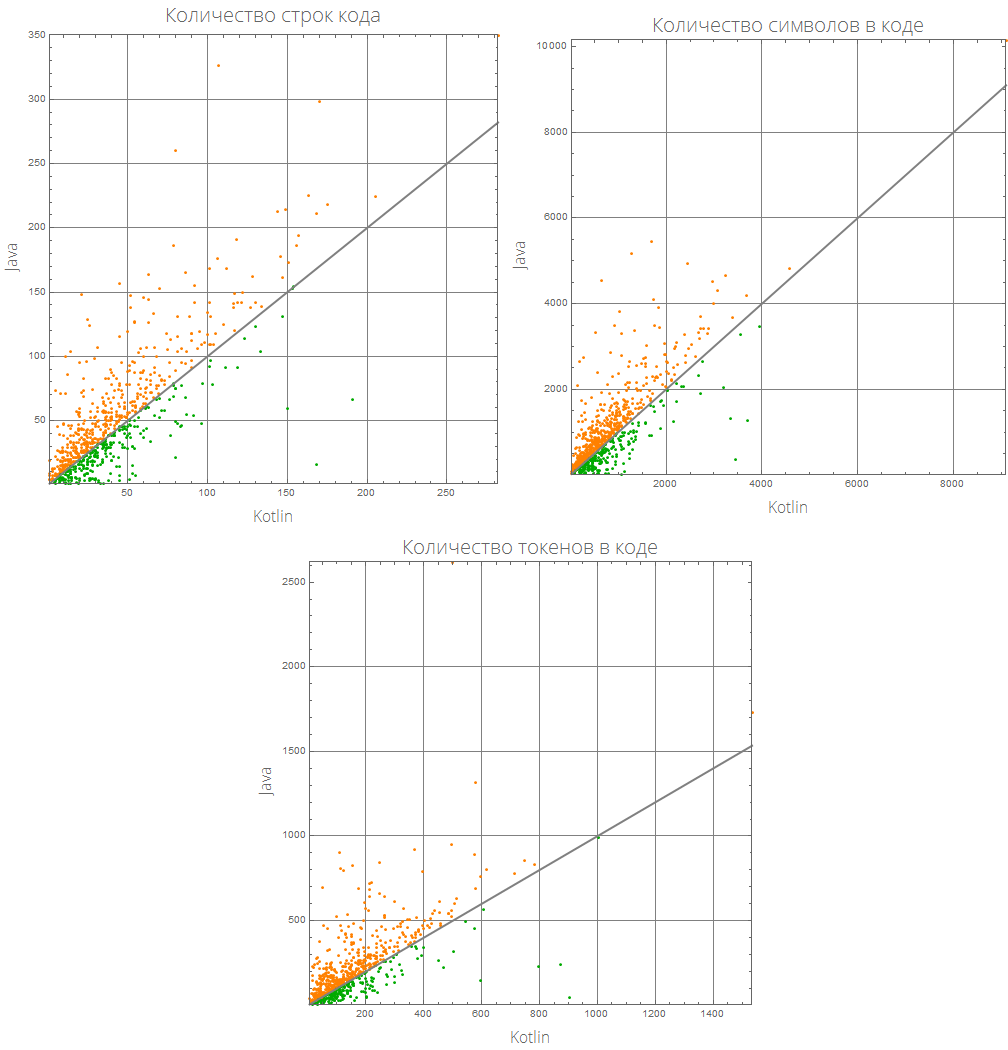
Essa representação gráfica pode ser mais informativa:
comparePlot[{lang1_, lang2_}]:= Grid[{#[[1;;2]], {#[[3]], SpanFromLeft}}&@KeyValueMap[ListLinePlot[Sort@#2, GridLines->Automatic, AspectRatio->1, PlotRange->{Automatic, {0, 2}}, Frame->True, ImageSize->500, Background->White, FrameLabel->(Style[#/."Mathematica"->"Wolfram Language (Mathematica)", 16, FontFamily->"Open Sans Light"]&/@{lang1, lang2}), PlotLabel->(Style[(#1/.{"lineCount"->" ", "characterCount"->" ", "tokensCount"->" "}), 20, FontFamily->"Open Sans Light"]), ColorFunction->(If[#2>1, Orange, Darker@Green]&), ColorFunctionScaling->False, PlotStyle->AbsoluteThickness[3]]&, compareLanguages[{lang1, lang2}, Divide[#[[1]], #[[2]]]&]], Background->White]
comparePlot[{"Mathematica", "R"}]
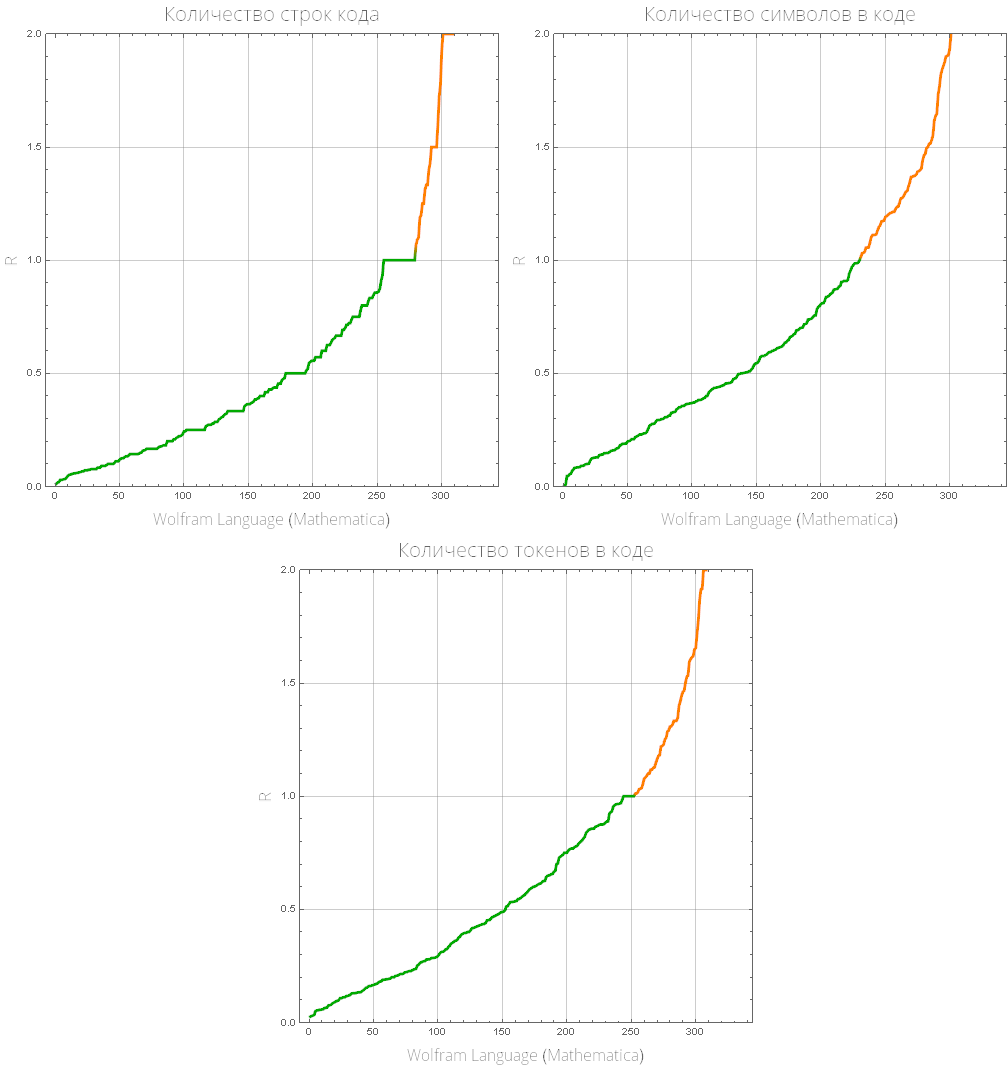
comparePlot[{"BASIC", "ALGOL 68"}]
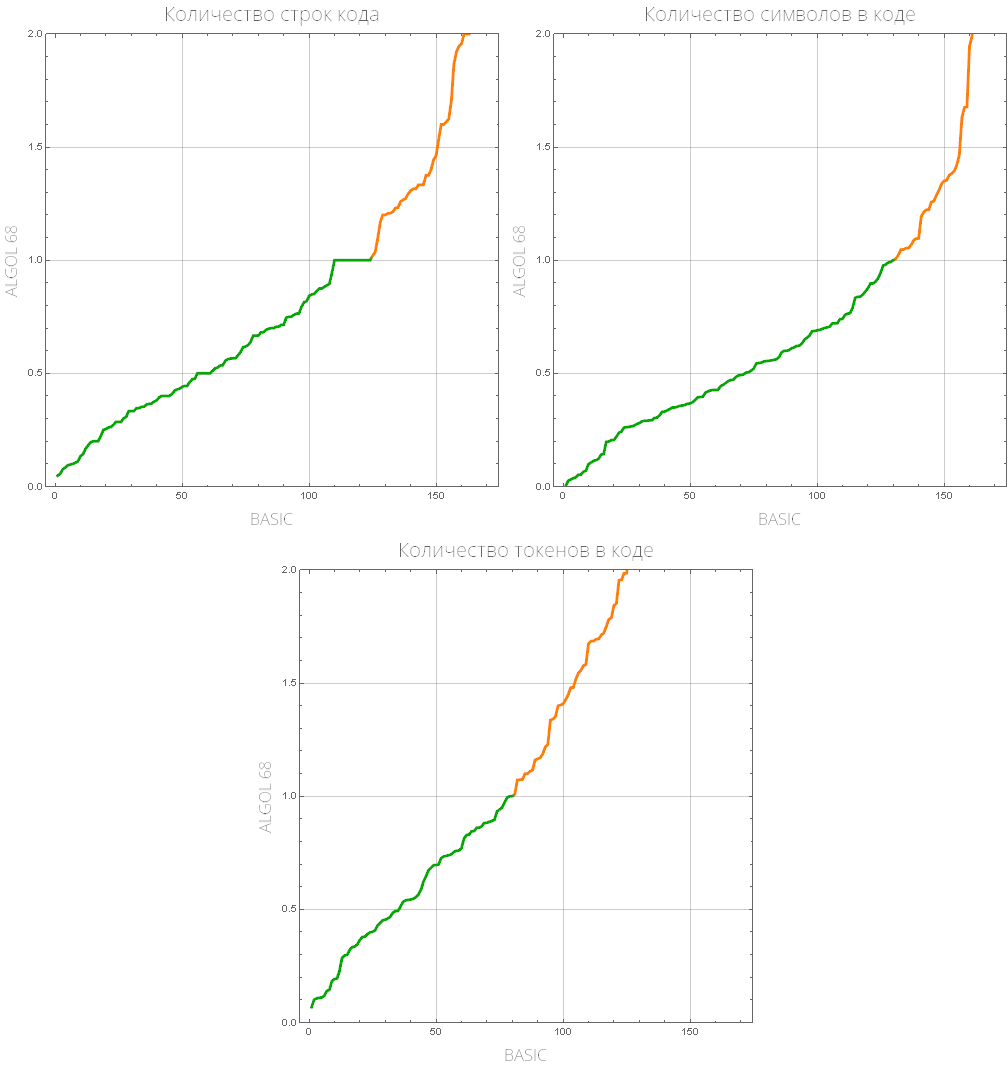
Definimos uma função que exibirá uma lista de linguagens de programação "populares" (aquelas com o maior número de tarefas resolvidas):
Clear[$popularLanguages]; $popularLanguages[n_/; n>2]:=$popularLanguages[n]=Reverse[SortBy[{#[["name"]], Length[#[["tasks"]]]}&/@$langTasks, Last][[-n;;-1]]]
$popularLanguages[25]

Visualizamos a lista dos primeiros 350 idiomas (é assim que o protetor de tela para este post foi criado no início):
WordCloud[$popularLanguages[350], ColorNegate@Binarize@ImageCrop@Import@"D:\\YandexDisk\\WolframMathematicaRuFiles\\388-3885229_rosetta-stone-silhouette-stone-silhouette-png-transparent-png.png", ImageSize->1000, MaxItems->All, WordOrientation->{

Uma função que exibe a análise do comprimento do código em diferentes métricas para os n primeiros idiomas populares:
ClearAll[langMetricsGrid]; langMetricsGrid[n_Integer, type_, OptionsPattern[{"SortQ"->True, "measureFunction"->Mean}]]:=Module[{$nPL, $pl, tableData, scale, notSortedTableData, order, fullTableData, min, max, orderedMeans, meanFunction}, $nPL=n; meanFunction[{lang1_, lang2_}]:=Quiet[Map[Median[N[#]]&, compareLanguages[{lang1, lang2}, Divide[#[[1]], #[[2]]]&]/.ComplexInfinity->Nothing/.Indeterminate->Nothing]]; $pl=$popularLanguages[$nPL][[;;, 1]]; tableData=Quiet@Table[If[i==j, "", meanFunction[{$pl[[i]], $pl[[j]]}][[type]]], {i, 1, $nPL}, {j, 1, $nPL}]; order=If[OptionValue["SortQ"], Ordering[tableData, All, OptionValue["measureFunction"][#1/.""->Nothing]<OptionValue["measureFunction"][#2/.""->Nothing]&], Range[1, $nPL]]; orderedMeans=Round[If[OptionValue["SortQ"], Map[Mean, tableData/.""->Nothing][[order]], Map[Mean, tableData/.""->Nothing]], 1/1000]//N; {min, max}=MinMax[Cases[Flatten[tableData], _?NumericQ]]; scale=Function[Evaluate[Rescale[#, {min, max}, {0, 1}]]]; fullTableData=Transpose[{{""}~Join~$pl[[order]]}~Join~{{""}~Join~orderedMeans}~Join~Transpose[{Map[Rotate[#, 90Degree]&, $pl]}~Join~ReplaceAll[tableData, x_?NumericQ:>Item[Round[x, 1/100]//N, Background->Which[x<1, LightGreen, x==1, LightBlue, x>1, LightRed]]][[order]]/.""->Item["", Background->Gray]]]; Framed[Labeled[Style[Row[{" ", Style[type/.{"lineCount"->" ", "characterCount"->" ", "tokensCount"->" "}, Bold], "\n "}], 22, FontFamily->"Open Sans Light", TextAlignment->Center], Grid[fullTableData, Background->White, ItemStyle->Directive[FontSize -> 12, FontFamily->"Open Sans Light"], Dividers->White]], FrameStyle->None, Background->White]];
O valor mediano da proporção do número de linhas de código na resolução de problemas em diferentes linguagens de programação:
langMetricsGrid[25, "lineCount", "SortQ"->False]

Se você classificar a tabela pela coluna "Média", será mais óbvio - a Wolfram Language (Mathematica) leva:
langMetricsGrid[25, "lineCount", "SortQ"->True]
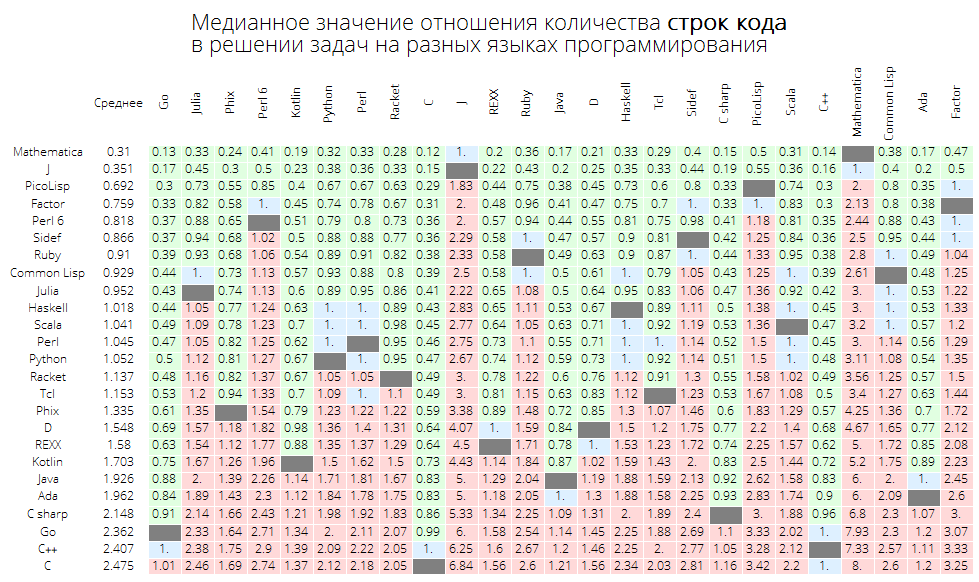
O valor mediano da proporção do número de caracteres no código na resolução de problemas em diferentes linguagens de programação:
langMetricsGrid[25, "characterCount", "SortQ"->True]

O valor mediano da proporção do número de tokens no código na resolução de problemas em diferentes linguagens de programação:
langMetricsGrid[25, "tokensCount", "SortQ"->True]

As mesmas tabelas podem ser construídas, digamos, para os 50 primeiros idiomas mais populares:
langMetricsGrid[50, "lineCount", "SortQ"->True] langMetricsGrid[50, "characterCount", "SortQ"->True] langMetricsGrid[50, "tokensCount", "SortQ"->True]



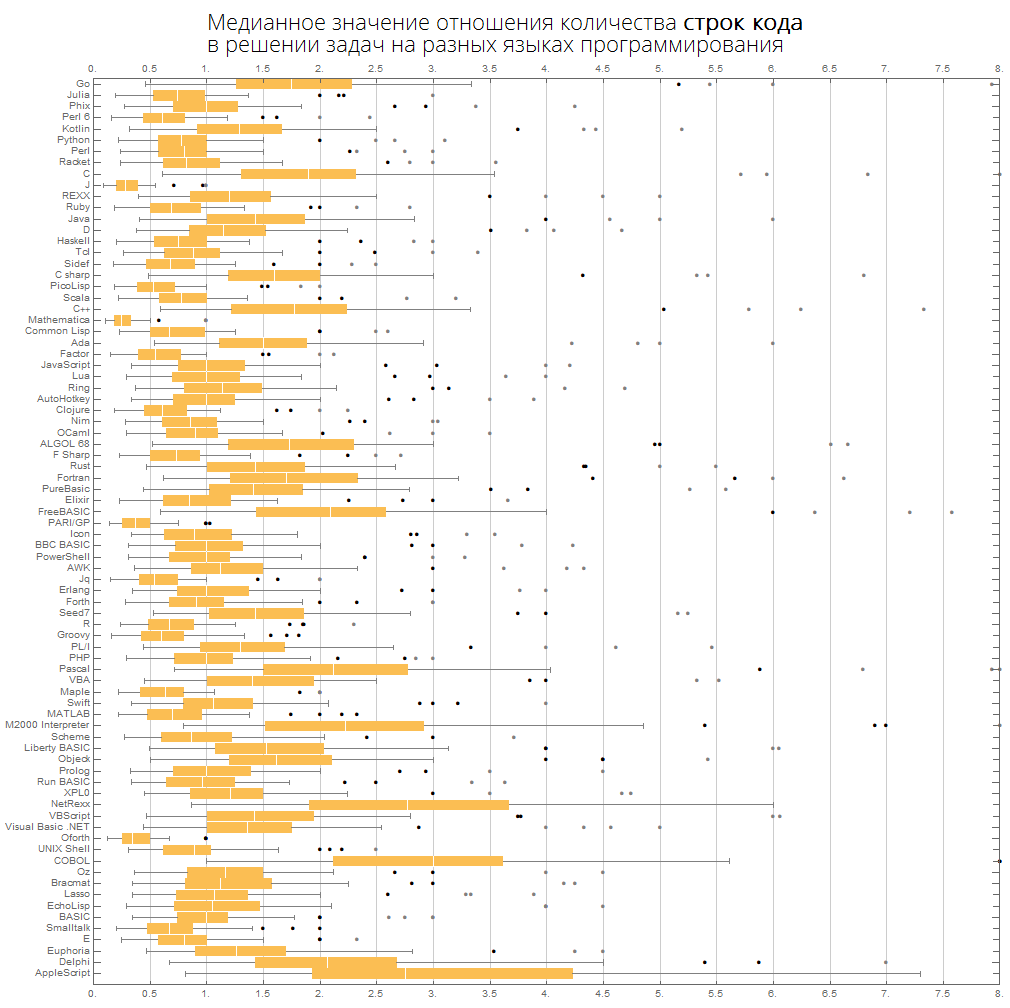
Podemos imaginar as mesmas informações de forma mais compacta - na forma de caixas com bigode (diagrama de caixas e bigodes):
ClearAll[langMetricsBoxWhiskerChart]; langMetricsBoxWhiskerChart[n_Integer, type_, OptionsPattern[{"SortQ"->True, "measureFunction"->Mean}]]:=Module[{$nPL, $pl, tableData, scale, notSortedTableData, order, fullTableData, min, max, orderedMeans, meanFunction}, $nPL=n; meanFunction[{lang1_, lang2_}]:=Quiet[Map[Median[N[#]]&, compareLanguages[{lang1, lang2}, Divide[#[[1]], #[[2]]]&]/.ComplexInfinity->Nothing/.Indeterminate->Nothing]]; $pl=Reverse@$popularLanguages[$nPL][[;;, 1]]; tableData=Quiet@Table[If[i==j, "", meanFunction[{$pl[[i]], $pl[[j]]}][[type]]], {i, 1, $nPL}, {j, 1, $nPL}]; order=If[OptionValue["SortQ"], Ordering[tableData, All, OptionValue["measureFunction"][#1/.""->Nothing]>OptionValue["measureFunction"][#2/.""->Nothing]&], Range[1, $nPL]]; Framed[Labeled[Style[Row[{" ", Style[type/.{"lineCount"->" ", "characterCount"->" ", "tokensCount"->" "}, Bold], "\n "}], 22, FontFamily->"Open Sans Light", TextAlignment->Center], BoxWhiskerChart[tableData[[order]], "Outliers", ChartLabels->$pl[[order]], BarOrigin->Left, ImageSize->1000, AspectRatio->1, GridLines->{Range[0, 20, 1/2], None}, FrameTicks->{Range[0, 20, 0.5], Automatic}, PlotRangePadding->0, PlotRange->{{0, 8}, Automatic}, Background->White] ], FrameStyle->None, Background->White]];
Os idiomas são classificados por popularidade (o diagrama mostra a proporção do número de linhas de código entre os idiomas):
langMetricsBoxWhiskerChart[80, "lineCount", "SortQ"->False]
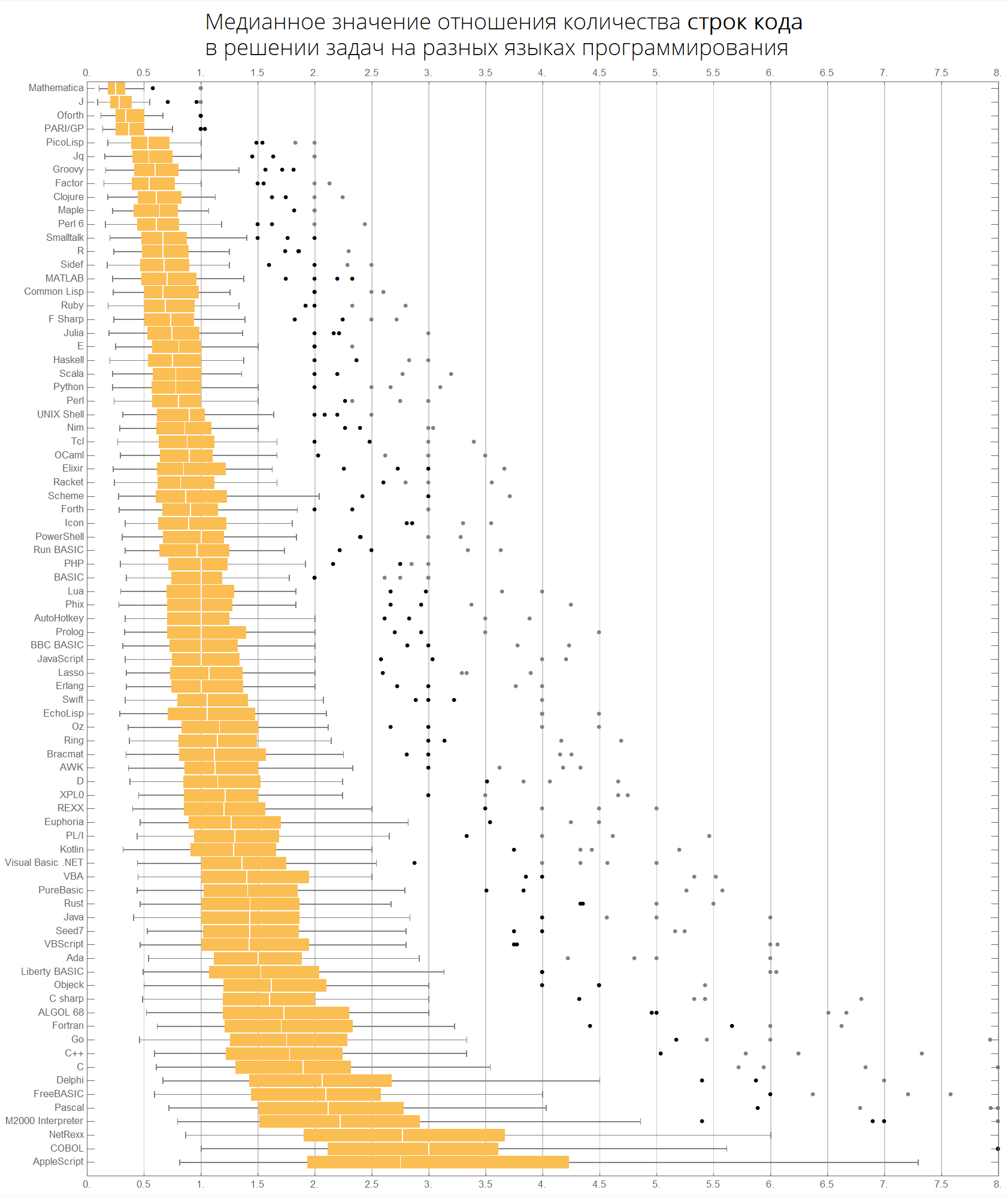
Por valor mediano:
langMetricsBoxWhiskerChart[80, "lineCount", "SortQ"->True]
Por fim, gráficos relacionados ao número de caracteres e tokens:
langMetricsBoxWhiskerChart[80, "characterCount", "SortQ"->True] langMetricsBoxWhiskerChart[80, "tokensCount", "SortQ"->True]
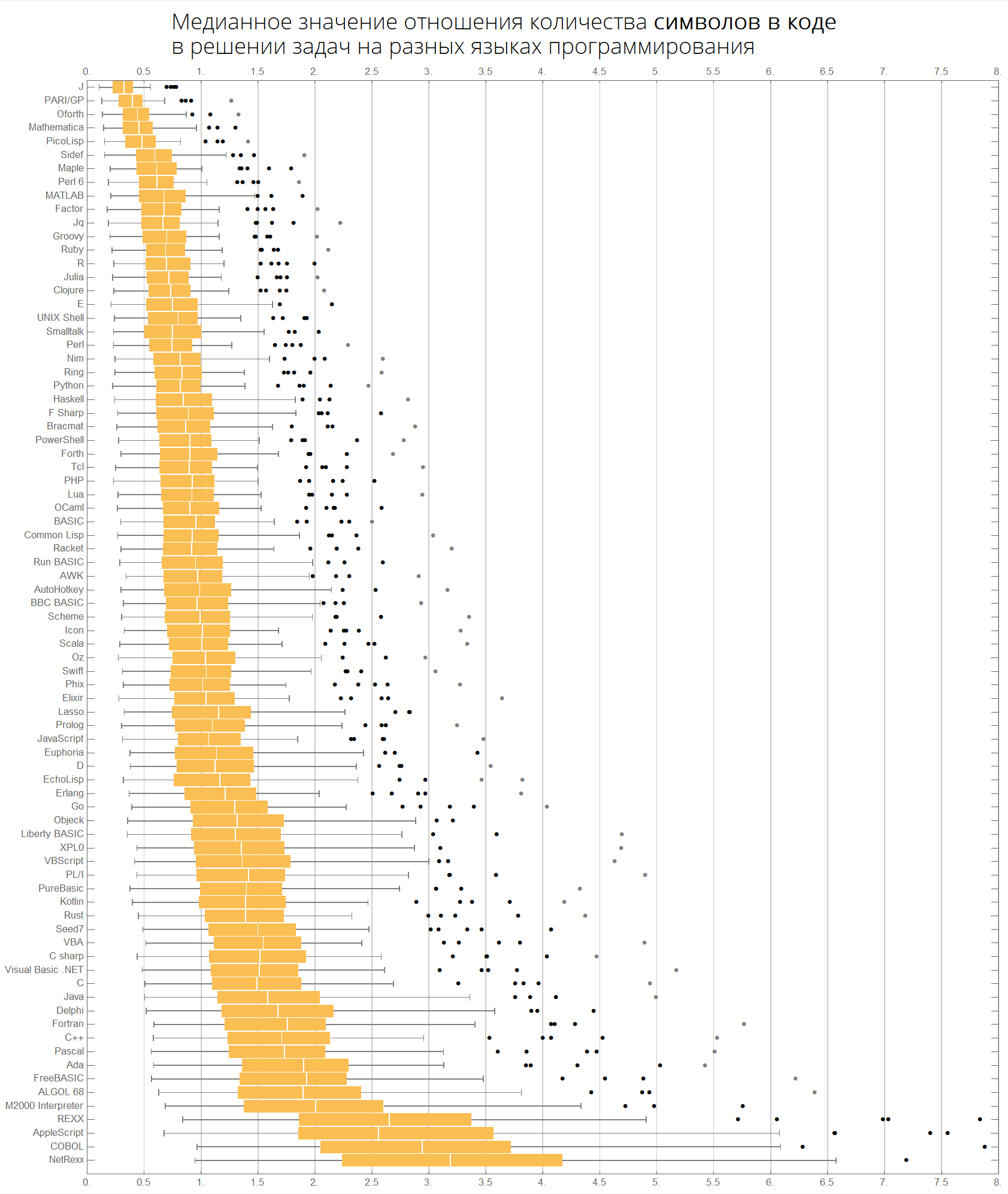
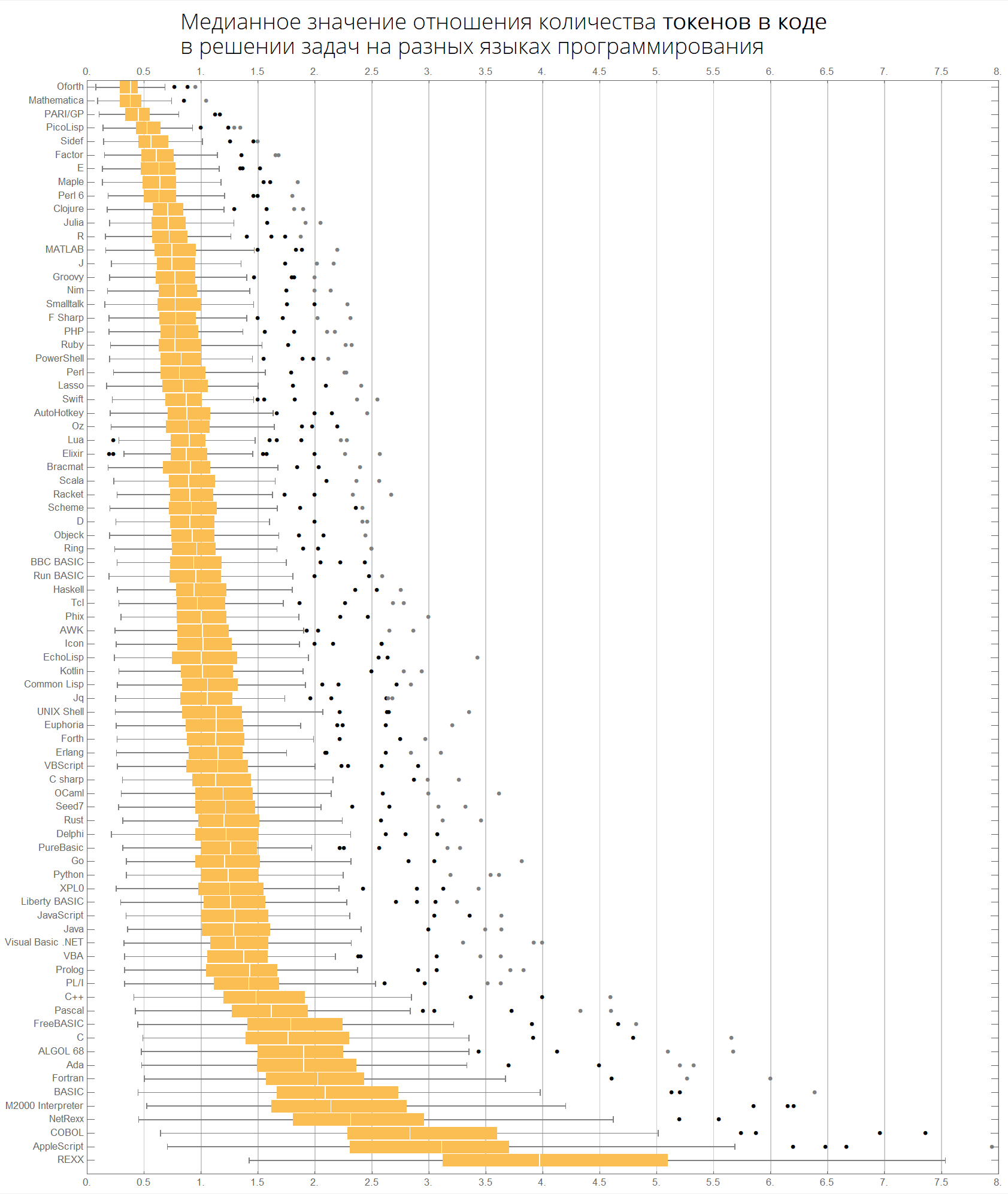
Vamos ver quais tokens são populares em diferentes idiomas:
languagePopularTokens[lang_, nMin_:50]:=Framed[Labeled[Style[Row[{" ", Style[lang, Bold]}], FontFamily->"Open Sans Light", 24], WordCloud[Cases[SortBy[Tally[Flatten[Values[langData[lang][["tokens"]]]]], -Last[#]&], {x_/; (StringLength[x]>1&&StringMatchQ[x, RegularExpression["[a-zA-Z0-9.]+"]]&&Not[StringMatchQ[x, RegularExpression["[0-9.]+"]]]), y_/; y>nMin}], ImageSize->{1000, 500}, MaxItems->200, WordOrientation->{
clouds=Grid[{Image[#, ImageSize->All]&@Rasterize[languagePopularTokens[#, 10]]}&/@{"Mathematica", "C", "Python", "Go", "JavaScript"}]

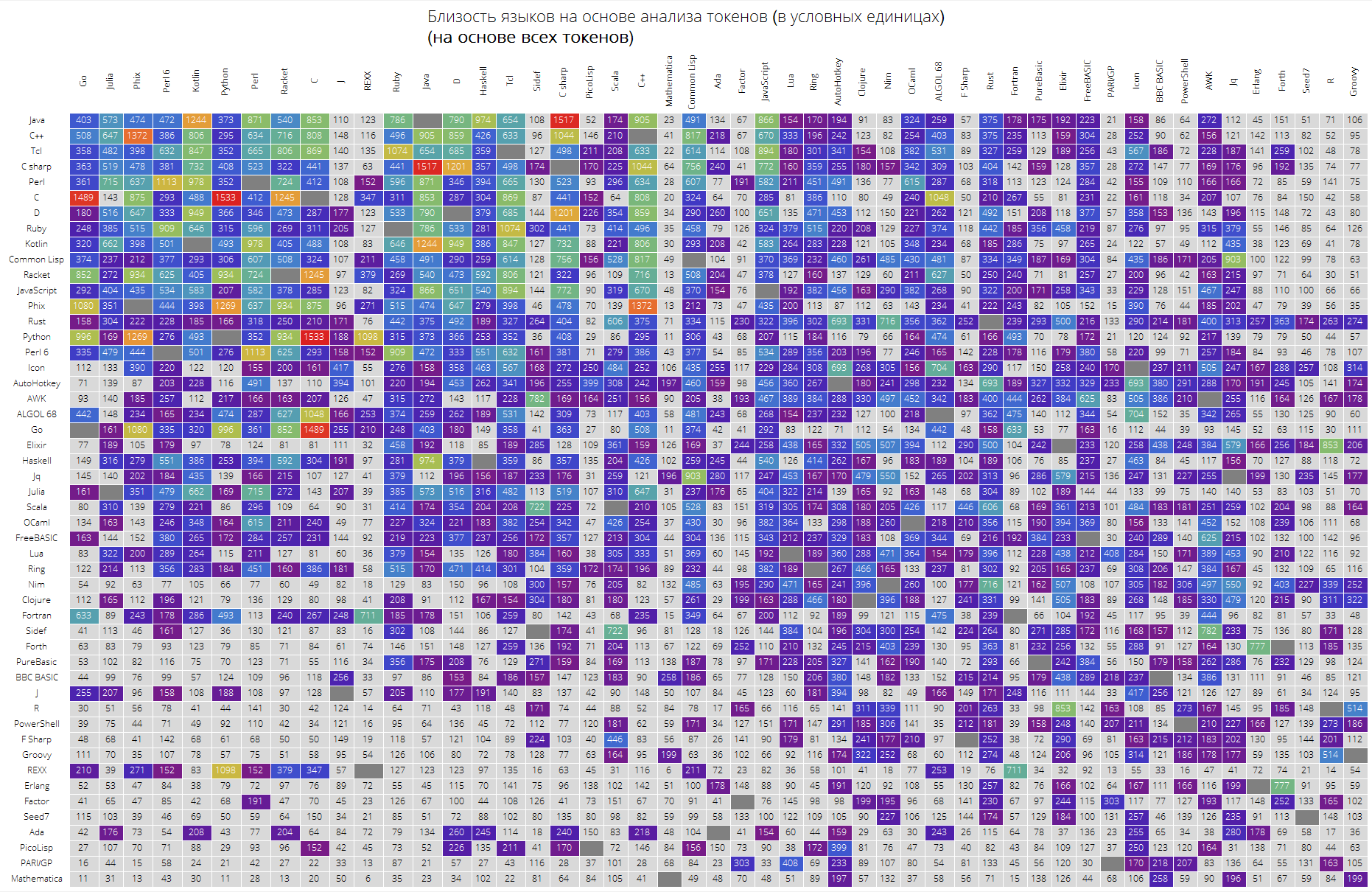
E, finalmente, uma comparação muito interessante de idiomas com base na proximidade de seus tokens.
A função langSimilarity funciona da seguinte maneira: primeiro, “tokens significativos” são selecionados (aqueles que são considerados todas as cadeias de caracteres latinos com um comprimento de pelo menos 2 caracteres que podem conter um ponto); os tokens são pesquisados em um par de idiomas lang1 e lang2; depois disso, considera-se a medida de sua “similaridade”, como o produto da medida Jacquard de dois conjuntos de fichas pela quantidade responsável pela proximidade das fichas entre si (a soma dos elementos da forma
onde
É a soma das aparências de token em todas as soluções para problemas de idioma lang1 e lang2, respectivamente).
Clear[langSimilarity]; langSimilarity[{lang1_,lang2_},clearTokens_]:=langSimilarity@@(Sort[{lang1,lang2}]~Join~{clearTokens}); langSimilarity[lang1_,lang2_,clearTokens_:False]:=langSimilarity[lang1,lang2,clearTokens]=Module[{tokens,t1,t2,t1W,t2W,intersection}, tokens[lang_]:=Module[{values,tokensPre,allValues,replacements,n}, values=Values[langData[lang][["tokens"]]]; n=Length[values]; allValues=DeleteDuplicates[Flatten[values]]; tokensPre=If[clearTokens,Cases[allValues,x_/;(StringLength[x]>1&&StringMatchQ[x,RegularExpression["[a-zA-Z0-9._$]+"]]&&Not[StringMatchQ[x,RegularExpression["[0-9.,eE]+"]]])],allValues]; replacements=Dispatch@ Thread[Complement[allValues,tokensPre]->Nothing]; Cases[Tally@Flatten@(values/.replacements),{t_,x_/;x>=n/10}:>{t,x}]]; {t1,t2}=tokens/@{lang1,lang2}; {t1W,t2W}=Dispatch/@{Rule@@@t1,Rule@@@t2}; intersection=Intersection[t1[[;;,1]],t2[[;;,1]]]; Times@@{Total[(#[[1]]+#[[2]])/(1+Abs[#[[1]]-#[[2]]])&/@Transpose@N[{intersection/.t1W,intersection/.t2W}]],Length[intersection]/Length[Union[t1[[;;,1]],t2[[;;,1]]]]}]
ClearAll[langSimilarityGrid]; langSimilarityGrid[n_Integer, OptionsPattern[{"SortQ" -> True, "measureFunction" -> Mean, "clearTokens" -> True}]] := Module[{$nPL, $pl, tableData, notSortedTableData, order, fullTableData, min, max, orderedMeans, median, rescale}, $nPL = n; $pl = $popularLanguages[$nPL][[;; , 1]]; tableData = Quiet@Table[ If[i == j, "", langSimilarity[{$pl[[i]], $pl[[j]]}, OptionValue["clearTokens"]]], {i, 1, $nPL}, {j, 1, $nPL}]; {min, max} = MinMax[Flatten[tableData] /. "" -> Nothing]; median = 10^Median@Log10@Flatten[tableData /. "" -> Nothing]; rescale = Function[Evaluate[Rescale[#, {median, max}, {0, 1}]]]; order = If[OptionValue["SortQ"], Ordering[tableData, All, OptionValue["measureFunction"][#1 /. "" -> Nothing] > OptionValue["measureFunction"][#2 /. "" -> Nothing] &], Range[1, $nPL]]; fullTableData = Transpose[{{""}~Join~$pl[[order]]}~Join~ Transpose[{Map[Rotate[#, 90 Degree] &, $pl]}~Join~ ReplaceAll[tableData[[order]], x_?NumericQ :> Item[Style[Round[x, 1], If[x < median, Black, White]], Background -> If[x < median, LightGray, ColorData["Rainbow"][rescale[x]]]]] /. "" -> Item["", Background -> Gray]]]; Framed[ Labeled[Style[ Row[{" ( )", "\n", "(", Style[If[OptionValue["clearTokens"], " ", " "], Bold], ")"}], 22, FontFamily -> "Open Sans Light", TextAlignment -> Center], Grid[fullTableData, Background -> White, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], Dividers -> White]], FrameStyle -> None, Background -> White]];
UPD: após um comentário valioso, a assembléia decidiu fazer duas tabelas: com fichas limpas e com todas as fichas, sem qualquer tipo de limpeza, a fim de influenciar o resultado o mínimo possível. O resultado é um pouco diferente, como você pode ver por si mesmo, embora algumas dependências tenham se tornado mais claras.
Aqui está o que obtemos (tabela não classificada):
langSimilarityGrid[30, "SortQ" -> False, "clearTokens" -> True] langSimilarityGrid[30, "SortQ" -> False, "clearTokens" -> False]
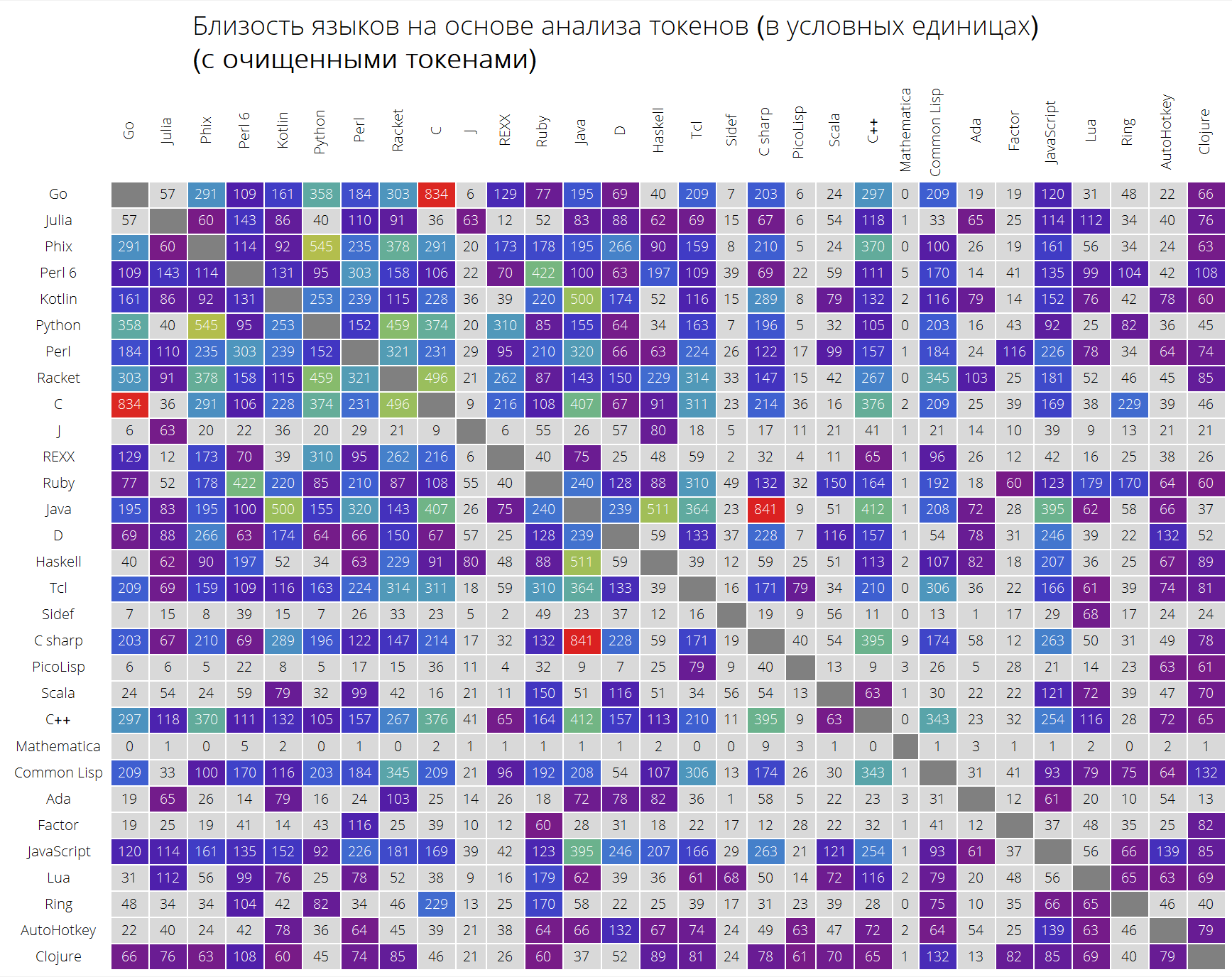

Tabela classificada (em termos de similaridade média com outras linguagens - quanto maior a linha, maior o número de outras linguagens de programação com essa linguagem):
langSimilarityGrid[30, "SortQ"->True, "clearTokens" -> True] langSimilarityGrid[30, "SortQ"->True, "clearTokens" -> False]


Por fim, uma tabela grande para os 50 primeiros idiomas em popularidade.
Espera-se que as linguagens "principais" como Java, C, C ++, C # estejam no topo. O Racket (anteriormente PLTScheme) estava lá, um dos objetivos é a criação, desenvolvimento e implementação de linguagens de programação.
Curiosamente, a Wolfram Language acabou sendo essencialmente uma linguagem diferente.
Os links entre as linguagens também são visíveis, digamos, o link entre Java e C #, Go e C, C e Java, Haskell e Java, Kotlin e Java, Python e Phix, Python e Racket e muito mais.
langSimilarityGrid[50, "SortQ"->True, "clearTokens" -> True] langSimilarityGrid[50, "SortQ"->True, "clearTokens" -> False]
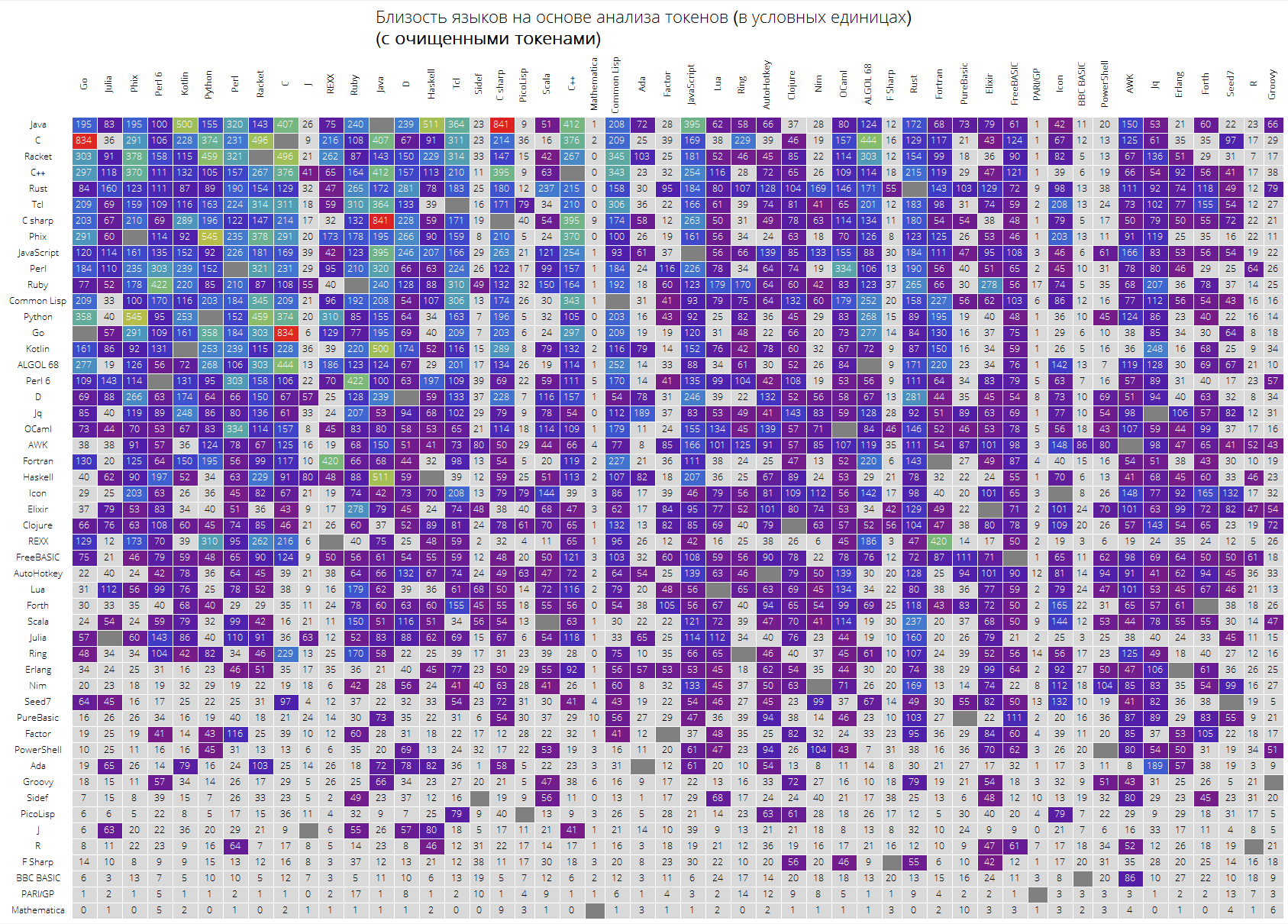
Espero que este estudo seja interessante para você e você possa descobrir algo novo. Para mim, como uma pessoa que constantemente usa a Wolfram Language, foi bom saber que ela é a linguagem mais “compacta”, por um lado, por outro lado, sua “dissimilaridade” objetiva com outras línguas, obviamente, dificulta a entrada nela.
Deseja aprender a programar no Wolfram Language?
Assista a seminários on- line semanais.
Inscrição para novos cursos . Curso online pronto.