Regressão linear e descida de gradiente

Que os indicadores X e Y, que possuem uma expressão quantitativa, sejam estudados em uma determinada área de assunto.

Além disso, há todos os motivos para acreditar que o indicador Y depende do indicador X. Essa posição pode ser uma hipótese científica e basear-se no senso comum elementar. Por exemplo, pegue supermercados.

Indicado por:

X - área de vendas (m²)

Y - faturamento anual (milhões de p.)

Obviamente, quanto maior a área de negociação, maior o volume de negócios anual (assumimos uma relação linear).

Imagine que temos dados sobre algumas n lojas (espaço de varejo e faturamento anual) - nosso conjunto de dados ek espaço de varejo (X), para o qual queremos prever o faturamento anual (Y) - nossa tarefa.

Nossa hipótese é que nosso valor de Y dependa de X na forma: Y = a + b * X

Para resolver nosso problema, devemos escolher os coeficientes a e b.

Primeiro, vamos definir valores aleatórios aeb. Depois disso, precisamos determinar a função de perda e o algoritmo de otimização.

Para fazer isso, podemos usar a função raiz quadrada de perda média ( MSELoss ). É calculado pela fórmula:



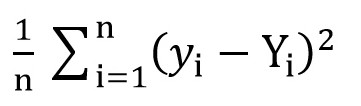
Onde y [i] = a + b * x [i] após a = rand () eb = rand () e Y [i] é o valor correto para x [i].
Nesta fase, temos o desvio padrão (uma certa função de aeb). E é óbvio que, quanto menor o valor dessa função, mais precisamente os parâmetros aeb são selecionados com relação aos parâmetros que descrevem a relação exata entre a área do espaço de varejo e a rotatividade nesta sala.

Agora podemos começar a usar a descida gradiente (apenas para minimizar a função de perda).

Descida de gradiente

Sua essência é muito simples. Por exemplo, temos uma função:

y = x*x + 4 * x + 3 

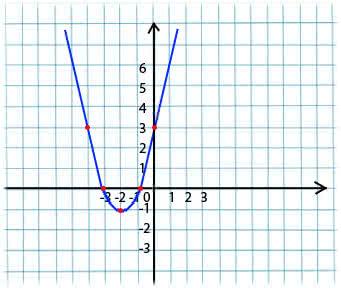
Tomamos um valor arbitrário de x do domínio de definição da função. Imagine que este é o ponto x1 = -4.

Em seguida, tomamos a derivada em relação a x dessa função no ponto x1 (se a função depende de várias variáveis ​​(por exemplo, aeb), precisamos tomar as derivadas parciais para cada uma das variáveis). y '(x1) = -4 <0

Agora temos um novo valor para x: x2 = x1 - lr * y '(x1). O parâmetro lr (taxa de aprendizado) permite definir o tamanho da etapa. Assim temos:

Se a derivada parcial em um determinado ponto x1 <0 (a função diminui), passamos para o ponto mínimo local. (x2 será maior que x1)

Se a derivada parcial em um determinado ponto x1> 0 (a função aumenta), ainda estamos nos movendo para o ponto mínimo local. (x2 será menor que x1)

Ao executar esse algoritmo iterativamente, abordaremos o mínimo (mas não o alcançamos).

Na prática, tudo isso parece muito mais simples (no entanto, não presumo dizer quais coeficientes aeb se encaixam com mais precisão com o caso acima com lojas, portanto, dependemos da forma y = 1 + 2 * x para gerar o conjunto de dados e, em seguida, treinamos nosso modelo. este conjunto de dados):
(O código está escrito aqui )

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

Após compilar o código, você pode ver que os valores iniciais de a e b estavam longe dos 1 e 2 necessários, respectivamente, e os valores finais estão muito próximos.

Esclarecerei um pouco por que a_grad e b_grad são considerados dessa maneira.
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) . A derivada parcial de F com relação a a será -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error . A derivada parcial de F com relação a b será -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error . Tomamos o valor médio (mean()) pois error e x_train e y_train são matrizes de valores, aeb são escalares.

Materiais utilizados no artigo:

directiondatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html