Geekly articles weekly

O número subjacente à música moderna


Por que doze?


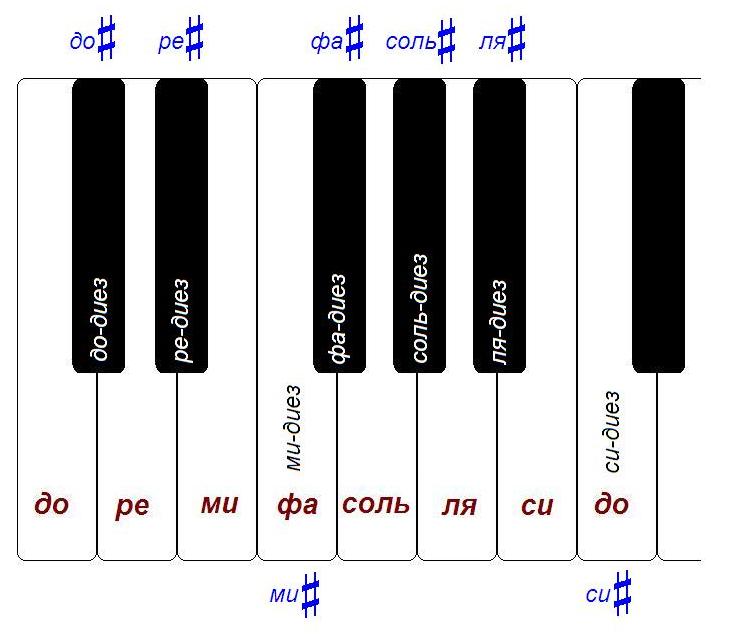
Se você olhar para o teclado, verá que cada oitava contém 12 semitons.
No caso do piano, isso significa apenas que, por exemplo, “para” a primeira oitava e “para” a segunda oitava, existem 11 teclas. Juntamente com um dos "do" (por exemplo, até a segunda oitava), temos 12 teclas: do #, re, re #, mi, fa, fa #, sal, sal #, la, la #, si, do.


Mas por que 12?


Talvez isso seja apenas um acidente? Nossos ancestrais gostaram do número 12, eles têm 12 em todos os lugares: 12 meses, 12 signos do zodíaco, 12 tribos de Israel, 12 apóstolos ... e aqui eles decidiram, que fossem 12, e assim foi ordenado. Ou ainda existe uma lei objetiva e esse número não é acidental?


Neste artigo, tentarei demonstrar que isso não é um acidente. Requisitos suficientemente gerais, bastante naturais para a música moderna (ocidental), com necessidade matemática, levam-nos ao número 12. É interessante que a razão pela qual temos esse valor seja propriedade de outro número (veja o final do artigo). Você pode até dizer que está no coração do som moderno.


Declaração do problema


Primeiro, vamos tentar formalizar a tarefa.


Temos uma frequência de referência $ \ omega_0 $ . Vamos chamá-lo de tônico. Temos também uma oitava com uma frequência $ 2 \ omega_0 $ . Agora precisamos entender quais opções para frequências intermediárias de $ \ omega_0 $ antes $ 2 \ omega_0 $ , para que uma melodia construída com essas notas soe harmoniosa para nossos ouvidos?


Receio que essa formulação, embora reflita a essência da pergunta, ainda seja, do ponto de vista matemático, bastante vaga, e essa pergunta não possa ser respondida sem ambiguidade, apenas porque a audição humana tem uma resolução de frequência bastante limitada. E isso é confirmado pelo fato de que em épocas diferentes foram usadas músicas diferentes, por exemplo, Pitágoras , músicas limpas , bem-temperadas e uniformemente temperadas . E todos soavam e soavam, pelo menos para certas obras, bastante aceitáveis.


O que é harmonia?


Devemos impor algumas condições adicionais. Mas primeiro, devemos responder a uma pergunta importante: o que percebemos como som harmonioso?


Vejamos dois sons - com frequências $ \ omega_1 $ e $ \ omega_2 $ .


Tome a proporção dessas frequências. Essa relação pode ser representada como um produto de números $ a_1 ^ {k_1} \ cdot a_2 ^ {k_2} \ cdot ... \ cdot a_l ^ {k_l} $ onde $ a_1, a_2, ..., a_l $ São números primos e $ k_1, k_2, ..., k_l $ - inteiros, por exemplo, essa relação pode ser igual a $ 2 ^ {- 3} \ cdot3 \ cdot5 $ . E que esses números primos ( $ a_1, a_2, ..., a_l $ ) menos, quanto mais harmonioso para o nosso ouvido esse intervalo soar (encontrei essa declaração aqui (consulte o segundo parágrafo) )


Assim, por exemplo, o som mais harmonioso de acordo com esta afirmação será uma oitava (mudança de frequência em 2 vezes). E os próximos intervalos harmônicos serão o quinto (mudança de frequência na $ 3/2 $ vezes) e um quarto (mudança de frequência $ 4/3 $ vezes).


Mas não é tão simples com esta afirmação. Assim, por exemplo, não está muito claro como o grau afeta. Por exemplo, o que é multiplicação mais harmoniosa por $ 3 ^ 2 $ ou 7? Não sei se esta questão foi estudada ou não e é possível, em princípio, dar uma resposta para ela. Além disso, a percepção da harmonia é uma coisa bastante subjetiva. Então, a música moderna está cheia de sons que seriam percebidos como uma terrível cacofonia por 100 a 200 anos.


A primeira condição. Tônico, Quart, Quint, Oitava


Essa incerteza não é um problema para nossa pequena pesquisa. O fato é que a única conclusão que quero tirar dessa afirmação é que, em nosso caso, em qualquer caso, deve haver pelo menos os intervalos "mais harmoniosos", a saber, uma oitava, um quarto e um quinto. Ou seja, junto com o tônico com uma frequência $ \ omega_0 $ e oitava com uma frequência $ 2 \ omega_0 $ devemos também ter um quinto e um quarto, com frequências respectivamente $ {3 \ over 2} \ omega_0 $ , $ {4 \ over 3} \ omega_0 $ ou algo muito próximo que não conseguimos distinguir de um quinto e quarto puros.


Nota: de fato, apenas tônicos, quintos e oitavas são suficientes. A presença de um quinto está imediatamente nos dando um quart, como adição a uma oitava, e em virtude da segunda condição (invariância), descrita abaixo, também devemos ter um quart e um tônico. Ou seja, a necessidade de um quarto é uma consequência da presença de um quinto e da exigência de invariância.


E este é o nosso primeiro requisito.


A segunda condição. Invariância


Nosso segundo requisito é invariância. E este é um requisito importante da música moderna. Este requisito consiste no fato de que todas as harmonias em qualquer tecla devem soar iguais. Se estamos falando do sistema moderno, que é usado para afinar o piano, isso significa que o quinto, composto por sete semitons, deve soar o mesmo, independentemente de qual som ele é construído. Ou seja, a taxa de frequência entre fazer e sal deve ser a mesma que para fazer # - salt #, re - la, re # - la #, ... e igual $ 3/2 $ . E essa invariância deve se aplicar, é claro, não apenas ao quinto, mas também a quaisquer intervalos. Uma vantagem importante desse sistema é a capacidade de transpor a peça a qualquer intervalo. Essa é a essência do temperamento uniforme.


Devo dizer que esse requisito de invariância não é tão óbvio, e essa abordagem foi aplicada relativamente recentemente, apenas no século XVIII. Os sistemas usados ​​anteriormente (por exemplo, Pitágoras e puro) não possuíam essa propriedade. Por exemplo, ouça a Sonata para piano microtonal (Ben Johnston) , escrita em um sistema limpo (limite primo = 5). Parece que o piano não está afinado. Toda a riqueza das harmonias modernas se baseia precisamente nessa invariância. Por exemplo, o "cravo bem temperado" de Bach apareceu precisamente graças a uma nova abordagem para ajustar os teclados. Foi essa invariância que permitiu a Bach criar sequências harmônicas que eram simplesmente impossíveis antes.


Então, agora temos todos os dados necessários para o cálculo.


Cálculo


Vamos construir uma escala de tônicos a oitavas que atenda aos dois requisitos.
Suponha que, neste caso, tenhamos $ N $ sons (incluindo uma oitava). É $ N $ e é o número desejado. Queremos mostrar que $ N $ sob nossas condições deve ser 12.


Uma conseqüência do segundo requisito é que o intervalo entre as frequências dos sons vizinhos seja o mesmo e igual $ 2 ^ {1 \ over N} $ .


Agora, o primeiro requisito diz que em nossa linha deve haver dois sons correspondentes às frequências (com uma boa aproximação) $ {3 \ over 2} \ omega_0 $ e $ {4 \ over3} \ omega_0 $ . Este é o quinto e quarto. Suponha que um quarto é $ n_1 $ som em nossa linha, e o quinto - $ n_2 $ ah Nós denotamos $ n = n_2 - n_1 $ .


É fácil ver que a mudança na frequência entre o quarto e o quinto (taxa de frequência) é $ 9/8 $ .


Mas, de acordo com nossa segunda condição, isso também deve ser igual $ 2 ^ {n \ sobre N} $ .


Então, nós temos a fórmula:


$ 2 ^ {n \ over N} \ aproximadamente 9/8 $


Após transformações simples, obtemos a fórmula básica:


$ n \ aproximadamente N (2 \ log_2 {3} - 3) = N \ cdot 0,170 $


É fácil ver que a solução (é claro, aproximada) é $ N = 6i $ onde $ i $ - qualquer número naturalmente (pequeno o suficiente, porque, no entanto, 0,170 difere de 1/6).


Vamos olhar para um caso $ i = 1 $ . Neste caso $ N = 6 $ , $ n = 1 $ . Ou seja, essa é uma variante do sistema moderno, apenas sem meios-tons, apenas com tons (do, re, mi, fa #, salt #, la #, do). Mas, como você pode ver, nesse caso o quart (f) e o quint (sal) não se enquadram nessa escala.


Ou seja, a única opção para nós pode ser


$ N = 12 i $ onde $ i $ - qualquer número natural ( $ i $ pequeno o suficiente). Case $ i = 1 $ corresponde apenas ao nosso sistema moderno, chamado sistema uniformemente temperamental.


Mas por que não 24 ou mais? O motivo é simples - posso assumir que essa graduação já é excessiva para nossa percepção. Portanto, apenas um número permanece: 12.


Se você não estiver satisfeito com a linha de pensamento, aqui você pode encontrar


prova matemática rigorosa

Desafio:


Encontre o número inteiro positivo mínimo N no qual existe um número inteiro positivo $ n <N $ tal que $ 2 ^ {n \ sobre N} $ diferente de $ 3 \ mais2 $ não mais que $ \ delta $ centavos .


Solução:


Denotar por $ Z_n = N \ cdot (log_2 {3} -1) $ . Então, com $ \ delta <{1200 \ over N} $ (o que é verdade para o intervalo daqueles $ \ delta $ e $ N $ que consideraremos) nossa tarefa é encontrar o mínimo $ N $ em que


$ {1200 \ sobre N} \ cdot | Z_n - redondo (Z_n) | <\ delta $ ,


onde $ rodada $ - função de arredondamento para o número inteiro mais próximo.


Vamos resolver esse problema numericamente.


imagem


Agora é hora de decidir $ \ delta $ .


Que quantidade (em centavos) da discrepância entre o quinto puro e o “nosso quinto” consideramos aceitável? Muitas pessoas ouvem, por exemplo, que o terço grande / pequeno do sistema uniformemente temperado "finge". Mas isso é apenas cerca de 15 centavos em relação a intervalos puros. Portanto, nossa exigência deve ser superior a 15 centavos. Algumas fontes dizem que, em determinadas frequências, os músicos distinguem de 5 a 6 centavos. Portanto, é sábio tomar $ \ delta = 5 $ .


Então a tabela mostra claramente que o menor $ N = 12 $ . Os seguintes são satisfatórios $ N = 17,24,29,34,36,41, ... $ .


Nota:
Próxima iteração, para cada $ N $ você também precisa verificar o som e outros intervalos. Em caso de $ N = 17 $ por exemplo, terços se tornam completamente "falsos": mais de 30 centavos (para um terço grande).


Portanto, nossa resposta é: $ N = 12 $ . O que era necessário para provar.


E, a propósito, é claro que nossa resposta não mudará se, em vez disso, $ \ delta = 5 $ tome, por exemplo, 10 ou até 15.


Conclusão Número subjacente


Surpreendentemente, verifica-se que o número subjacente ao sistema musical moderno e à música contemporânea (européia) é $ \ log_2 {3} $ , ou seja, que com boa precisão (0,1%) a seguinte igualdade é válida:


$ \ log_2 {3} \ aproximadamente 19/12 $


Respostas a comentários e críticas nos comentários

Primeiro de tudo, obrigado pelos comentários interessantes!
Aqui estão minhas respostas para os comentários e críticas mais importantes (na minha opinião).


Crítica 1. Ovo ou galinha


Druu: Olha, 12 sons em uma oitava atingiram um temperamento uniforme em geral, então você não pode justificar 12 sons com a ajuda do temperamento, isso será simplesmente falso.


covil: Essa é exatamente a lógica do anel que estou falando: se você escolher músicas criadas em um sistema específico, é óbvio que, em seu contexto, um sistema diferente é impossível.


Para essas e outras observações semelhantes, cito 2 contra-argumentos:


1) se com precisão suficiente a igualdade $ log_2 {3} = 19/12 $ , seria impossível "puxar" um sistema de temperamento uniforme para um sistema puro composto por 12 sons. Quanto mais forte $ log_2 {3} $ diferente de $ 19/12 $ , mais falso nosso quinto soaria. Se esse número fosse (fortemente) diferente, não haveria uma abordagem temperamental uniformemente para intervalos puros e, como resultado, não haveria música moderna ou, digamos, seria diferente. Portanto, a conclusão de que as propriedades do número é bastante lógica $ log_2 {3} $ são a base da música moderna.


2) o segundo contra-argumento é impossível de justificar logicamente, e é apenas uma suposição, mas parece-me que todo esse raciocínio é digno de atenção. Vamos tentar responder à pergunta: por que surgiu a necessidade de um sistema uniformemente temperado? Os comentários já responderam parcialmente. A música da época (a época da criação de um sistema uniformemente temperamental) já usava modulações e polifonia, que de fato, em geral, já exigiam temperamento uniforme. O problema do som "falso" foi resolvido pelo fato de os músicos "ajustarem" levemente o som durante a apresentação. Era fácil fazer cordas (pelo menos irritadas), ventos e vocais (correto, se eu estiver errado - eu concluí com seus comentários). Por exemplo, para o violino - esta é apenas uma ligeira mudança na posição dos dedos. Mas assim que você foi privado dessa oportunidade (cravo), imediatamente tudo começou a parecer ruim. Então, parece que essas 12 notas apareceram não apenas assim, mas como um desenvolvimento natural da música em direção a essa possibilidade de modulações livres e polifonia rica, e isso, por sua vez, é uma consequência da invariância. Foi um desenvolvimento natural da música. Ou seja, quero dizer que se a invariância matematicamente fosse possível não para 12 sons, mas, por exemplo, para 10, então (mesmo antes do temperamento uniforme) em nossa escala teríamos 10 sons (neste caso, estou falando sobre o caminho desenvolvimento da música europeia). E então 10 sons de temperamento uniforme seriam atraídos para o nosso sistema puro.


Crítica 2. A singularidade dos doze


Houve muitas críticas sobre a afirmação de que 12 é o único número razoável.


Primeiro, entendendo a agressividade dessa afirmação e o princípio da impossibilidade de uma justificação rigorosa, reduzi possivelmente o grau de categorização de algumas das alegações contidas no artigo. E ainda ...


Nesse caso, temos duas linhas de crítica.


1) Por que considero 19, 24 ou 29 (etc.) inaceitável?


Não, acho que não. Para diferentes instrumentos, existem técnicas para usar sons fora da escala, por exemplo, glissando e vibrato. Essas técnicas acrescentam beleza e naturalidade ao som. Portanto, mesmo com 12 notas, ainda usamos sons auxiliares. Se estamos falando de ambientes, de sons incomuns, de enriquecer o som ... isso é bastante justificado, mas se estamos falando de tons básicos, tenho dúvidas. A música é criada não apenas para a elite, mas para as pessoas comuns, e para elas essa graduação (IMHO) é desnecessária.


O segundo argumento, e foi apresentado nos comentários, é, de fato, a complexidade de criar instrumentos e desempenho no caso de uma escala longa, embora tenhamos um ótimo exemplo de tal instrumento - cítara. Mas tente fazer uma oitava (com uma mão) no piano se você tiver uma escala de 24 sons.


2) Mas e o pentatônico?


Em todos os países do leste em que eu estava, por algum motivo, raramente ouvia música nacional construída na escala pentatônica. E todos os músicos do leste, a quem ouvi (e amo alguns), também tocaram bastante música européia. Aqui está uma citação interessante: "Os compositores acadêmicos usam o pentatônico como tinta especial desde o século 19 para dar à música um sabor arcaico". O aroma do arcaico ...
No entanto, na minha percepção, essa música não é moderna, mas não quero defender essa posição; portanto, em alguns lugares do artigo, uso o termo "música européia moderna". É claro que essa música (construída na escala pentatônica) se desenvolveu de acordo com outras leis e não alcançou a demanda por polifonia rica e modulação frequente e fácil, que apareceu na música européia. Portanto, este artigo obviamente não é sobre pentatônico.


Crítica 3. Música contemporânea


Como chamo música moderna?


Embora isso pareça uma tautologia, por música moderna quero dizer música que requer invariância, que no caso de instrumentos com um sistema fixo (por exemplo, cravo, piano) leva à necessidade de um sistema uniformemente temperado (ou algo próximo). No caso de outros instrumentos, por exemplo, cordas sem trastes, tudo parece um pouco mais complicado, porque, na realidade, é possível usar um conjunto de sons maior que (12). Mas ainda assim, quando falamos sobre a exigência de invariância, queremos dizer que esses sons devem estar muito próximos (em frequência) aos nossos 12.


Essa definição inclui quase toda a música de piano, clássica européia, jazz, rock, pop e todos os seus derivados. Estou certo de que existem exceções, mas IMHO essas são as exceções. Não vejo motivo para discutir isso, porque todos podem investir algo nesse conceito.


Crítica 4. Cálculo


Erro nos cálculos.


Eu acho que essa pergunta foi removida. No entanto, devo admitir que, no decorrer da discussão, fiz várias declarações errôneas sobre coisas secundárias que não afetaram a conclusão principal do artigo.


PS Não trate este artigo (e faça os requisitos correspondentes) como um trabalho acadêmico. :) Este não é um artigo sobre teoria musical. Além disso, este não é um artigo sobre a história da música. Nessas áreas, de maneira alguma considero meu conhecimento pelo menos significativo e admito que possa haver imprecisões, embora tenha tentado evitá-las. Aqui é formulado um simples problema matemático (de nível de complexidade escolar), cuja solução, como me pareceu, tem uma interpretação interessante. Com o qual eu compartilhei.

Source: https://habr.com/ru/post/pt471600/

More articles:


All Articles