Amor de matemática

Baseado em um artigo de Julien Clinton Sprott. Modelos dinâmicos de amor. Psicologia Dinâmica Não Linear e Ciências da Vida, agosto de 2004.

Eu acreditava que a harmonia na álgebra ...
A teoria do meu amigo é seca, mas a árvore da vida é sempre verde ...

Quem simplesmente não brigou com esse "problema" .... Foi desmantelado em tragédias gregas antigas, o grande Shakespeare nos contou a história de Romeu e Julieta, Andrzej Wajda desmontou-o de ambos os lados na Anatomia do Amor. Mas as pessoas nunca chegaram ao fundo da verdade até os cientistas tomarem a decisão. É verdade que nem tudo parece convincente para os psicólogos. Às vezes eles mesmos, mesmo depois do divórcio, começam a analisar a história do amor que partiram. Bem, escreva livros que às vezes parecem bolos quentes. Eles são escritos por especialistas! O que posso dizer? Quase nada pessoal - apenas negócios ...

E, finalmente, não poetas com escritores e psicólogos se apaixonaram pela garganta. A matemática é a rainha das ciências. Ela é capaz de lidar com um problema eterno? Os livros são publicados, por exemplo, por John Gotman, "The Mathematics of Marriage", e outros autores. Os matemáticos consideram o desenvolvimento de relacionamentos românticos como um processo dinâmico ...

E tudo começa, como esperado, com definições. Como identificar o amor qualitativa e quantitativamente? Os pesquisadores classificam o problema por tipo: caso de amor, paixão, fidelidade. Além disso, cada espécie tem um conjunto complexo de sentimentos. Mas, além do amor por outra pessoa, existe amor por si mesmo, pela vida, pela humanidade ...

Ao mesmo tempo, o oposto do amor - no modelo matemático - não pode ser odiado, pois esses dois sentimentos podem coexistir ao mesmo tempo. Por exemplo, alguém pode gostar de algumas manifestações de um parceiro, mas outras podem ser desagradáveis. Portanto, não é realista supor que o amor de um indivíduo seja influenciado apenas por seus próprios sentimentos, e os sentimentos do outro parceiro não dependam de outras influências, e que os parâmetros que caracterizam a interação de duas pessoas permaneçam inalterados e, portanto, excluem a possibilidade de aprendizado e adaptação.

A complexidade, mesmo em um modelo restrito mínimo, aumenta dramaticamente quando três ou mais variáveis ​​são introduzidas nas equações de não linearidade e / ou.

* Nota: tradutor. Na minha opinião, esses estudos também podem reviver a própria matemática, atrair a atenção do público, geralmente distante dessa ciência abstrata.

Modelo linear simples

A história de amor de Romeu e Julieta no tempo (t) pode ser representada usando as funções * R (t) - o amor de Romeu por Julieta e J (t) - o amor de Julieta por Romeu.

Então, um modelo linear simples de sua relação é expresso pelas equações (1)



aeb - parâmetros do estilo romântico de Romeu
ce - opções de estilo Julieta
a - caracteriza como Romeu está envolvido em seus próprios sentimentos
b - quanto Romeu é abraçado pelos sentimentos de Julieta

Um dos artigos (Gottman et al., 2002) utiliza o termo “inércia comportamental” para o primeiro e a “função de influência” para o segundo parâmetro. Embora em a = 0, a inércia se torne maior. O modelo dinâmico sob tais condições é bidimensional e controlável pelas condições iniciais e quatro parâmetros, que podem ser positivos ou negativos.

Um modelo linear simples foi proposto por Rinaldi, 1998a. Ao mesmo tempo, é adicionado um termo livre a cada derivado, a fim de levar em consideração a atratividade (ou antipatia com valor negativo), que cada um dos parceiros mostra ao outro na ausência de outros sentimentos. Esse modelo é mais realista porque permite que os sentimentos cresçam a partir de um estado de indiferença e fornece um equilíbrio que não é caracterizado por apatia completa. Tudo isso é descrito dessa maneira apenas inserindo dois parâmetros adicionais. Embora o estado de equilíbrio não apático possa ser muito importante para os indivíduos em questão, isso não altera a dinâmica senão movendo o espaço de estados RJ.

Estilos românticos

Romeu pode exibir um dos quatro estilos românticos, dependendo dos sinais aeb, com a notação dada pelo autor da obra (Strogatz, 1994) e seus alunos:

1. Desejo apaixonado: a> 0, b> 0 (Romeu está envolvido nos sentimentos e sentimentos de Julieta.)
2. Tipo narcisista: a> 0, b <0 (Romeu é mais envolvido em seus próprios sentimentos, ele se distancia dos sentimentos de Julieta.)
3. Cauteloso (ou amante confiável): a <0, b> 0 (Romeu se afasta de seus próprios sentimentos, mas é dominado pelos sentimentos de Julieta.)
4. Eremita: a <0, b <0 (Romeu é separado dos sentimentos e sentimentos de Julieta.)

Como quatro estilos de comportamento também são possíveis para Julieta, existem 16 combinações possíveis de pares, cada um com sua própria dinâmica, embora metade deles corresponda a uma permutação de R e J.

As equações (1) determinam um único ponto de equilíbrio para R = J = 0, que corresponde a uma relação mutuamente indiferente, ou o chamado "platô do amor" (no modelo de Rinaldi, 1988), com uma descrição do comportamento através de valores próprios (2)




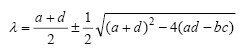
Focus Forking Saddle
Fig. 1. A situação dinâmica próxima ao ponto de equilíbrio no espaço bidimensional, de acordo com a equação 1.

Triângulo do amor

Um modelo mais matematicamente rico é obtido quando uma terceira pessoa é adicionada a um modelo simples, principalmente porque é possível que se formem alianças nas quais dois indivíduos possam se unir contra o terceiro. Suponha que Romeu tenha outro amante, Genevieve, embora a terceira pessoa em questão possa ser uma criança ou outro parente. Nesse caso, o espaço dos estados se torna mais provável em seis dimensões do que em duas dimensões, uma vez que cada um dos três tem sentimentos pelos outros dois e surgem doze parâmetros se cada um puder assumir estilos diferentes em relação ao outro, mesmo que a atração natural seja ignorada ( revisado por Rinaldi, 1998a).

No caso mais simples, Julieta e Genevieve podem não conhecer a existência um do outro, e Romeu pode mostrar o mesmo estilo romântico em relação a ambos. O sistema quadridimensional resultante é então transformado em dois sistemas bidimensionais divididos, até que os sentimentos de Romeu por Julieta sejam de alguma forma influenciados pelos sentimentos de Genevieve por ele, e o mesmo se aplica a Genevieve.

Efeitos não lineares

Há um número infinito de maneiras de inserir efeitos não lineares. Imagine que Romeu responda positivamente ao amor de Julieta, mas com uma manifestação excessiva do amor dela, ele se sente estrangulado e exibe uma reação adversa. Por outro lado, se Julieta mostra antipatia suficiente, Romeu pode tentar se tornar agradável para ela.

Nesse caso, é possível substituir bJ na equação 1 pela função logística bJ (1 - | J |) correspondente à medida de J em unidades, desde que J = 1 corresponda ao valor em que seu amor se torna contraproducente. Resultados qualitativamente semelhantes seguem a função bJ (1 - J2), que é o caso considerado por Rinaldi (1998b) para o poeta italiano do século XIV, modelo de amor platônico pela bela Laura, vinculado pelo casamento. Assumindo o mesmo para Juliet, obtemos:
4)



Existem 4 estados de equilíbrio, incluindo um na origem. A Figura 3 mostra o foco constante no qual Juliet. como “desejos apaixonados” (c = d = 1) leva o “eremita” de Romeu (a = b = –2) a um estado de amor mútuo em R = J = 2. Um modelo semelhante para amantes cautelosos (confiáveis) com não-linearidade sigmoidal também leva a equilíbrio estável (Rinaldi e Gragnani 1998). As equações 4 obviamente não permitem ciclos limite, e o caos não ocorre enquanto o sistema é bidimensional.


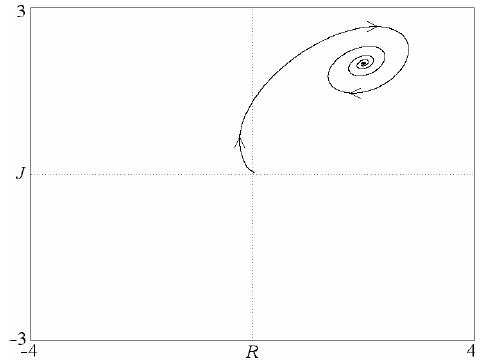Fig. 3. Uma das soluções para o modelo não linear de acordo com a equação 4.

Talvez a aplicação de efeitos não lineares a triângulos de amor.

Posfácio

Alguns dos modelos dinâmicos lineares do amor exibem dinâmicas surpreendentemente complexas, enquanto muitos deles parecem ser semelhantes à experiência conhecida nos relacionamentos. Se houver três ou mais variáveis ​​e até os efeitos não-lineares mais simples forem introduzidos, o caos poderá ocorrer. Uma extensão interessante do modelo pode ser imaginada quando se considera um grupo de personalidades em interação, por exemplo, para casos de uma família grande ou comunidade. Tais modelos, é claro, são muito simplificados, uma vez que o amor é levado em consideração como uma variável escalar simples, e as reações dos indivíduos em relação ao seu próprio amor e o amor de outras personalidades por eles são consistentes e mecanicistas, sem levar em consideração fatores de influência externos.

PS O amor pode viver sem a matemática, mas a matemática evoca o amor de si por pessoas que valorizam a verdadeira harmonia.

Referências:
Julien Clinton Sprott. Modelos dinâmicos de amor. Psicologia da Dinâmica Não Linear e Ciências da Vida • Agosto de 2004

Rinaldi, S. (1998a). Dinâmica do amor: o caso de casais lineares. Matemática Aplicada e Computação, 95, 181-192.
Rinaldi, S. & Gragnani, A. (1998). Dinâmica do amor entre indivíduos seguros: uma abordagem de modelagem. Dinâmica não-linear, psicologia e ciências da vida, 2, 283-301.
Rinaldi, S. (1998b). Laura e Petrarch: Um caso intrigante da dinâmica cíclica do amor. Jornal SIAM sobre Matemática Aplicada, 58, 1205-1221