Inferência Variacional - o que é e o que come?

Olá Habr!

Recentemente, conversei com colegas sobre um codificador automático variacional, e muitos até os que trabalham no Deep Learning sabem sobre a inferência variacional (inferência variacional) e, em particular, o limite variacional inferior apenas por boatos e não entendem completamente o que é.
Neste artigo, quero analisar esses problemas em detalhes. Quem se importa, peço um recorte - será muito interessante.

O que é inferência variacional?

A família de métodos variacionais de aprendizado de máquina recebeu esse nome na seção de análise matemática "Cálculo variacional". Nesta seção, estudamos os problemas de pesquisa de extremos de funcionais (um funcional é uma função de funções - ou seja, não estamos procurando os valores de variáveis ​​nas quais a função atinge seu máximo (mínimo), mas uma função na qual o funcional atinge um máximo (mínimo).

Mas surge a pergunta - no aprendizado de máquina, sempre procuramos um ponto no espaço de parâmetros (variáveis) no qual a função de perda tem um valor mínimo. Ou seja, é tarefa da análise matemática clássica, e aqui está o cálculo das variações? O cálculo das variações aparece no momento em que transformamos a função de perda em outra função de perda (geralmente esse é o limite variacional mais baixo) usando os métodos de cálculo de variações.

Por que precisamos disso? Não é possível otimizar diretamente a função de perda? Precisamos desses métodos quando é impossível obter diretamente uma estimativa de gradiente imparcial (ou essa estimativa tem uma dispersão muito alta). Por exemplo, nossos conjuntos de modelos $$$p (z)$ e $$$p (x / z)$ e precisamos calcular $$$p (x) = \ int (p (z) p (x / z) dz)$ . É exatamente para isso que o codificador automático variacional foi projetado.

Qual é o limite inferior variacional?

Imagine que temos uma função $$$f (x)$ . O limite inferior dessa função será qualquer função $$$g (x)$ satisfazendo a equação:

$$

$$g (x) <= f (x)$$

Ou seja, para qualquer função, existem inúmeros limites inferiores. Todos esses limites inferiores são iguais? Claro que não. Introduzimos outro conceito - discrepância (não encontrei um termo estabelecido na literatura em russo, esse valor é chamado de rigidez em artigos em inglês):

$$

$$\ delta = máximo {f (x)} - máximo {g (x)}$$

Obviamente, o residual é sempre positivo. Quanto menor o residual, melhor.

Aqui está um exemplo de um limite inferior com zero residual:

E aqui está um exemplo com um resíduo pequeno, mas positivo:

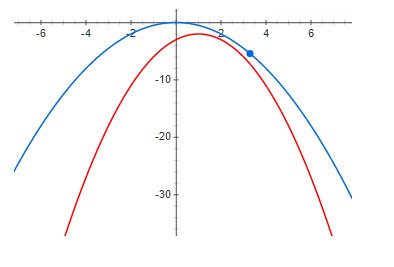
E, finalmente, uma discrepância grande o suficiente:


A partir dos gráficos acima, é claramente visto que, em zero residual, o máximo da função e o máximo do limite inferior estão no mesmo ponto. Ou seja, se queremos encontrar o máximo de alguma função, podemos procurar o máximo do limite inferior. Se a discrepância não for zero, não é assim. E o máximo do limite inferior pode estar muito distante (ao longo do eixo x) do máximo desejado. Os gráficos mostram que quanto maior o residual, maior a distância entre os altos. Isso geralmente não é verdade, mas na maioria dos casos práticos essa intuição funciona muito bem.

Codificador automático variável

Agora, analisaremos um exemplo de um limite variacional inferior muito bom com um resíduo potencialmente zero (abaixo ficará claro o porquê) - este é um Autoencoder variacional.

Nossa tarefa é construir um modelo generativo e treiná-lo usando o método de máxima verossimilhança. O modelo terá o seguinte formato:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

onde $$$q (x)$ É a densidade de probabilidade das amostras geradas, $$$z$ - variáveis ​​latentes, $$$q (z)$ - a densidade de probabilidade de uma variável latente (geralmente uma simples) - por exemplo, uma distribuição gaussiana multidimensional com expectativa zero e dispersão unitária - em geral, algo que podemos facilmente amostrar), $$$q_ \ theta (x | z)$ - densidade condicional da amostra para um dado valor de variáveis ​​latentes, no autoencoder variacional, é selecionado um gaussiano com expectativa e dispersão de esteira dependendo de z.

Por que precisamos representar a densidade de dados de uma maneira tão complexa? A resposta é simples - os dados têm uma função de densidade muito complexa e simplesmente não podemos tecnicamente construir diretamente um modelo dessa densidade. Esperamos que essa densidade complexa possa ser bem aproximada usando duas densidades mais simples. $$$q (z)$ e $$$q_ \ theta (x | z)$ .

Queremos maximizar a seguinte função:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

onde $$$p (x)$ - densidade de probabilidade dos dados. O principal problema é que a densidade $$$q (x)$ (com modelos suficientemente flexíveis) não é possível apresentar analiticamente e, consequentemente, treinar o modelo.

Usamos a fórmula de Bayes e reescrevemos nossa função da seguinte maneira:

$$

$$I = \ int {p (x) log (\ frac {q (z) q (x | z)} {q (z | x)}) dx}$$

Infelizmente $$$q (z / x)$ tudo também é difícil de calcular (é impossível obter a integral analiticamente). Mas, primeiro, observamos que a expressão sob o logaritmo não depende de z; portanto, podemos tirar a expectativa matemática do logaritmo em z de qualquer distribuição e isso não altera o valor da função e multiplica e divide pelo logaritmo na mesma distribuição (formalmente, temos apenas uma condição - essa distribuição não deve desaparecer em lugar nenhum). Como resultado, obtemos:

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {\ phi (z | x)} {q (z | x)})}}$$

note que, em primeiro lugar, o segundo termo é divergência de KL (o que significa que é sempre positivo):

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + \ int {p (x) KL [\ phi (z | x) || q (z | x))] dx}$$

e segundo $$$I$ não depende de $$$q (z | x)$ não de $$$\ phi (z | x)$ . Segue-se que,

$$

$$I> = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} = VLB$$

onde $$$Vlb$ - O limite variacional mais baixo (limite inferior variacional) e atinge seu máximo quando $$$KL [\ phi (z | x) || q (z | x))] = 0$ - ou seja, as distribuições são as mesmas.

Positividade e igualdade a zero se e somente se as distribuições coincidirem com divergências de KL são provadas precisamente por métodos variacionais - daí o nome limite variacional.

Quero observar que o uso de um limite inferior variacional oferece várias vantagens. Em primeiro lugar, nos dá a oportunidade de otimizar a função de perda por métodos gradientes (tente fazer isso quando a integral não for analisada analiticamente) e, em segundo lugar, aproxima a distribuição inversa $$$q (z | x)$ distribuição $$$\ phi (z | x)$ - ou seja, não podemos apenas amostrar dados, mas também amostrar variáveis ​​latentes. Infelizmente, a principal desvantagem é quando o modelo de distribuição inversa não é flexível, ou seja, quando a família $$$\ phi (z | x)$ não contém $$$q (z | x)$ - o resíduo será positivo e igual:

$$

$$\ delta = \ int {p (x) \ subconjunto {\ phi (z | x)} {min} (KL [\ phi (z | x) || q (z | x)]) dx}$$

e isso significa que o máximo do limite inferior e as funções de perda provavelmente não coincidem. A propósito, o codificador automático variacional usado para gerar imagens gera imagens muito embaçadas, acho que isso se deve apenas à escolha de uma família muito pobre $$$\ phi (z | x)$ .

Um exemplo de um limite inferior não muito bom

Agora vamos considerar um exemplo em que, por um lado, o limite inferior possui todas as boas propriedades (com um modelo suficientemente flexível, o residual será zero), mas, por sua vez, não oferece nenhuma vantagem sobre o uso da função de perda original. Acredito que este exemplo é muito revelador e, se você não fizer uma análise teórica, poderá gastar muito tempo tentando treinar modelos que não fazem sentido. Em vez disso, os modelos fazem sentido, mas se podemos treinar esse modelo, é mais fácil escolher $$$q (x)$ da mesma família e use diretamente o princípio da máxima verossimilhança.

Portanto, consideraremos exatamente o mesmo modelo generativo que no caso de um codificador automático variacional:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

treinaremos com o mesmo método de probabilidade máxima:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

Ainda esperamos que $$$q (x | z)$ Será muito "mais fácil" do que $$$q (x)$ .
Só agora vamos escrever $$$I$ um pouco diferente:

$$

$$I = \ int {p (x) log (\ int {q (z) q_ \ theta (x | z) dz}) dx}$$

usando a fórmula de Jensen, obtemos:

$$

$$I> = \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz} = VLB$$

É exatamente neste momento que a maioria das pessoas responde sem pensar que esse é realmente o ponto principal e você pode treinar o modelo. Isso é verdade, mas vamos olhar para a discrepância:

$$

$$\ delta = \ int {p (x) log (q (x)) dx} - \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz}$$

onde (aplicando a fórmula de Bayes duas vezes):

$$

$$\ delta = \ int {p (x) q (z) log (\ frac {q (x)} {q (x | z)}) dxdz} = \ int {p (x) q (z) log ( \ frac {q (z)} {q (z | x)}) dxdz}$$

é fácil ver que:

$$

$$\ delta = \ int {p (x) KL [q (z) || q (z | x)] dx}$$

Vamos ver o que acontece se aumentarmos o limite inferior - o residual diminuirá. Com um modelo bastante flexível:

$$

$$KL [q (z) || q (z | x)] \ rightarrow0$$

tudo parece estar bem - o limite inferior tem um resíduo potencialmente zero e com um modelo bastante flexível $$$q (x | z)$ tudo deve funcionar. Sim, isso é verdade, apenas leitores atentos podem perceber que zero resíduo é alcançado quando $$$x$ e $$$z$ são variáveis ​​aleatórias independentes !!! e para um bom resultado, a “complexidade” da distribuição $$$q (x | z)$ não deve ser inferior a $$$q (x)$ . Ou seja, a borda inferior não nos oferece vantagens.

Conclusões

O limite variacional mais baixo é uma excelente ferramenta matemática que permite otimizar aproximadamente funções “inconvenientes” para o aprendizado. Mas, como qualquer outra ferramenta, você precisa entender muito bem suas vantagens e desvantagens e também usá-la com muito cuidado. Consideramos um exemplo muito bom - um auto-codificador variacional, bem como um exemplo de um limite inferior não muito bom, enquanto os problemas desse limite inferior são difíceis de ver sem uma análise matemática detalhada.

Espero que tenha sido pelo menos um pouco útil e interessante.