Fórmula para calcular números primos e otimizar divisores de força bruta

Saudações! Decidi, à vontade, pesquisar o problema de encontrar números primos. O tópico é extenso e interessante. Quero compartilhar algumas idéias sobre isso que me vieram à mente. Uma pesquisa na Internet não revelou isso, apontando para sua originalidade.

Em primeiro lugar, nunca encontrei uma fórmula matemática para calcular os números primos em ordem. Afinal, se houver algoritmos, certamente é possível compor fórmulas usando funções ou operadores lógicos. Dou abaixo a fórmula mais concisa que acabou.

Para alguma sequência de números $$$(x_ {m}) = {x_ {1}, x_ {2}, x_ {3}, ... x_ {max}}$ nós introduzimos o operador de detecção do primeiro número igual a:

$$

$$\ mathbf {Dt_ {a}} (x_ {m}): = \ left \ {\ begin {matrix} m \ \ mathbf {se} \ \ existe \ m: \ forall \, k <m \ x_ {k } \ neq a \ \ mathbf {e} \ x_ {m} = a \\ 0 \ \ mathbf {caso contrário} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ end {matrix} \ right.$$

Todos os números primos, começando com 5, podem ser calculados pela fórmula:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1} + 2i) \, mod \, P_ {j + 1})), \ \ \ \ forall \, n \ geqslant 3 \\ \ forall \, i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ alpha -1}} {2} +10 \ ,, \ \ 2 \ leqslant \ alpha \ leqslant n-1; \ \ j_ {max} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1$$

Operador $$$\ mathbf {Dt_ {0} ^ {j}}$ itera $$$j$ o restante da divisão de cada número candidato por simplicidade com $$$i$ numero $$$(P_ {n-1} + 2i)$ para números primos já encontrados na faixa de até $$$P_ {j_ {max} +1}$ . Os números dos candidatos são selecionados em ordem no conjunto de números ímpares maior que o número primo anterior $$$P_ {n-1}$ . $$$\ pi (\ sqrt {P_ {n-1} + 2i})$ É uma função pi mostrando o número de primos $$$\ leqslant \ sqrt {P_ {n-1} + 2i}$ .
Operador $$$\ mathbf {Dt_ {0} ^ {i}}$ itera $$$i$ valores de saída do operador $$$\ mathbf {Dt_ {0} ^ {j}}$ até encontrar 0. Como a série de primos é infinita, isso acontecerá mais cedo ou mais tarde. Na saída do operador $$$\ mathbf {Dt_ {0} ^ {i}}$ sempre haverá algum número $$$i$ . Limite inferior $$$i_ {max}$ é determinado pela diferença máxima de números primos adjacentes menores que o desejado. O aumento nessa diferença ocorre logaritmicamente. O gráfico abaixo mostra a dependência do crescimento máximo e médio $$$\ Delta P _ {\ alpha}$ de n para os primeiros 100.000 números primos. O valor máximo foi amostrado e calculado a média para cada mil números.
O aumento máximo na diferença de números primos $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ para o valor máximo anterior $$$max (\ Delta P _ {\ alpha})$ igual a 20 (para a diferença de números primos 31397-31469 = 72 em relação à diferença 25523-25471 = 52). É na região onde a derivada do logaritmo do envelope $$$\ Delta P _ {\ alpha}$ ainda é grande o suficiente, e os números primos não são mais muito pequenos. Com base nesse valor, a condição para $$$i_ {max}$ . Graph $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ para os primeiros 50.000 números primos abaixo. Os valores foram calculados para cada mil.
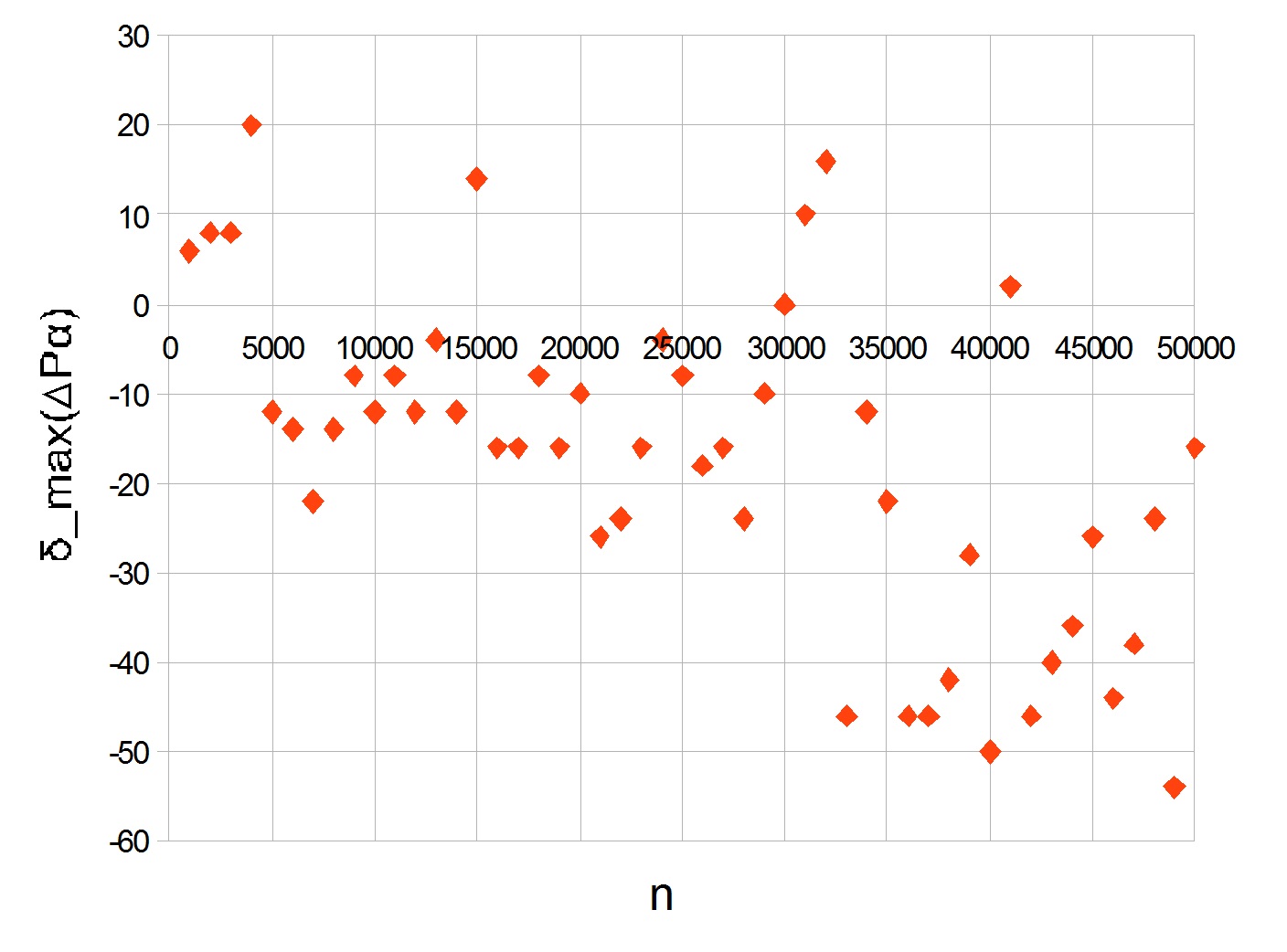
O pico é visível em 20. Com o aumento de n, o gráfico vai para menos, mostrando uma diminuição na taxa de crescimento de números primos grandes.

A segunda consideração é otimizar o cálculo de uma sequência de números primos.
O algoritmo estabelecido na fórmula acima é um método aprimorado para enumerar divisores. As melhorias são para excluir números pares da consideração e verificar a divisibilidade de apenas números primos menores que sq. as raízes dos números candidatos. A parte mais difícil do algoritmo é o cálculo do conjunto de funções mod restantes. A complexidade pode ser reduzida otimizando esta função. No entanto, existe uma maneira ainda mais eficaz. Vamos $$$(r_ {j + 1} ^ {n-1}) = {r_ {2}, r_ {3}, ... r _ {\ pi (\ sqrt {P_ {n-1}})}}$ É uma sequência de resíduos que divide o último número primo encontrado em números primos de 3 à raiz do mesmo. Faremos sequências do formulário

$$

$$(r_ {i, j + 1} ^ {n}) = {(r_ {2} + 2i) \, mod \, P_2, (r_ {3} + 2i) \, mod \, P_3, ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1}})}, (P_ {n -1} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1} + 2i})}} $$$

em ordem a partir de $$$i = 1$ . O último termo é calculado se $$$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ . Quando, em alguma etapa do cálculo, o restante $$$r_ {i, j + 1} ^ {n}$ se tornar igual a 0, vá para a próxima sequência. Isso é feito até que eu seja encontrado, no qual todos os resíduos são diferentes de zero. Isso significa encontrar o próximo número primo. Sequência $$$(r_ {j + 1} ^ {n})$ deve ser salvo até o próximo prime A fórmula recorrente para calcular números primos dessa maneira é convertida em:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} (r_ {i, j + 1} ^ { n})), \ \ \ \ forall \, n \ geqslant 3$$

No algoritmo apresentado, o mod de operação é facilitado: divisível por $$$(r_ {j + 1} + 2i) / P_ {j + 1}$ vezes mais divisores. As únicas exceções são a ocorrência de novos divisores simples. Na memória do computador, ao implementar o algoritmo, é necessário armazenar uma matriz de números primos na raiz do buscado, bem como uma matriz variável de resíduos. A complexidade do algoritmo no sentido geral (a quantidade de trabalho) pode ser menor que a de outros métodos conhecidos. As operações mais complexas são a extração da raiz quadrada, o cálculo de resíduos e a multiplicação. A raiz pode ser extraída para o número inteiro mais próximo. Para obter resíduos, você pode usar um algoritmo eficaz com base na regra geral de divisibilidade. A multiplicação é usada apenas por 2 números relativamente pequenos i . A complexidade do tempo do algoritmo pode ser reduzida distribuindo o trabalho de acordo com os valores de i . A peneira segmentada obtida dessa maneira deve funcionar mais rapidamente em computadores multithread. No entanto, o trabalho realizado será maior devido ao aumento de dividendos. Você também pode "parafusar" a fatoração da roda no algoritmo. Com o tamanho ideal das rodas, isso pode reduzir a complexidade em uma certa faixa de n - até que o hardware "acelere" a lentidão.

Talvez alguém venha a calhar meus pensamentos.