As árvores de pesquisa binária são uma estrutura de dados para armazenar itens com recursos de pesquisa rápida. A ideia é simples e engenhosa: "menos resta, mais está certo". É aí que termina a simplicidade e começam as complexas questões de equilibrar uma árvore para que ela não se transforme em um galho longo.

Neste artigo, forneceremos uma definição, listaremos as regras para colocar elementos em uma árvore vermelho-preta, consideraremos um algoritmo de balanceamento e consolidaremos o que foi dito em um exemplo. Estudamos esse tópico com mais detalhes, além de outros tipos de árvores de pesquisa binária no curso "Algoritmos para desenvolvedores" . A árvore vermelho-preta
A árvore vermelho-preta é uma árvore de pesquisa binária auto-balanceada, que garante um crescimento logarítmico da altura da árvore a partir do número de nós e a rápida execução das operações básicas da árvore de pesquisa: adição, exclusão e pesquisa de um nó.
A árvore vermelho-preta não está completamente equilibrada, em alguns lugares sua altura pode variar quase duas vezes. Essa suposição não afeta assintoticamente a velocidade de busca por elementos, mas acelera significativamente o posicionamento de novos elementos, porque você não precisa "agitar" a árvore toda vez que adicionar elementos, às vezes é suficiente adicionar um elemento vermelho sem tocar nos outros e sem alterar a "altura preta" .
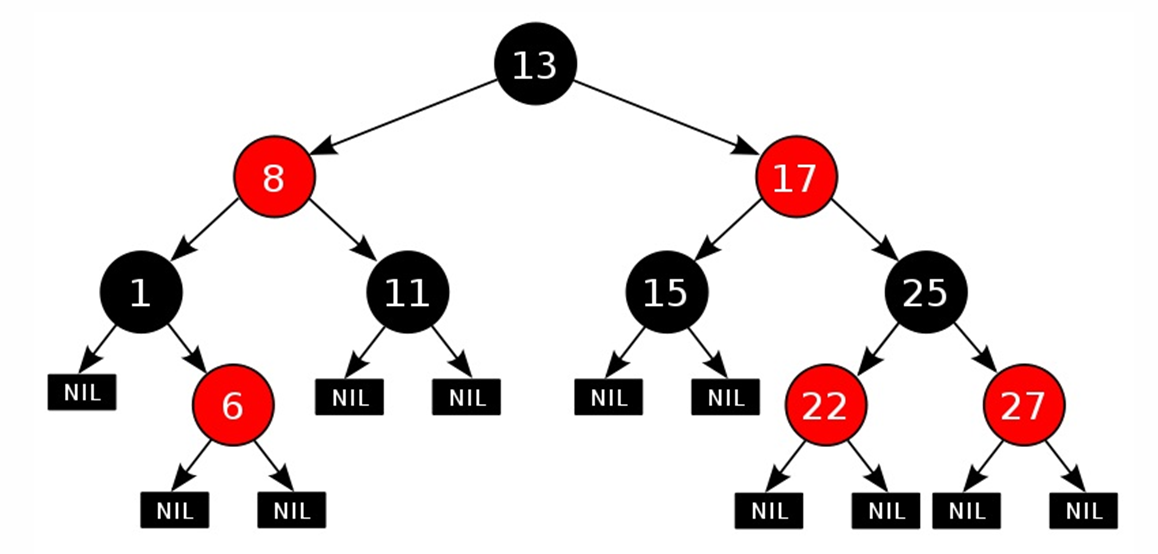
Regras para colocar elementos em uma árvore vermelho-preta
- Cada nó é vermelho ou preto; as folhas NIL são sempre pretas.
- A raiz da árvore é sempre preta
- Ambos os descendentes de cada nó vermelho são pretos
- O caminho de qualquer nó para qualquer folha descendente contém o mesmo número de nós pretos.
Quando você insere um novo elemento, ele recebe uma cor vermelha. Para cumprir as duas primeiras regras, basta redesenhar os novos vértices na cor desejada.
Considere as regras de balanceamento para a implementação de 3 e 4 pontos.
Em cada figura, supõe-se que já adicionamos um elemento X que viola a regra 3, precisamos alterar a estrutura da árvore para que a regra 3 seja executada e 4 não seja quebrado.
Legenda dos vértices:
- X - um elemento adicionado que viola 3 parágrafos das regras.
- P - item pai X
- G - o avô do elemento X, o pai do elemento P
- U é o tio do elemento X, o irmão do elemento P, o segundo filho do elemento G.
Caso Um - Tio Vermelho
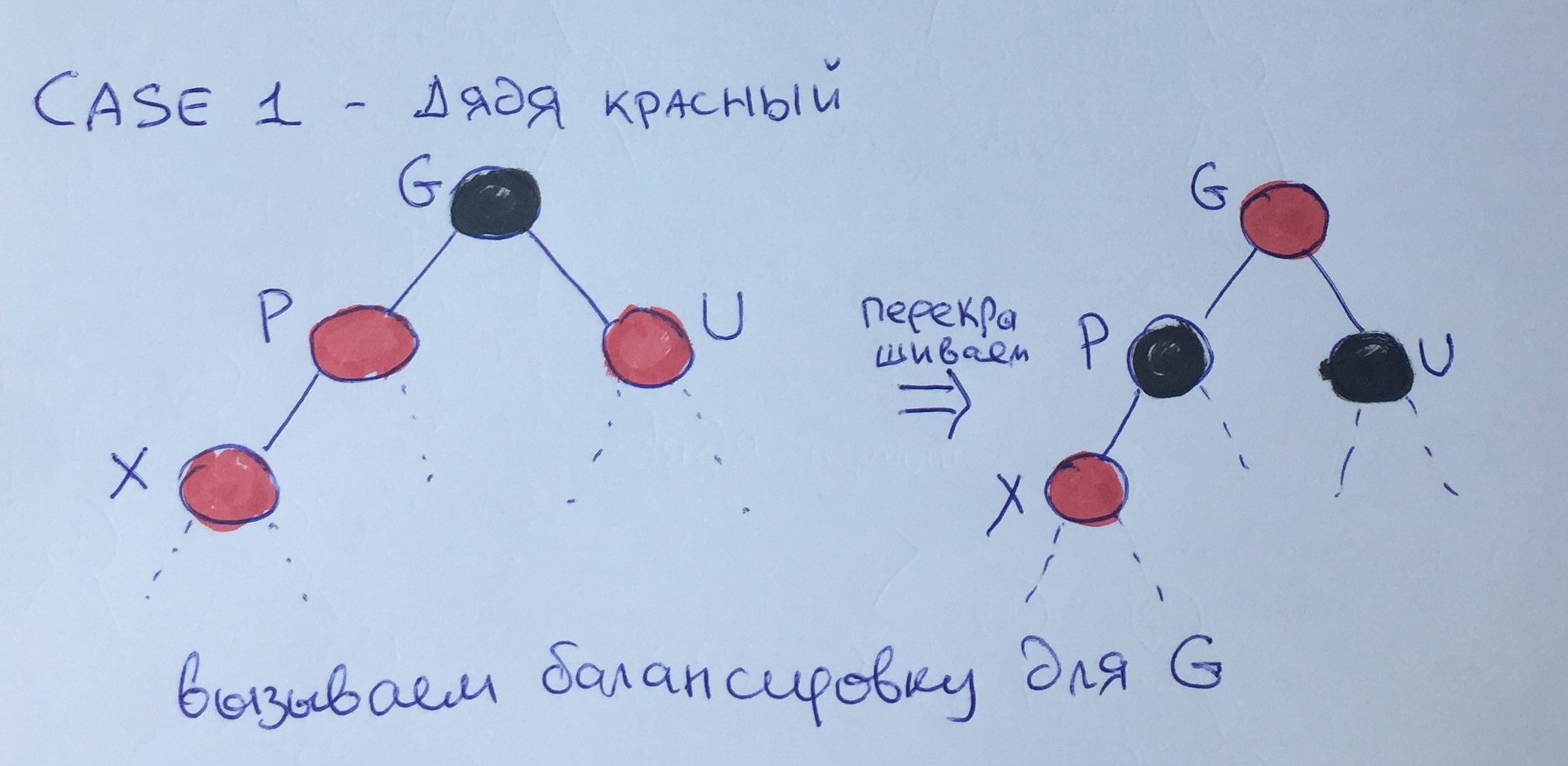
Se o pai e o tio são vermelhos, podemos "abaixar" a cor preta do nível do avô para o nível do pai e repintar os nós, como mostra a figura. Nesse caso, a "altura preta" permanecerá a mesma, no entanto, a violação da regra 3 para o elemento G é possível; portanto, é necessário chamar recursivamente o balanceamento adicional para esse nó.
Caso dois - um tio preto - pai e avô em direções diferentes.
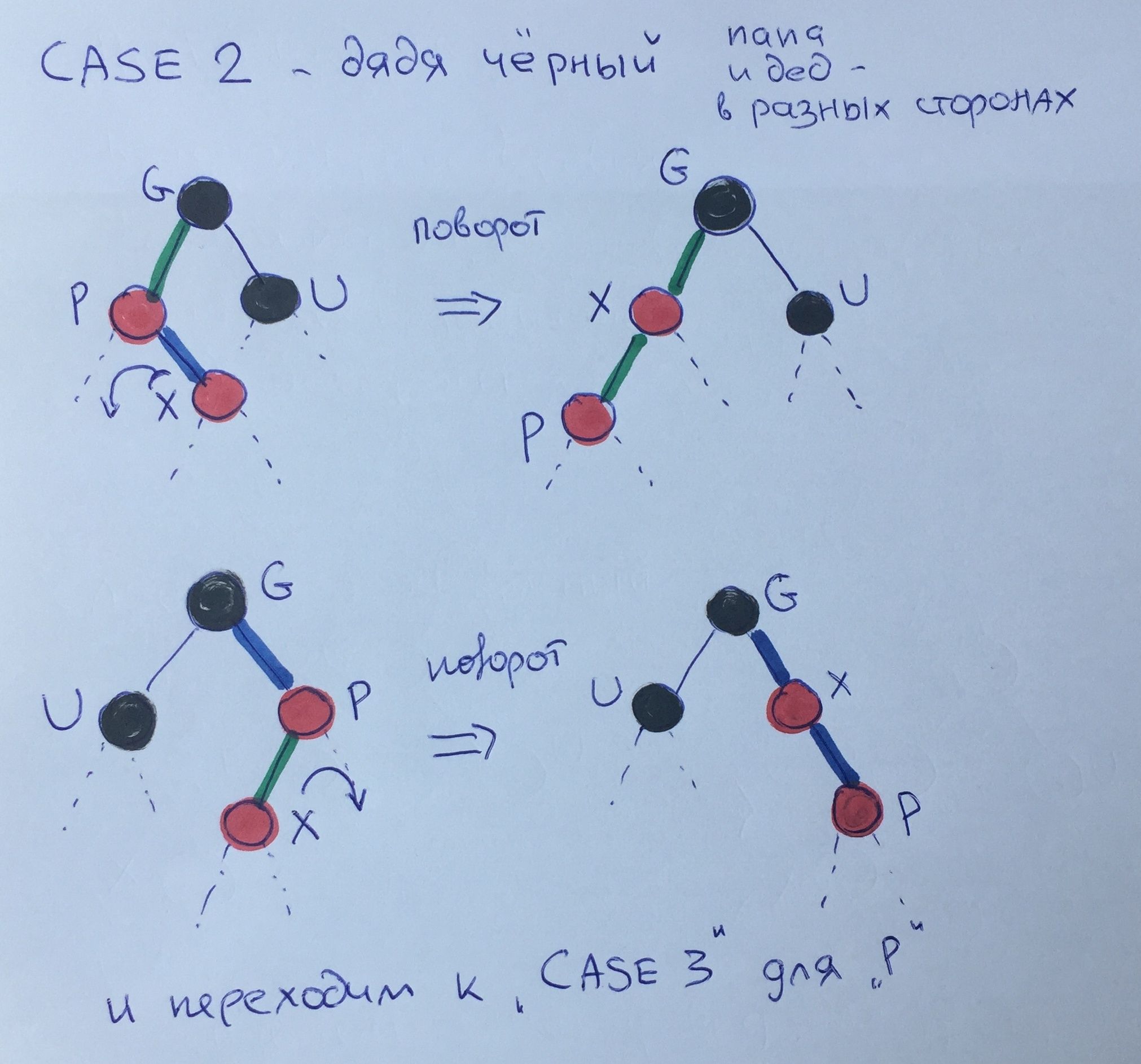
Essa estrutura deve ser levada ao terceiro caso, quando pai e avô vão na mesma direção. Para fazer isso, você precisa fazer uma pequena mudança do filho X para o pai (as regras de turnos não são consideradas neste artigo) e chamar 3 casos para o elemento R.
Caso Três - Tio Negro - Pai e Avô do Mesmo Lado
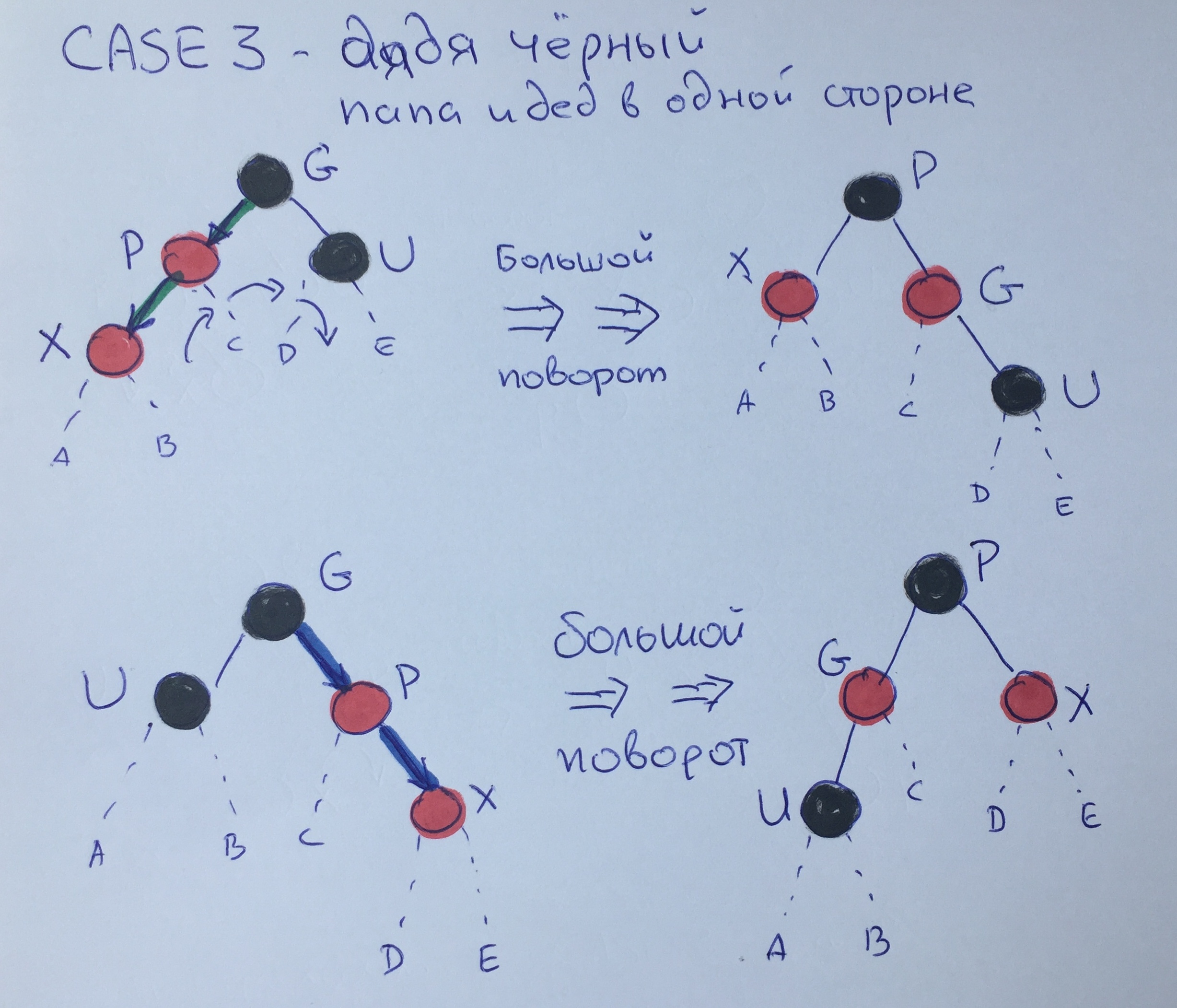
Nesse caso, já podemos mudar de pai para avô para tio preto e repintar P em preto e G em vermelho. Como resultado dessa rotação, a regra 3 será atendida.
Certifique-se de que a quarta regra também seja satisfeita. Suponha que antes da grande virada, a altura preta do elemento G fosse N + 2. A altura dos elementos "suspensos" será a seguinte:
A = N + 1,
B = N + 1,
C = N + 1
D = N
E = N.
Veja por si mesmo que depois de girar a regra 4 é verdadeira para todos os elementos.
Exemplo concreto
Agora, consideraremos o processo de formação de uma árvore vermelho-preta com inserção sequencial dos elementos 1, 2, 3, 4, 5 e 6.
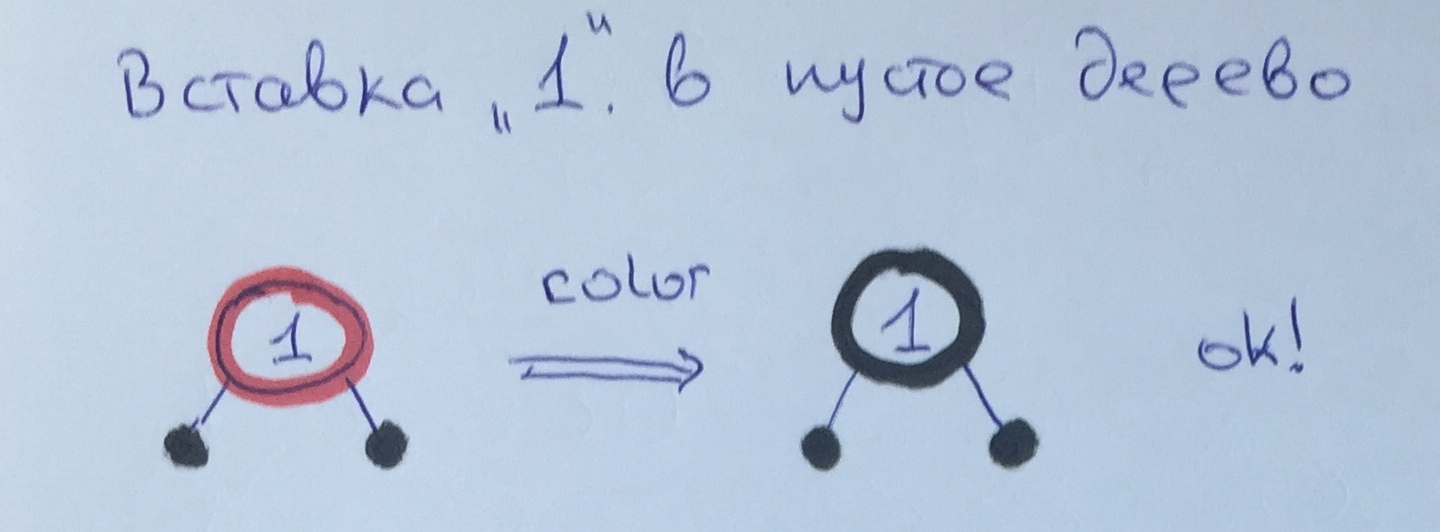
Como o elemento 1 é a raiz, simplesmente o repintamos para cumprir a regra 1.
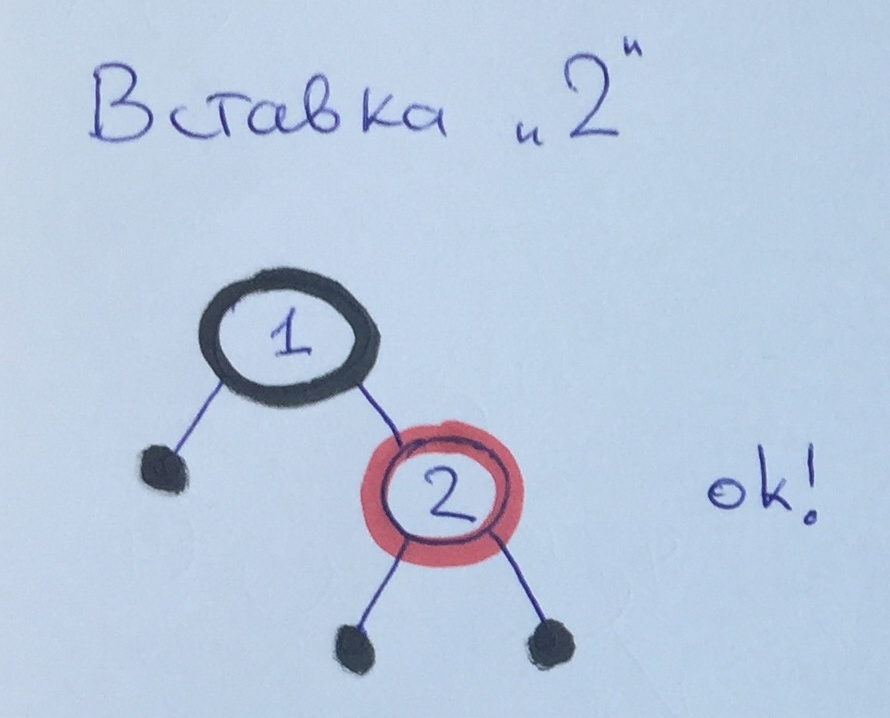
Após adicionar o elemento 2, todas as regras são executadas.
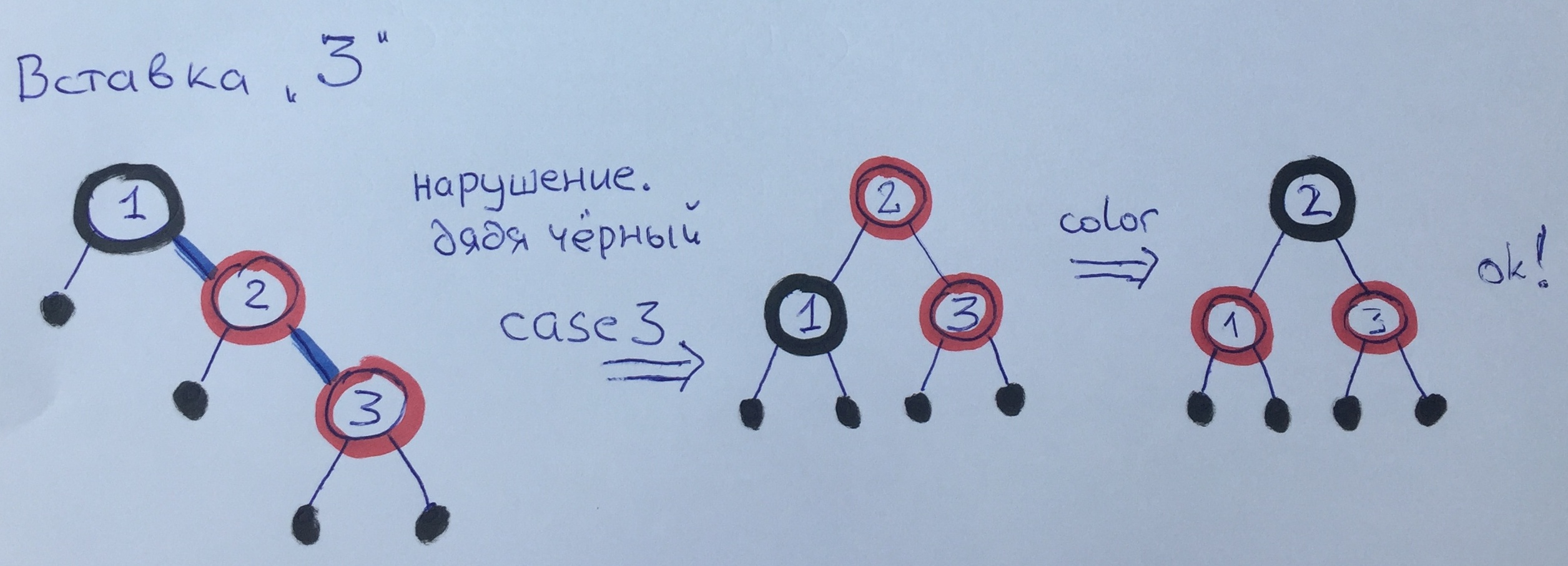
Ao adicionar o elemento 3, violamos a regra 3. Como temos um tio preto, avô e pai, por um lado, usamos o terceiro caso - fazemos uma curva e repintamos.
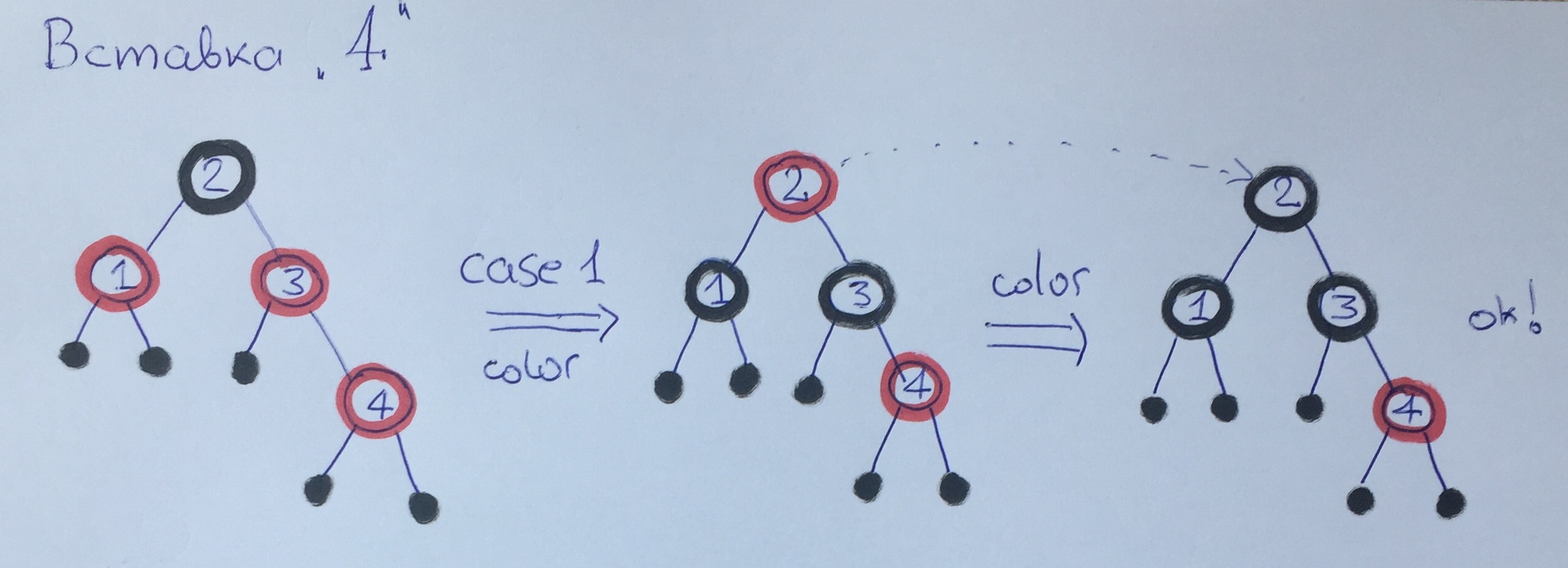
Ao adicionar o elemento 4, violamos novamente a regra 3. Desta vez, nosso tio está vermelho, então aplicamos o primeiro caso com repintura - a altura preta da árvore aumentará em 1. Observe. que o algoritmo de balanceamento é lançado adicionalmente para o avô - elemento 2, que, como a raiz, é simplesmente repintado em preto.
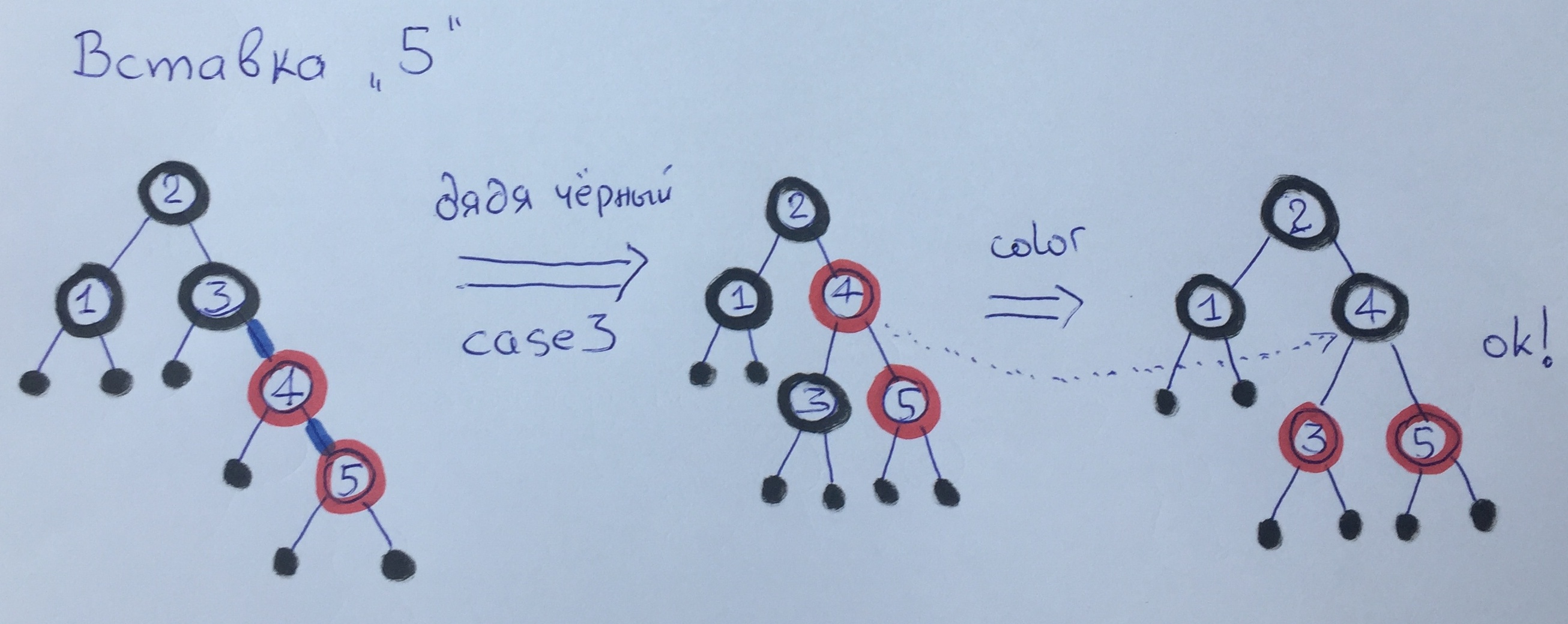
Ao inserir o elemento 5, aplicamos novamente o caso 3 - fazemos uma grande curva e repintamos os vértices. Observe que a altura do preto não mudou.
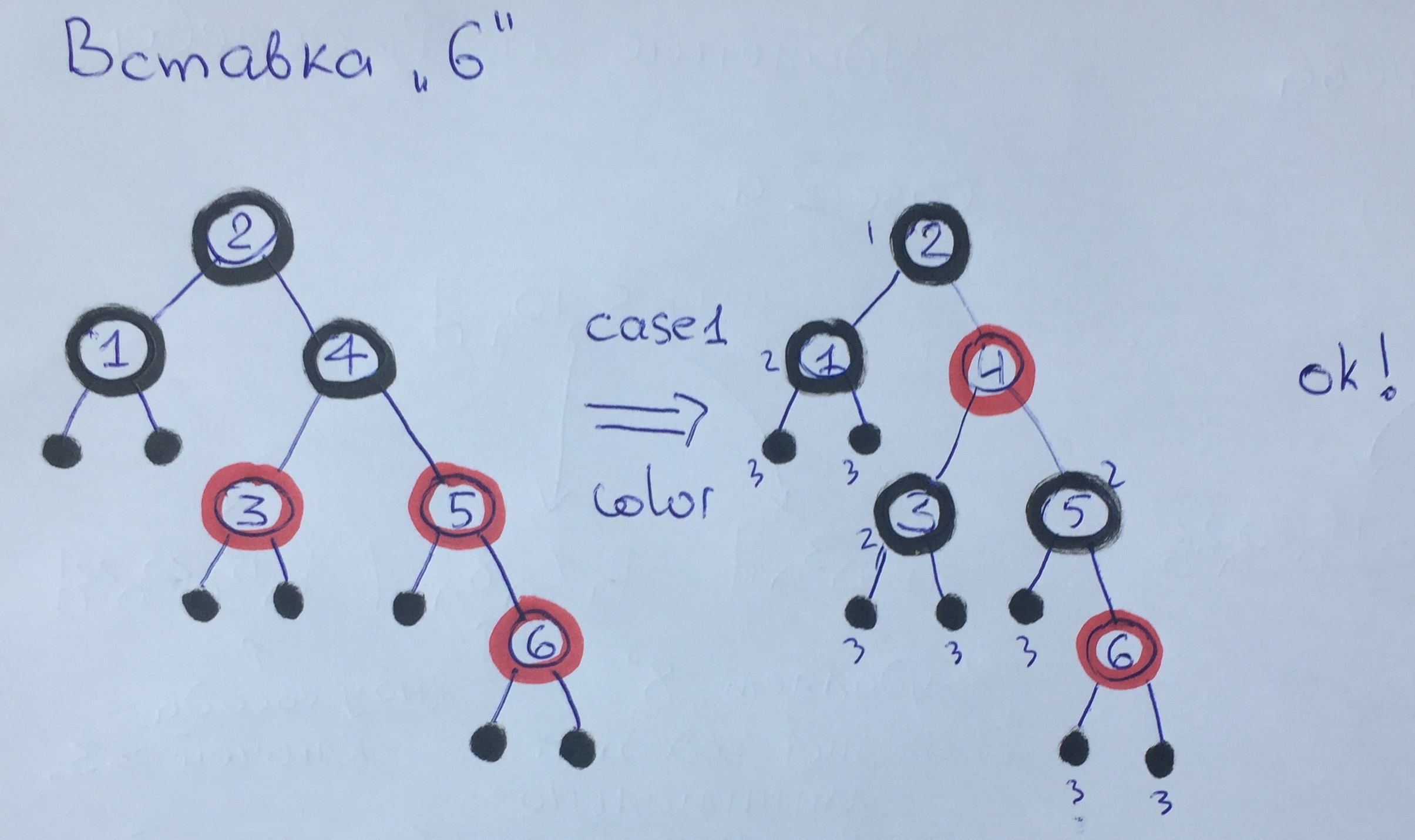
Ao adicionar o elemento 6, violamos novamente a regra 3. Como nosso tio é vermelho, aplicamos o primeiro caso com repintura, a altura do preto não mudou. A chamada de equilíbrio para 4 elementos não mudou nada na árvore, pois esse elemento não viola as regras.
Assim, nos familiarizamos com as questões de balanceamento de árvore vermelho-preta, com mais detalhes e com exemplos de algoritmos neste tópico, bem como com variedades de outras árvores de pesquisa binária, consideradas no curso
"Algoritmos para desenvolvedores" .