Descida de gradiente estocástico (SGD) para a função de perda logarítmica (LogLoss) em um problema de classificação binária

A parte anterior (sobre regressão linear, descida em gradiente e como tudo funciona) - habr.com/en/post/471458

Neste artigo, mostrarei a solução para o problema de classificação primeiro, como se costuma dizer, "canetas", sem bibliotecas de terceiros para SGD, LogLoss e gradientes de cálculo e, em seguida, usando a biblioteca PyTorch.

Objetivo: para duas características categóricas que descrevem o amarelo e a simetria, determine a qual classe (maçã ou pera) o objeto pertence (ensine o modelo a classificar objetos).

Para começar, faça o upload do nosso conjunto de dados:

import pandas as pd data = pd.read_csv("https://raw.githubusercontent.com/DLSchool/dlschool_old/master/materials/homeworks/hw04/data/apples_pears.csv") data.head(10) 

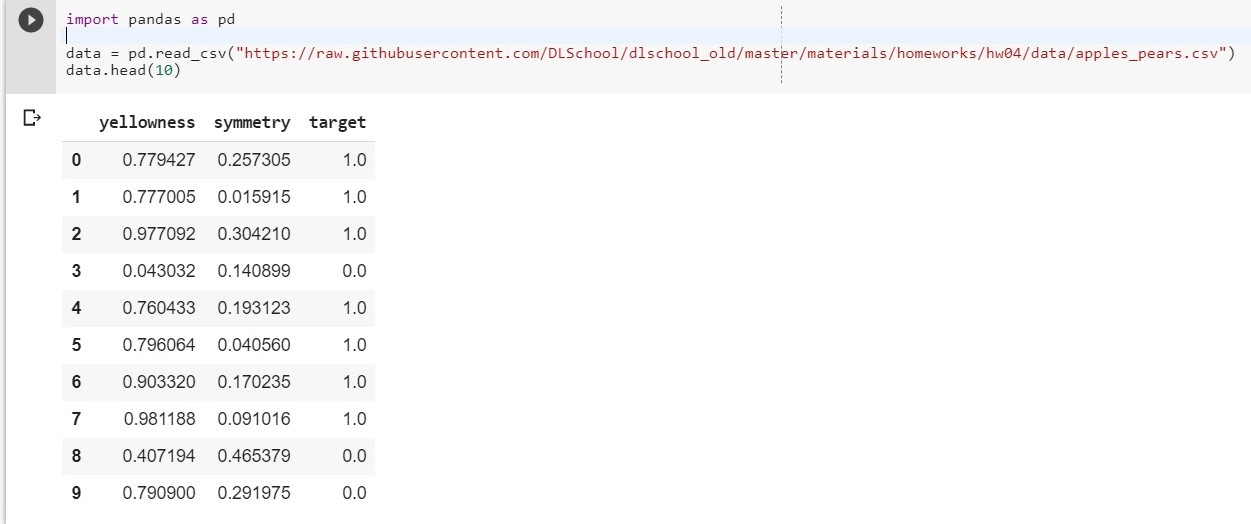
Let: x1 - amarelo, x2 - simetria, y = targer

Nós compomos a função y = w1 * x1 + w2 * x2 + w0
(w0 será considerado o viés (por. - viés))

Agora, nossa tarefa é reduzida para encontrar os pesos w1, w2 e w0, que descrevem com mais precisão a dependência de y em x1 e x2.

Usamos a função de perda logarítmica:



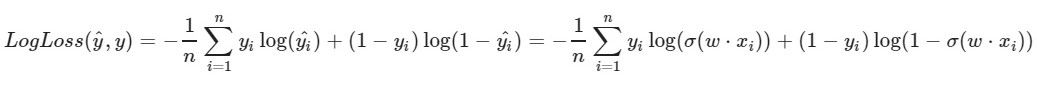
O parâmetro esquerdo da função é a previsão com os pesos atuais w1, w2, w0

O parâmetro correto da função é o valor correto (a classe é 0 ou 1)

σ (x) é a função de ativação sigmóide de x

log (x) - o logaritmo natural de x

É claro que quanto menor o valor da função de perda, melhor escolhemos os pesos w1, w2, w0. Para fazer isso, escolha uma descida de gradiente estocástico .

Observo que a fórmula do LogLoss terá uma visão diferente, pois no SGD selecionamos um elemento e não uma seleção inteira (ou uma subamostra, como no caso da descida do gradiente de minilote):


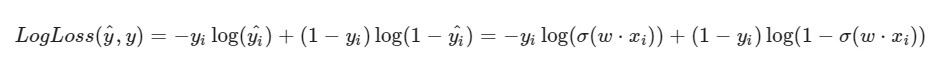Progresso da solução:

Os pesos iniciais w1, w2, w0 recebem valores aleatórios

Pegamos um certo i-ésimo objeto de nosso conjunto de dados (por exemplo, aleatório), calculamos o LogLoss para ele (com nossos w1, w2 e w0, aos quais atribuímos inicialmente valores aleatórios) e calculamos as derivadas parciais para cada um dos pesos w1, w2 e w0, atualize cada um dos pesos.

Um pouco de preparação:

 import pandas as pd import numpy as np X = data.iloc[:,:2].values #  - y = data['target'].values.reshape((-1, 1)) #  (    ) x1 = X[:, 0] x2 = X[:, 1] def sigmoid(x): return 1 / (1 + np.exp(-x)) 

Implementação:

 import random np.random.seed(62) w1 = np.random.randn(1) w2 = np.random.randn(1) w0 = np.random.randn(1) print(w1, w2, w0) # form range 0..999 idx = np.arange(1000) # random shuffling np.random.shuffle(idx) x1, x2, y = x1[idx], x2[idx], y[idx] # learning rate lr = 0.001 # number of epochs n_epochs = 10000 for epoch in range(n_epochs): i = random.randint(0, 999) yhat = w1 * x1[i] + w2 * x2[i] + w0 w1_grad = -((y[i] - sigmoid(yhat)) * x1[i]) w2_grad = -((y[i] - sigmoid(yhat)) * x2[i]) w0_grad = -(y[i] - sigmoid(yhat)) w1 -= lr * w1_grad w2 -= lr * w2_grad w0 -= lr * w0_grad print(w1, w2, w0) 

[0,49671415] [-0,1382643] [0,64768854]
[0,87991625] [-1,14098372] [0,22355905]

* _grad é a derivada do peso correspondente. Escreverei a fórmula geral:



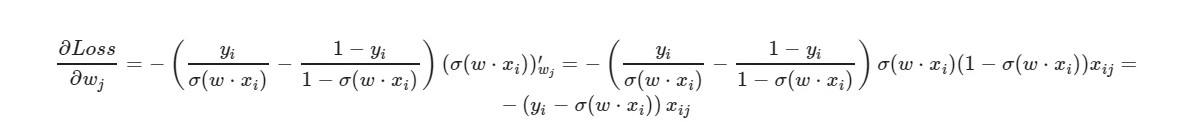
Para o termo livre w0 - o fator x é omitido (considerado igual a um).

Usando a fórmula final da derivada, podemos ver que não precisamos calcular explicitamente a função de perda (precisamos apenas derivadas parciais).

Vamos verificar quantos objetos do conjunto de treinamento nosso modelo fornece as respostas corretas e quantos - os errados.

 i = 0 correct = 0 incorrect = 0 for item in y: if(np.around(x1[i] * w1 + x2[i] * w2 + w0) == item): correct += 1 else: incorrect += 1 i = i + 1 print(correct, incorrect) 

925 75

np.around (x) - arredonda o valor de x. Para nós: se x> 0,5, então o valor é 1. Se x ≤ 0,5, então o valor é 0.

E o que faremos se o número de recursos do objeto for 5? 10? 100? E teremos a quantidade apropriada de pesos (mais um para viés). É claro que trabalhar manualmente com cada peso, calcular gradientes para isso é inconveniente.

Usaremos a popular biblioteca PyTorch.

PyTorch = NumPy + CUDA + Autograd (cálculo automático de gradientes)

Implementação do PyTorch:

 import torch import numpy as np from torch.nn import Linear, Sigmoid def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step X = torch.FloatTensor(data.iloc[:,:2].values) y = torch.FloatTensor(data['target'].values.reshape((-1, 1))) from torch import optim, nn neuron = torch.nn.Sequential( Linear(2, out_features=1), Sigmoid() ) print(neuron.state_dict()) lr = 0.1 n_epochs = 10000 loss_fn = nn.MSELoss(reduction="mean") optimizer = optim.SGD(neuron.parameters(), lr=lr) train_step = make_train_step(neuron, loss_fn, optimizer) for epoch in range(n_epochs): loss = train_step(X, y) print(neuron.state_dict()) print(loss) 

OrderedDict ([('0.weight', tensor ([[- 0.4148, -0.5838]])), ('0.bias', tensor ([0.5448]]]))
OrderedDict ([('0.weight', tensor ([[[5.4915, -8.2156]])), ('0.bias', tensor ([- 1.1130]]]))
0.03930133953690529

Perda bastante boa na amostra de teste.

Aqui, o MSELoss é selecionado como uma função de perda.

Mais sobre Linear

Em resumo: fornecemos 2 parâmetros para a entrada (nossos x1 e x2, como no exemplo anterior) e obtemos um parâmetro (y) para a saída, que, por sua vez, é alimentada na entrada da função de ativação. E então eles já estão calculados: o valor da função de erro, gradientes. No final - os pesos são atualizados.

Materiais utilizados no artigo