📸 👩🏼‍🏫 🎓 Tudo o que você queria saber sobre o pêndulo reverso 🐎 🏈 👨🏿‍🏭

O artigo serve como uma folha de dicas para quem quer fazer seu pêndulo reverso. Aqui estão os problemas pelos quais eu retrabalhei várias vezes, uma breve visão geral da teoria é necessária para entender como estabilizar o sistema.

Por que eu preciso disso?

Resumindo: eu queria expandir minha máquina CNC, mas algo deu errado ...

História completa

Desde a infância, eu queria ter minha própria máquina CNC, porque lidou com modelos de aeronaves nas quais você precisa fazer muitos pequenos detalhes repetidos. Primeiro comprei um kit de bricolage pronto e depois decidi aumentá-lo. Joguei por dois meses, mas ainda assim a máquina é pequena, a área de trabalho era de apenas 18 por 10 cm, não possui sensores de posicionamento. Decidi comprar um guia maior, colocar os interruptores de limite e instalar o carro no meio com um motor de passo. Fiz isso em meio dia, mas você não pode ir direto ao sonho - em um grande CNC, é necessário complicar a tarefa e colocar o pêndulo na carruagem, então me pareceu fácil, mas tive que me lembrar dos anos do instituto e me familiarizar com a TAU.

Tentativas malsucedidas

O projeto levou quase dois anos de tentativa e erro, redesenhando, aguardando detalhes e dias de folga incompletos para que aqueles que desejam repetir economizassem tempo e nervos, considero necessário conversar sobre decisões malsucedidas.

um giroscópio (MPU6050) em vez de um codificador - fundamentalmente nada contra ele, mas o sensor deve estar localizado em uma haste rotativa; isso introduz um efeito imprevisível e a incapacidade de rolar a haste várias vezes ao redor do eixo.
codificador absoluto - se for um potenciômetro, mesmo o movimento dos fios (principalmente devido a contatos no arduino) introduz ruído nas medições, um ADC de 10 bits ainda não é suficiente; se for um sensor mais caro, a leitura ocorre por meio de uma interface serial e isso introduz um atraso no sistema, especialmente em combinação com um motor de passo.
a rigidez do sistema - em algum momento, peguei um tubo de alumínio com carga no final, quando o carro vibrou, começaram a surgir fortes vibrações, e não ficou claro imediatamente qual sistema estávamos estabilizando. Devemos nos esforçar para garantir que o sistema físico esteja o mais próximo possível do que é modelado.
atrito - esse fenômeno geralmente é negligenciado, tentei reduzi-lo usando grandes rodas de carro e perfis de ranhura em V, em contraste com trilhos com barras deslizantes com pequenas bolas, porque o atrito de rolamento é inversamente proporcional ao raio.
o uso de um motor de passo - passei muito tempo tentando seguir esse caminho, é enganoso simplificar as fórmulas (na verdade, controlamos imediatamente a aceleração da base do pêndulo) e a simplicidade do design (podemos esquecer o atrito no trilho, o codificador do motor, se assumirmos que o motor não pula etapas) , mas ... Para controlar com precisão a velocidade, o tempo entre as etapas deve ser dezenas de microssegundos, o que significa que você pode esquecer a saída do estado no console. Sem feedback, você não pode ter certeza de que o motor não perdeu as etapas e a velocidade é realmente o que o sistema pensa. Não afirmo que essa seja uma solução sem saída; se alguém conseguir estabilizar o pêndulo com um motor de passo, ficarei feliz em analisá-lo.

Pêndulo livre

Para concluir a imagem, simulamos um pêndulo em uma carruagem livre sem atrito.

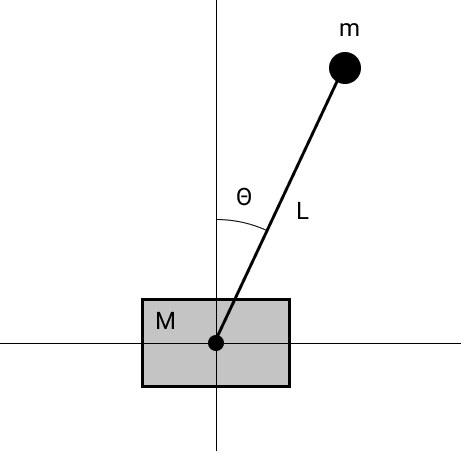
As equações de movimento podem ser obtidas pela diferenciação do Lagrangiano em relação às coordenadas generalizadas. Obtemos as seguintes equações:

b e g i n c a s e s L c d o t d d o t t h e t a + g c d o t s i n (t h e t a) - d d o t x c d o t c o s (t h) = 0 (m + M) c d o t d d o t x + m c d o t d d o t t h e t a c d o t L c d o t c o s (t h e t a) - m c d o t L p o n t o {t h e t a}^{2} c d o t s i n (t h e t a) = 0 e n d c a s e s

$\ begin {cases} L \ cdot \ ddot \ theta + g \ cdot {sin (\ theta)} - \ ddot {x} \ cdot {cos (th)} = 0 \\ (m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ ponto {\ theta} ^ 2 \ cdot {sin (\ theta )} = 0 \ end {cases}$

a partir do qual você pode encontrar como o vetor de estado muda:

b e g i n c a s e s d o t t h e t a = w d o t w = f r a c g c d o t s i n (t h e t a) + b c d o t L c d o t w^{2} c d o t s i n (t h e t a) c d o t c o s (t h e t a) L c d o t (1 + b c d o t c o s^{2} (t h e t a)) d o t x = v d o t v = b c d o t f r a c L c d o t w^{2} c d o t s i n (t h e t a) - g c d o t s i n (t h e t a) c d o t c o s (t h e t a) 1 + b c d o t c o s^{2} (t h e t a) e n d c a s e s, b = f r a c m M + m

$\ begin {cases} \ dot \ theta = w \\ \ dot {w} = \ frac {g \ cdot {sin (\ theta)} + b \ cdot {L} \ cdot {w ^ 2} \ cdot { sin (\ theta)} \ cdot {cos (\ theta)}} {L \ cdot (1 + b \ cdot {cos ^ 2 (\ theta))}} \\ \ dot {x} = v \\ \ dot {v} = b \ cdot \ frac {L \ cdot {w ^ 2} \ cdot {sin (\ theta)} - g \ cdot {sin (\ theta)} \ cdot {cos (\ theta)}} {1 + b \ cdot {cos ^ 2 (\ theta)}} \ end {cases}, b = \ frac {m} {M + m}$

e simule o sistema. O código está aqui .

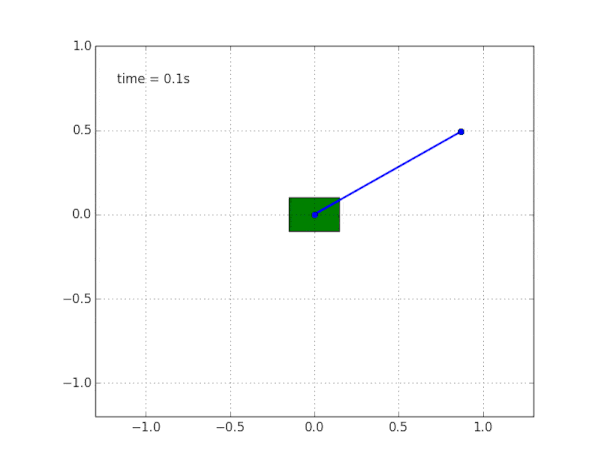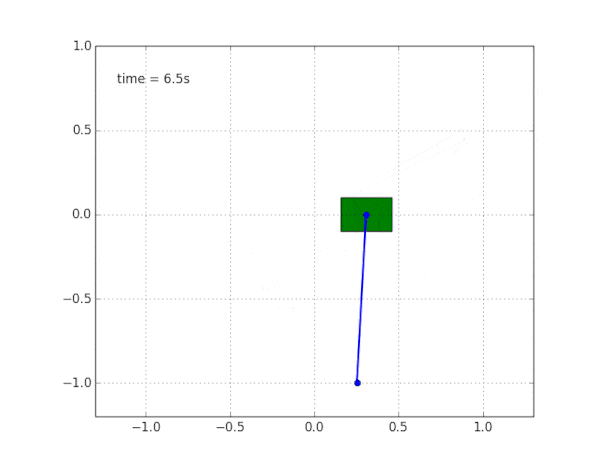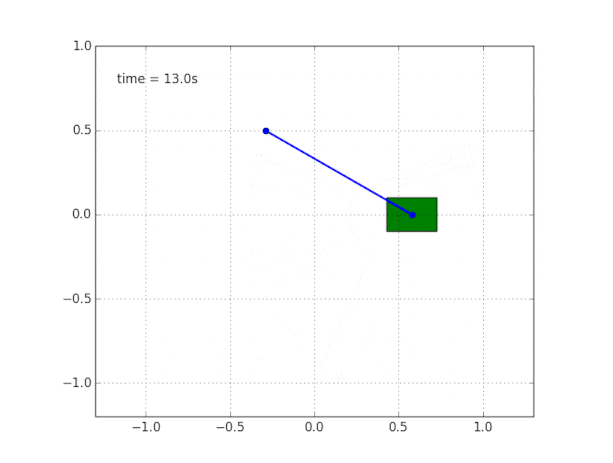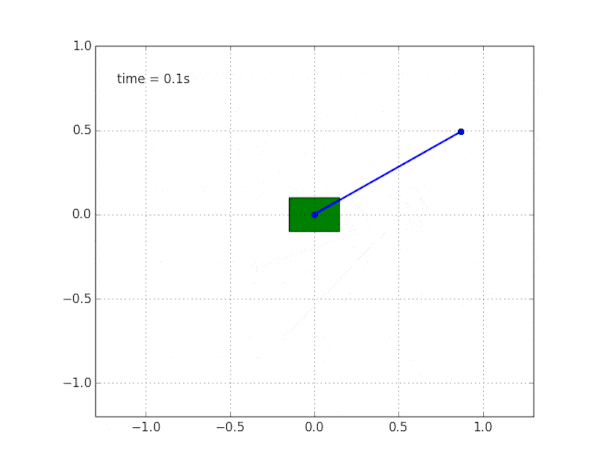
Por que o sistema é instável?

O bom senso e a visualização nos dizem que o próprio pêndulo não se sustenta. Mas como verificar isso matematicamente?
Em termos gerais, o sistema e a solução linearizados são os seguintes:

p o n t o m a t h b f x = A m a t h b f x, m a t h b f x (t) = e^{A t} m a t h b f x (0)

$\ ponto {\ mathbf {x}} = A \ mathbf {x}, \ mathbf {x} (t) = e ^ {At} \ mathbf {x} (0)$

Um expoente no poder da matriz parece mais claro, se formos para o sistema de coordenadas a partir de vetores próprios, então a matriz

A

$A$ será diagonal (

D

$D$ ) e o expositor terá a seguinte aparência:

e ^ {Dt} = \ begin {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}

$e ^ {Dt} = \ begin {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}$

Agora é visto, na presença de autovalores (

l a m b d a_{i}

$\ lambda_i$ ) com uma parte real positiva, o componente correspondente do vetor de estado tenderá ao infinito e o sistema desmoronará. O exposto acima se aplica a sistemas contínuos. Mais informações sobre sustentabilidade são descritas nesta vídeo aula.
Verifique se esse é o caso do pêndulo reverso. Linearizamos nosso sistema perto da posição de equilíbrio para

t h e t a = 0, s e n (t h e t a) a p p r o x t h e t a, c o s (t h e t a) a p p r o x 1, w^{2} a p p r o x 0

$\ theta = 0, sen (\ theta) \ approx \ theta, cos (\ theta) \ approx 1, w ^ 2 \ approx 0$ :

\ begin {bmatrix} \ ponto \ theta \\ \ ponto \ omega \\ \ ponto {x} \\ \ ponto {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}

$\ begin {bmatrix} \ ponto \ theta \\ \ ponto \ omega \\ \ ponto {x} \\ \ ponto {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}$

Autovalores diferentes de zero têm a forma

p m s q r t f r a c g L (1 + b)

$\ pm \ sqrt {\ frac {g} {L (1 + b)}}$ , assim nos convencemos da instabilidade.

Adicionar feedback

Agora a força atuará no carro

f

$f$ , uma das equações pode ser reescrita no formato:

(m + M) c d o t d d o t x + m c d o t d d o t t h e t a c d o t L c d o t c o s (t h e t a) - m c d o t L p o n t o {t h e t a}^{2} c d o t s i n (t h e t a) = f

$(m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ ponto {\ theta} ^ 2 \ cdot {sin (\ theta)} = f$ , e o sistema linearizado assumirá a forma:

\ begin {bmatrix} \ ponto \ theta \\ \ ponto \ omega \\ \ ponto {x} \\ \ ponto {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix} + \ begin {bmatrix} 0 \\ \ frac {1} {L} \ frac {1} {2m + M} \\ 0 \\ \ frac {1} {2m + M} \ end {bmatrix} \ cdot {f}

Agora o sistema (

d o t m a t h b f x = A m a t h b f x + B u

$\ dot {\ mathbf {x}} = A \ mathbf {x} + Bu$ ) tornou-se controlável , isso pode ser verificado verificando se a classificação da matriz

\ begin {bmatrix} B && AB && A ^ 2B && A ^ 3B \ end {bmatrix}

$\ begin {bmatrix} B && AB && A ^ 2B && A ^ 3B \ end {bmatrix}$ igual à dimensão do vetor de estado, ou seja, 4. Para manter o pêndulo na posição vertical, usei um controlador de estado linear-quadrático, ou seja controle (u ou f) é o produto do vetor de estado

[t e t a, p o n t o t e t a, x, p o n t o x]

$[\ teta, \ ponto {\ teta}, x, \ ponto {x}]$ por um vetor de parâmetros que são encontrados uma vez, minimizando o funcional quadrático . O código de simulação está aqui .

Controle do motor

Agora você precisa controlar o motor DC, ele contém muitos parâmetros que eu não conheço, então usei uma "caixa preta", descrita pelas seguintes equações, levando em consideração o atrito:

b e g i n c a s e s d o t x = v d o t v = - a c d o t v + b c d o t U + c c d o t s i n a l (v) e n d c a s e s

$\ begin {cases} \ dot {x} = v \\ \ dot {v} = -a \ cdot {v} + b \ cdot {U} + c \ cdot {sinal (v)} \ end {cases}$

Você pode ler sobre a derivação de equações e estimativa de parâmetros aqui . Abaixo, dou meus gráficos da aceleração do motor com o carro, dependendo da tensão (na realidade, o sinal PWM é emitido pelo controlador) e as curvas ajustadas.

Eu também encontrei os coeficientes do modelo por força bruta, o código .
Assim, o controlador nos fornece a aceleração necessária e, a partir da 2ª equação, conhecendo todas as constantes, encontramos a tensão.

Juntando o dispositivo real

Agora temos todo o conhecimento para coletar e estabilizar o pêndulo. Eu usei o seguinte ferro:

O Arduino Mega 2560 não é UNO, porque dois codificadores precisam de 4 pinos para interrupções
O codificador para o pêndulo - OMRON E6B2-CWZ6C 2500 pulsos por rotação - fornece o ângulo, calculamos a velocidade angular, a resolução é bastante alta, portanto houve diferenças finitas suficientes sem suavização e cálculo de médias
Codificador para o motor - LPD3806-600BM-G5-24C 600 pulsos por rotação - fornece a posição do carro, calcula a velocidade
Motor de 12V DC com caixa de engrenagens 5: 1
10Amp 5V-30V Motor Driver

Assim, medimos explicitamente o ângulo do pêndulo, a posição do carro, calculamos a velocidade angular do pêndulo e a velocidade do carro - obtemos o estado completo, encontrei os parâmetros do controlador com este script. Surpreendentemente, tudo rapidamente funcionou como estava. Estou satisfeito com o resultado, fica de pé e até segura um copo!

O código para o Arduino está aqui
O que poderia ser melhorado em comparação com muitas das opções que podem ser encontradas no youtube - este pêndulo é silencioso porque o PWM é ajustado fora da faixa auditiva e são usadas rodas de plástico.
Agora, esta tarefa parece um trabalho de laboratório: medir os parâmetros do motor e encontrar os coeficientes do regulador, entendendo simultaneamente o que está acontecendo.

O que vem a seguir?

Eu pretendo produzir um pêndulo: fazer um balanço, livrar-se de uma bobina de fios, fazer um escudo com conectores convenientes, para que não seja uma pena doar para alguma escola ou museu. Se alguém quiser participar, ficarei feliz em ter muitas idéias mais ambiciosas.

Referências

Descrição detalhada do problema do pêndulo inverso
Mastigamos um regulador linear-quadrático para controlar um pêndulo invertido - este artigo economizou muito tempo ao construir meu pêndulo
Excelentes palestras em vídeo TAU

Obrigado pela atenção!

Tudo o que você queria saber sobre o pêndulo reverso