Um breve guia de matemática para estrangeiros

Sobre o que é isso

E como se pode compor o material necessário dos primeiros cursos da universidade nos quarto dez e com aversão à álgebra?

Para a loucura dos bravos cantamos uma canção!

O público-alvo do Guia são aqueles que de repente se interessam por matemática ou sentem necessidade de aumentar sua eficácia profissional, mas, por algum motivo, não conseguem dedicar vários anos de sua vida a uma educação acadêmica. Se você precisa entender, mas falta muito conhecimento fundamental e se sente um estrangeiro em um país da matemática, onde eles falam uma língua incompreensível, tente seguir esse caminho como turista. A rota inteira é um passeio turístico e foi projetada por vários dias, no máximo duas semanas. Para comparação: um curso acadêmico completo é de cerca de cinco anos. O objetivo final da rota proposta é familiarizar-se com os princípios de uma seção altamente especializada - criptografia elíptica. No entanto, não é necessário ir até o fim se esta seção estiver fora do escopo de seus interesses ou se você se deparar com sérias dificuldades ou perigos. Porém, desde que você adquiriu o Guia, tente chegar ao menos no final da seção "Idioma da fórmula".

Como um dicionário, este guia também pode ser usado para tradução reversa. Talvez seja útil para matemáticos que são forçados a entrar em contato e trabalhar em estreita colaboração com não-matemáticos, constantemente superando a lacuna de mal-entendidos. Esse caso parece tão difícil que a linha de Maxim Gorky na epígrafe é uma resposta universal para ambos os lados. De qualquer forma, espero receber feedback e tentar reabastecer nosso conhecimento sobre por que eles não nos entendem e como isso pode ser corrigido.

E agora, sabendo que não há estradas reais aqui, tentaremos pavimentar pelo menos um caminho turístico.

Idioma da fórmula

Disseram-me que cada fórmula incluída no livro reduzirá pela metade o número de clientes. Então eu decidi ficar sem fórmulas. É verdade que, no final, eu ainda escrevi uma equação - a famosa equação de Einstein E = mc ^ 2. Espero que isso não afaste metade dos meus leitores em potencial.
Stephen Hawking - Uma Breve História do Tempo

Se o editor da Hawking estiver certo, adicionar apenas 33 fórmulas é suficiente para tornar o número de leitores em potencial próximo de zero. Vamos tentar?

Antes de tudo, é necessário alcançar um nível suficiente de entendimento da notação. Lembre-se, a matemática é uma linguagem.

Em uma primeira aproximação, várias camadas de entendimento de um texto matemático podem ser distinguidas. A primeira camada é a seleção de lexemas, a chamada análise lexical. O segundo é a construção de expressões e outras construções semânticas. Os programadores chamam isso de palavra análise, ou seja, análise e matemáticos gerais geralmente não o chamam, pois usam esse mecanismo subconscientemente. A seguir, estão as camadas responsáveis ​​pela compreensão da área de assunto, do significado físico e tudo mais.

Alguns matemáticos vêem os programadores como não matemáticos. Isso é injusto. Em primeiro lugar, os programadores precisam lidar com uma máquina que não perdoa as omissões no texto dos programas. Compare com um artigo científico típico, onde as expressões "óbvio", "fácil de mostrar", "não é óbvio" etc. são frequentemente usadas, mas, na realidade, as transições não são profundamente óbvias. Portanto, graças à programação, nasceu todo um ramo da matemática dedicado às linguagens formais e sua análise. Em segundo lugar, em condições adversas, as próprias linguagens de programação e as ferramentas relacionadas evoluíram. Veja como linguagens elegantemente modernas resolvem o problema de corresponder variáveis ​​a objetos. A propósito, um problema sério é não se confundir na notação quando há muitos deles, e eles vêm de fontes diferentes. E se você gastar um pouco de tempo em uma rápida visão geral de linguagens específicas como Coq, Agda, Idris, verá a conexão mais próxima entre a matemática e a própria programação.

Análise lexical

Eu costumava saber como as letras são escritas, eu acreditava no poder das palavras.
Crematório - Última Chance

Primeiro, pergunte a um amigo programador o que é um lexer e um analisador. Você não precisa se aprofundar, basta entender por exemplos o que é um token. Se você ouvir palavras estranhas como "el-er-parser" ou "syntax tree", saia silenciosamente da sala. Provavelmente, você já tem o suficiente, o programador não é mais necessário. Diger seus conhecimentos. Então você precisa aprender a distinguir tokens em textos matemáticos reais. Pratique em artigos baixados aleatoriamente. Evite documentos em formatos diferentes de pdf, bem como textos dispostos imediatamente em páginas da web. No entanto, existem sites sobre os quais é sabido que eles podem exibir corretamente textos matemáticos (Wikipedia e Habr estão incluídos na lista branca). Livros de papel também são geralmente adequados. Não tente extrair significado dos textos encontrados, apenas treine para analisar fórmulas.

Cartas

• As letras de dois alfabetos são geralmente usadas - latim e grego, mas as letras cirílicas e hebraicas são às vezes encontradas. Acontece que as letras de diferentes alfabetos coincidem em grande estilo. Na carta, isso não causa problemas, pois duas letras diferentes do mesmo tipo não são usadas no mesmo texto. No entanto, você pode encontrar a zombaria dos matemáticos se, por exemplo, você ler B em voz alta como "be" quando você quer dizer "beta". Esteja psicologicamente preparado para isso, você tem que suportar.
• Letras maiúsculas e minúsculas representam objetos diferentes. (Para alguns, isso parece óbvio demais, mas considero necessário pronunciá-lo explicitamente. Uma vez eu precisei apresentar a essência do meu trabalho aos meus colegas do departamento de patentes. Quando quase cheguei ao caráter da anedota “pai, onde está o mar?”, Percebi subitamente que as meninas consideram que minhas designações me referem ao mesmo objeto. Assim que o mal-entendido foi esclarecido, todo o processo, graças ao profissionalismo em seu trabalho, terminou rápida e decisivamente em completo sucesso.)
• A mesma letra, escrita em fontes diferentes, significa objetos diferentes.

Como regra (em álgebra), uma letra é um token independente. Se várias letras forem escritas em uma linha, a multiplicação será implícita. Por exemplo, abc significa o produto de a, bec. No entanto, existem exceções. Primeiro de tudo, este é o nome de muitas funções padrão e outras notações, que é um token de várias letras: $$$\ sin, \ cos, \ min, \ max, \ sup, \ lim$ etc. Eles geralmente são representados no estilo reto (romano), ao contrário de outros tokens de letras escritos em itálico. Além disso, na ciência da computação e em algumas outras áreas, eles se afastam dessa regra, onde uma sequência de letras indica um único símbolo de palavra. Se, em um caso específico, houver a menor dúvida, consulte um especialista.

Suportes

O papel mais importante em termos de análise é desempenhado por parênteses. Você provavelmente já sabe ou acha que parênteses são usados ​​para agrupar tokens. Mas há exceções. Se a fórmula lhe parecer estranha e contiver pares extras de colchetes, ou mesmo o equilíbrio dos colchetes estiver quebrado, provavelmente você encontrará um exemplo com um uso alternativo de colchetes. Vá a um especialista para obter esclarecimentos.

Índices

Preste atenção aos índices superior e inferior. É assim que a tipografia se parece com sobrescrito e subscrito. O sobrescrito é mais simples: como regra, significa exponenciação. Com o fundo um pouco mais difícil. Pode ser entendido de duas maneiras:

• Como uma operação de mapeamento. Por exemplo $$$x_i$ É uma função $$$x$ que toma como argumento $$$i$ . Se agora esse ponto não estiver claro, tudo bem, este lugar pode ser ignorado por enquanto.
• Como forma de formar um novo token quando as letras convenientes já terminarem. Pode-se freqüentemente assumir que $$$a_1, a_2, a_i$ - estes são apenas três objetos diferentes.

Em algum momento, pode parecer que esses dois pontos são essencialmente a mesma coisa. Não se preocupe, isso é normal, você se tornou um pouco mais próximo da iluminação. Agende uma reunião com um especialista.

Outros personagens

Os matemáticos são estetas. Eles amam quando não apenas o conteúdo, mas também a forma é linda. Eles ficam satisfeitos quando as fórmulas são digitadas em uma tipografia boa e adequada. Knut fez um delicioso pão de gengibre chamado $$$\ TeX$ . Faça um tutorial sobre como digitar e digitar fórmulas e encontre as tabelas de símbolos lá. Agora é importante para você como esses símbolos são classificados: letras, operadores, sinais de relacionamento, setas ... Sem se aprofundar no significado matemático dos símbolos, tente entender como os símbolos de cada classe são usados ​​sintaticamente. Por exemplo, há uma classe de operações binárias para a qual equidistantes direito e esquerdo do símbolo de operação devem ser algum tipo de subexpressão.

Figuras

Os não matemáticos acreditam que os matemáticos acreditam. De fato, os matemáticos raramente são considerados e os números são usados ​​principalmente para numerar objetos. Aparentemente, portanto, a seção "Números" foi adicionada às pressas e segue ilogicamente a seção "Outros símbolos". Você mesmo pode contar aos especialistas como os tokens digitais são formados e o que eles significam.

Convenções de notação

Sejam a, b, c, d, e, f números reais, onde e não é necessariamente igual à base dos logaritmos naturais, embora possa coincidir com ele.

Em matemática, existem convenções sobre quais caracteres usar em quais casos. No entanto, em diferentes seções, esses acordos podem variar. É como dialetos de um idioma. Existem notações padronizadas em toda a matemática. Confira as convenções aceitas na sua área de assunto. Além disso, alguns estudiosos são negligentes e às vezes violam acordos geralmente aceitos. Infelizmente, na maioria dos casos, não existem conjuntos de regras sobre esse assunto. Você pode discutir isso com o seu especialista ocasionalmente.

Embora a matemática seja geralmente supranacional, existem diferenças culturais. Você pode encontrá-los se desviar muito da rota sugerida pelo Guia. Por exemplo, as designações em inglês e russo de funções tangentes, cotangentes e hiperbólicas são distinguidas. Além disso, as mesmas letras podem ser pronunciadas de maneira diferente, dependendo das tradições culturais. Para economizar esforço, aprenda os nomes em inglês de todas as letras, incluindo grego. Se você não pulou a escola, pelo menos não haverá problemas com o alfabeto latino. Se você usá-los em russo, seus interlocutores podem franzir a testa, mas desta vez eles terão que aguentar. Se você quiser fazê-los felizes, aprenda os nomes das letras latinas e gregas aceitas na cultura matemática de língua russa.

Análise

Expressões

Você provavelmente já ouviu o termo "árvore" não no botânico, mas no sentido matemático. Isso é algo bastante simples, se necessário, atualize seu conhecimento. Portanto, uma expressão matemática tem uma estrutura em árvore. Isso significa que a expressão consiste em subexpressões que consistem em subexpressões ... Mas esse processo não é infinito, mas termina com algumas subexpressões que consistem em tokens.

Alguns tokens são expressões elementares. Por exemplo, números (mais precisamente, literais numéricos) e variáveis. E alguns exigem que argumentos sejam adicionados a eles em certas posições, ou seja, algum tipo de subexpressão. Então eles formam uma expressão maior. Por exemplo, o símbolo de uma operação de adição requer expressões à direita e à esquerda dela. Podemos dizer que o lexeme tem alguma aridade ou, se você preferir química, valência, é quantas e em que lugares você precisa adicionar ao lexeme das subexpressões para formar uma expressão. Para operação, + arity pode ser descrito da seguinte maneira: $$$\ cdot + \ cdot$

Essa entrada significa exatamente que o token + requer argumentos à esquerda e à direita dele. Tokens diferentes exigem um número diferente de argumentos; além disso, o local dos argumentos não se limita a “direita” e “esquerda”, mas pode ser, por exemplo, “superior”, “inferior”, “inferior direito”. Também existem tokens compostos que existem desde os tempos antigos , mas os mixfixes receberam um nome especial à medida que as linguagens de programação foram desenvolvidas. Por exemplo, um produto escalar de vetores é indicado da seguinte maneira: $$$\ langle \ cdot, \ cdot \ rangle$ .

Às vezes, os tokens entram em conflito porque não conseguem decidir a quem pertence o argumento escrito entre eles. Então você tem que adicionar colchetes.

Variáveis

Alguns tokens têm um significado que lhes foi atribuído de cima - em algum lugar mais alto do texto ou por links em outros textos. Ou o significado está implícito como geralmente aceito em uma determinada disciplina ou em toda matemática. Por exemplo, o símbolo de mais indica uma operação de adição. Plus - ele está na África plus. No entanto, talvez em algum lugar próximo ao final do seu percurso, você encontre um símbolo de mais com algum significado incomum. Ainda existem tokens (geralmente alfabéticos) que não são explicitamente indicados por nada, eles são chamados de variáveis, dos quais existem vários tipos.

• Parâmetro Essa é uma variável sobre a qual se diz que é significada por alguma coisa, mas não se diz exatamente o que. Se lhe pareceu estranho, você pode ignorá-lo por enquanto e, quando atender aos parâmetros, entenderá imediatamente tudo com exemplos.
• Variável livre. Se uma variável for encontrada na expressão sobre a qual nada é dito, essa variável será chamada livre. A rigor, absolutamente nada pode ser dito. Você tem o direito de perguntar ao autor da fórmula a partir da qual a variável livre é usada. Sinta-se à vontade para perguntar, isso é útil: mesmo que as explicações sejam incompreensíveis, elas o levarão um pouco mais a sério.
• A variável vinculada. Se você não gosta do libertino de variáveis ​​livres, existem várias maneiras de limitar sua liberdade. Você pode adicionar algo à expressão para obter uma nova expressão na qual a variável livre anteriormente está bloqueada. E a nova expressão, diferente da antiga, não dependerá mais dessa variável. Se você está curioso sobre o que é esse "algo", consulte os quantificadores ou uma determinada integral. Tente olhar apenas para a sintaxe, não se aprofundando no significado, mas, você sabe, viciante.

Contexto

Acontece que, olhando para a fórmula, é impossível distinguir uma variável livre de um parâmetro. Isso significa que informações adicionais precisam ser extraídas do contexto, que geralmente é expresso por outras fórmulas ou texto na linguagem humana. Dependendo do contexto, a fórmula pode ter significados diferentes. Se você precisa entender a fórmula, sempre estude o contexto e procure entender.

No entanto, as fórmulas podem existir sem contexto, simplesmente como um objeto sintático no qual as transformações podem ser feitas. Os matemáticos geralmente podem generalizar primeiro - "esquecer" o contexto, depois fazer cálculos, depois "lembrar" o contexto e re-entender o significado das fórmulas obtidas.

Símbolo de igual

O sinal de igual é muito importante. É usado de maneiras diferentes e você precisa ser capaz de distinguir entre eles.

• Avaliação de uma variável por valor. É quando a variável está à esquerda e a expressão à direita. Em algumas disciplinas, nesses casos, em vez de = eles escrevem: = ou mesmo :: =.
• Identidade. À esquerda e à direita, existem algumas expressões, e a pessoa que escreveu isso afirma que ambas as expressões são iguais. O símbolo também é usado aqui. $$$\ equiv$ . Você já pensou no que “igual” significa? Vale a pena discutir, mas pode levá-lo para longe da rota.
• Equação Essa é uma maneira de descrever entidades fundamentalmente novas. Os matemáticos fazem assim: eles pegam várias variáveis ​​livres, constroem expressões sobre elas e as conduzem a uma equação ou mesmo a um sistema de várias equações, para que fiquem ainda mais próximas. E então eles observam como essas variáveis ​​infelizes correm em restrições, formando conjuntos bizarros. E então eles estudam esses conjuntos com grande interesse. (A propósito, sua rota passa pelo território da teoria dos conjuntos, é preciso conhecê-los melhor.) Descrever o conjunto obtido é resolver a equação. As crianças na escola geralmente recebem equações que dão origem a conjuntos muito simples de um elemento, às vezes dois ou nenhum. Mas cientistas adultos nessa questão são grandes artistas. E alguns físicos são capazes de gerar o universo inteiro com uma equação.

Extraindo significado de fórmulas

Algo está escrito, mas entre parênteses, OH. Eles tentaram - e realmente, OH.

O cérebro de um matemático em características físicas não difere fundamentalmente do cérebro de um representante típico da maioria intelectual. Mesmo em termos de memória e velocidade computacional, a diferença não é tão grande. Como os matemáticos conseguem entender fórmulas pesadas e compreendê-las?

Parte da resposta está na capacidade de destacar o principal e abstrair o que não é importante. Como você se lembra, uma expressão consiste em subexpressões. Quando vir uma expressão grande e assustadora, não se apresse em olhar todas as subexpressões de uma só vez, abrindo todas as caixas, caixas, caixas e caixas. : , . , , . , - , , , — , , , .

, , . .

- , - , . . , «- », : « », «», « », « » ..

, , , …
—

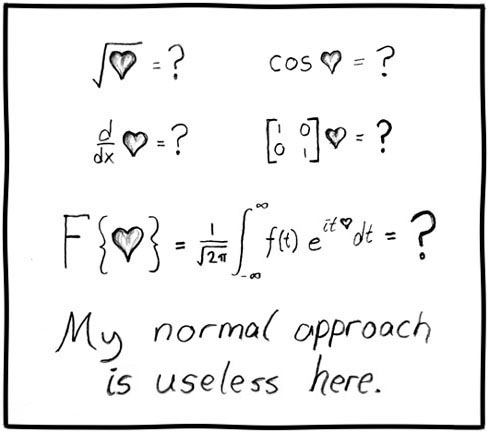
XOR , ?

, . .

, , , . , . , , , , , , .

- , from. , , , , , . , .

, . — ( ), , . , , , . , .

, . , , . , , , .

, , - - . - (, computer science) . , .

— . — .
, -

, . , , . . .

, . . , . , . , , - , . « ». , . , . « ?».

, . $$$a^b$ . : a — , b — , , , . : , .

, .

. «», « » « », . , , . , . , , . , , . , . . : $$$\infty$ . , — . . : ! ! - , , . — , .

• . . .
• . . , ? -.
• . , . -, , , .
• . . , - - .
• , « ». , . , . , .
• , . , . , , .

Voltando à caixa de areia de conjuntos finitos, verifique novamente como você se lembra da notação. Brinque com conjuntos finitos de tamanhos pequenos. Tente aplicar operações básicas a eles. Crie muitos subconjuntos. Se você esqueceu o que é uma bijeção , atualize seu conhecimento em livros didáticos para crianças em idade pré-escolar. Afinal, você conhecia esse conceito desde o período anterior à fala, só então não foi chamado de forma alguma, foi? Verifique se sua intuição está em perfeita harmonia com definições e declarações básicas. Se não for esse o caso, entre em contato com um especialista.

Antes de sair, olhe em volta novamente. Na borda da caixa de areia, você pode ver um canto de ultrafinitivos. Tudo é simples com eles. Diga olá para eles, apenas não diga que você saiu da caixa de areia.

Mais uma vez sobre a notação

quão difícil é viver entre pessoas chatas
disse Michael de três anos
entre os furos
Igor corrigido, trinta e usando óculos

Grupos abelianos -> espaço linear -> operadores -> funcionais no espaço linear. Mas depois de baixar esse ramo, você pode acionar a palavra "funcional" na descrição da funcionalidade do software.

Você já conhece alguns termos matemáticos e continuará aprendendo mais. Tente não usá-los em vão ao se comunicar com especialistas sobre tópicos relevantes. Por exemplo, em vez de expressar "um grupo de métodos", por precaução, é melhor dizer "um conjunto de métodos" ou "um conjunto de métodos" para que ninguém pense que você construiu uma operação em muitos métodos que satisfazem os axiomas do grupo. Se, durante a comunicação informal sobre tópicos matemáticos, você não possui palavras usadas com frequência suficiente devido ao fato de elas se ocuparem com os termos, é melhor usar as chamadas variáveis ​​metassintáticas: “lixo”, “porcaria”, “shnyaga” etc., elas também podem ser emocionalmente pintar com adjetivos: "desajeitado", "liso", "doentio". Não parece tão inteligente, mas é mais provável que você entenda. Depois de algum tempo, você se livrará das palavras feias substitutas e sua fala não causará dor aos filólogos ou matemáticos.

Não use o quantificador universal em vão. O quantificador da universalidade expresso na linguagem comum é representado pelas palavras "sempre", "tudo", "tudo", "todos", "todos", "qualquer", etc. As palavras "nunca", "lugar nenhum" etc. eles também representam esse quantificador, mas com negação, ou seja, "nunca" significa "sempre não". Os matemáticos muitas vezes interpretam as afirmações com o quantificador da universalidade literalmente, após o que, tendo apresentado um contraexemplo, provam o seu erro formal. Você não precisa de estresse extra? Obviamente, há casos em que o quantificador universal pode e deve ser usado.

Em matemática, geralmente há homonímia. É quando uma única palavra ou símbolo designa vários conceitos completamente diferentes. Em primeiro lugar, isso ocorre devido à falta de boas palavras e caracteres. Em segundo lugar, diferentemente das linguagens naturais, muitas vezes conceitos diferentes após alguma generalização acabam sendo praticamente os mesmos. Os matemáticos que percebem que isso é o mesmo, podem experimentar o orgasmo cerebral a partir dessa consciência. Sensações especialmente fortes surgem se o pesquisador fez uma parte significativa do caminho para a conscientização por conta própria. É possível que você também experimente as mesmas sensações fortes. Mas se não, tudo bem, tudo bem também. Sinta-se livre para compartilhar seus sentimentos com especialistas.

Geralmente, a homonímia não dificulta a compreensão, pois os matemáticos cuidadosamente se certificam de que todas as definições sejam rigorosas e corretas.

Lógica

Você precisa trabalhar quase exclusivamente com objetos finais. Isso significa que suas idéias intuitivas sobre lógica provavelmente são suficientes e, mais importante, não levarão a contradições. Apenas para o caso, leia sobre o modus ponens, mesmo que o nome não lhe seja familiar, você definitivamente conhece a essência.

Em geral, a lógica é sobre como fazer novas declarações com base nas existentes. Dê uma olhada ao redor. Em toda parte ao redor de seus ditos: grande, pequeno, óbvio, incompreensível. Você pode assumir que as instruções são divididas em dois tipos: verdadeiro e falso. E aqui estão as figuras! Como você gosta disso?

$$

$$\ int e ^ x = f (u_n)$$

Esta afirmação não é verdadeira nem falsa, não tem sentido (pelo menos do ponto de vista da matemática), porque o que está escrito à esquerda do sinal de igual não é uma expressão. Você pode adicionar dx à integral, mas várias variáveis ​​livres permanecem, por causa das quais a expressão não é uma instrução. Eles terão que significar algo ou conectá-los, para que possamos falar sobre a verdade.

Bem, vamos considerar apenas declarações significativas. Eles deveriam ser verdadeiros ou falsos? Acontece que não. Algumas declarações não podem ser provadas nem refutadas; são chamadas de insolúveis. É improvável que comentários insolúveis sejam encontrados no seu caminho. No entanto, eles certamente encontrarão aqueles sobre a verdade de que até agora nenhuma das pessoas vivas sabe.

Se a última vez em que você não obedeceu e espiou o abismo dos fundamentos da matemática, provavelmente notou que há mais de uma lógica e há muitas diferentes. Felizmente, no seu caminho, esse conhecimento, gerando muitas tristezas, não será necessário. Se você se sentir confortável acreditando que a verdade é sempre a mesma, continue pensando assim.

Teoria das categorias

"Desoxirribonucléico", eu disse. - Este é um ácido. Desoxirribonucléico.
Ele sorriu miseravelmente, ajeitou o pince-nez.
"Ácido", ele repetiu com uma voz interceptada. "Por que ela é assim?"
"Você não pode ligar para ela de outra forma", eu disse com simpatia. "A menos que abreviado como DNA." Sim, você sente falta, Fedya, continue a ler.
"Sim, sim", disse ele. "Eu prefiro sentir falta."
Arkady e Boris Strugatsky - O Conto dos Três

Embora a própria teoria das categorias seja quase tão perigosa quanto a teoria dos conjuntos, precisamos extrair alguns conceitos que se relacionam formalmente a esta seção.

• Classes de adjacência. Essa é uma das maneiras de construir novas estruturas a partir das existentes. Leia a definição, veja alguns exemplos. Se não estiver claro, você pode pular. Mas se você ainda penetrar, receberá algum bônus por entender outras coisas. Por exemplo, sobre o anel $$$\ mathbb {Z} _n$ (isso será necessário um pouco mais tarde) é mais conveniente pensar como uma classe de deduções, e não como o resultado da operação de tirar o restante da divisão. Além disso, a definição escolar de um vetor como um segmento com uma flecha parecerá ridícula e até errada para você. Você pode ensinar aos seus amigos que um vetor não é um segmento, mas uma classe de segmentos.
• Morfismos. Morfismo é alguma relação entre um par de objetos. Você conhece um desses tipos de morfismo a partir dos três anos de idade - essa é uma bijeção entre conjuntos finitos. Leia a definição de isomorfismo e perceba que este é um caso mais geral de bijeção. Entenda bem, isso é importante. Se necessário, consulte um especialista. Além disso, você pode ler sobre o homomorfismo (para não confundir com o homeomorfismo!). Se houver homomorfismofobia ou outras dificuldades, você pode pular.

Em geral, toda a teoria das categorias é a seção mais abstrata da matemática; não há nada lá, exceto pequenas coisas e flechas. Apesar de algum perigo para a psique, a teoria da categoria pode ser recomendada para a terapia de substituição de outros tipos de dependência. No entanto, não se automedique, na sua cidade, provavelmente, existem especialistas disponíveis.

Álgebra

Honestamente, não suspeitava que há mais de quarenta anos estou falando em prosa.
Jean-Baptiste Moliere - Comerciante na nobreza

O nome da disciplina deve ser familiar para você da escola. De fato, a álgebra trabalha com estruturas algébricas, e em uma escola apenas números inteiros e racionais passam de estruturas, bem como (de uma forma fortemente truncada) reais. A boa notícia é que agora você não precisa resolver as equações algébricas que o atormentaram na escola. Se algum surgir no seu caminho, então já está decidido. Se alguma coisa, o computador conta para você, é de ferro. Você precisa se familiarizar com apenas algumas estruturas algébricas específicas.

Antes de tudo, é importante entender claramente o conceito de estrutura algébrica . Leia a definição, entenda bem. Revise a definição do grupo . No carregamento, estão as definições de todos os subgrupos, como monóides, semigrupos e grupóides. Leia-os também, mas não se preocupe em lembrar. Você só precisa de grupos. Em seguida, estude a definição de um anel e um campo .

Atenção! Evite lugares onde estruturas com uma transportadora infinita são explicitamente declaradas. Ainda precisamos de alguns desses objetos sem fim, mas você os conhece. Ou seja: um anel de números inteiros $$$\ mathbb {Z}$ campo de números racionais $$$\ mathbb {Q}$ e o campo de números reais $$$\ mathbb {R}$ . Brinque com eles, lembre-se das regras da escola como “o valor não muda da alteração dos termos dos termos” e justifique por eles o fato de que essas estruturas são realmente anéis / campos. Explique por que números inteiros não formam um campo.

Como o objetivo final deste guia é precisamente a criptografia elíptica, você terá que se familiarizar com o conceito de um polinômio sobre um campo . Para não estudar as definições gerais, entre em contato com um especialista para que ele informe apenas o que é relevante para o objetivo de sua viagem.

Se você gosta mais de geometria do que de álgebra, pode ver as curvas elípticas acima do campo $$$\ mathbb {R}$ . Mas lembre-se de que, apesar do nome, esses objetos visuais estão completamente distantes do seu caminho.

Por uma questão de interesse, você também pode meditar nas definições de outras estruturas algébricas: álgebra (sim, álgebra é uma estrutura algébrica; não se assuste, isso não é recursão, mas apenas homonímia), espaço vetorial (linear) ...

Retorne à rota. Você está aguardando o campo final . Leia um artigo sobre eles. Na verdade, nem tudo é necessário. Esse é outro caso em que, para economizar esforço, é melhor procurar imediatamente o aconselhamento de um especialista. Perceba a classificação de campos finitos, é simples. A propósito, será interessante saber por que os campos finitos também são chamados de campos de Galois. Lembre-se do que você fez em 20 anos e tenha vergonha.

Se você gosta de trollar e aprecia suas habilidades, tente reconhecer os bourbacistas e anti-bourbacistas no fórum temático e reuni-los.

Teoria da informação

Se você nasceu depois de 1970, provavelmente foi informado no ensino médio sobre bits e bytes. Os bytes na ciência básica não são particularmente necessários, mas o conceito de um pouco precisa ser conhecido claramente. Dê uma olhada no livro, se necessário.

Conte ou descubra no livro quantas seqüências totais de bits de um determinado comprimento existem. Brinque com o alfabeto, codificando as letras em uma sequência de bits. Pense ou leia no livro como codificar números inteiros. Considere o que é útil na teoria da informação é o logaritmo da base dois.

Teoria da probabilidade

Qualquer um que tenha uma fraqueza nos métodos aritméticos para obter números aleatórios é pecador, sem dúvida.
John von Neumann

O mal-entendido da teoria das probabilidades e sua aplicação a questões práticas é a fonte mais importante de erro humano. Este é um tópico muito importante, tente dedicar algum tempo para se familiarizar com o básico. Não necessariamente no momento, porque para o objetivo final de nossa rota, apenas uma de suas subseções aplicadas é suficiente - geração aleatória de números.

Agora basta que você perceba que a questão da geração de números aleatórios é muito complicada, institutos inteiros vêm lidando com ela há décadas. Mesmo determinar o que é a chance é muito complicado. Você não pode simplesmente pegar e pegar um número aleatório. Infelizmente, existe uma armadilha de idioma que dificulta a compreensão do tópico. A palavra aleatório, assim como seu equivalente russo, "aleatório", embora em menor grau, signifique essencialmente "horrível", enquanto que para muitas aplicações, especialmente para criptografia, você precisa escolher muito longe de tudo.

Se você entendeu bem a teoria da probabilidade, consulte um especialista. Se o tempo permitir, vá embora para examinar a interpretação multimaterial (Everett) da mecânica quântica. Não se empolgue, você está esperando em casa.

Teoria da computabilidade

É possível fazer esse compilador sempre avisar que o programa pode entrar em ciclos?

Você não precisará desta seção no momento. É simplesmente útil perceber que, para nenhuma função matematicamente definida, existe um algoritmo que a calcula. Se você sentir a força em si mesmo, faça uma excursão pela história do problema, tente entender as definições e os resultados básicos. Não sobrecarregue, este tópico é opcional.

Apenas para reduzir o estresse da realização de sua própria ignorância, informarei que a pergunta submetida à epígrafe foi feita por um respeitado professor de física e matemática, cuja esfera de interesses se distancia da ciência da computação. Se você entende a situação anedótica, sua excursão foi útil. Incentive-se.

Teoria da complexidade

Infelizmente, a ciência clássica evoluiu para que a teoria da complexidade, estritamente falando, se baseie na teoria dos limites da análise matemática. Tudo isso porque matemáticos egoístas não cuidaram de você. Eles abordaram a complexidade, já de pé sobre os ombros dos gigantes, e usaram as ferramentas que eles próprios possuíam com perfeição. Para nossos modestos objetivos, foi possível construir nossa própria teoria pequena da complexidade, que até os ultrafinitivos gostariam. Mas, por exemplo, não tenho força nem motivação para concluir a construção de uma parte justa da paisagem. Portanto, você ainda precisa recorrer ao que é chamado de palavra matan.

Análise matemática

Eu não sou um botânico, eu apenas amo matan.

Leia a definição do limite de sequência (você não precisa de um limite de função). Substitua todas as expressões como "tal e tal espaço" por "um conjunto de números reais", matemáticos gostam de generalizar, mas você não precisa disso. Certifique-se de poder analisar expressões que tenham uma palavra $$$\ lim$ . Provavelmente, você terá dificuldades, isso é normal. Acredite, o conceito de limite é muito intuitivo, você só precisa estimular a parte correspondente da sua intuição. Peça a um especialista para comentar o texto da definição. Desenhe gráficos, brinque com sequências simples. Se o tempo permitir, faça uma excursão para observar o segundo limite maravilhoso.

Mesmo se você não tiver um entendimento completo do limite, poderá prosseguir imediatamente para a notação O. Você só precisa de “O” grande , mas a carga fica “O” pequena e todos os tipos de teta e ômega. Não trabalhe demais, para começar, você só precisa entender aproximadamente o que eles são $$$O (1), O (N), O (\ log N)$ . Descubra, mas tente adivinhar por que $$$O (\ log N)$ apenas um logaritmo, não um logaritmo por algum motivo. Então descanse um pouco e segure em suas mãos $$$O (N ^ 2)$ e $$$O (2 ^ N)$ . Olhe para $$$O (N ^ k)$ (lembre-se do contexto: aqui N é uma variável, k é um parâmetro). Pense por que eles falam sobre crescimento polinomial quando $$$N ^ k$ - apenas um monômio, isto é, um caso especial de um polinômio, mas eles não colocam muitos polinômios completos sob O (Mesmo que você não fale latim, provavelmente já adivinhou que um polinômio é o mesmo que um polinômio, e um monômio é um monômio.) Dica: o motivo é muito semelhante ao que “é simplesmente um logaritmo” e não “qual logaritmo para o chão ". Entre em contato com um especialista para esclarecer esses problemas. Aprenda a comparar esses "O's" entre si.

Nota: o-notation é um exemplo raro quando a notação matemática não é consistente. No registro $$$f (N) = O (N)$ o sinal de igual é usado, enquanto implica outra coisa, a saber: “função $$$f (N)$ pertence à classe $$$O (N)$ " Ou seja, um sinal assimétrico deve ser usado $$$\ em$ mas essa é a tradição. Bem, agora você vê que os matemáticos não são sem pecado. Talvez se torne um pouco mais fácil para você perceber esse fato.

Teoria da complexidade computacional - continuação

Logaritmo - uma função, em princípio, limitada.

Após uma pequena inserção do matan, você pode facilmente dominar a escala para medir a complexidade assintótica. A complexidade dos algoritmos é geralmente medida em termos de tempo de execução: às vezes eles falam sobre o tempo usual medido usando o relógio (bem, quando será carregada esta guia do navegador?), Às vezes sobre o número de ciclos do processador ou etapas de um computador abstrato. Aqueles que são mais inclinados à física preferem medir a complexidade em unidades de energia, por exemplo, na quantidade de diesel consumida por uma máquina de Turing. Todos esses métodos de medição são aproximadamente equivalentes. É importante saber como o tempo gasto (ou energia) depende do tamanho dos dados de entrada do algoritmo. Este é N em "O" grande na estimativa assintótica e é o tamanho dos dados de entrada, expressos em bits. Os especialistas concordaram em considerar que, se a complexidade do algoritmo não crescer mais rápido que um polinômio, será "fácil", caso contrário, "difícil". É apropriado voltar um pouco e lembrar como comparar funções entre si em termos de frieza, isto é, em termos da velocidade do crescimento assintótico.

Se você perceber que a declaração feita na epígrafe é falsa, incentive-se. Ele foi entregue por um professor universitário em métodos computacionais. Conhecendo esse contexto, pense especificamente no que ele tinha em mente.

Funções unidirecionais. Leia a definição. . , , , .

, , . , . , . ?

«». « », — « ». <…> . <...> . , , .
—

, . ! , , (, , ). , . - . , . ? Bom , ?

Agradecimentos

, . Shapelez .