A justificativa matemática da inadequação de descer a escada rolante no metrô

Ao contrário das regras de uso do metrô, para economizar tempo, cada um de nós desceu a escada rolante pelo menos uma vez na vida. À primeira vista, parece que isso é absolutamente lógico e correto: se você quiser sair mais rápido - tente estar na plataforma o mais cedo possível. No entanto, quase imediatamente surge o seguinte cenário: você voa de cabeça para baixo na escada rolante, desce para a plataforma e as portas do carro se fecham bem na frente do seu nariz. Enquanto você aguarda o próximo trem - as pessoas que subiram na escada rolante ao mesmo tempo em que você tem tempo para ficar quieto, descem e pegam o próximo trem. Nesse caso, não há ganho. Então, quão racional é descer a escada rolante e vale a pena fazê-lo? Corro para agradá-lo - a resposta é encontrada! Abaixo, há uma justificativa matemática para a inexpedibilidade (sim, NÃO) para descer a escada rolante no metrô.

Declaração de tarefa

Antes de recorrer ao raciocínio matemático, vale ressaltar que, é claro, não sou o primeiro a pensar sobre esse assunto. Na Internet, você pode encontrar um número suficiente de artigos e até notícias de canais federais sobre esse assunto. No entanto, cada vez que a essência desse tipo de experimento consiste na descida usual da escada rolante, com a comparação subsequente do tempo ganho com o tempo da pessoa em pé na escada rolante. Um pouco melhor se os autores estiverem tentando avaliar a eficácia da descida. Ainda melhor se eles ainda fornecerem estatísticas. Quanto às estatísticas, a propósito, direi um agradecimento especial um pouco mais baixo. Em conexão com a falta de clareza desses experimentos e a falta de conclusões práticas, fui concebido e, posteriormente, realizado uma análise do processo em andamento.

E assim, formulamos as condições do problema e denotamos as restrições:

1. O experimento (mental) envolve duas pessoas que se aproximam da escada rolante ao mesmo tempo em um momento aleatório no tempo e não têm idéia de onde o trem está.
2. Uma dessas pessoas está de pé em uma escada rolante e passa um tempo descendo. $$ igual ao tempo de movimento da escada rolante.
3. O segundo acelera a escada rolante, aumentando sua velocidade em $$ vezes, reduzindo assim o tempo de descida pelo mesmo número de vezes: $$ .
4. Efetiva é considerada uma descida acelerada, o que levou ao fato de que a pessoa que está na escada rolante não tem tempo para entrar no trem, na qual a pessoa que está escapando na escada rolante tem tempo para embarcar.
5. Denotar por $$ - a probabilidade de uma descida efetiva. Então, de acordo com o equilíbrio de Nash, uma pessoa está pronta para arriscar e descer a escada rolante apenas se a probabilidade de uma descida efetiva for maior ou igual à probabilidade de uma descida ineficaz ou parada no local, ou seja, 0,5. Se a probabilidade de uma descida efetiva for maior ou igual a 0,5, a decisão de descer a escada rolante será considerada apropriada . Se for menor que 0,5 - impraticável .
6. Negligenciamos o fato de que, na vida real, como regra geral, é necessário ir mais longe até o carro depois de sair da escada rolante ou esperar que as pessoas saiam do carro, os trens circulam em intervalos variáveis ​​e por algum tempo ficam imóveis antes de abrir e fechar as portas, isto é, assumiremos que, no momento em que sair da escada rolante, o trem estiver na estação, suas portas estarão abertas e o participante do experimento acabará instantaneamente no carro, o próprio trem abre (fecha) as portas e chega (sai) instantaneamente à estação (da estação) e dnomomentno.

Progresso da decisão

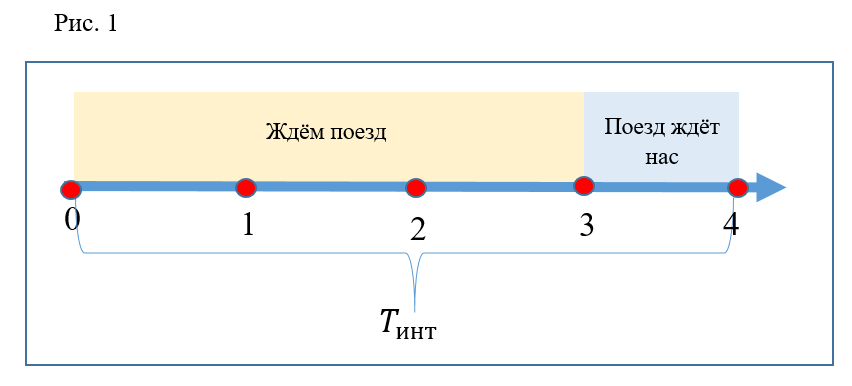
Vamos desenhar o eixo do tempo (Fig. 1). Todo o eixo terá intervalos consecutivos entre os trens. A seguir, apenas um intervalo será considerado. Divida o intervalo mostrado em 4 segmentos iguais. O ponto 0 neste eixo corresponde ao momento em que o trem sai da estação. O ponto 3 corresponde à chegada do comboio e à abertura das portas. Ponto 4 - fechando as portas e partida do trem. Assim, para conveniência da representação gráfica e dos cálculos, o intervalo entre os trens é contado entre os momentos de partida dos trens da estação. Os três primeiros segmentos são o tempo que os passageiros são forçados a esperar pelo trem que chega. O quarto segmento é o tempo de parada do trem, quando os passageiros podem embarcar. Coloque também esse tempo $$ (tempo de descida na escada rolante) é igual a dois segmentos. Coeficiente $$ igual a 2, ou seja, o tempo de descida correndo 2 vezes menos e igual a um segmento.



Agora, para determinar a probabilidade $$ , descubra em que período a decisão de fazer jogging levará ao fato de que a descida será eficaz. Por exemplo, se nossos participantes abordarem a escada rolante no momento 0, o primeiro estará na plataforma no momento $$ (Fig. 2), e o segundo anterior, no momento $$ . Mas, como pode ser visto na figura, em nenhum desses momentos há um trem na estação, o que significa que correr para baixo era ineficiente.



Considere outro caso (Fig. 3): os participantes do experimento se aproximam da escada rolante no momento 2. Como no caso anterior, o primeiro estará na plataforma no momento $$ e o segundo anterior, no momento $$ . Mas é óbvio que nos dois momentos o trem está na estação. Portanto, ambos terão tempo para embarcar no mesmo trem, portanto, correr para baixo era igualmente ineficiente.



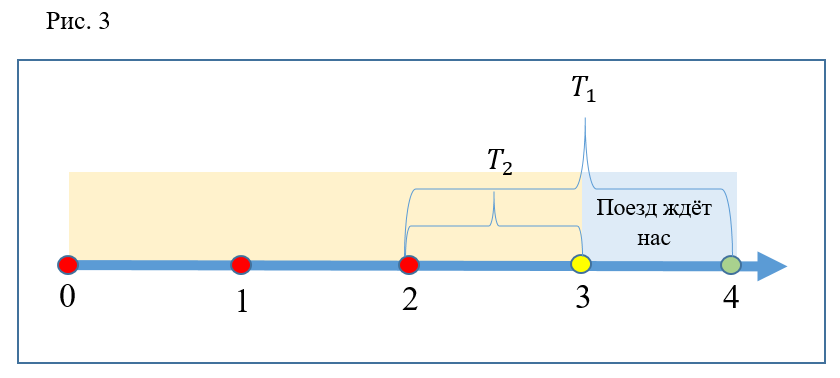
Além disso, é fácil entender que a qualquer momento no intervalo de 2 a 3, é eficaz decair, pois a pessoa que escapou sempre consegue embarcar no trem, e não o que escapou. Se você escolher pontos de tempo entre 3 e 4, ambos os participantes estão atrasados ​​para o trem e são forçados a esperar pelo próximo juntos, ou seja, correr novamente é ineficaz.

Acontece que em quatro períodos condicionais de tempo, é eficaz diminuir apenas se os participantes se aproximarem da escada rolante entre 2 e 3 vezes (Fig. 4). A probabilidade de entrar nele é de 1/4. Consequentemente, sob as condições determinadas da tarefa, a decisão de atropelar é impraticável, pois o segundo participante tem mais probabilidade (com probabilidade de 3/4) de correr em vão e será forçado a esperar o trem junto com o primeiro, que desceu mais tarde.



As seguintes observações serão completamente justas:

1. Intervalos entre trens podem diminuir e aumentar. O tempo de estacionamento pode aumentar e o tempo de espera pode diminuir (com o mesmo intervalo) e vice-versa.
2. A velocidade da escada rolante para baixo é constante, mas o tempo de descida pode variar, pois as estações podem ser mais ou menos profundas.
3. O segundo participante pode muito bem executar não 2, mas 3 ou até 4 vezes mais rápido que a escada rolante.

Para avaliar o impacto das mudanças nos fatores acima, é necessário derivar a relação entre esses valores e a probabilidade de subir na escada rolante no momento em que for eficaz a sua queda.

Para fazer isso, descreveremos outro caso (Fig. 5). Deixamos inalterados todos os dados originais, com exceção de um: coeficiente $$ aumente para 4. Ou seja, o segundo participante estará na parte inferior 4 vezes mais rápido que o primeiro. Para maior comodidade da imagem, dividimos nosso intervalo em 8 partes iguais. Assim, o tempo de descida na escada rolante agora é igual a 4 segmentos, o trem para às duas, o tempo de espera é 6 e o ​​tempo de descida para correr sozinho. Não é difícil descobrir que agora a duração do intervalo de tempo “efetivo” (de 4 a 7 pontos no tempo) é 3. Ou seja, a probabilidade $$ igual a 3/8. Isso já é mais do que no primeiro caso, mas não realizamos essas mudanças para avaliar a probabilidade.



Com base nas Figuras 4 e 5, é óbvio que o comprimento do segmento "efetivo" é $$ . Divida pela duração do intervalo e obtenha a probabilidade $$ onde $$ .
Realizamos uma série de transformações: $$$$ .
A fórmula final: $$ .

Com base nesta fórmula, várias conclusões fundamentais podem ser tiradas ao mesmo tempo:

1. O valor da probabilidade não é afetado por alterações no tempo de estacionamento e no tempo de espera do trem se o intervalo total não mudar (fig. 6).
   
   
   
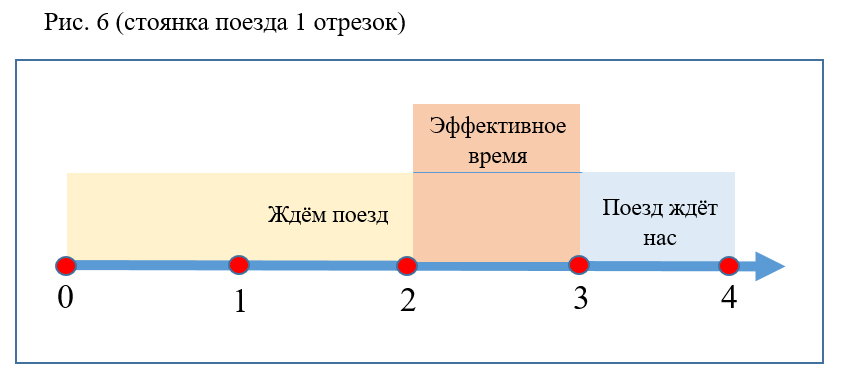
2. Quanto maior o intervalo entre trens, menor a probabilidade P (Fig. 7).
   
   
   
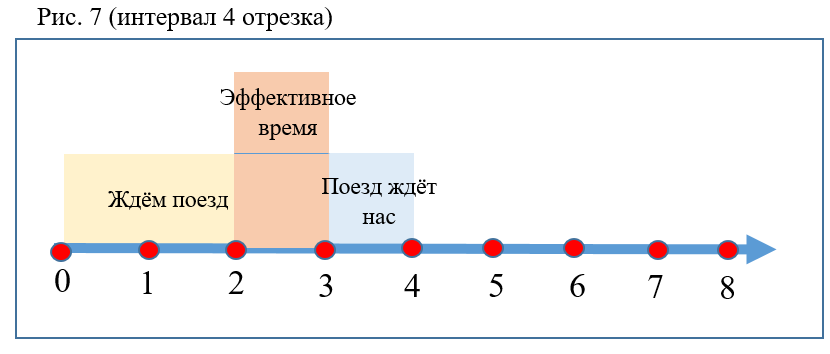
3. A probabilidade aumenta se a proporção do tempo de descida na escada rolante para o intervalo e / ou o coeficiente K aumentar.
   

Verificação de fidelidade

Agora vamos ver quão verdadeira é a fórmula derivada?

Para verificar a exatidão da fórmula, recorremos às estatísticas, que foram muito úteis em 2014 pelo correspondente do The Village. Expresso meu reconhecimento e, naturalmente, no final do artigo, deixarei um link para o artigo original. Também é bom que as estatísticas sejam apresentadas como infográficos visuais.

Experiência 1. Estação de metrô Chekhovskaya



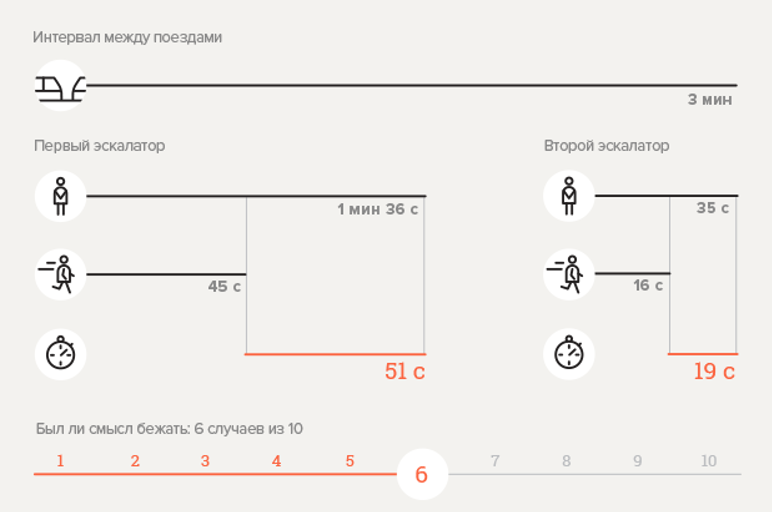
Calcular a probabilidade $$ .
Aqui $$ ; $$ ; $$ ; $$ ; $$ .

O resultado obtido, aparentemente, diverge dos dados experimentais. A fórmula está errada? Não! Pode ser visto no infográfico que a descida para a estação envolve uma viagem em duas escadas rolantes; no entanto, o tempo de transição entre elas não é levado em consideração. Se, por confiabilidade, assumirmos que a transição leva pelo menos 30 segundos, substituindo um novo valor $$ nós obtemos: $$ ; $$ , que está muito mais próximo do resultado experimental. Também é importante notar que o experimento forneceu apenas 10 repetições. Ao aumentar o número de repetições, é possível obter uma coincidência quase completa dos dados calculados com os resultados obtidos durante o experimento.

Experiência 2. Estação de metrô "Victory Park"



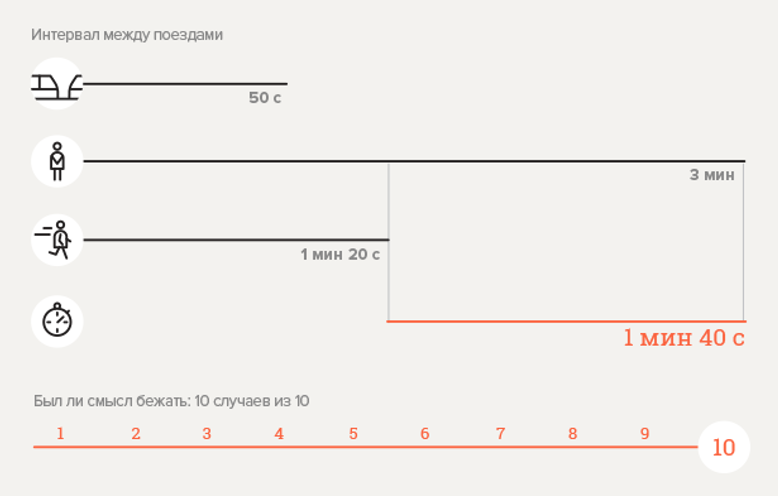
Calcular a probabilidade $$ .
Aqui $$ ; $$ ; $$ ; $$ ; $$ .
Pode-se ver que temos uma probabilidade maior que uma. Mas não há contradição aqui. Se você observar a forma geral da fórmula, torna-se óbvio que, quando o tempo de descida na escada rolante for igual ao intervalo entre trens, um aumento na velocidade de pelo menos 2 vezes aumentará a probabilidade de que a descida acelerada seja efetiva igual a 0,5. Se o tempo de viagem da escada rolante for maior que o intervalo, com o mesmo coeficiente $$ a probabilidade de pegar um trem mais cedo só aumentará. Finalmente, se o tempo de descida na escada rolante for 2 ou mais vezes o intervalo, a pessoa que corre em 100% dos casos chegará a tempo para o trem pelo qual o restante da escada rolante não terá tempo. É esse efeito que observamos neste experimento: o correspondente concluiu que ele desapareceu em 10 dos 10 casos.

Experiência 3. Estação de metrô Park Kultury



Calcular a probabilidade $$ .
Aqui $$ ; $$ ; $$ ; $$ ; $$ .

Mais uma vez um erro? Nem um pouco. Pode-se observar que, como mencionado acima, o tempo de descida na escada rolante é 2 vezes o intervalo entre os trens. O tempo de execução é 2 vezes menor. Acontece que toda descida deve ser eficaz. Mas não se esqueça que, antes de iniciar a discussão, assumimos o fechamento instantâneo de portas e, pelo menos, a partida instantânea do trem da estação. Se você imaginar uma opção como na Figura 8, fica claro que na vida real uma pessoa em fuga pode não ter tempo para sentar no ponto 1 (por exemplo, o trem partirá um pouco mais cedo) e no ponto 2 o trem, pelo contrário, atrasará um pouco, e então uma pessoa que não corre, senta-se nela, juntamente com uma pessoa que corre atrasada, correndo no trem anterior.



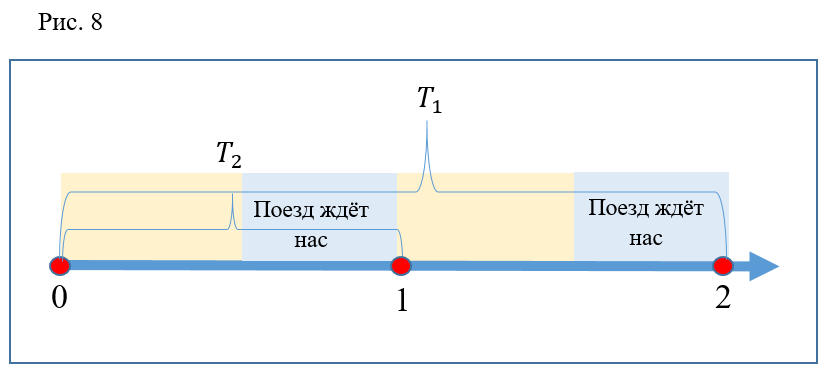
Suponho que em ambos os tempos "ineficazes" aconteceu. Há todos os motivos para argumentar que, com um aumento no número de repetições do experimento, a porcentagem de execuções "efetivas" tenderá a 100%.

Conclusões

Agora que, com base nos dados experimentais disponíveis, foi possível confirmar a exatidão da fórmula, vamos analisá-la e tirar conclusões. Desde o início, concordamos que consideraríamos a decisão de correr para baixo se a probabilidade de uma descida efetiva for maior ou igual a 0,5. Ou seja, literalmente, se tivermos certeza de que pelo menos metade dos casos corremos por um bom motivo, vale a pena correr o risco e correr, porque, se nos atrasarmos, praticamente não perderemos nada. Com base no exposto, reescrevemos a fórmula de probabilidade da seguinte maneira: $$ .

É interessante que, como já descobrimos, faz sentido sempre correr quando $$ . Ao mesmo tempo, também é verdade que se $$ , não importa o quão rápido você corra, a probabilidade de pegar um trem mais cedo é menor que 0,5, pois é óbvio que $$ nunca será maior que ou igual a 1.

Agora vamos dar uma olhada na velocidade do correspondente. Em média, é cerca de 2 vezes a velocidade da escada rolante (o tempo de descida é 2 vezes menor). Em geral, esses dados coincidem com os resultados de minhas próprias experiências (não vejo o sentido de trazê-las). Como regra, já é difícil desenvolver uma velocidade com um coeficiente K de pelo menos 3: há muitos que querem correr em uma escada rolante real e, além disso, as pessoas que estão à sua esquerda ou seus pertences (bolsas, malas) podem interferir. Meios $$ e $$ . Ou seja, uma decisão de acelerar será apropriada somente se a proporção $$ não inferior a 1. E isso só é possível quando o tempo de descida na escada rolante para baixo não for menor que o intervalo entre os trens. Em um metrô real, onde o intervalo médio entre os trens é de 2 minutos, nem todas as estações podem ter uma longa descida. Como regra, mesmo no metrô de São Petersburgo, o tempo de viagem da escada rolante é de cerca de 1 minuto e 30 segundos, ou seja, 0,75 vezes menos que o intervalo. A seguir, segue a conclusão fundamental muito óbvia e mais importante: se você tem certeza de que a escada rolante nesta estação se move menos que o intervalo entre os trens, não é prático percorrê-la.

PS Leve em consideração o fato de que esta tarefa não leva em consideração a necessidade de entrar em um carro específico. Trata-se exclusivamente de entrar na plataforma e depois embarcar no trem.

Fonte de dados experimental: The Village . Mais uma vez obrigado!