O conjunto de dados usado a seguir é retirado de uma competição de kaggle já aprovada a
partir daqui .
Na guia Dados, você pode ler a descrição de todos os campos.
Todo o código fonte
está no formato laptop
aqui .
Carregamos os dados, verifique se geralmente temos:
import numpy as np import pandas as pd dataset = pd.read_csv('../input/ghouls-goblins-and-ghosts-boo/train.csv')
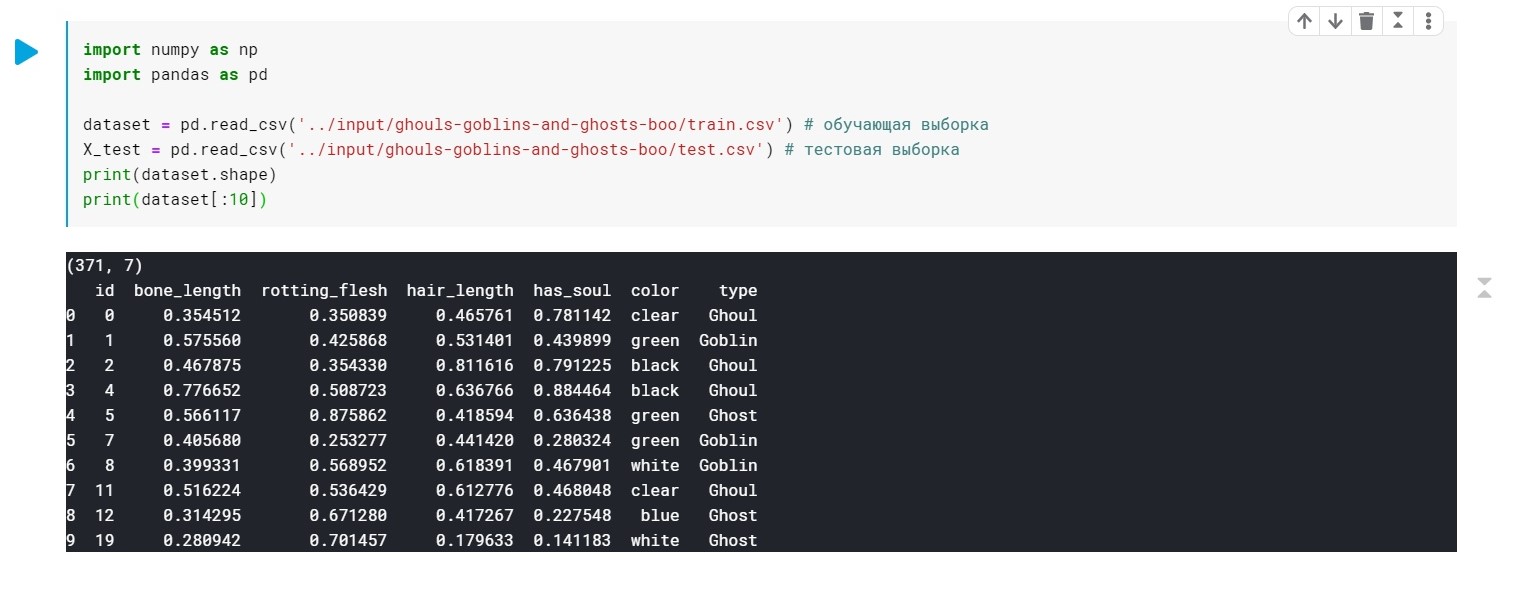
Os valores do campo de tipo (Ghoul, Ghost, Goblin) são simplesmente substituídos por 0, 1 e 2.
Cor - também precisa ser pré-processado (precisamos apenas de valores numéricos para construir o modelo). Usaremos LabelEncoder e OneHotEncoder para isso.
Mais detalhes .
from sklearn.preprocessing import LabelEncoder, OneHotEncoder labelencoder_X_1 = LabelEncoder() X_train[:, 4] = labelencoder_X_1.fit_transform(X_train[:, 4]) labelencoder_X_2 = LabelEncoder() X_test[:, 4] = labelencoder_X_2.fit_transform(X_test[:, 4]) labelencoder_Y_2 = LabelEncoder() Y_train = labelencoder_Y_2.fit_transform(Y_train) one_hot_encoder = OneHotEncoder(categorical_features = [4]) X_train = one_hot_encoder.fit_transform(X_train).toarray() X_test = one_hot_encoder.fit_transform(X_test).toarray()
Bem, neste momento nossos dados estão prontos. Resta treinar nosso modelo.
Primeiro aplique o
Adagrad :
Em essência, esta é uma modificação da descida do gradiente estocástico, sobre a qual escrevi da última vez:
habr.com/en/post/472300Este método leva em consideração o histórico de todos os gradientes anteriores para cada parâmetro individual (a ideia de dimensionar). Isso permite reduzir o tamanho da etapa de aprendizado para parâmetros com um grande gradiente:
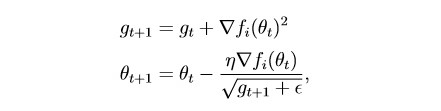
g é o parâmetro de escala (g0 = 0)
θ - parâmetro (peso)
epsilon é uma pequena constante introduzida para impedir a divisão por zero
Divida o conjunto de dados em 2 partes:
Amostra de treinamento (trem) e validação (val):
from sklearn.model_selection import train_test_split x_train, x_val, y_train, y_val = train_test_split(X_train, Y_train, test_size = 0.2)
Um pouco de preparação para o treinamento do modelo:
import torch import numpy as np device = 'cuda' if torch.cuda.is_available() else 'cpu' def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step
Modelo de auto-treinamento:
from torch import optim, nn model = torch.nn.Sequential( nn.Linear(10, 270), nn.ReLU(), nn.Linear(270, 3)) lr = 0.01 n_epochs = 500 loss_fn = torch.nn.CrossEntropyLoss() optimizer = optim.Adagrad(model.parameters(), lr=lr) train_step = make_train_step(model, loss_fn, optimizer) from sklearn.utils import shuffle for epoch in range(n_epochs): x_train, y_train = shuffle(x_train, y_train)
Classificação do modelo:
Aqui, além das camadas, temos apenas 2 parâmetros configuráveis (por enquanto):
taxa de aprendizado e n_epochs (número de épocas).
Dependendo de como combinamos esses dois parâmetros, podem surgir 3 situações:
1 - está tudo bem, ou seja, o modelo mostra baixa perda na amostra de treinamento e alta precisão na validação.
2 - underfitting - grande perda na amostra de treinamento e baixa precisão na validação.
3 - sobreajuste - baixa perda na amostra de treinamento, mas baixa precisão na validação.
Com o primeiro, tudo está claro :)
Com o segundo, parece, também - experimentar a taxa de aprendizado e os n_epochs.
E o que fazer com o terceiro? A resposta é simples - regularização!
Anteriormente, tínhamos uma função de perda do formulário:
L = MSE (Y, y) sem termos adicionais
A essência da regularização é precisamente que, adicionando um termo à função objetivo, “afina” o gradiente se ele for muito grande. Em outras palavras, impomos uma restrição à nossa função objetivo.
Existem muitos métodos de regularização. Mais sobre L1 e L2 - regularização:
craftappmobile.com/l1-vs-l2-regularization/#_L1_L2O método Adagrad implementa a regularização L2, vamos aplicá-lo!
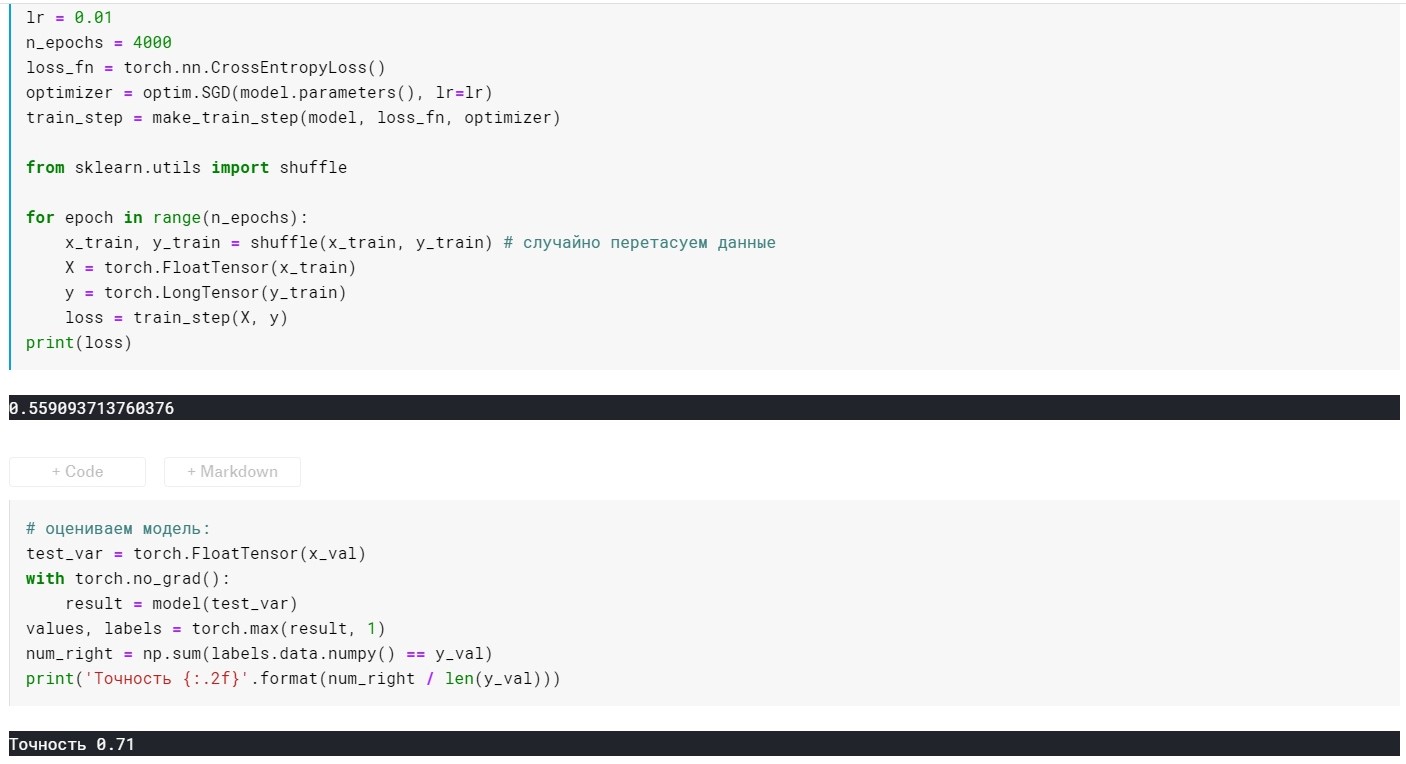
Primeiro, para maior clareza, observamos os indicadores do modelo sem regularização:
lr = 0,01, n_epochs = 500:
perda = 0,44 ...
Precisão: 0.71
lr = 0,01, n_epochs = 1000:
perda = 0,41 ...
Precisão: 0.75
lr = 0,01, n_epochs = 2000:
perda = 0,39 ...
Precisão: 0.75
lr = 0,01, n_epochs = 3000:
perda = 0,367 ...
Precisão: 0.76
lr = 0,01, n_epochs = 4000:
perda = 0,355 ...
Precisão: 0.72
lr = 0,01, n_epochs = 10000:
perda = 0,285 ...
Precisão: 0.69
Aqui você pode ver que em 4k + eras - o modelo já está super ajustado. Agora vamos tentar evitar isso:
Para fazer isso, adicione o parâmetro weight_decay ao nosso método de otimização:
optimizer = optim.Adagrad(model.parameters(), lr=lr, weight_decay = 0.001)
Com lr = 0,01, m_epochs = 10000:
perda = 0,367 ...
Precisão: 0.73
Às 4000 eras:
perda = 0,389 ...
Precisão: 0.75
Ficou muito melhor, mas adicionamos apenas 1 parâmetro no otimizador :)
Agora considere o SGDm (esta é uma descida gradiente estocástica com uma pequena extensão - heurísticas, se você preferir).
A conclusão é que o
SGD atualiza os parâmetros fortemente após cada iteração. Seria lógico “suavizar” o gradiente usando gradientes de iterações anteriores (a idéia de inércia):
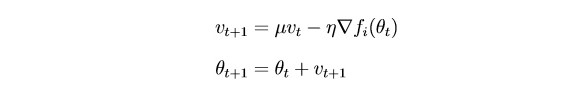
θ - parâmetro (peso)
µ - hiperparâmetro de inércia
SGD sem parâmetro de momento:
SGD com parâmetro de momento:
Acabou não muito melhor, mas o ponto aqui é que existem métodos que usam imediatamente as idéias de escala e inércia. Por exemplo, Adam ou Adadelta, que agora mostram bons resultados. Bem, para entender esses métodos, acho necessário entender algumas idéias básicas usadas em métodos mais simples.
Obrigado a todos pela atenção!