Curva de Bezier a serviço dos economistas do trabalho

(a representação resultante de uma tentativa de desenvolver uma justificativa para os salários estabelecidos na empresa)

Em vez de anotação

Se você já pensou na necessidade de justificar o tamanho da parte salarial dos salários dos funcionários da empresa, precisava de clareza e simplicidade ao tomar essas decisões, então você não está sozinho e com o material sob o corte para você. Uma tentativa modesta de implementar um sistema de justificação salarial em uma empresa usando modernos mecanismos de avaliação integrados para derivar um sistema de classificação de pontos e curvas de Bezier como base para a conversão de pontos nos salários resultantes será apresentada aqui.

Breve declaração do problema

A estrutura da remuneração total de uma empresa moderna é diversa, de forma generalizada, pode conter vários componentes (Fig. 1). Nesta publicação, estaremos interessados ​​no salário básico. Pode-se notar também que, no processo de trabalho, na maioria das vezes, as estruturas foram consideradas onde prevalecem os salários baseados no tempo.


Figura 1. A estrutura da remuneração total.

Gostaria especialmente de observar que, ao considerar o problema, a visão dos autores foi voltada, em grande parte, para o pessoal que não é de produção, cujo trabalho é muito difícil de medir e digitalizar.

O salário líquido do tempo não é um fator estimulante, mas se o princípio da justiça e transparência for violado, poderá afetar significativamente a diminuição da motivação. A violação do princípio da justiça é expressa do seguinte modo:

1. Atos locais normativos sobre pagamento são formais e não determinam o estabelecimento e a mudança reais de salários.
2. A grade tarifária é construída para que um especialista sem uma categoria possa receber tanto quanto o chefe do departamento (desfoque de malha).
3. Grupos de posts, unidos na categoria de pagamentos, podem diferir significativamente na complexidade do trabalho realizado.
4. Os salários dependem da divisão em que o funcionário trabalha, e não da complexidade de seu trabalho.

Também introduzimos alguns termos adicionais:

A classificação é uma maneira de definir uma taxa salarial com base em uma avaliação das atividades de cada funcionário (ou local de trabalho) de acordo com critérios uniformes, distribuídos de acordo com sua importância (valor) para a organização.

Em outras palavras:

- trata-se de uma divisão de todas as posições na empresa por categorias da mais alta para a mais baixa, cada uma das quais recebe um salário específico, ou “bifurcação” de salário, que determina as tarifas tarifárias mínima e máxima para cada posição.

Nossa legislação trabalhista não exige pessoal e o cronograma tarifário para estruturas comerciais, e ambos são necessários antes de tudo pelo próprio empregador como uma ferramenta para gerenciar recursos trabalhistas.

Os desenvolvimentos nesta área, trabalhos científicos de autores famosos, estão indiscutivelmente presentes. Além disso, o leque de candidatos é amplo. O mais famoso, talvez, é o desenvolvimento do Hay Group . Ainda bem, não vou criticar e trazer escuridão para os belos e um dos primeiros, de seu tipo, sistemas. Observo apenas que na empresa em que esse sistema foi introduzido, o pessoal não treinado não sabia como usá-lo e, portanto, ao mudar as pessoas em cargos no departamento de trabalho e salários, ninguém conseguia adaptar completamente o sistema às mudanças de condições. Então, eles o mantiveram como um grande artefato antigo, que ninguém sabia ler, exceto os Velhos Crentes, e eles não foram mais deixados.

Faça alterações

(desenvolvimento do modelo)
Normalmente, para a implementação de modelos multifatoriais, necessários para obter um único resultado numérico, prefiro o método de avaliação complexa com base em árvores de critérios, matrizes de convolução e um sistema para reduzir critérios para uma única escala.

Em resumo, as vantagens de tais construções são as possibilidades:

• aplicação de um número ilimitado de fatores de avaliação;
• realização da não linearidade e variabilidade do grau de influência dos fatores;
• inclusão de fatores de vários tipos (com alterações físicas, estimativas de especialistas, tabelas de correspondência etc.);
• prever resultados e esperar valores em um determinado intervalo.

A facilidade de uso de tais mecanismos é combinada com sucesso com a multivariância da estimativa resultante, pois mesmo em um intervalo numérico limitado de 1-4, que exige uma avaliação abrangente, é possível obter uma variedade suficiente.


Figura 2. O diagrama de blocos do recebimento das notas e sua transferência para os salários dos funcionários.
A idéia era que, de acordo com vários critérios, fosse feita uma avaliação da “significância” para os negócios da unidade estrutural e da posição específica para essa unidade.

Em geral, de acordo com esse esquema, é necessário observar:

• para cada unidade, seu próprio cálculo é formado de acordo com um único modelo de avaliação integrado;
• no modelo de avaliação integrada, fatores quantitativamente mensuráveis ​​e especialistas podem ser usados;
• após a obtenção de todos os valores do modelo para cada departamento e cada posição, é realizada a multiplicação da matriz, onde o resultado geral é formado;
• para levar notas ao tamanho dos salários, é aplicado um modelo para levar notas aos salários dos funcionários do departamento.

Na formação da avaliação de significância do departamento, foram utilizados os seguintes critérios:

1. De acordo com o nível de processos: principal, auxiliar, serviço;
2. Pelo grau de universalidade das tarefas que estão sendo resolvidas: universal, específica, situacional;
3. Pelo nível de interação: entre organizações; entre unidades organizacionais; interação interna.

Nos critérios de avaliação apresentados, sempre existem três opções para cada critério. Essas opções são organizadas “em ordem decrescente” com significância da classificação 4 à classificação 1. A opção média corresponde a uma classificação de 2,5. Aplicando essa redução, todas as estimativas podem ser traduzidas na escala de avaliação complexa padrão 1-4 (aqui você só precisa aceitar ... concordamos).
O tipo básico da árvore para avaliar a significância da posição foi formado da seguinte forma:

1. Nível de posição: gerentes, especialistas, artistas;
2. Tipos de tarefas: organizacional, criativa, regulamentada;
3. Conectividade de tarefas: com o ambiente externo, entre unidades, dentro de unidades.

Um exemplo disso é o modelo de avaliação integrada, que, a propósito, conseguimos "direcionar" para o Excel, ou seja, disponibilizar, mostra como é fácil realizar um procedimento de avaliação.


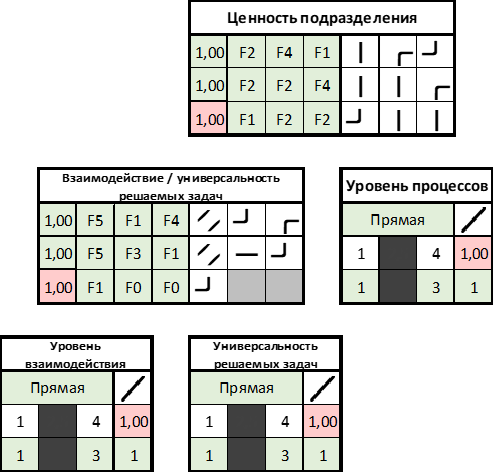Figura 3. Vista geral do modelo de avaliação integrado “Unit Value”.
Após compilar um modelo, cada critério para cada unidade (e para postos, respectivamente, tem seu próprio modelo) recebe sua própria classificação, e o sistema simplesmente o considera. Resta escrever esses valores.

Como é o "resumo" das notas no final?


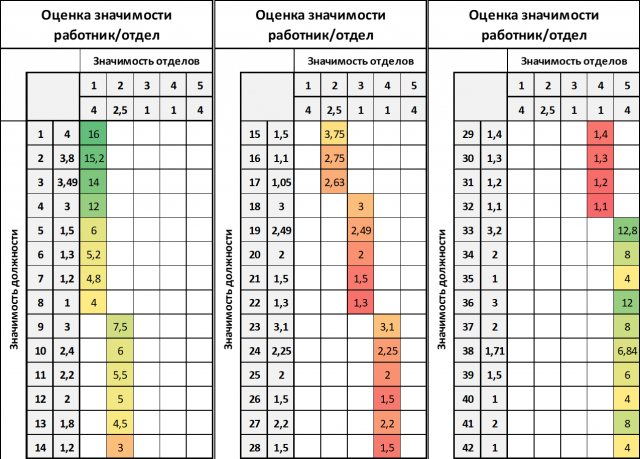Figura 4. Um exemplo de cálculo de uma nota do tipo “significância do departamento / significância da posição”.

Nesse caso, o ideal parecia ser a multiplicação de "significância de departamento" e "significância de posição". O resultado foi bastante diferenciado e pode ser utilizado para determinar a escala tarifária.

Último componente

Como você se lembra, de acordo com a Figura 2, agora é necessário converter a classificação da bola em salário.

Supunha-se originalmente que isso pudesse ser feito usando uma função linear simples. Para esses propósitos, o tomador de decisão (o tomador de decisão) é convidado a simplesmente indicar o salário mínimo e máximo na empresa. Um movimento bastante simples e lógico, como parecia.

A primeira e óbvia tentativa é encaixar com um circuito linear. Com os parâmetros indicados, o tomador de decisão (o chefe de uma das Universidades) obteve tal resultado que o chefe da unidade estrutural, tendo recebido nota 13, deveria receber um salário superior a 200 mil (chefe do departamento).


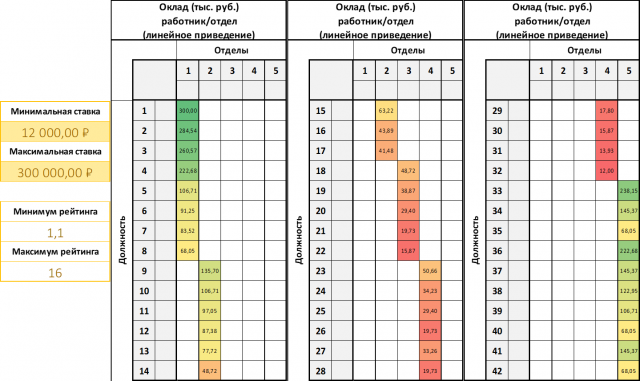Figura 5. Um exemplo de “exposição” de notas a salários usando uma escala de elenco linear.

A necessidade de implementar um sistema simples para a formação de redução não linear de salários / notas tornou-se aparente. Nesse caso, foi necessário simplificar o processo de "seleção" da redução ideal o máximo possível.

As curvas de Bezier vieram à mente por acidente. Como os pontos extremos da curva são determinados automaticamente (notas mínimas e máximas / salários mínimos e máximos), o tomador de decisão precisará mudar um / dois pontos para obter o tipo de curva desejado.


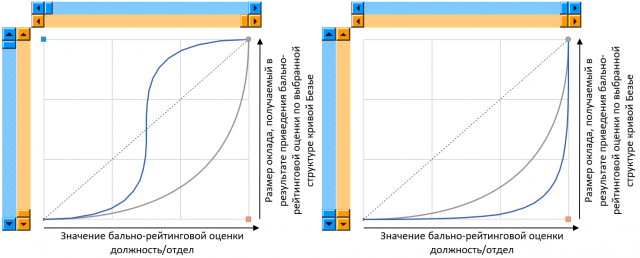Figura 6. O controle gráfico da curva de Bezier implementado no Excel
Inicialmente, foi feita uma tentativa de contornar apenas uma versão quadrática da curva; no entanto, depois de tentar construir, ficou claro que eles não podiam contornar e era necessário implementar uma versão cúbica da função.

Para gerar uma curva de Bezier no Excel, são necessárias as seguintes ações:

• Designe os pontos extremos no gráfico pelas coordenadas X, Y: (1; 1) e (4; 4) - neste exemplo. Essas coordenadas extremas são tomadas para tornar o gráfico claro. Ele não é obrigado a mostrar uma conexão real, mas apenas a mostrar dependência;
• Designe coordenadas para os pontos deslocados pelo LPR: um ponto para uma curva quadrática e dois pontos para um cúbico;
• Defina a etapa de cálculo para a curva (no nosso exemplo - 0,5) e calcule os pares de pontos para a curva.

Após a construção das curvas, o tomador de decisão recebeu uma ferramenta de controle visual. No entanto, para aplicar as curvas, é necessário implementar o processo de obtenção da coordenada Y a partir da coordenada Y indicada. Aqui estava o maior problema em si. No entanto, foi possível implementar o código VBA que permite executar essas operações.

Para uma função quadrática:

Function __Y__X__( _ X As Double, _ X1 As Double, _ X2 As Double, _ X3 As Double, _ Y1 As Double, _ Y2 As Double, _ Y3 As Double) As Double Dim aX, bX, cX, aY, bY, cY, Temp, dis, X_1, X_2, X_f, Y_f As Double aX = X1 - 2 * X2 + X3 bX = -2 * X1 + 2 * X2 cX = X1 - X aY = Y1 - 2 * Y2 + Y3 bY = -2 * Y1 + 2 * Y2 cY = Y1 dis = bX * bX - 4 * aX * cX If aX <> 0 Then X_1 = (-bX + (dis ^ (1 / 2))) / (2 * aX) X_2 = (-bX - (dis ^ (1 / 2))) / (2 * aX) Else X_1 = -cX / bX End If If Not IsEmpty(X_1) Then If ((CDbl(CStr(X_1)) >= 0) And (CDbl(CStr(X_1)) <= 1)) Then X_f = X_1 If Not IsEmpty(X_2) Then If ((CDbl(CStr(X_2)) >= 0) And (CDbl(CStr(X_2)) <= 1)) Then X_f = X_2 Y_f = ((1 - X_f) ^ 2) * Y1 + 2 * (1 - X_f) * X_f * Y2 + (X_f ^ 2) * Y3 '=(1-R[-1]C[-1];2)*R58C2+2*(1-R[-1]C[-1])*R[-1]C[-1]*R58C3+(R[-1]C[-1];2)*R58C5 a = a __Y__X__ = Y_f End Function 

Para função cúbica:

 Function __Y__X__( _ X As Double, _ X1 As Double, _ X2 As Double, _ X3 As Double, _ X4 As Double, _ Y1 As Double, _ Y2 As Double, _ Y3 As Double, _ Y4 As Double) As Double Dim myPi, aX, bX, cX, dX, aY, bY, cY, dY, Q, P, S, Temp, fi, dis, X_1, X_2, X_3, X_f, Y_f As Double 'Exit Function 'If X1 = 1.5 Or X = 0 Or X1 = 0 Or X2 = 0 Or X3 = 0 Or X4 = 0 Then Exit Function 'Application.Volatile True myPi = WorksheetFunction.Acos(-1) aX = -X1 + (3 * X2) - (3 * X3) + X4 bX = 3 * X1 - 6 * X2 + 3 * X3 cX = -3 * X1 + 3 * X2 dX = X1 - X aY = -Y1 + 3 * Y2 - 3 * Y3 + Y4 bY = 3 * Y1 - 6 * Y2 + 3 * Y3 cY = -3 * Y1 + 3 * Y2 dY = Y1 If aX < 0.000001 And aX > -0.000001 Then _ aX = 0 If CDbl(CStr(aX)) <> 0 Then Temp = aX aX = aX / Temp bX = bX / Temp cX = cX / Temp dX = dX / Temp Q = (bX ^ 2 - 3 * cX) / 9 P = (2 * (bX ^ 3) - 9 * bX * cX + 27 * dX) / 54 S = Q ^ 3 - P ^ 2 'X1 = -1 'X2 = -1 'X3 = -1 T = T If S < 0.00000001 And S > -0.00000001 Then _ S = 0 If P < 0.00000001 And P > -0.00000001 Then _ P = 0 If Q < 0.00000001 And Q > -0.000000001 Then _ Q = 0 If S > 0 Then fi = (1 / 3) * WorksheetFunction.Acos(P / ((Q ^ 3) ^ (1 / 2))) X_1 = -2 * (Q ^ (1 / 2)) * Cos(fi) - bX / 3 X_2 = -2 * (Q ^ (1 / 2)) * Cos(fi + 2 * myPi / 3) - bX / 3 X_3 = -2 * (Q ^ (1 / 2)) * Cos(fi - 2 * myPi / 3) - bX / 3 ElseIf S = 0 Then fi = 0 X_1 = -2 * (P ^ (1 / 3)) - bX / 3 X_2 = (P ^ (1 / 3)) - bX / 3 Else If Q > 0 Then fi = (1 / 3) * WorksheetFunction.Acosh(Abs(P) / ((Q ^ 3) ^ (1 / 2))) X_1 = -2 * Sgn(P) * (Q ^ (1 / 2)) * WorksheetFunction.Cosh(fi) - bX / 3 ElseIf Q = 0 Then fi = 0 T = (dX - (bX ^ 3) / 27) X_1 = -((Abs(T) ^ (1 / 3)) * (2 * (T < 0) + 1)) - bX / 3 'T = (dX - (bX ^ 3) / 27) 'T = (Abs(T) ^ (1 / 3)) * ((T < 0) + 1) 'X_1 = -T - bX / 3 Else fi = (1 / 3) * WorksheetFunction.Asinh(Abs(P) / ((Abs(Q) ^ 3) ^ (1 / 2))) X_1 = -2 * Sgn(P) * (Abs(Q) ^ (1 / 2)) * WorksheetFunction.Sinh(fi) - bX / 3 End If End If If Not IsEmpty(X_1) Then If ((CDbl(CStr(X_1)) >= 0) And (CDbl(CStr(X_1)) <= 1)) Then X_f = X_1 If Not IsEmpty(X_2) Then If ((CDbl(CStr(X_2)) >= 0) And (CDbl(CStr(X_2)) <= 1)) Then X_f = X_2 If Not IsEmpty(X_3) Then If ((CDbl(CStr(X_3)) >= 0) And (CDbl(CStr(X_3)) <= 1)) Then X_f = X_3 a = a Else dis = cX * cX - 4 * bX * dX If bX < 0.000001 And bX > -0.000001 Then _ bX = 0 If bX <> 0 Then X_1 = (-cX + (dis ^ (1 / 2))) / (2 * bX) X_2 = (-cX - (dis ^ (1 / 2))) / (2 * bX) Else X_1 = -dX / cX End If If Not IsEmpty(X_1) Then If ((CDbl(CStr(X_1)) >= 0) And (CDbl(CStr(X_1)) <= 1)) Then X_f = X_1 If Not IsEmpty(X_2) Then If ((CDbl(CStr(X_2)) >= 0) And (CDbl(CStr(X_2)) <= 1)) Then X_f = X_2 End If a = a Y_f = ((1 - X_f) ^ 3) * Y1 + 3 * ((1 - X_f) ^ 2) * X_f * Y2 + 3 * (1 - X_f) * (X_f ^ 2) * Y3 + (X_f ^ 3) * Y4 'Debug.Print (Y_f) __Y__X__ = Y_f End Function 

No processo, foram feitas tentativas para encontrar uma opção pronta na rede e reciclar, mas isso não aconteceu. Também foi descoberto acidentalmente que o VBA não é capaz de extrair corretamente uma raiz de grau ímpar de um número negativo. Somente uma certa combinação permitiu corrigir a situação:

 T = (dX - (bX ^ 3) / 27) X_1 = -((Abs(T) ^ (1 / 3)) * (2 * (T < 0) + 1)) - bX / 3 

* -possivelmente no código, permanece em outro lugar um momento associado a esse cálculo. Um bug foi descoberto durante a redação do artigo)

Construções resultantes

Portanto, compare os resultados (construídos de acordo com o tipo de curvas na Figura 6 (gráfico à direita)):


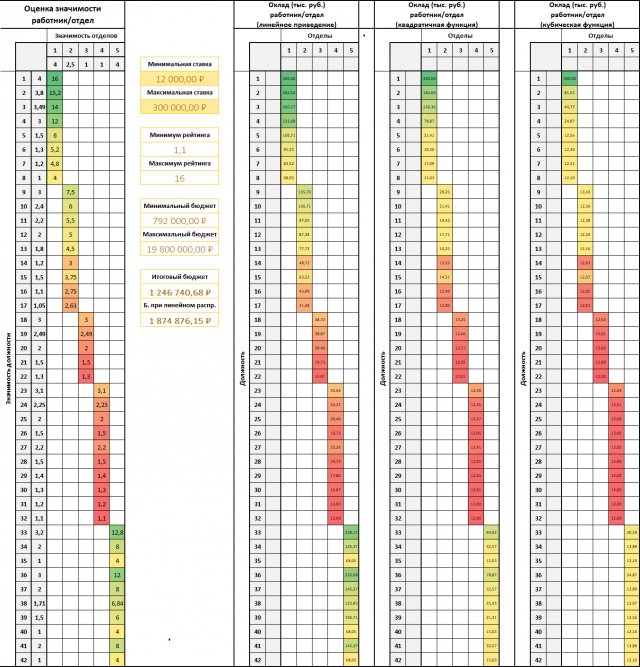Figura 7. Comparação de modelos de notas com salários reais (reflexo da flexibilidade do sistema)

Pode ser visto na figura que a função cúbica permite ainda mais "dobrar" a dependência da classificação da bola e do salário real (o gerente, infelizmente, ficou satisfeito com esta opção).

De qualquer forma, esse trabalho, embora seja puramente experimental, não foi realmente lançado em nenhum lugar, mas, como parece aos autores, pode ser útil em desenvolvimentos do mundo real.

Espero que ela não "deite na prateleira", mas alguém será necessário.