Splines em gráficos 3D, a opção mais automatizada

Há cerca de um mês, comecei a aprender Python com o livro Dawson e acordei profundamente no processo de escrever meu jogo no pygame. TK era tal que parecia mais promissor fazer um jogo com gráficos pseudo-tridimensionais, colocando as superfícies salvas dos splines 3D em sprites. Vou escrever sobre o último.

Portanto, existem polígonos (é mais fácil trabalhar com quadrângulos) nos quais queremos esticar superfícies cúbicas para que elas se encaixem perfeitamente - essas superfícies são estrias.



É mais conveniente apresentar um spline para um polígono como uma função

$$

$$g (u, v) = v \ cdot g_1 (u) + (1 - v) \ cdot g_2 (u) + u \ cdot g_3 (v) + (1-u) \ cdot g_4 (v) (1)$$

Aqui

$$

$$g_1, g_2, g_3, g_4$$

- polinômios cúbicos que satisfazem algumas condições de contorno (na figura abaixo - curvas verde claro e vermelho e condições derivadas-iniciais - vetores lilás e azul); uev variam de 0 a 1.



Nesta interpretação, alguns graus são perdidos (produtos de 2 e 3 graus de parâmetros), mas os coeficientes polinomiais podem ser encontrados especificando apenas 12 vetores de condições iniciais (4 pontos poligonais e vetores derivativos em relação a u e v para cada ponto). Nas junções, splines coincidem se condições iniciais semelhantes forem definidas para polígonos vizinhos (os vetores derivativos devem ser colineares, a superfície passa pelos mesmos pontos do polígono).

Um problema - a derivada com essa afirmação do problema em toda a borda pode não coincidir - haverá pequenos artefatos nas junções. Você pode pensar em mais 4 condições para corrigir isso e adicionar cuidadosamente outro termo à fórmula

$$

$$u \ cdot v \ cdot (u-1) \ cdot (v-1) \ cdot g_5 (u, v)$$

que não estraga as fronteiras, mas esse é um tópico para um artigo separado.

Uma alternativa é a superfície de Bezier , mas propõe definir 16 parâmetros de significado matemático incompreensível (para mim), ou seja, supõe-se que o artista trabalhe com suas próprias mãos. Isso não é muito adequado para mim, então uma bicicleta com muletas segue.

Os coeficientes (1) são mais facilmente calculados encontrando a matriz inversa à matriz de valores e derivadas nos cantos e multiplicando pelas condições de entrada (três vezes, para cada coordenada). A matriz pode ser esta:


O NumPy faz um excelente trabalho nisso.

Uma questão permanece - onde obter os vetores dos derivativos. Supõe-se que eles devam ser selecionados de alguma forma com base na posição dos pontos vizinhos (para o polígono) e por motivos de suavidade.
Para mim, pessoalmente, ainda era completamente contra-intuitivo como lidar com o comprimento do vetor derivado. A direção é compreensível, mas o comprimento?

Como resultado, nasceu o seguinte algoritmo:

1. Na primeira etapa, ocorre uma classificação de pontos. No gráfico (que pontos dos polígonos e suas conexões especificam), os ciclos de comprimento 4 são pesquisados ​​e armazenados e, além disso, são registrados os vizinhos mais adequados para a função de estender as arestas do polígono (é determinado antecipadamente quais arestas correspondem a uma alteração no parâmetro u e qual corresponde a v). Aqui está um pedaço de código que pesquisa, classifica e lembra os vizinhos pelo 0º ponto de um ciclo:


Além disso, ao construir o spline, a derivada ao longo da aresta (por exemplo, com relação ao parâmetro u) no ponto do polígono é selecionada com base na localização de dois pontos da aresta e um ponto adjacente (sejam os pontos vec1, vec2 e vec3; o ponto no qual a derivada é procurada é o segundo).



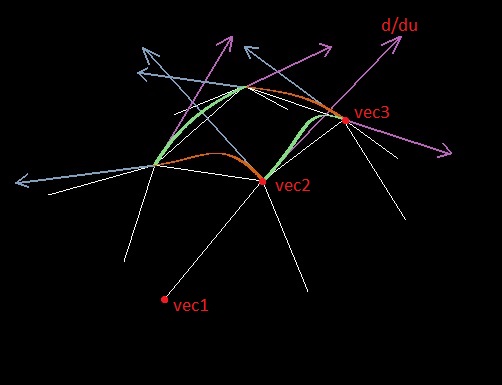
Inicialmente, tentei usar o vetor normalizado vec3 - vec1 (como apliquei o teorema de Lagrange) para esse papel, mas surgiram problemas precisamente com o comprimento do vetor derivado - tornar uma constante uma má ideia.

Digressão lírica:

Para uma pequena ilustração do que o vetor derivado é na versão paramétrica, passamos a uma analogia bidimensional simples - aqui está uma parte de um arco circular:

$$

$$g (u) = (Rsin (u \ pi / 2), Rcos (u \ pi / 2))$$

$$

$$g '(u) = (R \ pi / 2 \ cdot cos (u \ pi / 2), -R \ pi / 2 \ cdot sin (u \ pi / 2))$$

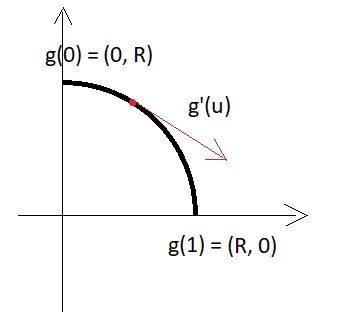
I.e. módulo derivativo = R * pi / 2 e, de um modo geral, depende do tamanho da peça do arco, que definimos através do parâmetro

O que fazer com isso agora? Leo Tolstoi nos disse que tudo é redondo = bom; portanto, se definirmos a derivada em um ponto como se desejássemos construir um arco lá, obteremos uma curva suave e bonita.

O fim da digressão.

A segunda etapa da pesquisa derivada:

2. Através de nossos três pontos vec1, vec2, vec3, construímos um plano; nesse plano, procuramos um círculo que passa por todos os três pontos. A derivada desejada será direcionada ao longo da tangente ao círculo no ponto vec2, e o módulo do vetor da derivada deve ser igual ao produto do raio do círculo e do ângulo do setor, que formam dois pontos da face do polígono (semelhante à nossa analogia simples e plana a partir da digressão lírica).

$$

$$g '= R \ cdot \ phi$$

Tudo parece simples, eis o código da função, por exemplo (o NumPy é usado novamente):


Bem, em geral, tudo funciona de alguma forma. Para demonstração, peguei um cubo 5x5x5 e alterei a posição dos pontos com um randomizador: