Por que precisamos de intervalos de C ++ 20 em um triturador simples?

Recentemente, os intervalos que devem ser incluídos no padrão C ++ 20 foram discutidos bastante, inclusive no Habré ( um exemplo em que existem muitos exemplos ). Existem críticos suficientes de intervalos, eles dizem que

• eles são muito abstratos e são necessários apenas para códigos muito abstratos
• a legibilidade do código com eles só piora
• intervalos abrandar código

Vamos ver completamente camponês tarefa prática, a fim de entender se essa crítica é válida e é verdade que Eric Nibler foi mordido por Bartosz Milewski e escreve range-v3 apenas com a lua cheia .

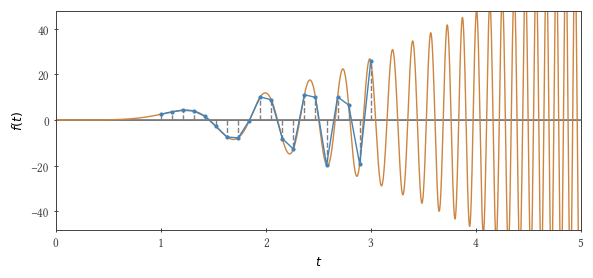
Integraremos a seguinte função usando o método trapézio:$$ $ inline $ f (t) = 3 t ^ 2 \ sin t ^ 3 $ inline $ variando de zero a$$ $ inline $ \ tau $ inline $ . Se$$ $ inline $ \ tau ^ 3 / \ pi $ inline $ é igual a um número ímpar, então a integral é 2.

Então, o problema: escrevemos um protótipo de uma função que calcula a integral pelo método trapezoidal . Parece, à primeira vista, que abstrações não são necessárias aqui, mas a velocidade é importante. De fato, isso não é inteiramente verdade. Para o trabalho, muitas vezes tenho que escrever "esmagadores de números", o principal usuário dos quais sou eu. Então, eu também tenho que apoiar e lidar com os erros deles (infelizmente meus colegas - nem sempre só eu). E também acontece que algum código não é usado, digamos, um ano e depois ... Em geral, documentação e testes também precisam ser escritos.

Quais argumentos uma função integradora deve ter? Função e grade integráveis ​​(conjunto de pontos$$ $ inline $ t_1, t_2, t_3 ... $ inline $ usado para calcular a integral). E se tudo estiver claro com a função integrada (a função std::function estará aqui), de que forma a grade deve ser transmitida? Vamos ver

Opções

Para começar - para que haja algo com o qual comparar o desempenho -, escreveremos um loop for simples com uma etapa de tempo constante:

 // trapezoidal rule of integration with fixed time step; // dt_fixed is the timestep; n_fixed is the number of steps double integrate() { double acc = 0; for(long long i = 1; i < n_fixed - 1; ++i) { double t = dt_fixed * static_cast<double>(i); acc += dt_fixed * f(t); } acc += 0.5 * dt_fixed * f(0); acc += 0.5 * dt_fixed * f(tau); return acc; } 

Ao usar esse ciclo, você pode passar como argumentos para a função o início e o fim do intervalo de integração, bem como o número de pontos para essa integração em si. Parar - o método trapézio também acontece com uma etapa variável, e nossa função integrável simplesmente pede para usar uma etapa variável! Então, vamos ter mais um parâmetro ($$ $ inline $ b $ inline $ ) para controlar a "não linearidade" e permitir que nossos passos sejam, por exemplo, os seguintes:$$ $ inline $ \ Delta t (t) = \ Delta t_0 + bt $ inline $ . Essa abordagem (introduzir um parâmetro numérico adicional) provavelmente é usada em um milhão de lugares, embora, ao que parece, sua falha deva ser óbvia para todos. E se tivermos uma função diferente? E se precisarmos de um pequeno passo em algum lugar no meio do nosso intervalo numérico? Mas e se uma função integrável tiver alguns recursos? Em geral, devemos ser capazes de transmitir qualquer grade. (No entanto, nos exemplos, até o final, “esqueceremos” o método trapezoidal real e, por simplicidade, consideraremos sua versão com um passo constante, tendo em mente que a grade pode ser arbitrária).

Como a grade pode ser qualquer, vamos passar seus valores$$ $ inline $ t_1, t_2, ... $ inline $ embrulhado em std::vector .

 // trapezoidal rule of integration with fixed time step double integrate(vector<double> t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } 

Existem comunidades mais do que suficientes nessa abordagem, mas e o desempenho? Com consumo de memória? Se anteriormente tudo foi resumido no processador, agora precisamos primeiro preencher a área de memória e depois ler a partir dela. E a comunicação com a memória é uma coisa bastante lenta. E a memória ainda não é de borracha ( e silicone )

Vamos olhar para a raiz do problema. O que uma pessoa precisa para ser feliz? Mais precisamente, do que o nosso ciclo (baseado em intervalo para loop) precisa? Qualquer contêiner com iteradores begin() e end() e ++ , * e != Operadores para iteradores. Então vamos escrever.

 //   ,    ,      template <typename T> double integrate(T t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } // ... //      class lazy_container { public: long long int n_nodes; lazy_container() { n_nodes = n_fixed; } ~lazy_container() {} class iterator { public: long long int i; // index of the current node iterator() { i = 0; } ~iterator() {} iterator& operator++() { i+= 1; return *this; } // ! bool operator!=(const iterator& rhs) const { return i != rhs.i; } double operator* () const { return dt_fixed * static_cast<double>(i); } }; iterator begin() { return iterator(); } iterator end() { iterator it; it.i = n_nodes; return it; } }; // ... //      lazy_container t_nodes; double res = integrate(t_nodes); 

Estamos calculando um novo valor aqui.$$ $ inline $ t_i $ inline $ sob demanda, assim como fizemos em um loop for simples. Não há acesso à memória e espera-se que os compiladores modernos simplifiquem o código com muita eficiência. Ao mesmo tempo, o código da função de integração não mudou muito e ainda pode digerir std::vector .

Onde está a flexibilidade? De fato, agora podemos escrever qualquer função no operador ++ . Ou seja, essa abordagem permite, de fato, transferir uma função em vez de um único parâmetro numérico. A grade gerada em tempo real pode ser qualquer, e nós (provavelmente) também não perdemos o desempenho. No entanto, escrever um novo lazy_container todas as vezes, para distorcer a grade de uma maneira diferente, não parece nada disso (são as mesmas 27 linhas!). Obviamente, você pode tornar a função responsável por gerar a grade um parâmetro de nossa função de integração e lazy_container também, isto é, com licença, encapsular.

Você pergunta - então algo estará errado de novo? Sim Primeiramente, será necessário transmitir separadamente o número de pontos para integração, o que pode causar um erro. Em segundo lugar, a bicicleta não padronizada criada precisará ser suportada e possivelmente desenvolvida por alguém. Por exemplo, você pode imaginar imediatamente como, com essa abordagem, compor um combinador para funções no operador ++ ?

C ++ há mais de 30 anos. Muitos nessa idade já têm filhos e o C ++ nem sequer possui contêineres / iteradores preguiçosos padrão. Um pesadelo! Mas tudo (no sentido de iteradores, não de crianças) mudará já no próximo ano - o padrão (possivelmente parcialmente) incluirá a biblioteca range-v3 , desenvolvida por Eric Nibler por vários anos. Usaremos as obras de seus frutos. O código diz tudo por si:

 #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... auto t_nodes = ranges::v3::iota_view(0, n_fixed) | ranges::v3::views::transform( [](long long i){ return dt_fixed * static_cast<double>(i); } ); double res = integrate(t_nodes); 

A função de integração permanece a mesma. Ou seja, apenas 3 linhas para resolver o nosso problema! Aqui iota_view(0, n) gera um intervalo lento (intervalo, um objeto que encapsula o início e o fim generalizados; um intervalo lento é uma visualização), que, ao iterar a cada etapa, calcula o próximo número no intervalo [0, n). É engraçado que o nome ι (a letra grega iota) se refira há 50 anos à língua da APL. Vara | permite escrever pipelines de modificadores de intervalo e transform , de fato, um modificador que, usando uma função lambda simples, transforma uma sequência de números inteiros em uma série$$ $ inline $ t_1, t_2, ... $ inline $ . Tudo é simples, como em um conto de fadas Haskell.

Mas como dar um passo variável? Tudo é tão simples:

 #include <range/v3/view/drop.hpp> #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... // trapezoidal rule of integration; step size is not fixed template <typename T> double integrate(T t_nodes) { double acc = 0; double t_prev = *(t_nodes.begin()); double f_prev = f(t_prev); for (auto t: t_nodes | ranges::v3::views::drop(1)) { double f_curr = f(t); acc += 0.5 * (t - t_prev) * (f_curr + f_prev); t_prev = t; f_prev = f_curr; } return acc; } //... auto step_f = [](long long i) { if (static_cast<double>(i) <= 1 / a) { return pow(2 * M_PI, 1/3.0) * a * static_cast<double>(i); } else { return tau * pow(static_cast<double>(i) / static_cast<double>(n), 1/3.0); } }; auto t_nodes = ranges::v3::iota_view(0, n) | ranges::v3::views::transform(step_f); double res = integrate(t_nodes); 

Um leitor atento observou que, em nosso exemplo, a etapa variável nos permitiu reduzir o número de pontos da grade em um fator de três, enquanto, além disso, há despesas visíveis na computação$$ $ inline $ t_i $ inline $ . Mas se dermos outra$$ $ inline $ f (t) $ inline $ , o número de pontos pode mudar muito mais ... (mas aqui o autor já está se tornando preguiçoso).

Então os horários

Temos as seguintes opções:

• v1 - loop simples
• v2 -$$ $ inline $ t_i $ inline $ mentir em std::vector
• v3 - lazy_container improvisado com iterador improvisado
• v4 - intervalos de C ++ 20 (intervalos)
• v5 - varia novamente, mas somente aqui o método trapézio é escrito usando um tom variável

Aqui está o que acontece (em segundos) para$$ $ inline $ \ tau = (10 \, 000 \, 001 \ times \ pi) ^ {1/3} $ inline $ , para g ++ 8.3.0 e clang ++ 8.0.0 na Intel® Xeon® CPU® X5550 (número de etapas sobre$$ $ inline $ 1,5 \ vezes 10 ^ 8 $ inline $ , exceto na v5, em que as etapas são três vezes menores (o resultado dos cálculos de todos os métodos difere dos dois em não mais que 0,07):

Em geral, a mosca atravessou o campo, a mosca encontrou uma moeda!

Sumário

Mesmo em uma tarefa muito simples, os intervalos se mostraram muito úteis: em vez de código com iteradores criados em mais de 20 linhas, escrevemos 3 linhas, sem problemas com a legibilidade do código ou seu desempenho.

Obviamente, se precisássemos (para) do desempenho final desses testes, teríamos que tirar o máximo proveito do processador e da memória escrevendo código paralelo (ou escrevendo uma versão no OpenCL) ... Além disso, não tenho idéia do que acontecerá se escrever cadeias muito longas de modificadores. É fácil depurar e ler mensagens do compilador ao usar intervalos em projetos complexos. O tempo de compilação aumentará. Espero que alguém escreva sobre este artigo.

Quando escrevi esses testes, eu mesmo não sabia o que iria acontecer. Agora eu sei - os intervalos definitivamente merecem ser testados em um projeto real, nas condições em que você pretende usá-los.

Fui ao bazar comprar um samovar.

Links úteis

range-v3 em casa

Documentação e estudos de caso v3

código deste artigo no github

listas em haskell, para comparação

Agradecimentos

Obrigado fadey por ajudar a escrever tudo isso!

PS

Espero que alguém comente essas esquisitices: i) Se você tomar o intervalo de integração 10 vezes menor, no meu Xeon o exemplo v2 é 10% mais rápido que o v1 e v4 é três vezes mais rápido que o v1. ii) O compilador Intel (icc 2019) às vezes nesses exemplos cria código duas vezes mais rápido que o compilado g ++. A vetorização é a culpada? O g ++ pode ser forçado a fazer o mesmo?