Introdução às dependências funcionais

Neste artigo, falaremos sobre dependências funcionais em bancos de dados - o que é, onde é aplicado e quais algoritmos existem para sua pesquisa.

Consideraremos dependências funcionais no contexto de bancos de dados relacionais. Falando de maneira muito rude, em tais bancos de dados as informações são armazenadas na forma de tabelas. Além disso, usamos conceitos aproximados, que em uma teoria relacional estrita não são intercambiáveis: chamaremos a própria tabela de relação, colunas - atributos (seu conjunto - um diagrama de relacionamento) e um conjunto de valores de linha em um subconjunto de atributos - uma tupla.



Por exemplo, na tabela acima, (órgão de Benson, M, M ) é uma tupla de atributos (Paciente, Gênero, Médico) .
Mais formalmente, isso está escrito da seguinte maneira: $$$t_ {1}$ [ Paciente, Paul, Médico ] = (Benson, M, M órgão) .
Agora podemos introduzir o conceito de dependência funcional (FZ):

Definição 1. A relação R satisfaz a lei federal X → Y (onde X, Y ⊆ R) se e somente se para quaisquer tuplas $$$t_ {1}$ , $$$t_ {2}$ Holds R mantém: se $$$t_ {1}$ [X] = $$$t_ {2}$ [X] então $$$t_ {1}$ [Y] = $$$t_ {2}$ [Y] Nesse caso, diz-se que X (um conjunto determinante ou definidor de atributos) define funcionalmente Y (um conjunto dependente).

Em outras palavras, a presença da Lei Federal X → Y significa que se tivermos duas tuplas em R e elas coincidirem nos atributos de X , elas também coincidirão nos atributos de Y.
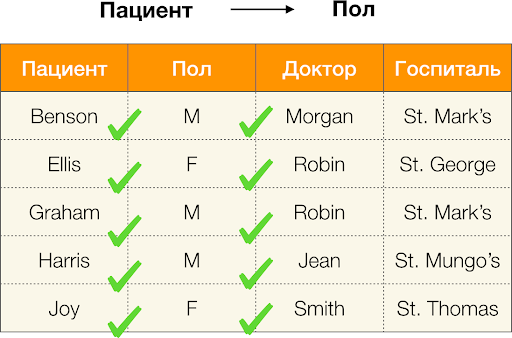
E agora em ordem. Considere os atributos Paciente e Gênero para os quais queremos descobrir se existem dependências entre eles ou não. Para tantos atributos, as seguintes dependências podem existir:

1. Paciente → Sexo
2. Sexo → Paciente

De acordo com a definição acima, para manter a primeira dependência, apenas um valor da coluna Sexo deve corresponder a cada valor exclusivo da coluna Paciente . E para a tabela de amostra, isso é verdade. No entanto, isso não funciona na direção oposta, ou seja, a segunda dependência não é cumprida e o atributo Paul não é determinante para o Paciente . Da mesma forma, se você usar a dependência Médico → Paciente , poderá ver que ela é violada, pois o valor Robin para esse atributo tem vários valores diferentes - Ellis e Graham .

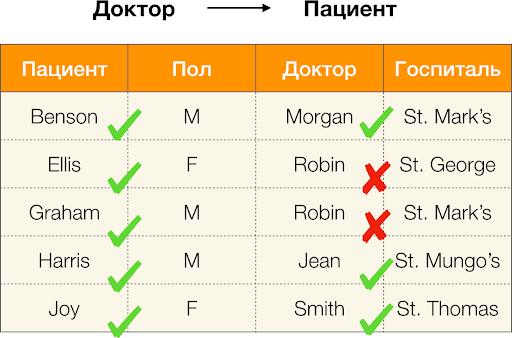
Assim, dependências funcionais tornam possível determinar os relacionamentos existentes entre os conjuntos de atributos da tabela. A partir de agora, consideraremos os relacionamentos mais interessantes, ou melhor, X → Y, de modo que sejam:

• não trivial, isto é, o lado direito da dependência não é um subconjunto da esquerda (Y ̸⊆ X) ;
• mínimo, isto é, não existe tal dependência Z → Y tal que Z ⊂ X.

As dependências consideradas até o momento eram rigorosas, ou seja, não incluíam violações na tabela, mas além delas existem também aquelas que permitem alguma inconsistência entre os valores das tuplas. Tais dependências são colocadas em uma classe separada, chamada aproximada, e podem ser violadas em um determinado número de tuplas. Este valor é regulado pelo indicador de erro máximo emax. Por exemplo, a proporção de erro $$$e_ {max}$ = 0,01 pode significar que a dependência pode ser violada por 1% das tuplas disponíveis no conjunto de atributos considerado. Ou seja, para 1000 registros, no máximo 10 tuplas podem violar a Lei Federal. Consideraremos uma métrica ligeiramente diferente com base em valores diferentes em pares das tuplas comparadas. Para a dependência X → Y da relação r, é considerado o seguinte:

$$

$$e (X \ rightarrow Y, r) = \ frac {| \ {(t_1, t_2) \ em r ^ 2 \ | \ t_1 [X] = t_2 [X] \ cunha t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ 2 | - | r |}$$

Calculamos o erro para Médico → Paciente a partir do exemplo acima. Temos duas tuplas, cujos valores diferem no atributo Paciente , mas coincidem no Médico : $$$t_ {1}$ [ Doutor, Paciente ] = ( Robin, Ellis ) e $$$t_ {2}$ [ Médico, Paciente ] = ( Robin, Graham ). Seguindo a definição de erro, devemos levar em consideração todos os pares conflitantes, o que significa que haverá dois deles: ( $$$t_ {1}$ , $$$t_ {2}$ ) e sua inversão ( $$$t_ {2}$ , $$$t_ {1}$ ) Substitua na fórmula e obtenha:

$$

$$\ frac {2} {5 ^ 2 - 5} = 0,1$$

Agora vamos tentar responder à pergunta: "Por que tudo isso?". De fato, as leis federais são diferentes. O primeiro tipo são dependências determinadas pelo administrador no estágio de design do banco de dados. Geralmente são poucos, são rigorosos e a principal aplicação é a normalização de dados e o design do esquema de relacionamento.

O segundo tipo são dependências que representam dados "ocultos" e relacionamentos anteriormente desconhecidos entre atributos. Ou seja, essas dependências não foram pensadas no momento do design e já são encontradas para o conjunto de dados existente, para que, com base no conjunto de leis federais identificadas, tire conclusões sobre as informações armazenadas. É com essas dependências que estamos trabalhando. Eles estão envolvidos em uma área inteira de mineração de dados com várias técnicas de pesquisa e algoritmos construídos com base em suas informações. Vamos entender como as dependências funcionais encontradas (exatas ou aproximadas) em qualquer dado podem ser úteis.



Hoje, a limpeza de dados está entre as principais áreas de uso de dependência. Envolve o desenvolvimento de processos para identificar "dados sujos" com sua posterior correção. Representantes brilhantes de "dados sujos" são duplicatas, erros ou erros de digitação, valores ausentes, dados desatualizados, espaços extras e similares.

Exemplo de erro de dados:



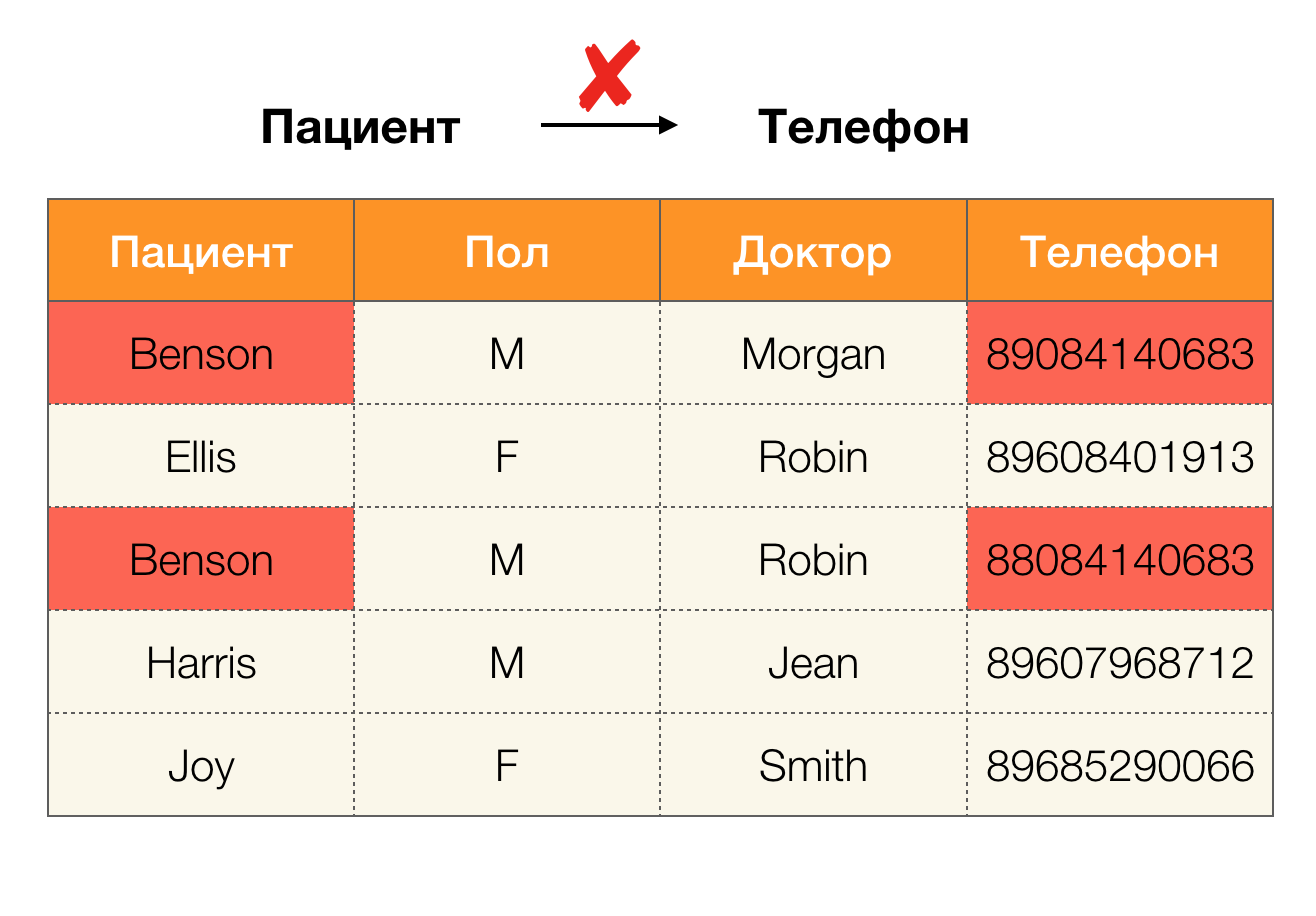
Exemplo de duplicatas nos dados:



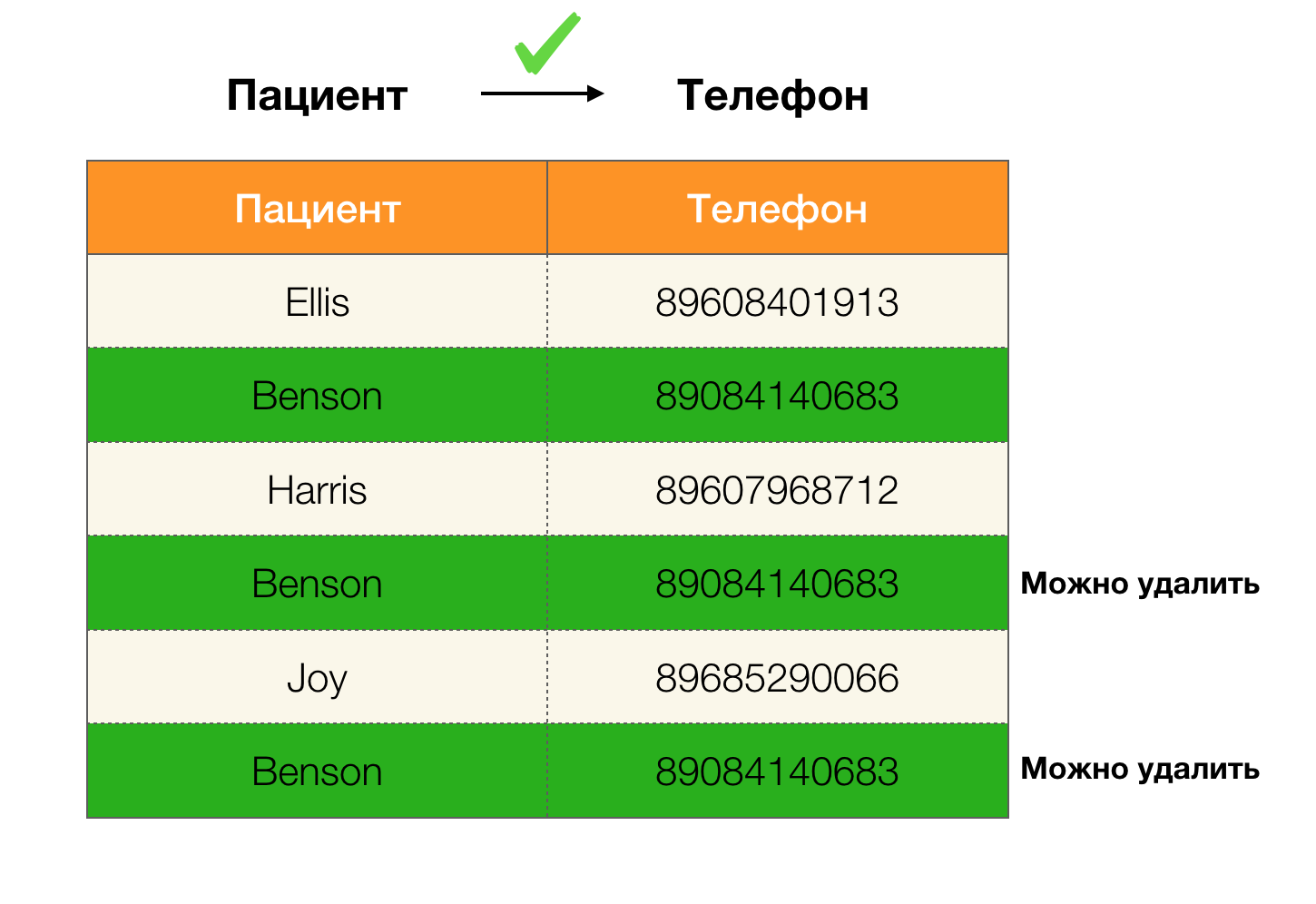
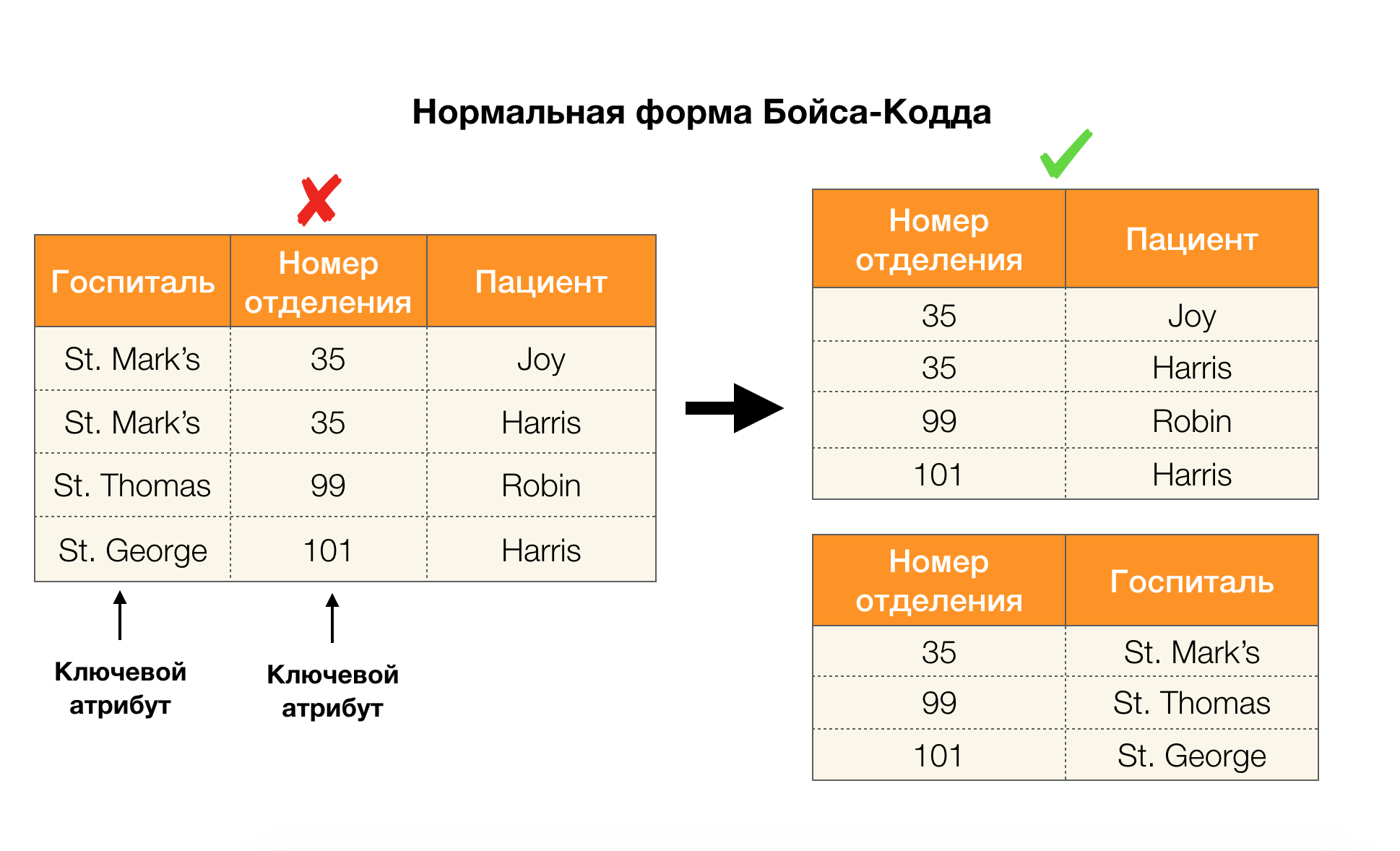
Por exemplo, temos uma tabela e um conjunto de leis federais que devem ser executadas. A limpeza de dados nesse caso envolve a alteração dos dados para que as leis federais estejam corretas. Ao mesmo tempo, o número de modificações deve ser mínimo (para este procedimento, existem algoritmos nos quais não iremos focar neste artigo). A seguir, é apresentado um exemplo dessa conversão de dados. À esquerda está a relação inicial, na qual, obviamente, as Leis Federais necessárias não são cumpridas (um exemplo de violação de uma das Leis Federais é destacado em vermelho). À direita, há uma relação atualizada na qual as células verdes mostram valores alterados. Após esse procedimento, as dependências necessárias começaram a se manter.



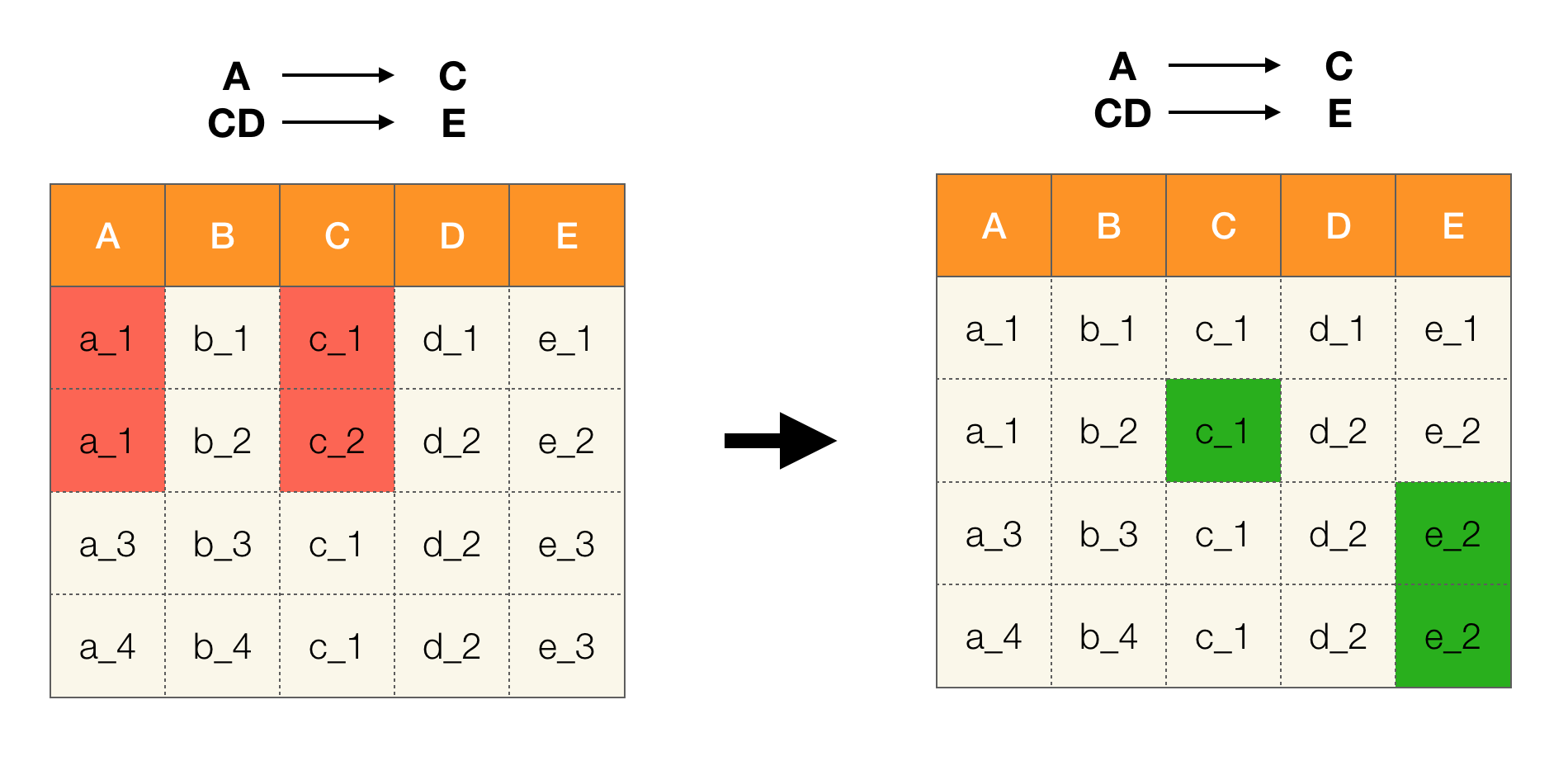
Outra aplicação popular é o design de banco de dados. Aqui vale a pena lembrar sobre formas normais e normalização. Normalização é o processo de alinhar um relacionamento com um determinado conjunto de requisitos, cada um dos quais é determinado à sua maneira por uma forma normal. Não escreveremos os requisitos de várias formas normais (isso é feito em qualquer livro do curso de DB para iniciantes), mas apenas observamos que cada um deles usa o conceito de dependências funcionais à sua maneira. De fato, as leis federais são inerentemente restrições de integridade que são levadas em consideração ao projetar um banco de dados (no contexto dessa tarefa, as leis federais são às vezes chamadas de superchaves).

Considere a aplicação dos quatro formulários normais na figura abaixo. Lembre-se de que o formulário normal de Boyce-Codd é mais rigoroso que o terceiro, mas menos rigoroso que o quarto. Ainda não consideramos o último, uma vez que sua formulação requer um entendimento de dependências com vários valores, que não são de interesse para nós neste artigo.






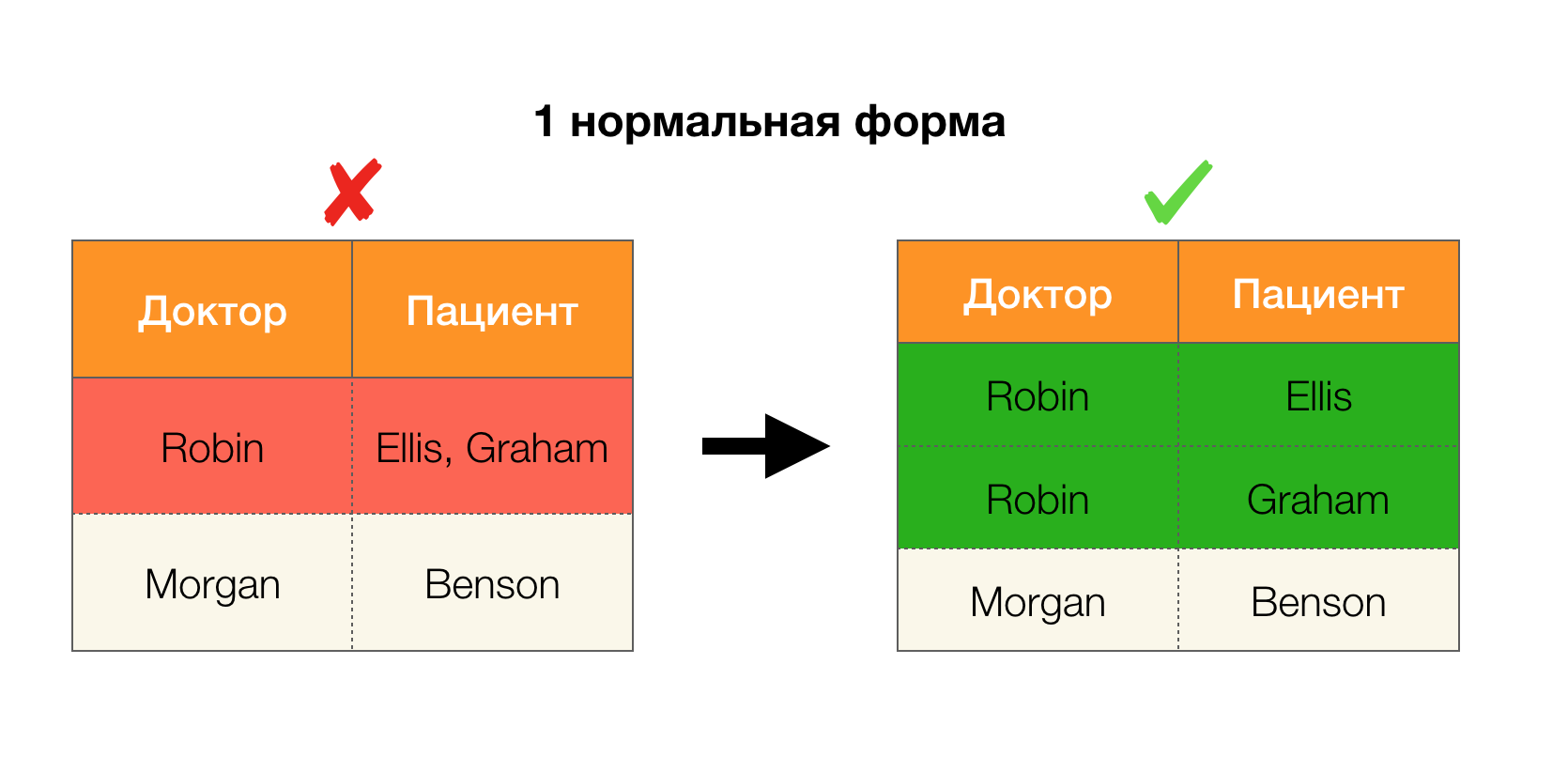
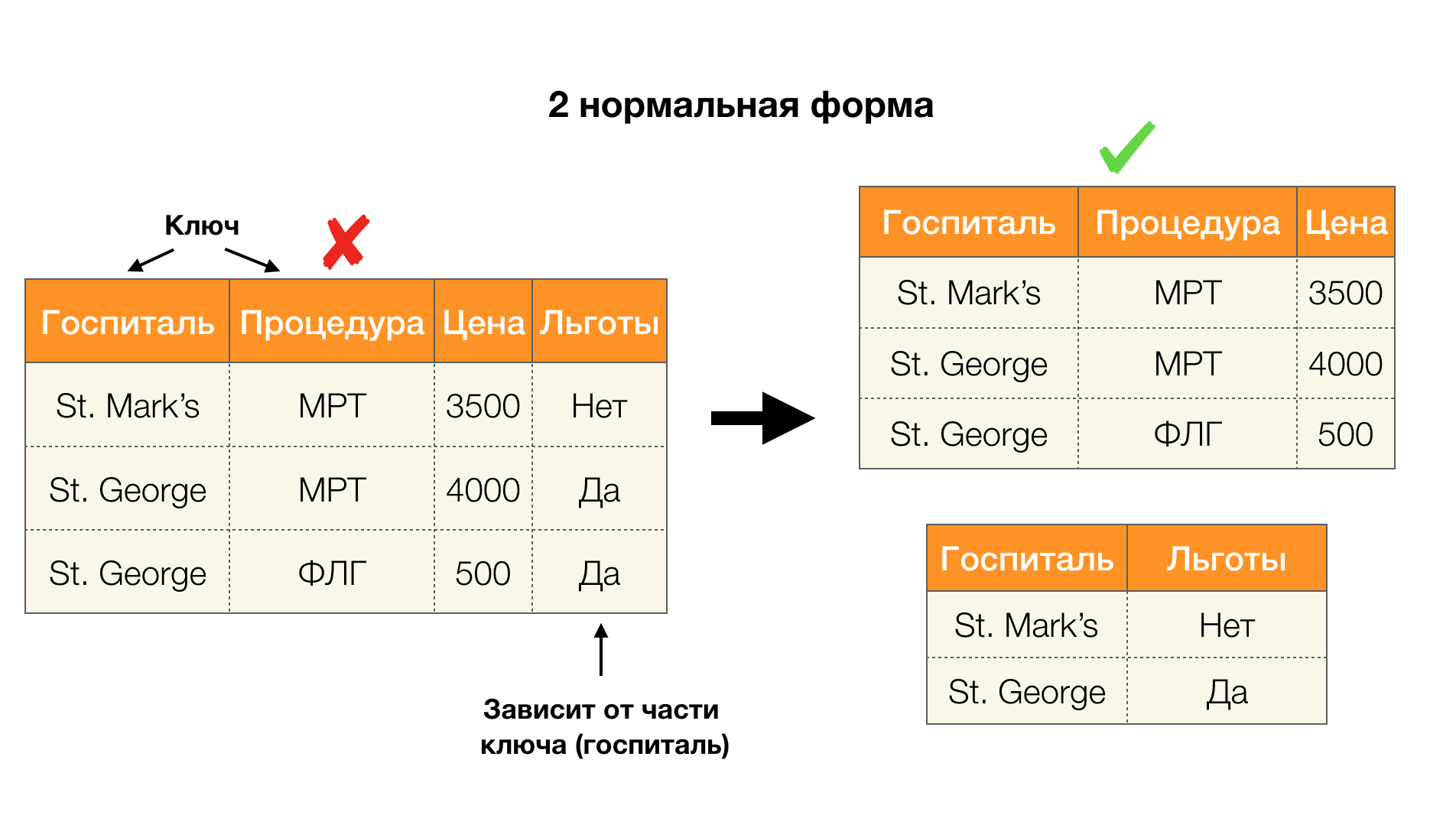
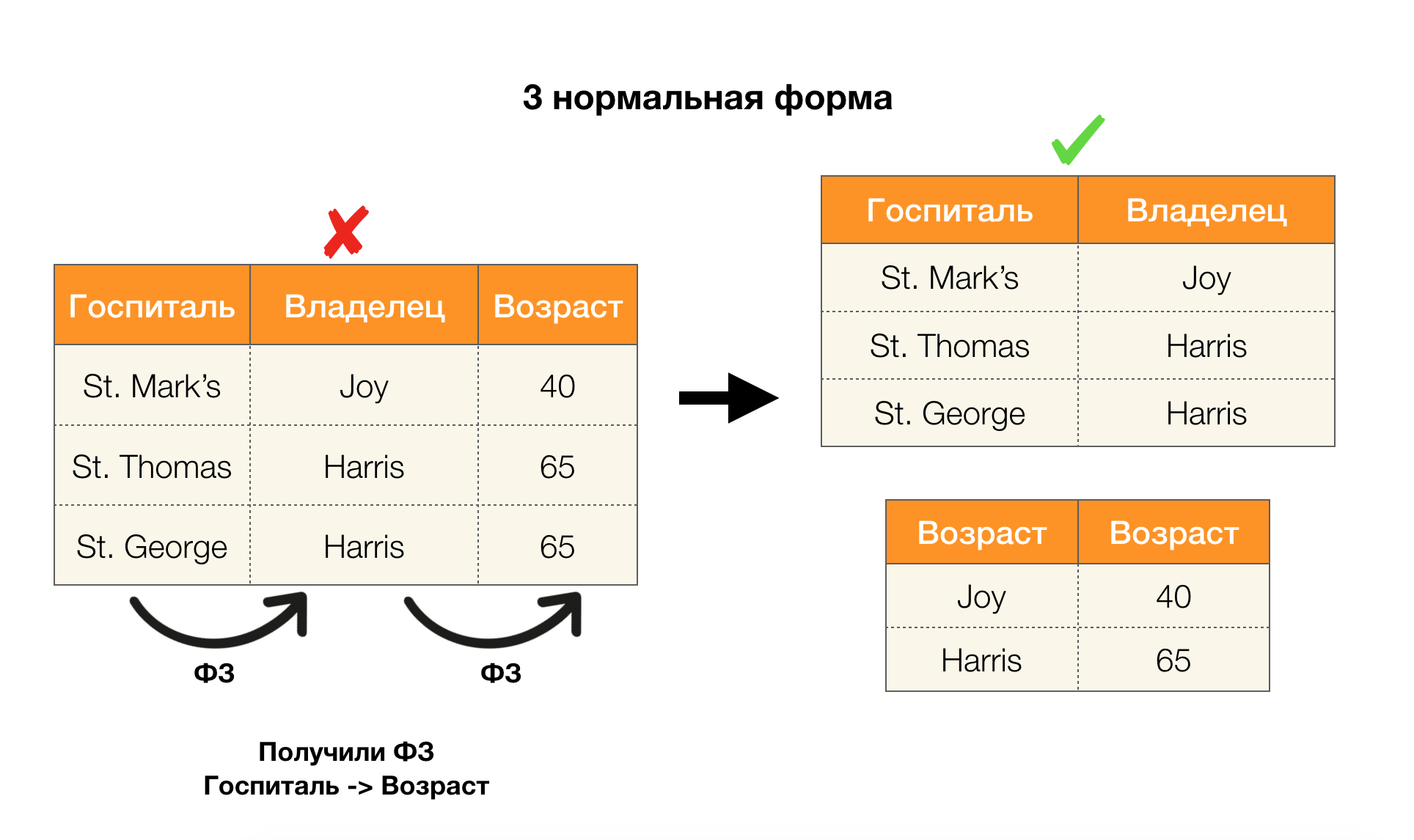
Outra área em que as dependências encontraram sua aplicação é a redução da dimensão do espaço de feição em tarefas como a construção de um classificador bayesiano ingênuo, a identificação de feições significativas e a reparametrização do modelo de regressão. Nos artigos originais, esse problema é chamado de determinação de recursos redundantes e relevância dos recursos [5, 6] e é resolvido com o uso ativo dos conceitos de banco de dados. Com o advento de tais trabalhos, podemos dizer que hoje existe uma solicitação de soluções que permitem combinar o banco de dados, análises e implementação dos problemas de otimização acima em uma ferramenta [7, 8, 9].

Existem muitos algoritmos (modernos e não muito) para pesquisar a Lei Federal em um conjunto de dados, que podem ser divididos em três grupos:

• Algoritmos usando a travessia de treliças algébricas (algoritmos de travessia de treliça)
• Algoritmos baseados na busca de valores consistentes (algoritmos de diferença e de concordância)
• Algoritmos de comparação em pares (algoritmos de indução de dependência)
  

Uma breve descrição de cada tipo de algoritmo é apresentada na tabela abaixo:


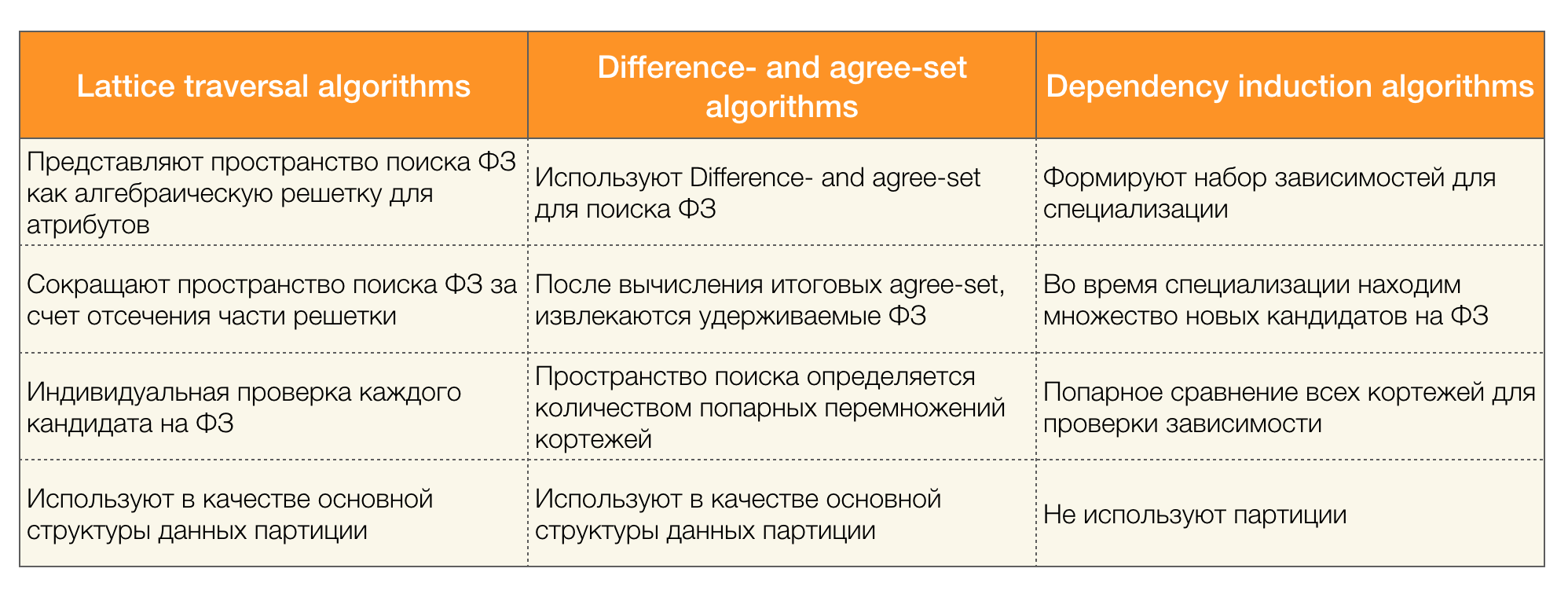
Mais detalhes sobre essa classificação podem ser lidos [4]. Abaixo estão exemplos de algoritmos para cada tipo:





Atualmente, estão surgindo novos algoritmos que combinam várias abordagens para a busca de dependências funcionais ao mesmo tempo. Exemplos de tais algoritmos são Pyro [2] e HyFD [3]. A análise de seu trabalho é esperada nos seguintes artigos desta série. Neste artigo, analisaremos apenas os conceitos básicos e o lema necessários para entender as técnicas para detectar dependências.

Vamos começar com um simples - conjunto de diferenças e concordância, usado no segundo tipo de algoritmos. Conjunto de diferenças é um conjunto de tuplas que não correspondem a valores e conjunto de concordância, pelo contrário, são tuplas que correspondem a valores. Deve-se notar que, neste caso, consideramos apenas o lado esquerdo da dependência.

Também um conceito importante que foi encontrado acima é a rede algébrica. Como muitos algoritmos modernos operam com esse conceito, precisamos ter uma idéia do que é.

Para introduzir o conceito de treliça, é necessário definir um conjunto parcialmente ordenado (ou conjunto parcialmente ordenado, para poste curto).

Definição 2. Diz-se que o conjunto S é parcialmente ordenado pela relação binária ⩽ se para qualquer a, b, c ∈ S forem satisfeitas as seguintes propriedades:

1. Reflexividade, ou seja, a ⩽ a
2. Anti-simetria, isto é, se a ⩽ b e b ⩽ a, então a = b
3. Transitividade, ou seja, para a and b e b ⩽ c, segue-se que a ⩽ c
   

Essa relação é chamada de relação de ordem parcial (não estrita), e o próprio conjunto é chamado de conjunto parcialmente ordenado. Notação formal: ⟨S, ⩽⟩.

Como exemplo mais simples de um conjunto parcialmente ordenado, podemos pegar o conjunto de todos os números naturais N com a relação usual de ordem ⩽. É fácil verificar se todos os axiomas necessários são satisfeitos.

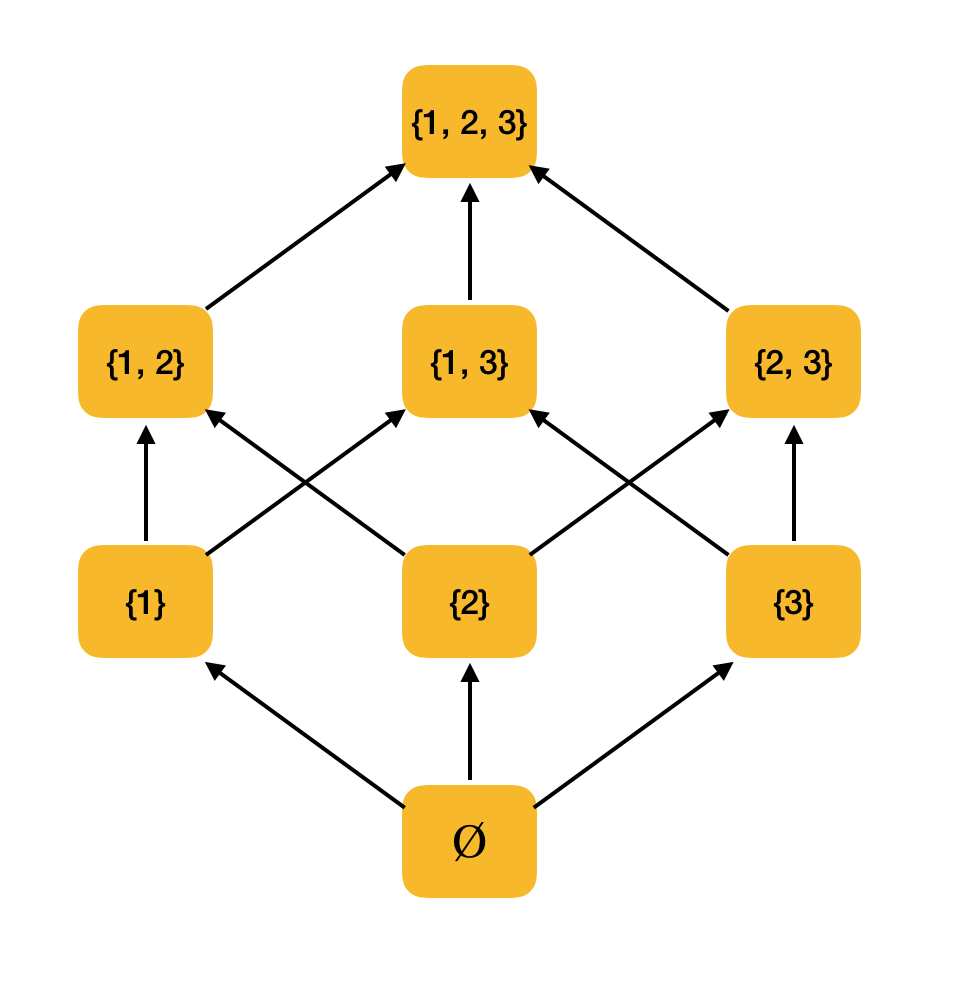
Exemplo mais significativo. Considere o conjunto de todos os subconjuntos {1, 2, 3} ordenados pela relação de inclusão ⊆. De fato, essa relação satisfaz todas as condições de ordem parcial; portanto, ⟨P ({1, 2, 3}), ⊆⟩ é um conjunto parcialmente ordenado. A figura abaixo mostra a estrutura deste conjunto: se de um elemento você pode caminhar ao longo das setas para outro elemento, eles estão em relação à ordem.



Vamos precisar de mais duas definições simples do campo da matemática - supremo e mínimo.

Definição 3. Seja ⟨S ⩽⟩ um conjunto parcialmente ordenado, A ⊆ S. O limite superior de A é um elemento u ∈ S tal que ∀x ∈ A: x ⩽ u. Seja U o conjunto de todos os limites superiores de A. Se U tiver o menor elemento, ele será chamado supremo e será indicado por sup A.

Da mesma forma, o conceito de um limite inferior exato é introduzido.

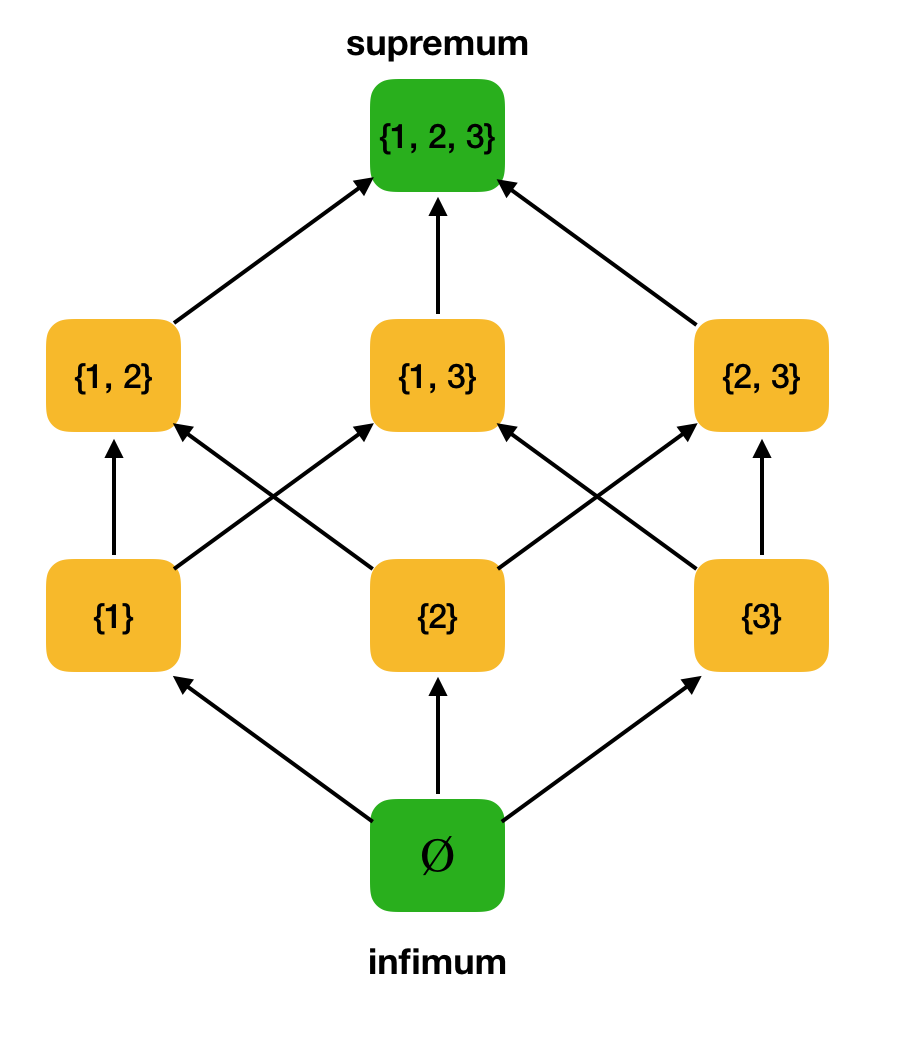
Definição 4. Seja ⟨S ⩽⟩ um conjunto parcialmente ordenado, A ⊆ S. O limite inferior de A é um elemento l ∈ S tal que ∀x ∈ A: l ⩽ x. Seja L o conjunto de todos os limites inferiores de A. Se L tiver o maior elemento, ele será chamado de infimum e será denotado por inf A.

Considere, por exemplo, o conjunto parcialmente ordenado acima ⟨P ({1, 2, 3}), depois e encontre o supremo e o mínimo nele:



Agora podemos formular a definição de uma rede algébrica.

Definição 5. Seja ⟨P, ⩽⟩ um conjunto parcialmente ordenado, de modo que todo subconjunto de dois elementos tenha limites exatos superior e inferior. Então P é chamado de treliça algébrica. Além disso, sup {x, y} é escrito como x ∨ y, e inf {x, y} - como x ∧ y.

Verificamos que nosso exemplo de trabalho ⟨P ({1, 2, 3}), ⊆⟩ é uma treliça. De fato, para qualquer a, b ∈ P ({1, 2, 3}), a∨b = a∪b e a∧b = a∩b. Por exemplo, considere os conjuntos {1, 2} e {1, 3} e encontre seu máximo e supremo. Se cruzá-los, obtemos o conjunto {1}, que será o mínimo. Nós obtemos o supremo por sua união - {1, 2, 3}.

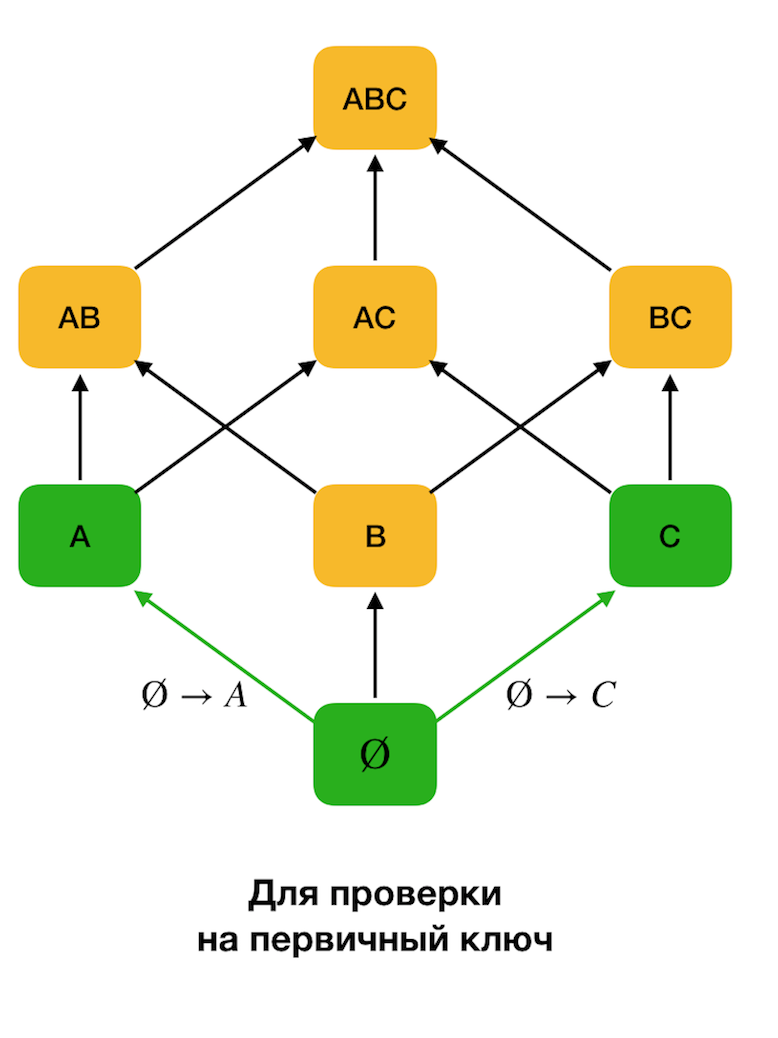
Nos algoritmos de detecção de FD, o espaço de pesquisa é frequentemente representado na forma de uma rede, onde conjuntos de um elemento (leia o primeiro nível da rede de pesquisa, onde a parte esquerda das dependências consiste em um atributo) são cada atributo do relacionamento original.
No início, as dependências do formulário form → Atributo único são consideradas. Esta etapa permite determinar quais atributos são chaves primárias (não há determinantes para esses atributos e, portanto, o lado esquerdo está vazio). Além disso, esses algoritmos sobem na rede. Vale ressaltar que a rede não pode ser ignorada por todos, ou seja, se o tamanho máximo desejado da parte esquerda for transmitido para a entrada, o algoritmo não irá além do nível com esse tamanho.

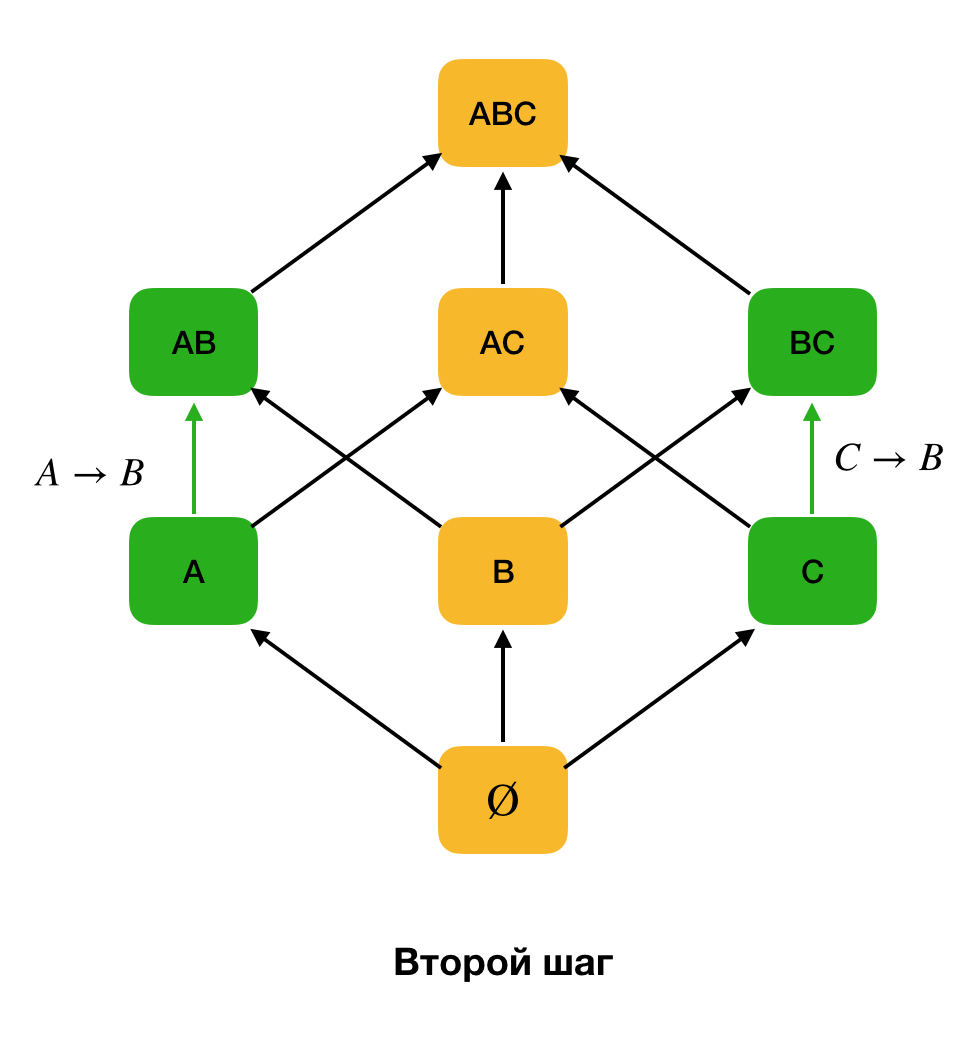
A figura abaixo mostra como você pode usar a rede algébrica no problema de pesquisa da Lei Federal. Aqui, cada aresta ( X, XY ) representa uma dependência X → Y. Por exemplo, passamos pelo primeiro nível e sabemos que a dependência A → B é mantida (mostraremos isso pela conexão verde entre os vértices A e B ). Portanto, quando subimos a rede para cima, não podemos verificar a dependência A, C → B , porque ela não será mais mínima. Da mesma forma, não o testaríamos se a dependência C → B fosse mantida.




Além disso, como regra, todos os algoritmos modernos de pesquisa FZ usam essa estrutura de dados como uma partição (partição removida [1] na fonte original). A definição formal de partição é a seguinte:

Definição 6. Seja X ⊆ R o conjunto de atributos para a relação r. Um cluster é um conjunto de índices de tuplas de r que têm o mesmo valor para X, ou seja, c (t) = {i | ti [X] = t [X]}. Partição é um conjunto de clusters, excluindo clusters de comprimento de unidade:

$$

$$\ pi (X): = \ {c (t) | t \ in r \ wedge | c (t) | > 1 \}$$

Em palavras simples, a partição para o atributo X é um conjunto de listas, em que cada lista contém números de linhas com os mesmos valores para X. Na literatura moderna, uma estrutura representando partições é chamada de índice de lista de posições (PLI). Clusters de comprimento de unidade são excluídos para compactação PLI porque são clusters que contêm apenas um número de registro com um valor exclusivo que sempre será fácil de configurar.

Considere um exemplo. Vamos voltar à mesma tabela com os pacientes e criar partições para as colunas Patient e Paul (uma nova coluna apareceu à esquerda, na qual os números de linha da tabela estão marcados):





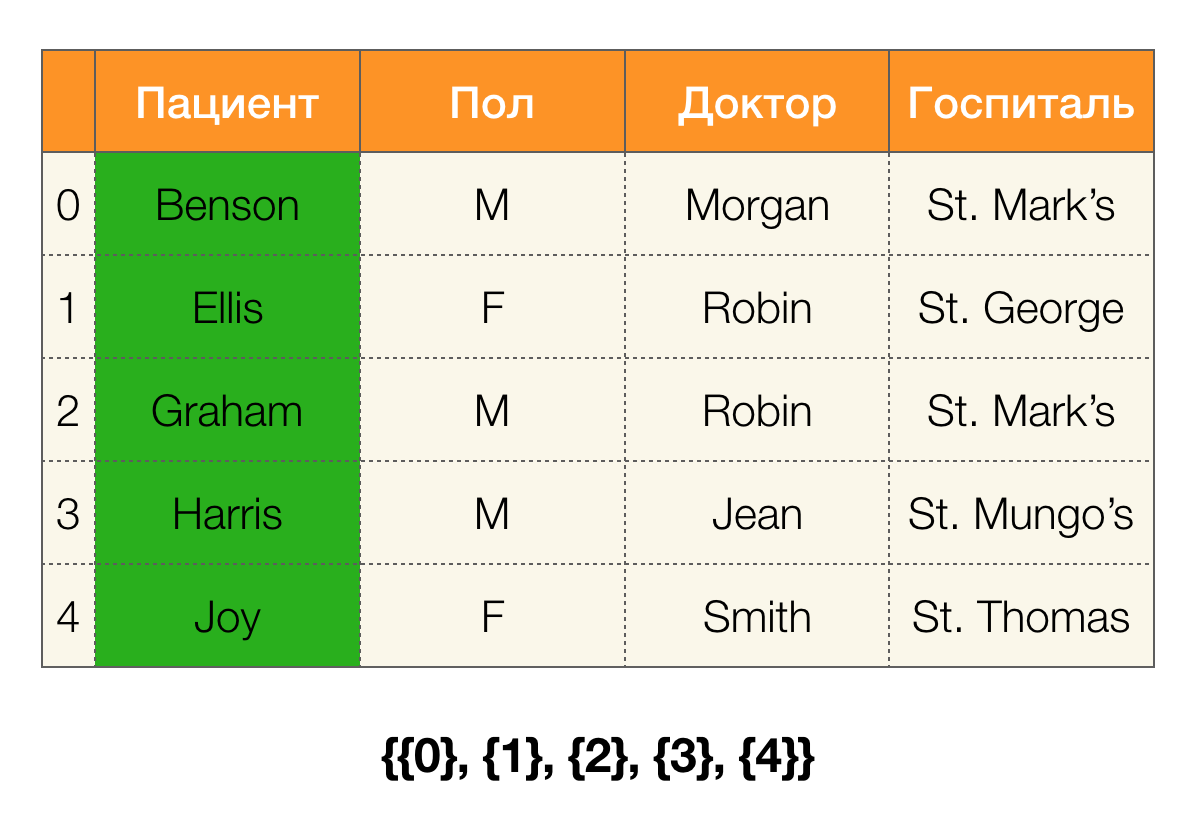
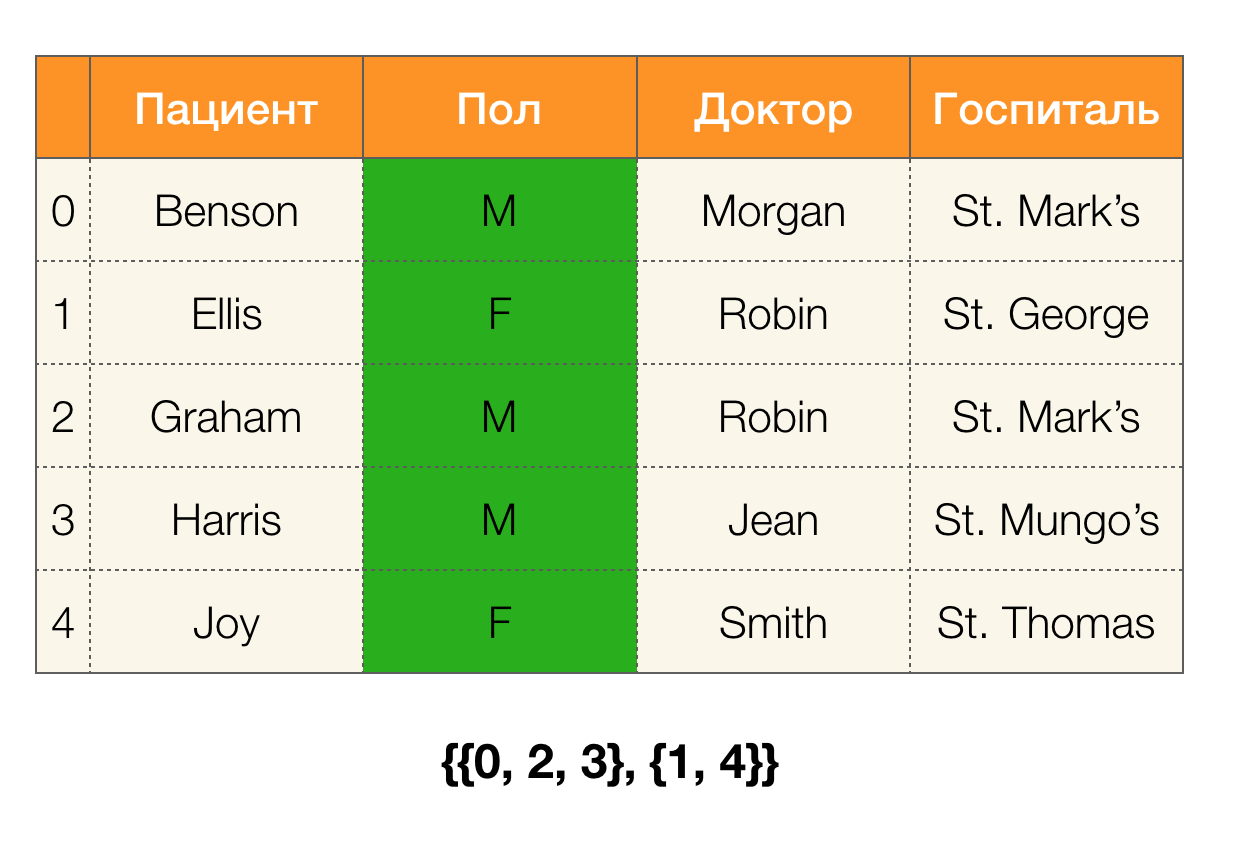
Além disso, de acordo com a definição, a partição da coluna Paciente estará realmente vazia, uma vez que clusters únicos são excluídos da partição.

Partições podem ser obtidas por vários atributos. E para isso, existem duas maneiras: percorrer a tabela, criar uma partição de uma só vez, de acordo com todos os atributos necessários, ou construí-la usando a operação de cruzar partições ao longo de um subconjunto de atributos. Os algoritmos de busca FZ usam a segunda opção.

Em palavras simples, por exemplo, para obter uma partição por colunas ABC , você pode pegar partições para AC e B (ou qualquer outro conjunto de subconjuntos disjuntos) e interceptá-las. A operação de interseção de duas partições identifica clusters de maior comprimento comum a ambas as partições.

Vejamos um exemplo:





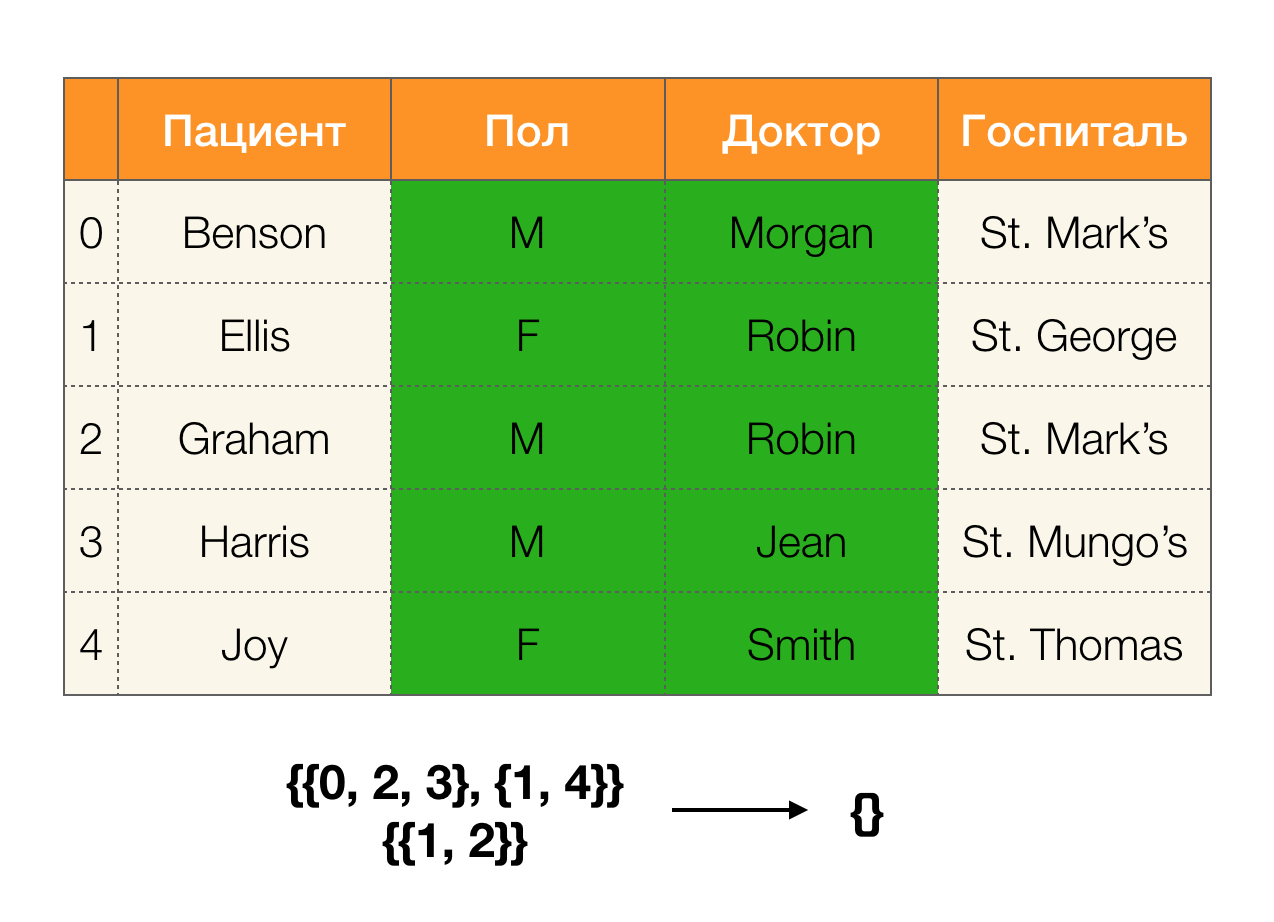
No primeiro caso, recebemos uma partição vazia. Se você olhar atentamente para a tabela, na verdade, os valores idênticos para os dois atributos não estarão lá. Se modificarmos ligeiramente a tabela (o caso à direita), já teremos um cruzamento não vazio. Ao mesmo tempo, as linhas 1 e 2 realmente contêm os mesmos valores para os atributos Paul e Doctor .

Em seguida, precisamos de um conceito como o tamanho da partição. Formalmente:

$$

$$| \ pi (X) | = | \ {c \ in \ pi (X): | c | > 1 \} |$$

Simplificando, o tamanho da partição é o número de clusters incluídos na partição (lembre-se de que clusters individuais não estão incluídos na partição!):





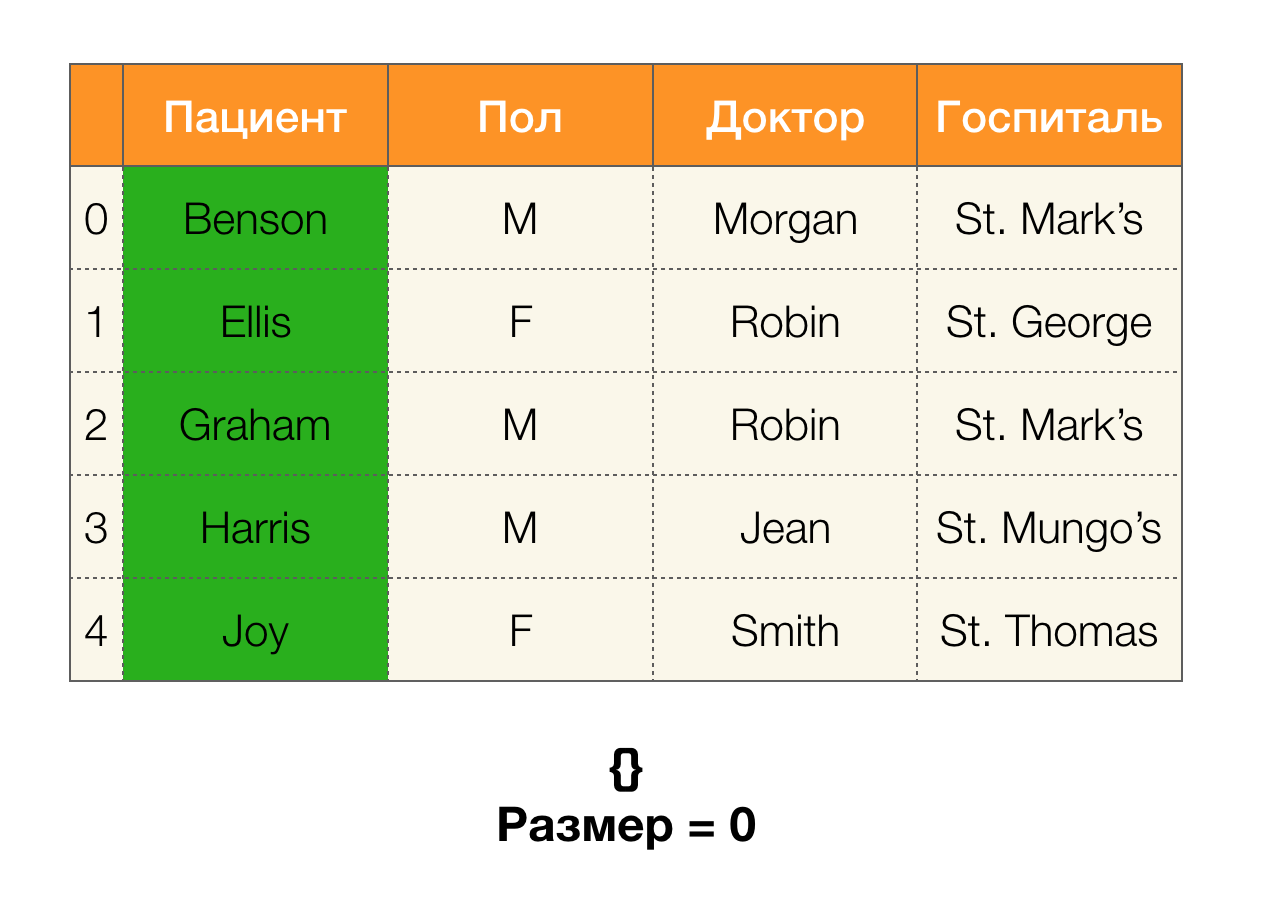
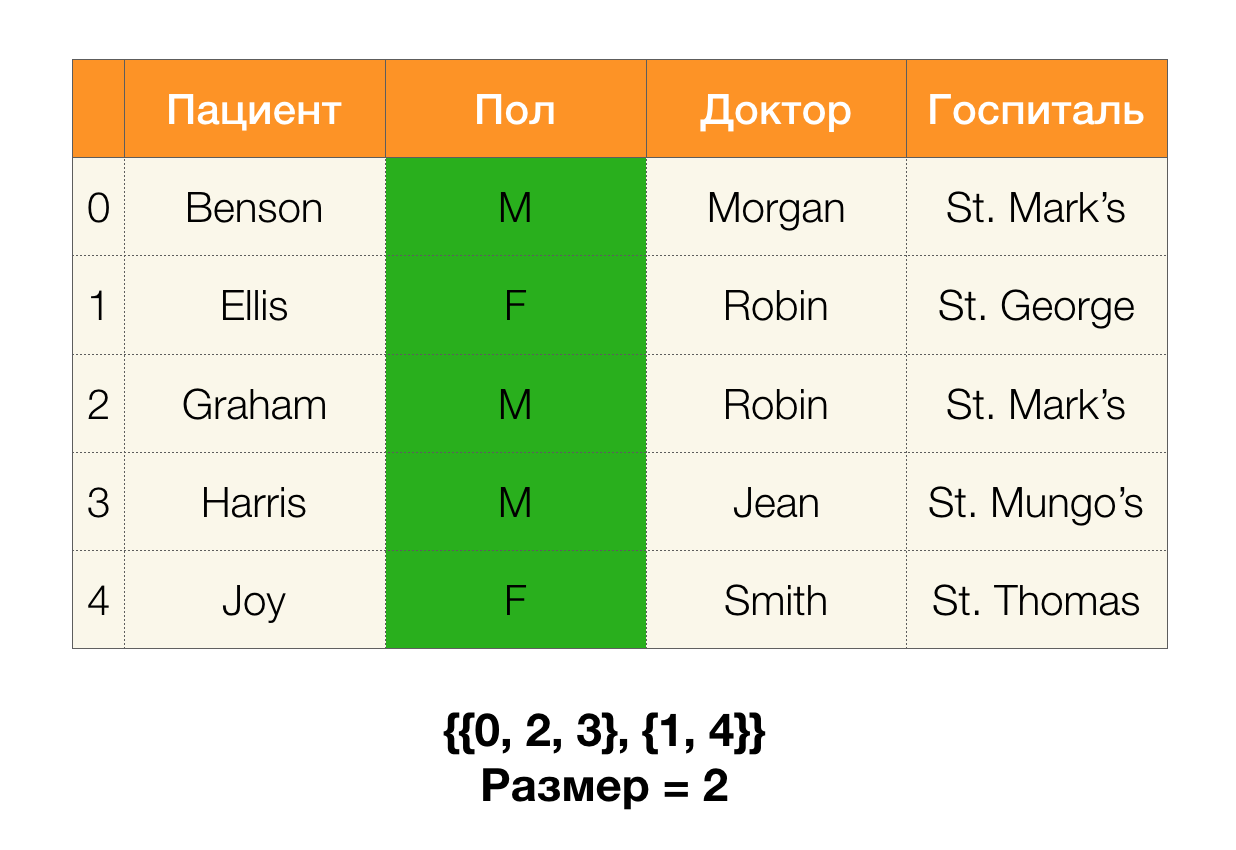
Agora podemos definir um dos principais lemas, que para determinadas partições nos permite estabelecer se a dependência é mantida ou não:

Lema 1 . A dependência A, B → C é mantida se e somente se

$$

$$| \ pi (AB) | = | \ pi (AB \ cup \ {C \}) |$$

De acordo com o lema, para determinar se uma dependência é mantida, é necessário executar quatro etapas:

1. Calcular a partição para o lado esquerdo da dependência
2. Calcular a partição para o lado direito da dependência
3. Calcular o produto da primeira e segunda etapas
   
4. Compare os tamanhos das partições obtidas na primeira e na terceira etapa
   

A seguir, é apresentado um exemplo de verificação se a dependência é mantida por esse lema:






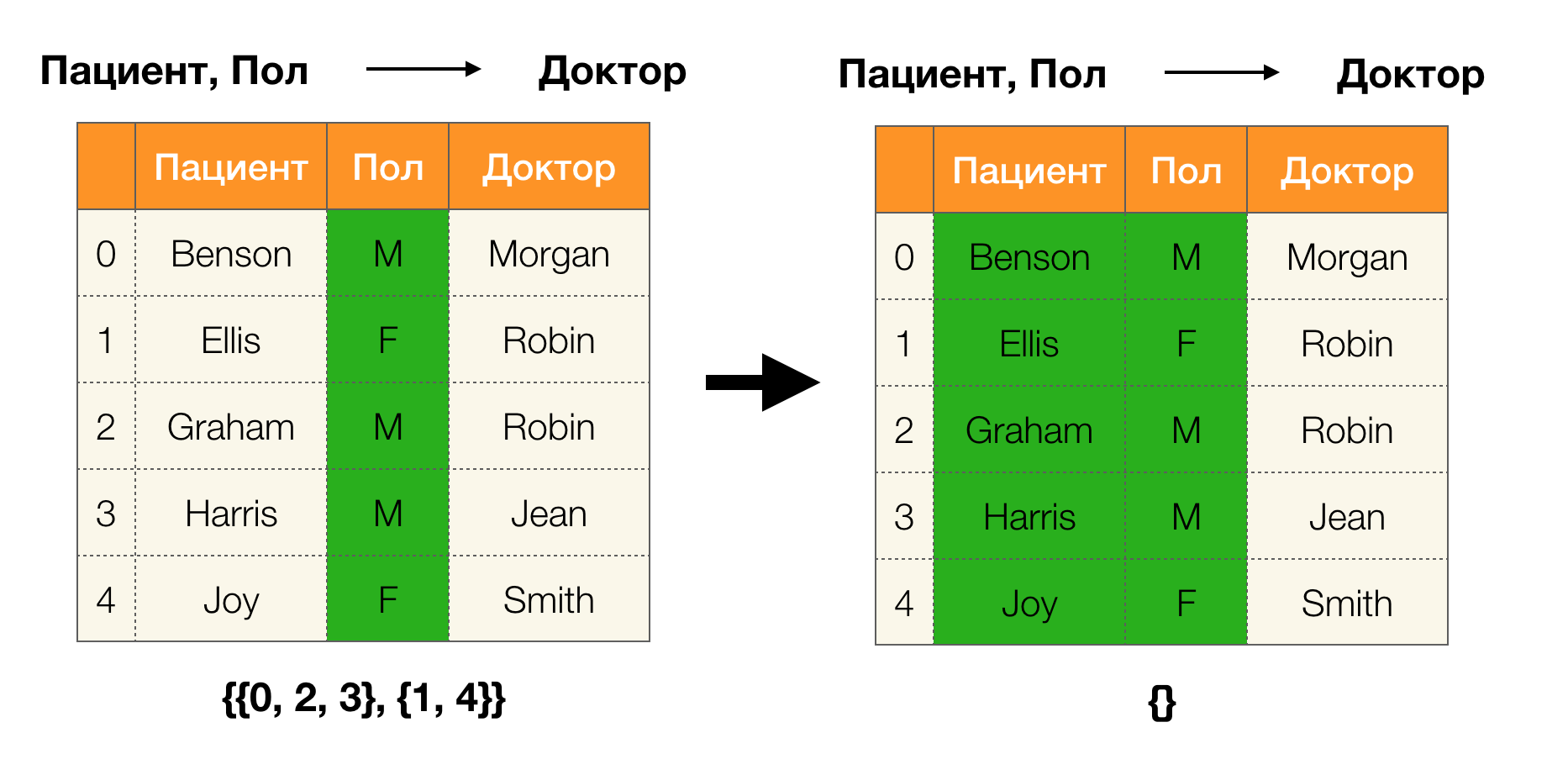
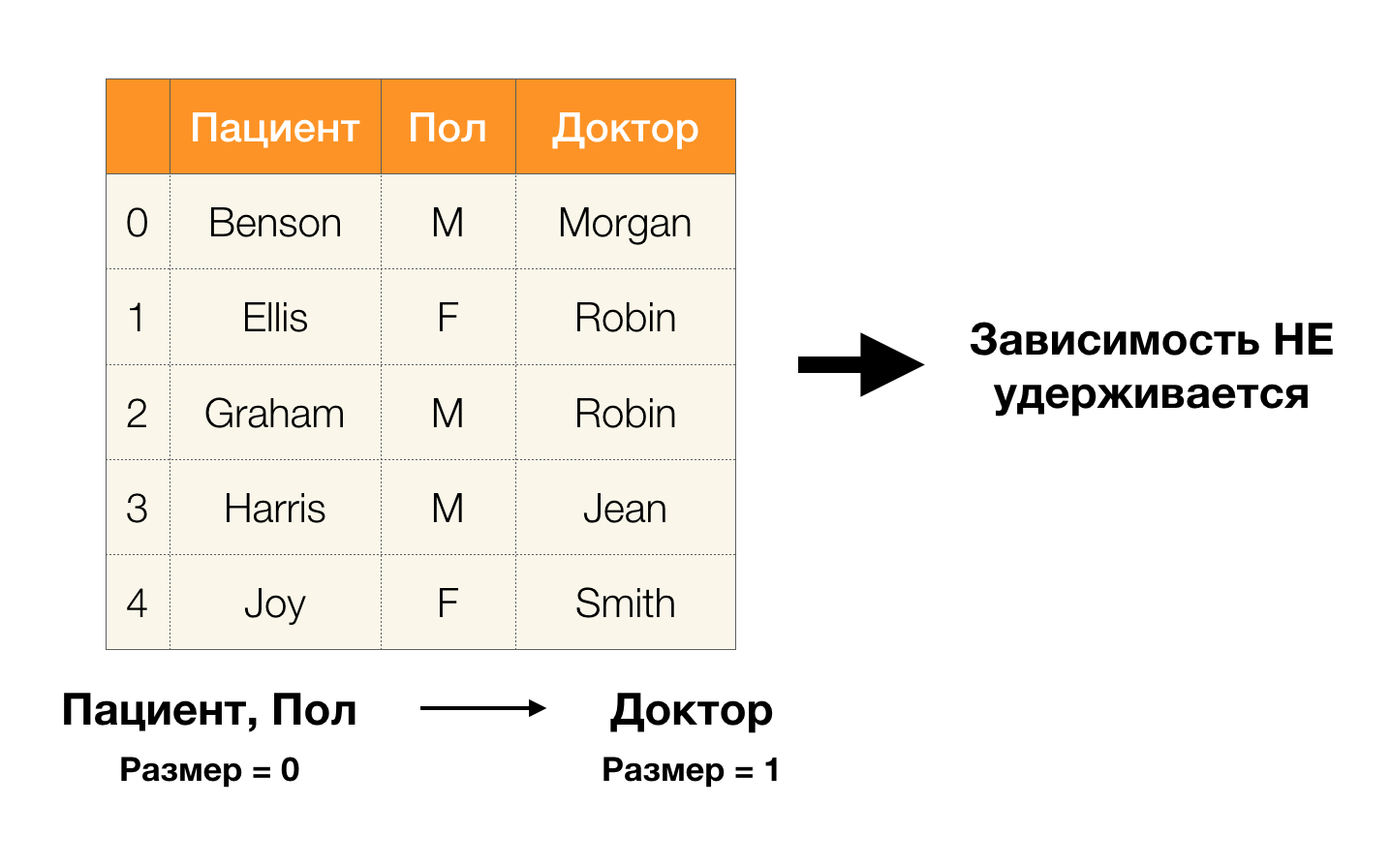
Neste artigo, examinamos conceitos como dependência funcional, dependência funcional aproximada, examinamos onde são utilizados e quais algoritmos de busca para a Lei Federal existem. Também examinamos em detalhes os conceitos básicos, mas importantes, usados ​​ativamente em algoritmos modernos para a busca de leis federais.

Referências à literatura:

1. Huhtala Y. et al. TANE: Um algoritmo eficiente para descobrir dependências funcionais e aproximadas // The journal of computer. - 1999. - T. 42. - Não. 2. - S. 100-111.
2. Kruse S., Naumann F. Descoberta eficiente de dependências aproximadas // Anais da doação VLDB. - 2018. - T. 11. - Não. 7. - S. 759-772.
3. Papenbrock T., Naumann F. Uma abordagem híbrida para a descoberta de dependências funcionais // Anais da Conferência Internacional de 2016 sobre Gerenciamento de Dados. - ACM, 2016 .-- S. 821-833.
4. Papenbrock T. et al. Descoberta de dependências funcionais: uma avaliação experimental de sete algoritmos // Procedimentos da doação de VLDB. - 2015. - T. 8. - Não. 10. - S. 1082-1093.
5. Kumar A. et al. Para ingressar ou não?: Pensar duas vezes antes de ingressar antes da seleção dos recursos // Anais da Conferência Internacional de 2016 sobre Gerenciamento de Dados. - ACM, 2016 - S. 19-34.
6. Abo Khamis M. et al. Aprendizado em banco de dados com tensores esparsos // Anais do 37º Simpósio ACM SIGMOD-SIGACT-SIGAI sobre Princípios de Sistemas de Banco de Dados. - ACM, 2018 - S. 325-340.
7. Hellerstein JM et al. A biblioteca de análise do MADlib: ou habilidades do MAD, o SQL // Procedimentos da doação do VLDB. - 2012. - T. 5. - Não. 12. - S. 1700-1711.
8. Qin C., Rusu F. Aproximações especulativas para otimização de descida em gradiente distribuído em escala teraescala // Anais do Quarto Workshop sobre Análise de Dados na Nuvem. - ACM, 2015 - S. 1.
9. Meng X. et al. Mllib: aprendizado de máquina no apache spark // The Journal of Machine Learning Research. - 2016. - T. 17. - Não. 1 - S. 1235-1241.

: , JetBrains Research , CS , JetBrains Research