Pouco mais de um ano se passou desde que o MIT anunciou o lançamento da linguagem de propósito geral de alto desempenho Julia . Desde então, o idioma ganhou popularidade: é usado em mais de 1.500 universidades (em algumas é ensinado como o primeiro idioma da instrução), e os campos de aplicação abrangem desde diagnósticos médicos e planejamento de missões espaciais até problemas prementes, como otimizar o tráfego de ônibus escolar .
Um dos principais campos de atividade de muitos projetos, não é difícil adivinhar, é o aprendizado de máquina, para o qual Julia possui muitas ferramentas poderosas , e um projeto bastante interessante foi publicado recentemente - o General Probability Programming System “GEN” .
Hoje vamos prestar atenção, como o nome indica, ao pacote Flux , que fornece todo o poder das redes neurais. Vamos tentar passar do processamento e pesquisa de conjuntos de imagens para uma rede neural treinada para obter um classificador completo!
Instalação
Faça o download do kit de distribuição no site oficial e instale o interpretador Julia ( REPL ) no seu computador.
Para que o gerenciador de pacotes funcione corretamente, os usuários do Windows 7 / Windows Server 2012 também devem instalar:
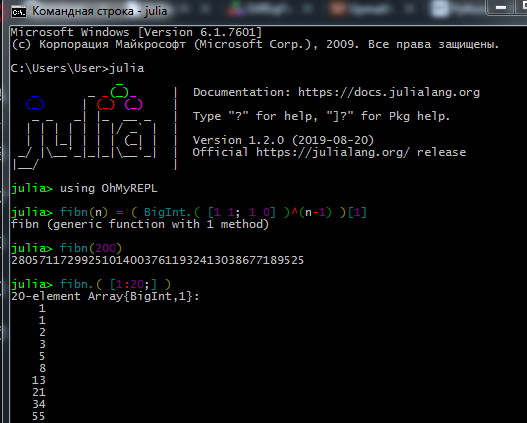
O processo de trabalho no REPL é mais ou menos assim:
Verdadeiros dataayantists e machine-lingologists preferem Jupyter . Aqui, você pode ver a instalação e encontrar lições interativas para estudos independentes, com tarefas em russo (links para os tutoriais originais e um guia para o idioma).
Aqui você pode ver como trabalhar com o Jupyter Notebook.
Se houver problemas de instalação- A conexão não pode ser estabelecida - verifique seus direitos de acesso (você tem restrições para gravar em pastas em C: \, faça login como administrador ou inicie Julia no modo de administrador); se estiver usando um proxy, verifique se ele está configurado não apenas para o navegador
- Alguns pacotes não gostam do alfabeto cirílico no caminho do arquivo; portanto, devido ao nome de usuário em russo, tive muitos problemas
- Se o pacote Interact não exibir resultados, você pode ter instalado o WebIO incorretamente, o que pode ser corrigido
- Para alguns pacotes funcionarem corretamente no Windows, os caminhos para Julia e Jupyter devem ser inseridos nas variáveis de ambiente.
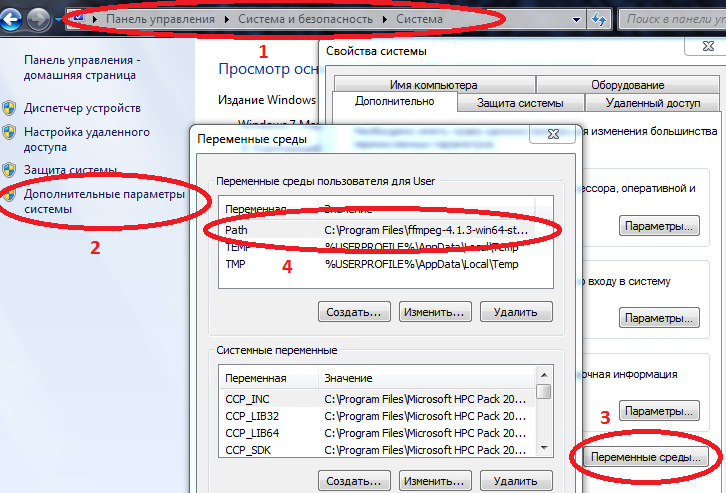
Computador / Propriedades do sistema / Parâmetros avançados do sistema / Variáveis de ambiente / Caminho (crie se não for) e adicione o caminho a julia.exe lá
Exemplo C: \ Usuários \ Usuário \ AppData \ Local \ Julia-1.2.0 \ bin
se Path já tiver valores, separe-os com um ponto e vírgula.
Agora, se você conduzir julia no console de comandos ( cmd ), o intérprete será iniciado.
Depois de instalar tudo o que você precisa, você pode continuar o download dos pacotes necessários hoje. Digite comandos no REPL ou Jupyter
Código using Pkg pkgs = ["Plots", "TextParse", "CSV", "DataFrames", "ImageMagick", "Images", "Interact", "Flux"] for p in pkgs Pkg.add(p) end for p in pkgs Pkg.build(p) end
Depois de aprender o básico do idioma (trabalhando com matrizes, criando funções, fazendo download de pacotes, plotando gráficos), você pode prosseguir para o material subsequente.
Carregamento e processamento de dados
Coletar e organizar dados é uma arte separada. Em relação à Julia, a rede possui muito material desatualizado, mas primeiro você pode tentar o tutorial acima e, para um estudo mais aprofundado, ler o livro Data Science with Julia (em domínio público)
E hoje, talvez, trabalharemos com dados já preparados: um conjunto de dados de um grande número de fotografias de frutas de vários ângulos - quem queria uma fruta fresca?


Na verdade, esta é a tarefa - ensinaremos a rede neural a distinguir maçãs de bananas!
Primeiramente, faça o upload de algumas imagens de teste:
using Images fnames = [ "data/10_100.jpg", "data/107_100.jpg", "data/yellow_apple_2.jpg", "data/8_100.jpg", "data/104_100.jpg", "data/3_100.jpg" ]

Como os objetos nas figuras diferem entre si? Primeiro, pela forma, depois pela cor e depois pelas texturas e outros atributos. A análise de imagens é um tópico interessante por si só, e a classificação pode ser feita não apenas por neurônios, mas também, digamos, por wavelets . Começaremos com a cor do sinal mais simples.
Como você sabe, as imagens são armazenadas na memória do computador na forma de matrizes; no nosso caso, são matrizes, cada célula contendo três números, indicando a quantidade de cores vermelha, verde e azul em cada pixel da imagem. Vamos ver a quantidade média de cada cor nestas imagens:
using Statistics: mean M1 = [ mean(float.(c.(img))) for c = [red,green,blue], img = fruits ] 3×6 Array{Float32,2}: 0.570278 0.652852 0.977111 0.835252 0.903998 0.842564 0.338118 0.468729 0.950773 0.806882 0.880692 0.755442 0.322406 0.379424 0.835212 0.707626 0.799643 0.761916
Analisamos cuidadosamente a primeira linha - não incomoda você? Uma maçã amarela e bananas são mais vermelhas que as maçãs da variedade Breburn! Como assim ?! Vamos lá, crie minas azedas, talvez os alunos estejam lendo este tutorial, ou alunos mais jovens do Ballet and Tractor Institute. Portanto, tentaremos evitar omissões. O fato é que o fundo de cada imagem é branco e, na notação RGB , é representado pelos valores (1,1,1). E como existem mais 6 planos de fundo nas 3 imagens de traço, além da cor das bananas e da maçã amarela também conterem cor vermelha, as duas primeiras fotos perdem em vermelho. Para maior clareza, dividimos as imagens em cores básicas:
function tweaking(img) R = colorview( RGB, red.(img),zeroarray,zeroarray ) G = colorview( RGB, zeroarray,green.(img),zeroarray ) B = colorview( RGB, zeroarray,zeroarray, blue.(img) ) [R; G; B] end tweaking( hcat(fruits...) )

Você já ouviu a palavra enigmática "base"? Portanto, podemos dizer que essas imagens são dispostas em uma base RGB . Quanto mais preto - menos uma determinada cor e, como esperávamos, o fundo com sua riqueza torna barulhento o cálculo das médias. Exclua.
function remove_background(img) mtrx = copy( channelview(img) ) for i = 1:size(mtrx, 2), j = 1:size(mtrx, 3) if reduce(&, mtrx[:,i,j] .> [0.8, 0.8, 0.8])

M3 = [ mean(float.(c.(img))) for c = [red,green,blue], img = greyfruits ] 3×6 Array{Float32,2}: 0.451008 0.532696 0.578967 0.527727 0.52849 0.500276 0.218805 0.348609 0.552679 0.499192 0.505136 0.412946 0.203528 0.260142 0.439354 0.400631 0.424784 0.419291
A diferença na área ocupada por cada objeto ainda está afetando, mas, em geral, pode-se concluir que as bananas são maçãs mais verdes ( e azuis ). Este será o critério de avaliação, ou seja, um sinal. Agora vamos dar uma olhada no restante das fotos:
pth = "C:\\Users\\User\\Desktop\\Banana"
Para cada imagem, neutralizamos a contribuição do plano de fundo, encontramos a quantidade média de cada cor, lembrando simultaneamente os tamanhos da imagem ...
dataz = [] for fname in fnames img_i = load("$pth\\$fname") gbimg = remove_background(img_i) colorz = [ mean(c.(gbimg)) for c = [red,green,blue] ] inform = [size(gbimg, 1) size(gbimg, 2) colorz' ] push!(dataz, inform) end dataz
... e então você pode organizar nossos dados em estruturas convenientes para o trabalho - quadros de dados:
using DataFrames, CSV banans = DataFrame( vcat(dataz...), [:height, :width, :red, :green, :blue] ) CSV.write("data/bananas.csv", banans)
apples = CSV.read("data/Apple_Braeburn.csv")
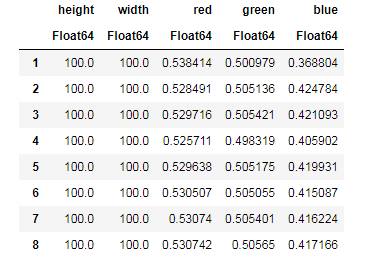
Desc = describe(apples, :all)
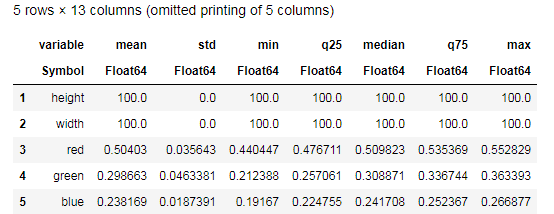
Tente compreender os dados fornecidos pela função describe() e compare com uma tabela semelhante para bananas. Bem, que tipo de análise de dados pode ser sem gráficos?
function plot2features(clr) x_apples = apples[:, :green] x_banans = banans[:, :green] y_apples = apples[:, clr] y_banans = banans[:, clr] scatter(x_apples, y_apples, lab = "apples", colour = :red) scatter!(x_banans, y_banans, lab = "bananas", legend = :topleft, colour = :yellow) hline!([mean(y_apples), mean(y_banans) ], lab = "" ) vline!([mean(x_apples), mean(x_banans) ], lab = "" ) xaxis!("green") yaxis!("$clr") end plot2features(:red)
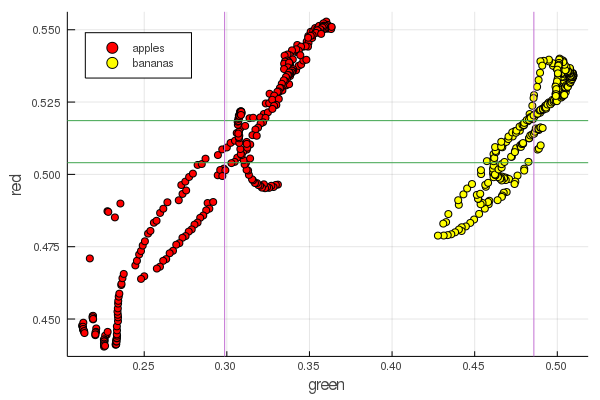
plot2features(:blue)
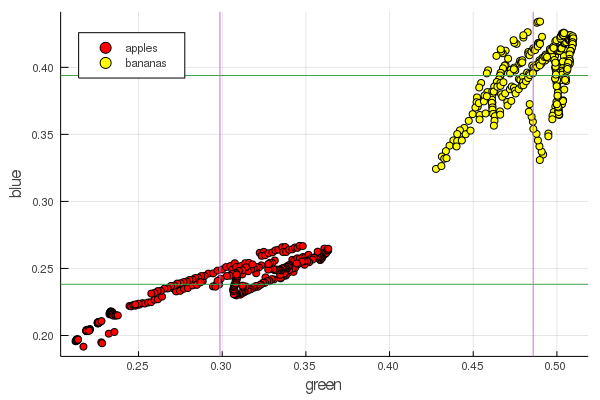
O vermelho médio da banana é muito próximo em valor ao meio da maçã. Porém, no segundo gráfico, o isolamento dos frutos é imediatamente mais claramente traçado por duas características de cor ao mesmo tempo. As separações podem ser melhoradas pela renormalização correta, por exemplo, nossos valores de verde mudam de 0,2 para 0,55 e, se você realizar a conversão
x′i= fracxi− min(x) max(x)− min(x)
então, os dados são redimensionados em [0,1], o que aumentará a diferença entre esses montões aglomerados de pontos.
Perceptron
A tarefa de classificação consiste em definir um modelo e selecionar parâmetros para os quais vários dados receberão uma avaliação exclusiva de sua pertença a uma classe específica. Simplificando, precisamos introduzir uma certa função e definir seus parâmetros para separar nossas maçãs das bananas.
O modelo mais famoso e popular para esses fins é o neurônio artificial McCulloch-Pitts, desenvolvido no início da década de 1940. Posteriormente, Frank Rosenblatt propôs uma rede neural treinada - o perceptron. Não é difícil encontrar explicações abrangentes sobre redes neurais, inclusive sobre este recurso (por exemplo, redes neurais para iniciantes , uso de redes neurais no reconhecimento de imagens , redes neurais, princípios fundamentais de operação, variedade e topologia )
Selecionando o sigmóide como função de ativação e configurando as saídas dos objetos classificados (frutas) de acordo com suas saídas
sigma(x;w,b):= frac11+ exp(−wx+b)
x= mathrmdata
sigma(x;w,b) aproximadamente0 implica mathrmapple
sigma(x;w,b) aproximadamente1 implica mathrmbanana
selecione esses parâmetros W e b de modo que os valores de saída do sigmóide para os dados recebidos correspondam à notação acima
using Interact sigmo(x,w,b) = 1 / (1 + exp(-w*x+b)) r_apples, g_apples, b_apples = apples[:, :red], apples[:, :green], apples[:, :blue] r_banans, g_banans, b_banans = banans[:, :red], banans[:, :green], banans[:, :blue]; @manipulate for w in 10:1:60, b in -5:1:25 plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(g_apples[1:5], zeros(10), label="Apple", colour = :red) scatter!(g_banans[1:5], ones(10), label="Banana", colour = :yellow) end
foon(x) = sigmo(x,60,24) plot(foon, 0, 1, label="Model", legend = :topleft, lw=3) scatter!(foon, g_apples, label="Apple", colour = :red) scatter!(foon, g_banans, label="Banana", colour = :yellow) xaxis!("green")
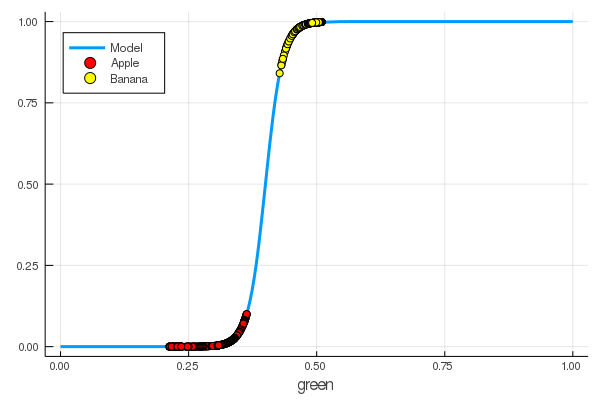
Ensinamos manualmente um neurônio para distinguir maçãs de bananas pela quantidade de verde!
Naturalmente, o desejo de automatizar esse processo. Introduzimos a função de perda
L(w,b)=(0−σ(x1,w,b))2+(1−σ(x2,w,b))2
Agora, o processo de aprendizado consistirá em minimizar esta função:
Código apples_mean_green = mean(g_apples) banans_mean_green = mean(g_banans) L(w, b) = (0 - sigmo(apples_mean_green,w,b))^2 + (1 - sigmo(banans_mean_green,w,b))^2 w_range = 10:0.5:30 b_range = 0:0.5:20 L_values = [L(w,b) for b in b_range, w in w_range] @manipulate for w in w_range, b in b_range p1 = surface(w_range, b_range, L_values, xlabel="b", ylabel="w", cam=(80,40), cbar=false, leg=false) scatter!(p1, [w], [b], [L(w,b)+1e-2], markersize=5, color = :blue) p2 = plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(p2, [apples_mean_green], [0.0], label="Apple", markersize=10) scatter!(p2, [banans_mean_green], [1.0], label="Banana", markersize=10, xlim=(0,1), ylim=(0,1)) plot(p1, p2, layout=(2,1)) end
Anteriormente, estudamos pacotes para Julia que permitem resolver problemas de otimização por vários métodos. Felizmente, o essencial já está no ambiente Flux!
Flux
using Flux
Primeiro, apresentamos os dados para treinamento de forma digerível:
Y = [zeros(length(g_apples)); ones(length(g_banans)) ] |> permutedims X = [g_apples; g_banans] |> permutedims;
Avançar na ordem:
- Criamos um conjunto de dados de treinamento combinando os dados de entrada com as respostas corretas em relação à classificação desses dados
- Definimos os parâmetros W e b por matrizes de valores aleatórios (há um sinal na entrada e um na saída, portanto, as matrizes têm tamanho 1 x 1 )
- Como modelo, definimos uma camada densa - um perceptron com uma função de ativação sigmoidal
- Definimos a função de perda - a soma das diferenças quadráticas (você ainda pode usar o
Flux.crossentropy() mais popular) - Como método de otimização, escolhemos a descida do gradiente . É preciso um parâmetro - a velocidade de descida
- Definimos uma função de avaliação que arredondará os valores das saídas do modelo e os comparará com as respostas corretas.
- E imprima os parâmetros do nosso modelo não treinado
dataz = [(X, Y)] W = param(rand(1)) b = param(rand(1)) model = Dense(W, b, σ) loss(x, y) = mse(model(x), y) opt = Descent(0.1) accuracy(x, y) = mean( round.(model(x)) .== y ) params(model) Params([[0.3372841444115968] (tracked), [0.8430399003786011] (tracked)])
Vamos ver qual é a saída da função de perda para nossos dados.
loss(X, Y)
E verifique os resultados da função de avaliação
accuracy(X, Y) 0.5
O resultado é bastante natural - as saídas são distribuídas de maneira bastante uniforme e metade dos dados é classificada corretamente:
Código modeldataz(x) = x |> model |> data |> permutedims
modelX = modeldataz(X) modelapples = modeldataz(g_apples') modelbanans = modeldataz(g_banans') plot(modelX, legend = false) hline!([0.5]) p1 = yaxis!((0,1)) curv = [-1:0.01:1;]' |> modeldataz plot( [-1:0.01:1;], curv, label="Model", legend = :topleft, lw=3) scatter!(g_apples, modelapples, label="Apple", colour = :red) scatter!(g_banans, modelbanans, label="Banana",colour = :yellow) hline!([0.5], lab = "", legend = :topleft) p2 = xaxis!("green") plot(p1, p2)
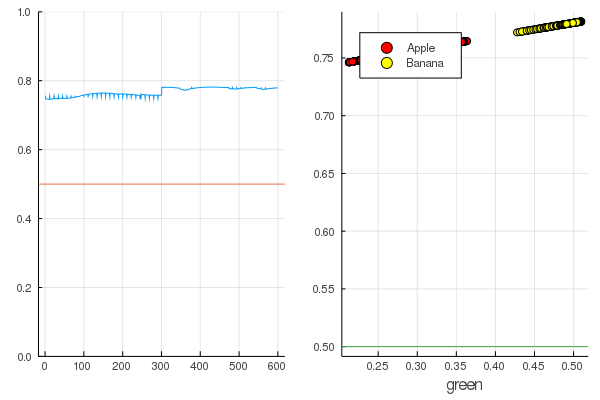
Vamos começar: é bem simples. Você só precisa gritar com a rede neural: “Treine!”, Enquanto indica no que treinar e no que minimizar, e ela concluirá uma sessão de treinamento. Portanto, forçaremos ela a desmamar tudo como deveria, mas apenas sem fanatismo, para que não haja reciclagem.
for i in 1:7000 train!(loss, params(model), dataz, opt) end model.W, model.b ([9.578663260720564] (tracked), [-3.7540362587506464] (tracked))
As perdas se tornaram muito menores:
loss(X, Y) 0.09152783090457564 (tracked)
Uma classificação é melhor:
accuracy(X, Y) 1.0
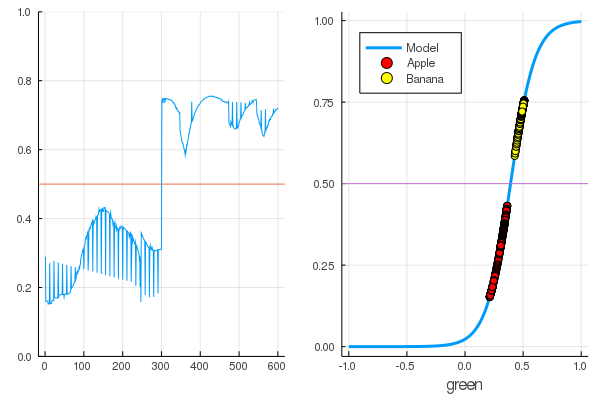
Os dados são divididos e mais treinamento tornará o modelo mais vertical. Verifique o modelo treinado no primeiro conjunto de frutas:
function classifier(img) gbimg = remove_background(img) greenmean = mean(float.(green.(gbimg))) answ = data( model( [ greenmean ]' ) )[1] fr = answ > 0.5 ? "Banana" : "Apple" "$fr $(round(200abs(0.5-answ)))%" end hcat(fruits...)

classifier.(fruits) 6-element Array{String,1}: "Apple 68.0%" "Apple 20.0%" "Banana 65.0%" "Banana 47.0%" "Banana 49.0%" "Banana 10.0%"
Uma maçã amarela especialmente plantada, é claro, não foi reconhecida corretamente e uma banana vermelha mal entrou em sua categoria. Mas o neurônio obtém apenas um número da imagem - a quantidade média de verde. Você pode adicionar outro sinal, digamos, a quantidade de azul, o que tornará o modelo um pouco mais adaptável.
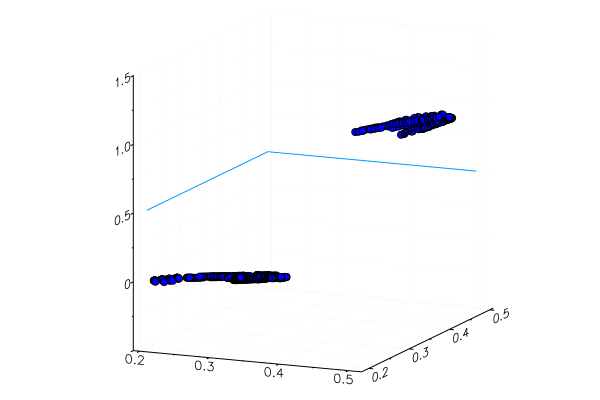
Ou você pode usar não a representação RGB, mas HSV (matiz, saturação, valor), na qual o canal de matiz conterá informações sobre a cor da imagem.
Todo o gosto pelas redes neurais é que elas próprias podem distinguir recursos que às vezes não são muito óbvios (correlação de cores, distribuição, contornos e curvas ...), e você pode ajudá-los com a ajuda de heurísticas e técnicas especiais, que transformam o trabalho com redes neurais em arte real.

Para que a liderança não cresça muito e fazer uma série de artigos com preguiça vamos também dar um exemplo da classificação de figuras com números escritos à mão, e o próprio leitor generalizará o conhecimento adquirido em imagens com frutas e criará sua própria rede neural, capaz de, por exemplo, marcar objetos em naturezas-mortas!
Mnist
using Images using Flux, Flux.Data.MNIST, Statistics using Flux: onehotbatch, onecold, crossentropy, throttle using Base.Iterators: repeated
Um exemplo é interessante porque já existem dez saídas. Os chamados vetores one-hot são úteis aqui.
labels = MNIST.labels()
10×60000 Flux.OneHotMatrix{Array{Flux.OneHotVector,1}}: 0 1 0 0 0 0 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 … 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0
Definimos uma cadeia de neurônios como um modelo, a entropia cruzada será uma função de perda e Adam como um método de otimização:
m = Chain( Dense(28^2, 32, relu), Dense(32, 10), softmax) loss(x, y) = crossentropy(m(x), y) accuracy(x, y) = mean(onecold(m(x)) .== onecold(y)) dataset = repeated((X, Y), 20) evalcb = () -> @show(loss(X, Y)) opt = ADAM()
Treine em um modo de economia, mas imprimindo perdas a cada 10 segundos:
for i = 1:10 Flux.train!(loss, params(m), dataset, opt, cb = throttle(evalcb, 10)) end
accuracy(X, Y) 0.64545
E verifique os dados não utilizados no treinamento
As redes neurais na Julia são simples e muito emocionantes! Mesmo que não seja necessário procurar conexões entre o seu campo de atividade e o aprendizado de máquina, você deve pelo menos sentir essa curiosidade, que é gritada de todos os ângulos, e não haverá escassez de ferramentas!
Todo o calor moderado da CPU!