Análise detalhada do método simplex

Prólogo

Recentemente, havia uma necessidade de criar um programa a partir do zero que implementasse o algoritmo do método simplex. Mas, no decorrer da solução, encontrei um problema: não há tantos recursos na Internet onde você pode analisar uma análise teórica detalhada do algoritmo (sua lógica: por que tomamos essas ou essas etapas) e dicas práticas de implementação - diretamente, o algoritmo. Então fiz uma promessa a mim mesma - assim que concluir a tarefa, escreverei meu post sobre esse tópico. Na verdade, falaremos sobre isso.

Observação. O post será escrito em uma linguagem bastante formal, mas será fornecido com comentários, o que deve trazer alguma clareza. Esse formato preservará a abordagem científica e, ao mesmo tempo, poderá ajudar alguns no estudo desta questão.

§1 Declaração do problema de programação linear

Definição: A programação linear é uma disciplina matemática dedicada à teoria e aos métodos de resolução de problemas extremos em conjuntos de espaço n-dimensional definidos por sistemas de equações e desigualdades lineares.

A tarefa geral da programação linear (doravante - LP) tem a forma:

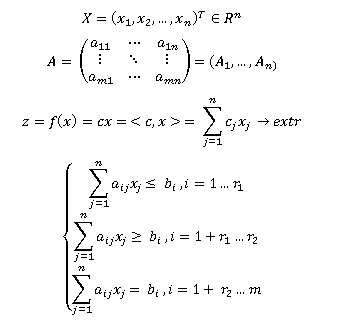
§2 A forma canônica do problema do LP

A forma canônica do problema do LP:



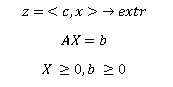Nota: Qualquer problema de LP é reduzido a canônico.

O algoritmo para a transição de um problema de LP arbitrário para a forma canônica:

1. Desigualdades com resultados negativos$$ $ inline $ b_i $ inline $ multiplique por (-1).
2. Se houver uma desigualdade na forma (≤), adicione ao lado esquerdo$$ $ inline $ s_i $ inline $ É uma variável adicional e obtemos igualdade.
3. Se houver uma desigualdade na forma (≥), subtraia do lado esquerdo$$ $ inline $ s_i $ inline $ , e obtemos a igualdade.
4. Fazemos a substituição de variáveis:

• Se$$ $ inline $ x_i ≤ 0 $ inline $ então$$ $ inline $ x_i '= -x_i ≥ 0 $ inline $
• Se$$ $ inline $ x_i $ inline $ - qualquer$$ $ inline $ x_i = x_i '- x_i' '$ inline $ onde$$ $ inline $ x_i ', x_i''≥ 0 $ inline $

Nota: Vamos numerar$$ $ inline $ s_i $ inline $ pelo número da desigualdade ao qual o adicionamos.

Nota:$$ $ inline $ s_i $ inline $ ≥0.

§3 Pontos de canto. Variáveis ​​básicas / livres. Soluções básicas

Definição: Point$$ $ inline $ X ∈ D $ inline $ chamado de ponto de canto se a representação$$ $ inline $ X = αX ^ 1 + (1-α) X ^ 2, onde X ^ 1, X ^ 2 ∈ D; 0 <α <1 $ inline $ só é possível com$$ $ inline $ X ^ 1 = X ^ 2 $ inline $ .

Em outras palavras, é impossível encontrar dois pontos na região, o intervalo de passagem que contém$$ $ inline $ X $ inline $ (ou seja,$$ $ inline $ X $ inline $ Não é um ponto interno).

O método gráfico para resolver o problema da PL mostra que encontrar a solução ideal está associada a um ponto de canto. Este é o conceito básico ao desenvolver um método simplex.

Definição: Haja um sistema de m equações e n incógnitas (m <n). Dividimos as variáveis ​​em dois conjuntos: (nm), definimos as variáveis ​​iguais a zero e as demais m variáveis ​​são determinadas pela resolução do sistema de equações iniciais. Se essa solução for única, m variáveis ​​diferentes de zero serão chamadas de básicas; variáveis ​​zero (nm) - livres (não básicas) e os correspondentes valores resultantes das variáveis ​​são chamados de solução básica.

§4 Método simplex

O método simplex permite que você encontre efetivamente a solução ideal, evitando a enumeração simples de todos os pontos de canto possíveis. O principal princípio do método: os cálculos começam com algum tipo de solução básica "inicial" e, em seguida, é feita uma busca por soluções que "melhorem" o valor da função objetivo. Isso é possível apenas se um aumento em alguma variável levar a um aumento no valor do funcional.

Pré-requisitos para a aplicação do método simplex:

1. A tarefa deve ter uma forma canônica.
2. A tarefa deve ter uma base explícita.

Definição: Uma base explicitamente selecionada é um vetor do formulário:$$ $ inline $ (.. 0100 ..) ^ T, (..010 ..) ^ T, (.. 0010 ..) ^ T ... $ inline $ , ou seja, apenas uma coordenada do vetor é diferente de zero e igual a 1.

Nota: O vetor base tem dimensão (m * 1), onde m é o número de equações no sistema de restrições.

Para maior conveniência dos cálculos e da visualização, geralmente são usadas tabelas simplex:

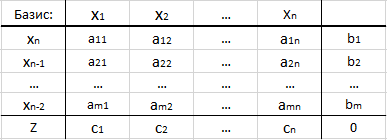
• A primeira linha indica o "nome" de todas as variáveis.
• Na primeira coluna, os números das variáveis ​​básicas são indicados e, na última célula, a letra Z (esta é a linha funcional).
• No "meio da tabela", indique os coeficientes da matriz de restrições - aij.
• A última coluna é o vetor do lado direito das equações correspondentes do sistema de restrições.
• A célula mais à direita é o valor da função objetivo. Na primeira iteração, é assumido como 0.

Nota: Base são variáveis, coeficientes na matriz de restrições nas quais formam vetores base.

Nota: Se as restrições no problema original são representadas por desigualdades da forma ≤, quando o problema é reduzido à forma canônica, as variáveis ​​adicionais introduzidas formam a solução básica inicial.

Nota: Os coeficientes na linha funcional são obtidos com o sinal “-”.

Algoritmo do método simplex:

1. Escolha uma variável que iremos introduzir na base. Isso é feito de acordo com o princípio indicado anteriormente: devemos escolher uma variável cujo aumento levará a um aumento no funcional. A seleção é feita de acordo com a seguinte regra:

• Se a tarefa estiver no mínimo, selecione o elemento positivo máximo na última linha.
• Se a tarefa estiver no máximo, selecione o mínimo negativo.

De fato, essa escolha corresponde ao princípio mencionado acima: se a tarefa é no mínimo, quanto maior o número que subtraímos, mais rápido o funcional diminui; para o máximo, pelo contrário - quanto maior o número, mais rápido o funcional cresce.

Nota: Embora levemos ao máximo o número negativo mínimo no problema, esse coeficiente mostra a direção do crescimento do funcional, pois a linha funcional na tabela simplex é obtida com o sinal “-”. Uma situação semelhante com minimização.

Definição: Uma coluna de uma tabela simplex correspondente a um coeficiente selecionado é chamada de coluna inicial .

2. Escolha uma variável que iremos introduzir na base. Para fazer isso, você precisa determinar quais variáveis ​​de base provavelmente desaparecerão quando a nova variável de base crescer. Algebricamente, isso é feito da seguinte maneira:

• O vetor das partes do lado direito é dividido pela coluna final
• Entre os valores obtidos, escolha o mínimo positivo (respostas negativas e zero não são consideradas)

Definição: Essa linha é chamada de linha principal e corresponde a uma variável a ser derivada da base.

Nota: De fato, expressamos as variáveis ​​de base antigas de cada equação do sistema de restrição através do restante das variáveis ​​e vemos em qual equação o aumento na nova variável de base provavelmente dará 0. Entrar nessa situação significa que "tropeçamos" em um novo vértice. É por isso que zero e elementos negativos não são considerados, porque Obter esse resultado significa que a escolha de uma nova variável de base nos afastará da área além da qual não há soluções.

3. Estamos procurando um elemento parado na interseção da linha e coluna principais.

Definição: Esse elemento é chamado de elemento principal .

4. Em vez da variável a ser excluída, na primeira coluna (com os nomes das variáveis ​​de base), escreva o nome da variável que inserimos na base.

5. Em seguida, inicia o processo de cálculo de uma nova solução básica. Ocorre usando o método Jordan-Gauss .

• Nova Linha de Lead = Linha de Leads Antiga / Lead
• Nova linha = Nova linha - Fator de linha na coluna principal * Nova linha principal

Nota: Uma conversão desse tipo visa introduzir a variável selecionada na base, ou seja, representação da coluna inicial como um vetor base.

6. Depois disso, verificamos a condição de otimização. Se a solução resultante não for ótima, repita todo o processo novamente.

§5 Interpretação do resultado do método simplex

1. Optimalidade

A condição de otimização para a solução resultante:

• Se a tarefa estiver no máximo, não haverá coeficientes negativos na linha funcional (ou seja, com qualquer alteração de variáveis, o valor da funcional resultante não aumentará).
• Se a tarefa é no mínimo, não há coeficientes positivos na linha funcional (ou seja, com qualquer alteração nas variáveis, o valor da funcional resultante não diminui).

2. Funcionalidade ilimitada

No entanto, vale a pena notar que um determinado funcional pode não atingir um máximo / mínimo em uma determinada área. O atributo algébrico disso pode ser formulado da seguinte maneira:

Ao escolher uma linha inicial (variável excluída), o resultado da divisão no sentido do vetor do lado direito pela coluna principal contém apenas valores zero e negativos.

De fato, isso significa que, não importa qual crescimento definimos uma nova variável base, nunca encontraremos um novo vértice. Portanto, nossa função não se limita ao conjunto de soluções viáveis.

3. Soluções alternativas

Ao encontrar a solução ideal, outra opção é possível - existem soluções alternativas (outro ponto de canto que fornece o mesmo valor do funcional).

Sinal algébrico da existência de uma alternativa:

Após alcançar a solução ideal, não há coeficientes para variáveis ​​livres na linha funcional.

Isso significa que, com o crescimento da variável correspondente com um coeficiente zero, o valor do funcional não será alterado e uma nova solução básica também fornecerá o ótimo do funcional.

Epílogo

Este artigo tem como objetivo uma compreensão mais profunda da parte teórica. Nos comentários e explicações aqui, você pode obter respostas para perguntas que geralmente são omitidas ao estudar esse método e tomadas a priori. No entanto, é preciso entender que muitos métodos de otimização numérica são baseados no método simplex (por exemplo, o método de Gomori , o método M ) e sem um entendimento fundamental, é improvável que muito progresso possa ser feito no estudo e na aplicação de todos os algoritmos dessa classe.

Um pouco mais tarde, escreverei um artigo sobre a implementação prática do método simplex, bem como vários artigos sobre o Método das Variáveis ​​Artificiais (Método M), o Método Gomori e o Método Branch and Border.

Obrigado pela atenção!

PS

Se você já está atormentado com a implementação do método simplex, aconselho a ler o livro de A. Taha. Introdução ao estudo das operações - tudo é bem analisado lá, tanto na teoria quanto nos exemplos; e também veja exemplos de solução de problemas do matburo.ru - isso ajudará na implementação do código.