Livro de Alan Turing e Nota Misteriosa - Detetive Científico

Tradução original no meu blog

Como esse livro chegou até mim?

Em maio de 2017, recebi um e-mail do meu antigo professor do ensino médio chamado George Rutter, no qual ele escreveu: “ Tenho uma cópia do grande livro alemão de Dirac (Die Prinzipien der Quantenmechanik), que pertenceu a Alan Turing e, posteriormente, enquanto eu lia seu livro Idea Makers , me parecia certo que você é a pessoa que precisa dele . " Ele me explicou que havia recebido um livro de outro (até então falecido) meu professor da escola Norman Rutledge , sobre quem eu sabia que ele era amigo de Alan Turing. George concluiu sua carta com a frase: " Se você precisar deste livro, eu poderia entregá-lo na próxima vez que você vier à Inglaterra ".

Depois de alguns anos em março de 2019, eu realmente cheguei à Inglaterra, depois do que concordei com George em me encontrar no café da manhã em um pequeno hotel em Oxford. Comemos, conversamos e esperamos a comida assentar. Então chegou o momento certo para discutir o livro. George colocou a mão na maleta e retirou um volume acadêmico típico, modestamente projetado, de meados do século XX.



Abri a capa, me perguntando se poderia estar no verso da inscrição: " Propriedade de Alan Turing" ou algo assim. Infelizmente, porém, não foi esse o caso. No entanto, uma nota suficientemente expressiva em quatro folhas de Norman Rutledge a George Rutter, escrita em 2002, foi anexada a ela.

Eu conhecia Norman Rutledge quando ainda era estudante do ensino médio em Eton no início dos anos 70. Ele era um professor de matemática apelidado de The Nutty Norman. Ele era um professor agradável em todos os aspectos e contou inúmeras histórias sobre matemática e todo tipo de outras coisas interessantes. Ele era responsável por garantir que a escola recebesse um computador (programado com uma fita perfurada da largura de uma mesa) - esse foi o primeiro computador que eu já havia usado .

Naquela época, eu não sabia nada sobre o passado de Norman (lembre-se de que isso foi muito antes do advento da Internet). Eu só sabia que ele era "Dr. Rutledge". Ele costumava contar histórias sobre pessoas de Cambridge, mas em suas histórias ele nunca mencionou Alan Turing. É claro que Turing não era famoso o suficiente na época (embora, como se saiba, eu já tenha ouvido falar dele por alguém que o conhecesse em Bletchley Park (a mansão em que o centro de criptografia estava localizado durante a Segunda Guerra Mundial)).

Alan Turing não era famoso até 1981, quando comecei a estudar programas simples , embora naquela época no contexto de autômatos celulares, e não em máquinas de Turing .

De repente, um dia, olhando para um catálogo de cartas na biblioteca do Instituto de Tecnologia da Califórnia , deparei-me com o livro Alan M. Turing , escrito por sua mãe Sarah Turing. O livro continha muitas informações, incluindo os trabalhos científicos não publicados de Turing sobre biologia. No entanto, eu não aprendi nada sobre seu relacionamento com Norman Rutledge, uma vez que o livro não mencionou nada sobre ele (embora, como eu descobri, Sarah Turing tenha correspondido a Norman sobre esse livro , e Norman até tenha escrito uma resenha no final).



Dez anos depois, sintonizado com extrema curiosidade por Turing e seu (então não publicado) trabalho de biologia , visitei o arquivo de Turing no King's College, em Cambridge . Logo, tendo me familiarizado com o que eles tinham do trabalho de Turing, e tendo passado algum tempo nisso, pensei que ao mesmo tempo poderia pedir que ele visse sua correspondência pessoal também. Examinando, encontrei várias cartas de Alan Turing a Norman Rutledge.

Naquela época, a biografia de Andrew Hodges foi publicada, o que fez tanto que Turing finalmente se tornou famoso, confirmou que Alan Turing e Norman Rutledge eram realmente amigos e também que Turing era consultor científico da Norman. Eu queria perguntar a Rutledge sobre Turing, mas nessa época Norman já estava aposentado e levava uma vida isolada. No entanto, quando concluí o trabalho no livro Um Novo Tipo de Ciência em 2002 (após meu retiro de dez anos), localizei-o e enviei a ele uma cópia do livro com a legenda "Para meu último professor de matemática". Então nos correspondemos um pouco e, em 2005, voltei à Inglaterra e aceitei me encontrar com Norman para tomar uma xícara de chá em um hotel de luxo no centro de Londres.

Tivemos uma boa conversa sobre muitas coisas, incluindo Alan Turing. Norman começou nossa conversa com a história de que ele realmente conhecia Turing, principalmente superficialmente, 50 anos atrás. Mas, no entanto, ele tinha algo a dizer sobre ele pessoalmente: " Ele não era sociável ". " Ele riu muito ." " Ele realmente não podia falar com os não matemáticos ". " Ele sempre teve medo de incomodar sua mãe ." " Ele saiu durante o dia e correu uma maratona ". " Ele não era muito ambicioso ." Então a conversa voltou à identidade de Norman. Ele disse que, apesar de já ter se aposentado há 16 anos, ele ainda escreve artigos para o " Mathematics Newspaper ", de modo que, em suas palavras, "para concluir todos os seus trabalhos científicos antes de ir para outro mundo " , onde, como ele acrescentou com um sorriso quase imperceptível, " todas as verdades matemáticas certamente serão reveladas ". Quando a festa do chá terminou, Norman vestiu a jaqueta de couro e se dirigiu ao ciclomotor, ignorando completamente as explosões que atrapalharam o tráfego em Londres naquele dia.

Foi a última vez que vi Norman, ele morreu em 2013.

Seis anos depois, sentei-me no café da manhã com George Rutter. Comigo estava uma nota de Rutledge, escrita por ele em 2002 em sua letra característica:



No começo, li a nota fluentemente. Ela era expressiva como sempre:

Recebi um livro de Alan Turing de seu amigo e executor Robin Gandy (no King's College, era normal distribuir livros da coleção de camaradas falecidos, e escolhi a coleção de poemas de A.E. Houseman dos livros de Ivor Ramsey como presente adequado (ele era o reitor e pulou da capela [em 1956]) ...

Mais tarde, em uma nota curta, ele escreve:

Você pergunta onde, no final, este livro deveria ter chegado - na minha opinião, deveria ir para alguém que aprecia tudo relacionado ao trabalho de Turing, para que seu destino dependa de você.

Stephen Wolfram me enviou seu livro impressionante, mas eu não mergulhei o suficiente nele ...

Concluindo, ele parabenizou George Rutter por ter tido a coragem de se mudar (como se viu, temporariamente) para a Austrália depois de se aposentar, dizendo que ele próprio " jogaria se mudando para o Sri Lanka como um exemplo de uma existência barata e de lótus ". mas acrescentou que "os eventos que acontecem lá agora indicam que ele não deveria ter feito isso " (aparentemente se referindo à guerra civil no Sri Lanka).

Então, o que está escondido nas entranhas do livro?

Então, o que fiz com uma cópia de um livro em alemão escrito por Paul Dirac que pertenceu a Alan Turing. Não leio alemão, mas tinha uma cópia do mesmo livro em inglês (que é o idioma do original) da edição de 1970. No entanto, uma vez no café da manhã, pareceu-me correto que eu revisasse cuidadosamente o livro página por página. No final, essa é uma prática comum ao lidar com livros antigos.

Note-se que fiquei impressionado com a elegância da apresentação de Dirac. O livro foi publicado em 1931, mas seu formalismo puro (e, sim, apesar da barreira da linguagem, eu conseguia ler a matemática descrita no livro) é quase o mesmo que se tivesse sido escrito hoje. (Não quero me concentrar muito em Dirac aqui, mas meu amigo Richard Feynman me disse que, pelo menos em sua opinião, a exposição de Dirac é monossilábica. Norman Rutledge me disse que ele era amigo em Cambridge do filho adotivo de Dirac , que se tornou um teórico em Norman costumava estar na casa de Dirac e disse que o “grande homem” às vezes desaparecia pessoalmente, enquanto o primeiro plano sempre apresentava muitos quebra-cabeças matemáticos.Infelizmente, eu nunca conheci Paul Dirac, embora Foi-me dito que depois de t uau, quando ele finalmente deixou Cambridge e foi para a Flórida, ele perdeu a maior parte de sua rigidez anterior e se tornou uma pessoa bastante sociável).

Mas voltando ao livro de Dirac, que pertencia a Turing. Na página 9, notei sublinhados e pequenas notas de margem escritas a lápis simples. Continuei a virar as páginas. Após vários capítulos, as notas desapareceram. Mas, de repente, encontrei uma nota incorporada na página 127 com o seguinte conteúdo:



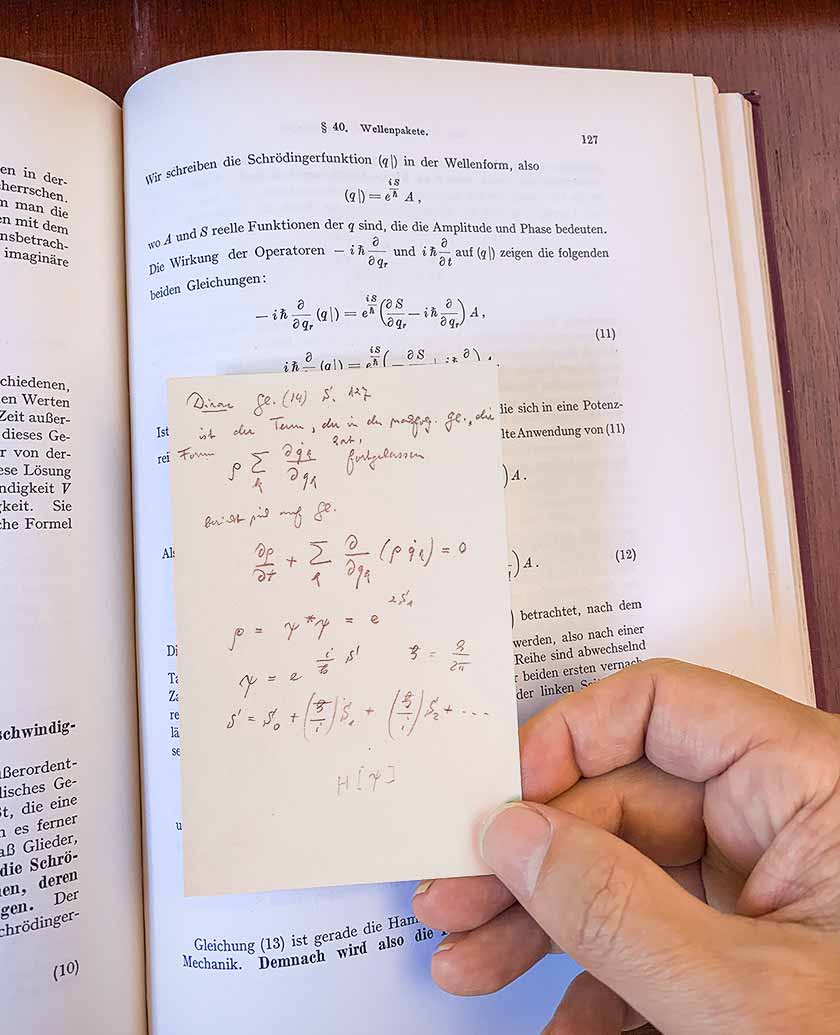
Foi escrito em alemão com caligrafia alemã padrão. E parece que de alguma forma poderia estar conectado com a mecânica lagrangiana . Eu pensei que provavelmente alguém possuía este livro antes de Turing, e essa deve ser uma nota escrita por essa pessoa.

Continuei folheando o livro. Sem anotações. E pensei que não poderia mais encontrar nada. Mas então, na página 231, encontrei o marcador da empresa - com texto impresso:



Acabarei encontrando mais alguma coisa? Continuei folheando o livro. Então, no final do livro, na página 259, na seção sobre a teoria relativística dos elétrons, encontrei o seguinte:



Desdobrei esta folha de papel:



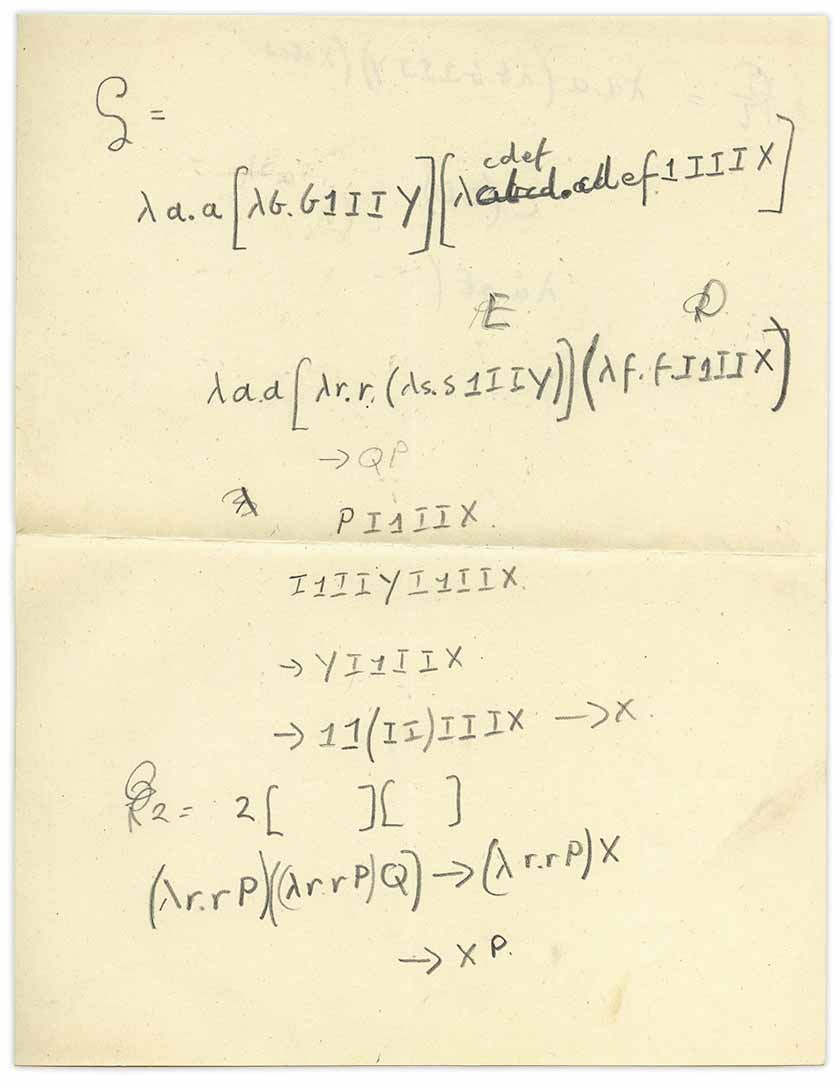
Percebi imediatamente que se tratava de um cálculo lambda com uma mistura de combinadores , mas como essa folha apareceu aqui? Lembre-se de que este livro é um livro sobre mecânica quântica, mas a folha em anexo trata da lógica matemática ou do que agora é chamado de teoria da computação. Isso é típico dos escritos de Turing. Gostaria de saber se Turing escreveu pessoalmente essa nota.

Mesmo durante o café da manhã, procurei na Internet as amostras de caligrafia de Turing, mas não encontrei exemplos na forma de cálculos, portanto não pude tirar conclusões sobre a identidade exata da caligrafia. E logo eu tive que ir. Empacotei cuidadosamente o livro, pronto para revelar o segredo do que era a página e quem o escreveu, e o levei comigo.

Sobre o livro

Primeiro de tudo, vamos discutir o livro em si. Os Princípios da Mecânica Quântica, de Paul Dirac, foram publicados em inglês em 1930 e logo foram traduzidos para o alemão. (O prefácio de Dirac é datado de 29 de maio de 1930; pertence ao tradutor Werner Bloch , em 15 de agosto de 1930.) O livro tornou-se um marco no desenvolvimento da mecânica quântica, estabelecendo sistematicamente um formalismo claro para a realização de cálculos e, entre outras coisas, explicando a previsão de Dirac sobre o pósitron , que será aberto em 1932.

Por que Alan Turing tinha um livro em alemão, não em inglês? Não sei ao certo, mas naqueles dias o alemão era a língua principal da ciência e sabemos que Alan Turing foi capaz de lê-lo. (Afinal, no título de sua famosa máquina de Turing , trabalho " Sobre números computáveis ​​com um apêndice ao problema de resolução (Entscheidungsproblem) ”era uma palavra alemã muito longa - e na parte principal do artigo ele opera com caracteres góticos bastante obscuros na forma de“ letras alemãs ”, que ele usou em vez de, por exemplo, caracteres gregos.

Alan Turing comprou o livro ou entregou a ele? Eu não sei No interior da capa do livro de Turing, há uma anotação a lápis “20 / -”, que era a notação padrão “20 xelins”, semelhante a £ 1. Na página direita, há um "26.9.30" apagado, supostamente significando 26 de setembro de 1930 - talvez a data em que o livro foi comprado pela primeira vez. Em seguida, no canto direito, o número apagado é "20". Talvez este seja novamente o preço. (Esse poderia ser o preço nos marcos do Reich , se assumirmos que o livro foi vendido na Alemanha? Naquela época, 1 Reichsmark valia cerca de 1 xelim, o preço alemão provavelmente seria escrito como, por exemplo, "20 RM".) Por fim, em a parte interna da contracapa é "c 5 / -" - talvez seja (com um grande desconto) o preço de um livro usado.

Vejamos as principais datas da vida de Alan Turing. Alan Turing nasceu em 23 de junho de 1912 (coincidentemente, exatamente 76 anos antes do Mathematica 1.0 ). No outono de 1931, ele entrou no King's College, em Cambridge. Ele recebeu seu diploma de bacharel após os três anos de estudo padrão, em 1934.

Na década de 1920 e início da década de 1930, a mecânica quântica era um assunto quente, e Alan Turing estava certamente interessado nela. Sabemos de seus arquivos que em 1932, assim que o livro foi publicado, ele recebeu os " Fundamentos Matemáticos da Mecânica Quântica " de John von Neumann (em alemão ). Também sabemos que em 1935 Turing recebeu uma tarefa do físico de Cambridge Ralph Fowler sobre o assunto do estudo da mecânica quântica. (Fowler propôs o cálculo da constante dielétrica da água , que na verdade é uma tarefa muito difícil, exigindo uma análise completa da teoria quântica de campos em interação, que ainda não está completamente resolvida).

E, no entanto, quando e como Turing conseguiu sua cópia do livro de Dirac? Dado que o livro tem um preço quebrado, Turing supostamente o comprou já usado. Quem foi o primeiro proprietário do livro? As notas no livro parecem relacionar-se principalmente à estrutura lógica, note-se que alguma relação lógica deve ser considerada um axioma. E a nota anexada na página 127?

Bem, isso pode ser uma coincidência, mas apenas na página 127 - Dirac fala sobre o princípio quântico da menor ação e estabelece as bases para uma integral ao longo do caminho de Feynman - que é a base de todo formalismo quântico moderno. O que a nota contém? Ele contém uma extensão da equação 14, que é uma equação para a evolução temporal da amplitude quântica. O autor da nota substituiu Dirac A por amplitude por ρ, possivelmente refletindo o registro alemão anterior (analogia da densidade do líquido). Em seguida, o autor tenta expandir a ação em potências de ℏ (a constante de Planck dividida por 2π, que às vezes é chamada de constante de Dirac ).

Mas parece que, pelo que está contido na página, há pouco que pode ser aprendido útil. Se você mantiver a página iluminada, ela conterá uma pequena surpresa - uma marca d'água com a inscrição "Z f. Physik. Chem. B ":



Esta é uma versão resumida do Zeitschrift für physikalische Chemie, Abteilung B , o periódico alemão de físico-química, publicado desde 1928. Talvez a nota tenha sido escrita pelo editor da revista? Aqui está o título da revista para 1933. Convenientemente, os editores são listados com sua localização e um deles se destaca: “Born · Cambridge”.



Este é Max Bourne, que é o autor da regra de Bourne e muito mais na teoria da mecânica quântica (assim como o avô da cantora Olivia Newton-John ). Então, esta nota pode ter sido escrita por Max Born? Infelizmente, porém, não é assim, porque a letra não corresponde.

E os marcadores da página 231? Aqui está de dois lados:



O marcador é estranho e muito bonito. Mas quando foi feito? Há uma livraria Heffers em Cambridge , embora agora faça parte da Blackwell. Por mais de 70 anos (até 1970), Heffers foi localizado no endereço, como mostra o marcador, 3 e 4 de Petty Cury .

Essa guia contém uma chave importante - este é o número de telefone „Tel. 862. " Aconteceu que em 1939 a maioria de Cambridge (incluindo Heffers) mudou para números de quatro dígitos e, é claro, em 1940 os marcadores foram impressos com números de telefone "modernos". (Os números de telefone em inglês aumentaram gradualmente; quando eu cresci na Inglaterra na década de 1960, nossos números eram Oxford 56186 e Kidmore End 2378. Em parte, eu me lembro desses números porque, curiosamente, agora é não parecia, eu sempre ligava para meu número ao atender uma chamada).

O marcador neste formulário foi impresso até 1939. Mas quanto tempo antes disso? Você pode encontrar algumas digitalizações de anúncios antigos da Heffers na Internet, pelo menos desde 1912 (junto com "Pedimos que você atenda às suas solicitações ..."), eles adicionam "Telefone 862" e "(2 linhas)". Também existem alguns indicadores com design semelhante que podem ser encontrados nos livros desde 1904 (embora não esteja claro se eles eram originais para esses livros (ou seja, impressos ao mesmo tempo) .Para os fins de nossa investigação, parece que podemos concluir que esse livro veio da loja Heffers (que, aliás, era a principal livraria de Cambridge) entre 1930 e 1939.

Página com cálculo lambda

Então agora sabemos algo sobre quando o livro foi comprado. Mas e a "página de cálculo lambda"? Quando isso foi escrito? Bem, é claro, até então, o cálculo lambda deveria ter sido inventado. E isso foi feito por Alonzo Church , um matemático de Princeton , em sua forma original em 1932 e em sua forma final em 1935. (Houve trabalhos de cientistas de seus antecessores, mas eles não usaram a notação λ).

Existe uma relação complexa entre Alan Turing e o cálculo lambda. Em 1935, Turing se interessou pela “mecanização” das operações matemáticas e inventou a idéia de uma máquina de Turing usá-la para resolver os problemas dos fundamentos da matemática. Turing enviou um artigo sobre esse assunto à revista francesa ( Comptes rendus ), mas foi perdido pelo correio; e então descobriu-se que o destinatário a quem ele a enviou ainda não estava lá, desde que ele havia mudado a China.

Mas em maio de 1936, mesmo antes de Turing poder enviar seu artigo para outro lugar, o trabalho da Igreja Alonzo chegou dos Estados Unidos . , 1934 , , , 1922 .
, - , ( - ). ( ) , , . 1936 ( ) « …» .

: 1936 1938 ( 1937 ) , , . , -, — , - , — , , .

1938 , , -, , . 1945 , . 1947–8 , , .

1951 . ( , , , , - , ). , 1954 , : « » ( : « , »). , , 7 1954 , . ( , , .)

, -. , :



, , , . ? , , , Spalding&Hodge, Papermakers, « », - , -, . , , , Excelsior, , 1890- 1954 .

?

Então, vamos dar uma olhada no que está nos dois lados da folha. Vamos começar com lambdas.

Aqui está uma maneira de definir funções "puras" ou "anônimas" , e elas são o conceito básico em lógica matemática e agora em programação funcional. Essas funções são bastante comuns na Wolfram Language , e seu trabalho é bem fácil de explicar. Por exemplo, alguém escreve f [ x ] para denotar a função f aplicada ao argumento x. E existem muitas funções nomeadas como Abs ou Sin ou Blur . Mas e se alguém quiser que f [ x ] seja 2x +1 ? Não há nome imediato para esta função. Mas existe outra forma de atribuição, f [ x ]?

A resposta é sim: em vez de f , escrevemos a Function[a,2a+1] . E na linguagem das Function [a,2a+1][x] Wolfram Function [a,2a+1][x] aplica funções ao argumento x, produzindo 2x+1 como resultado. Function[a,2a+1] é uma função “pura” ou “anônima”, que é uma operação pura de multiplicar por 2 e adicionar 1.

Portanto, λ no cálculo lambda é um análogo exato da Função na Língua Wolfram - e, portanto, por exemplo, λ a. (2 a + 1) é equivalente à Function[a, 2a + 1] . (Vale ressaltar que a função, digamos, Function[b,2b+1] equivalente; as "variáveis ​​relacionadas" a ou b são apenas lugares para substituir o argumento da função - e na Wolfram Language elas podem ser evitadas usando opções alternativas para definir uma função pura (2# +1)& ).

Na matemática tradicional, as funções são geralmente consideradas como objetos que exibem dados de entrada (por exemplo, números inteiros) e dados de saída (que também são, por exemplo, números inteiros). Mas o que é esse objeto Function (ou λ)? Em essência, este é um operador estrutural que pega expressões e as transforma em funções. Isso pode parecer um pouco estranho em termos da matemática tradicional e da forma matemática da escrita, mas se alguém precisar manipular caracteres arbitrários, o que é muito mais natural, mesmo que a princípio pareça um pouco abstrato. (Note-se que, quando os usuários aprendem a Wolfram Language, posso sempre dizer que eles superaram um certo limiar de pensamento abstrato quando obtêm uma idéia da Função ).

Lambdas são apenas parte do que está na página. Existe outro conceito, ainda mais abstrato - esses são combinadores . Considere a linha PI1IIx bastante obscura? O que isso significa? De fato, esta é uma sequência de combinadores ou alguma composição abstrata de funções simbólicas.

A superposição usual de funções, bastante familiar em matemática, na Wolfram Language pode ser escrita na forma: f[g[x]] - que significa "aplicar f ao resultado da aplicação de g em x ". Mas os suportes são realmente necessários para isso? Em Wolfram, f@g@ x é uma forma alternativa de notação. Nesta publicação, contamos com a definição da Wolfram Language: o operador @ está associado ao lado direito, então f@g@x equivalente a f@(g@x) .

Mas o que a entrada (f@g)@x significa? Isso é equivalente a f[g][x] . E se f e g fossem funções comuns em matemática, isso seria inútil, mas se f é uma função de ordem superior , então f[g] si pode ser uma função que pode muito bem ser aplicada a x .

Observe aqui que ainda há alguma complexidade. Em f[] - f é uma função de um argumento. E f[] equivalente a escrever a Function[a, f[a]][x] . Mas e a função de dois argumentos, digamos, f[x,y] ? Isso pode ser escrito como Function[{a,b},f[a, b]][x, y] . Mas e a Function[{a},f[a,b]] ? O que é isso Existe uma "variável livre" b , que é simplesmente passada para a função. Function[{b},Function[{a},f[a,b]]] vincularão essa variável e, em seguida, a Function[{b},Function[{a},f [a, b]]][y][x] fornece f[x,y] novamente. (Definir a função para que ele tenha um argumento é chamado de "currying" em homenagem ao cientista lógico chamado Haskell Curry ).

Se existirem variáveis ​​livres, ou seja, existem muitas dificuldades diferentes em relação à forma como as funções podem ser definidas, mas se nos restringirmos a objetos Function ou λ que não possuem variáveis ​​livres, eles poderão ser configurados livremente. Tais objetos são chamados combinadores.

Os combinadores têm uma longa história. Sabe-se que elas foram propostas pela primeira vez em 1920 pelo discípulo de David Gilbert , Moses Schoenfinkel .

Naquela época, apenas muito recentemente foi descoberto que você não precisava usar as expressões And , Or e Not para representar expressões na lógica proposicional padrão: bastava usar o único operador, que agora chamaremos Nand (porque, por exemplo, se escrevermos Nand como ·, Então Or[a,b] assume a forma (a · a) · (b · b) ). Schönfinkel queria encontrar a mesma representação mínima da lógica de predicados, ou essencialmente lógica, incluindo funções.

Ele criou dois "combinadores" S e K. Na Wolfram Language, isso é escrito como
K [x _] [y_] → xe S [x _] [y _] [z_] → x [z] [y [z]].

Vale ressaltar que foi possível usar esses dois combinadores para realizar quaisquer cálculos. Então por exemplo

S [K [S]] [S [K [S [K [S]]]] [S [K [K]]]]

pode ser usado como uma função para adicionar dois números inteiros.

Tudo isso, para dizer o mínimo, são objetos bastante abstratos, mas agora que entendemos o que são as máquinas de Turing e o cálculo lambda, podemos ver que os combinadores de Schoenfinkel realmente anteciparam o conceito de computação universal. (E ainda mais notável, as definições de S e K de 1920 são minimamente simples e se assemelham à muito simples máquina universal de Turing que propus nos anos 90, cuja universalidade foi comprovada em 2007 ).

Mas voltando ao nosso folheto e linha PI1IIx . Os caracteres registrados aqui são combinadores e todos são projetados para definir uma função. Aqui a definição é que a superposição de funções deve ser associativa à esquerda, de modo que fgx não deve ser interpretado como f @ g @ x ou f @ (g @ x) ou f [g [x]], mas sim como (f @ g ) @x ou f [g] [x]. Traduziremos esta entrada para um formato conveniente para o Wolfram Language: o PI1IIx assumirá o formato p [i] [one] [i] [i] [x] .

Por que escrever algo assim? Para explicar isso, precisamos discutir o conceito de número de igrejas (em homenagem a Alonzo Church). Digamos que apenas trabalhamos com símbolos e com lambdas ou combinadores. Existe uma maneira de usá-los para especificar números inteiros?

Que tal dizer apenas que o número n corresponde à Function[x, Nest[f,x,n]] ? Ou, em outras palavras, que (em notação mais curta):

1 é f[#]&
2 é f[f[#]]&
3 é f[f[f[#]]]& e assim por diante.

Tudo isso pode parecer um pouco mais obscuro, mas o motivo pelo qual é interessante é que nos permite fazer tudo completamente simbólico e abstrato, sem ter que falar explicitamente sobre algo como números inteiros.

Com esse método de especificação de números, imagine, por exemplo, adicionar dois números: 3 podem ser representados como f[f[f[#]]]& e 2 é f[f[#]]& . Você pode adicioná-los simplesmente aplicando um deles ao outro:



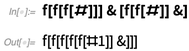
Mas como é f ? Poderia ser qualquer coisa! De certo modo, "vá para lambda" até o fim e represente números usando funções que aceitam f como argumento. Em outras palavras, imagine 3, por exemplo, como Function[f,f[f[f[#]]] &] ou Function[f,Function[x,f[f[f[x]]]] . (quando e como você precisa nomear variáveis ​​é um problema no cálculo lambda).

Considere um fragmento do artigo de Turing de 1937, Computability e λ-Diffusibility , que configura objetos exatamente como acabamos de discutir:



Aqui, a gravação pode ser um pouco confusa. O x de Turing é nosso f , e seu x ' (o compositor cometeu um erro ao inserir um espaço) é nosso x . Mas aqui é usada exatamente a mesma abordagem.

Então, vamos olhar para a linha imediatamente após a dobra em frente à folha. Isso é I1IIYI1IIx . De acordo com a forma da Wolfram Language, este será i[one][i][i][y][i][one][i][i][x] . Mas aqui eu sou uma função idêntica, portanto i[one] retorna apenas um . Enquanto isso, uma é a representação numérica da Igreja para 1 ou Function[f,f[#]&] . Mas com esta definição, one[] se torna a[#]& e one[a][b] se torna a[b] . (A propósito, i[][b] ou Identity[][b] também são a [b] ).

Será muito mais claro se escrevermos as regras de substituição para ie uma , em vez de usar diretamente o cálculo lambda. O resultado será o mesmo. Aplique essas regras explicitamente, obtemos:



E é exatamente igual ao apresentado no primeiro registro abreviado:



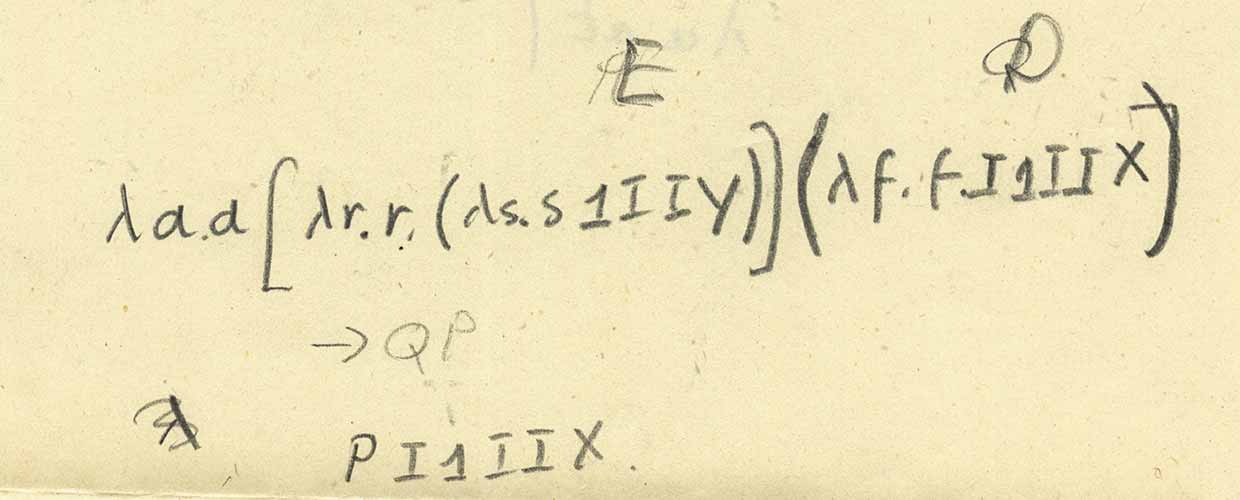
Vamos agora olhar para a folha novamente, no topo:



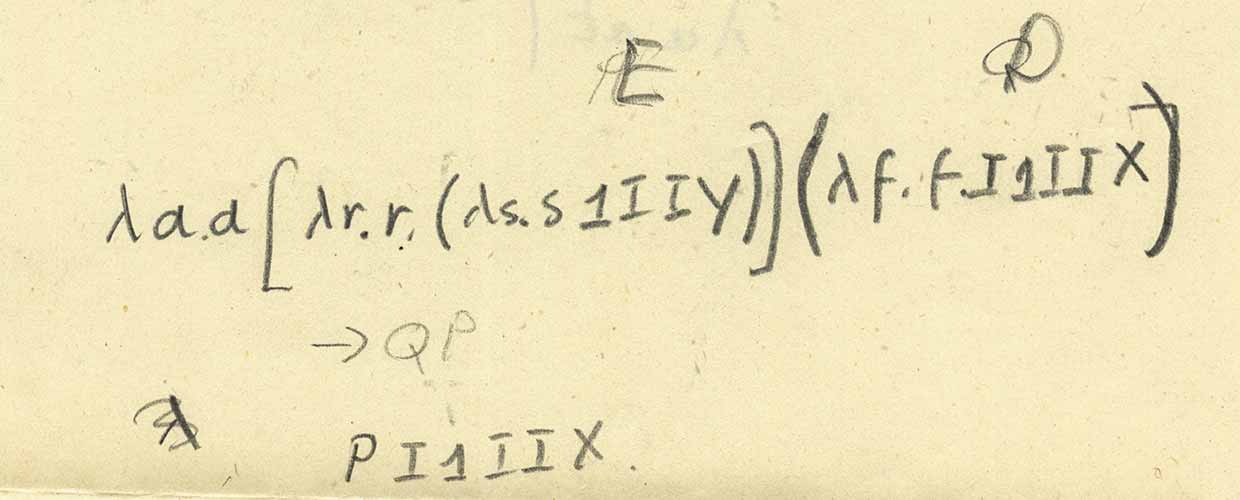
Existem objetos bastante confusos e incompreensíveis “E” e “D”, mas por eles queremos dizer “P” e “Q”, para que possamos escrever a expressão e calculá-la (observe que aqui - depois de alguma confusão com a última símbolo - "cientista misterioso" coloca [...] e (...) para representar as funções de aplicação):



Portanto, esta é a primeira abreviação mostrada. Para ver mais, vamos substituir definições para Q:



Temos exatamente a seguinte abreviação mostrada. O que acontece se substituirmos as expressões por P?



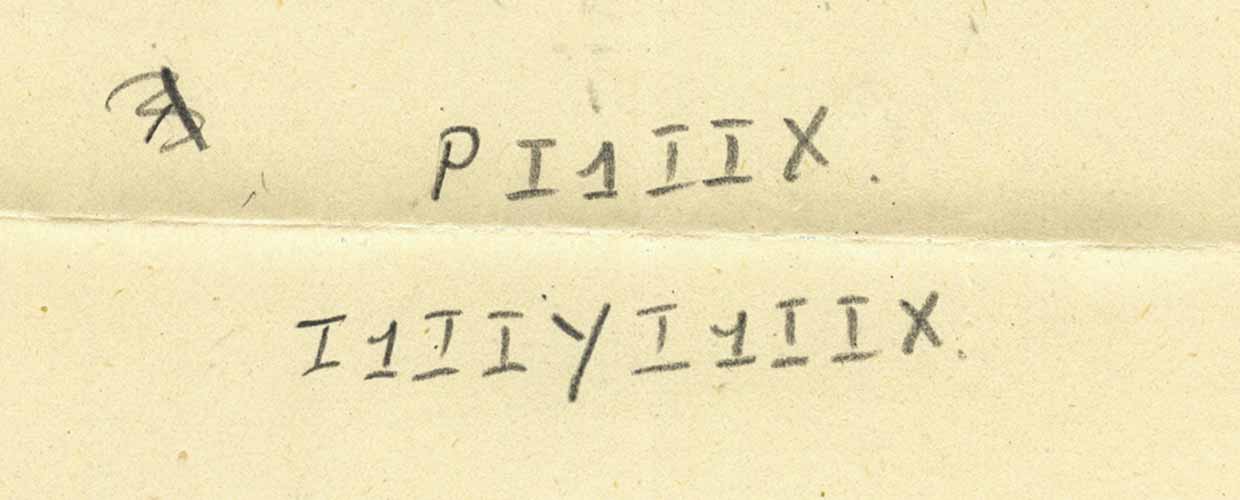
Aqui está o resultado:



E agora, usando o fato de que i é uma função que gera o próprio argumento, obtemos:



Oooops! Mas essa não é a próxima linha gravada. Há algum erro aqui? Não está claro. Porque, no final, diferentemente da maioria dos outros casos, não há seta indicando que a próxima linha segue a anterior.

Aqui está algum tipo de mistério, mas vamos para a parte inferior do folheto:



Aqui 2 é o número da Igreja, definido, por exemplo, pelo padrão two[a_] [b_] → a[a[b]] . Observe que esta é realmente a forma da segunda linha se a for tratado como Function[r,r[]] eb como q . Portanto, esperamos que o resultado dos cálculos seja o seguinte:



No entanto, a expressão [b] dentro dela pode ser escrita como x (provavelmente difere de x anteriormente escrito na folha) - como resultado, obtemos o resultado final:



Portanto, podemos decifrar um pouco do que está acontecendo nesta folha, mas pelo menos um enigma que ainda permanece é o que Y deveria ser.

De fato, a lógica combinatória possui um combinador Y padrão: o chamado combinador de ponto fixo . Formalmente, é definido pelo fato de que Y [ f ] deve ser igual a f [Y [ f ]], ou, em outras palavras, Y [ f ] não muda quando f é aplicado, portanto esse é um ponto fixo para f . (O combinador Y está associado ao número 0 na linguagem Wolfram.)

Atualmente, o Y-combinator se tornou famoso graças ao acelerador de lançamento Y-Combinator , chamado Paul Graham (que por muito tempo era fã de programação funcional e da linguagem de programação LISP e implementou a primeira loja on-line com base nessa linguagem). Uma vez ele me disse pessoalmente: " ninguém entende o que Y é um combinador ". (Note-se que o Y Combinator é exatamente o que permite às empresas evitar operações de ponto fixo ...)

O combinador Y (como um combinador de ponto fixo) foi inventado várias vezes. Turing realmente veio com sua implementação em 1937, que ele chamou de Θ. Mas a letra “Y” em nossa página é um famoso combinador de ponto fixo? Talvez não. Então, qual é o nosso "Y"? Considere esta redução:



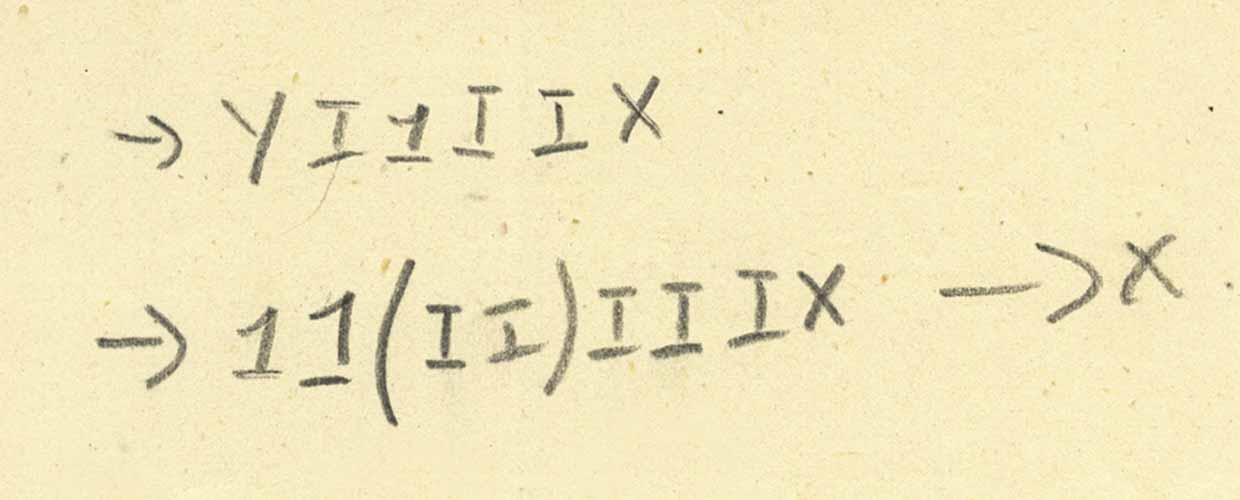
Mas essas informações claramente não são suficientes para determinar inequivocamente o que Y é. É claro que Y opera não apenas com um argumento; parece que o assunto é de pelo menos dois argumentos, mas não está claro (pelo menos para mim) quantos argumentos são necessários para entrada e o que ele faz.

Finalmente, embora possamos entender muitas partes do folheto, devemos dizer que, em escala global, não está claro o que foi feito nele. Embora exija muitas explicações sobre o que é apresentado na planilha, é bastante elementar no cálculo lambda e no uso de combinadores.

Presumivelmente, aqui está uma tentativa de criar um "programa" simples - usando cálculo e combinadores lambda para fazer algo. Mas, na medida em que isso é típico da engenharia reversa, é difícil dizer o que esse "algo" deve ser e qual é o objetivo comum "explicável".

Há outro recurso apresentado na folha, que vale a pena comentar aqui - é o uso de vários tipos de colchetes. Na matemática tradicional, os parênteses são usados ​​principalmente para tudo - e aplicações de uma função (como em f (x) ) e agrupamentos de membros (como em (1 + x) (1-x) , ou, menos obviamente, um (1- x) ). (Na Wolfram Language, separamos os vários usos de colchetes - entre colchetes para definir funções f [x] - e parênteses são usados ​​apenas para agrupamento).

Quando o cálculo lambda apareceu pela primeira vez, havia muitas perguntas sobre o uso de colchetes. Mais tarde, Alan Turing escreveu um trabalho inteiro (não publicado) intitulado " Transformando a forma matemática da notação e fraseologia ", mas já em 1937 ele achava que precisava descrever definições modernas (um tanto hackers) para o cálculo lambda (que, aliás, apareciam em para a Igreja).

Ele disse que f aplicado a g deve ser escrito {f} (g) , a menos que f seja o único caractere; nesse caso, poderia ser f (g) . Ele então disse que lambda (como na Function[a, b] ) deve ser escrita como λ a [ b ] ou, alternativamente, λ a . b .

No entanto, talvez em 1940 toda a idéia de usar {...} e [...] para denotar objetos diferentes tenha sido descartada, principalmente em favor de colchetes em um estilo matemático padrão.

Dê uma olhada no topo da página:



Nesta forma, é difícil de entender. Nas definições da Igreja, os colchetes são para agrupamento, com um colchete de abertura que substitui um ponto. Usando essa definição, fica claro que Q (eventualmente rotulado como D), entre parênteses no final, é o que todo o lambda inicial se aplica.

De fato, o colchete aqui não limita o corpo da lambda; em vez disso, na verdade, representa outra aplicação da função e não há indicação explícita de onde o corpo lambda termina. No final, pode-se ver que o “cientista misterioso” mudou o colchete de fechamento para um redondo, aplicando efetivamente a definição de Church - e forçando-o a calcular a expressão, como mostrado na folha.

Então, o que esse pequeno pedaço significa mesmo assim? Acho que isso sugere que a página foi escrita na década de 1930, ou não muito tempo depois, já que a lenda dos colchetes ainda não havia se estabelecido.

Então, de quem era a letra?

Então, antes disso, conversamos sobre o que está escrito na página. Mas e quem escreveu a mesma coisa?

O candidato mais óbvio para esse papel seria o próprio Alan Turing, pois, afinal, a página estava dentro de seu livro. Em termos de conteúdo, parece que não há nada incompatível com o fato de Alan Turing poder escrever isso - mesmo no momento em que começou a lidar com o cálculo lambda depois de receber o artigo de Church no início de 1936.

Que tal caligrafia? Pertence a Alan Turing? Considere várias amostras sobreviventes, que, como sabemos com certeza, foram escritas por Alan Turing:



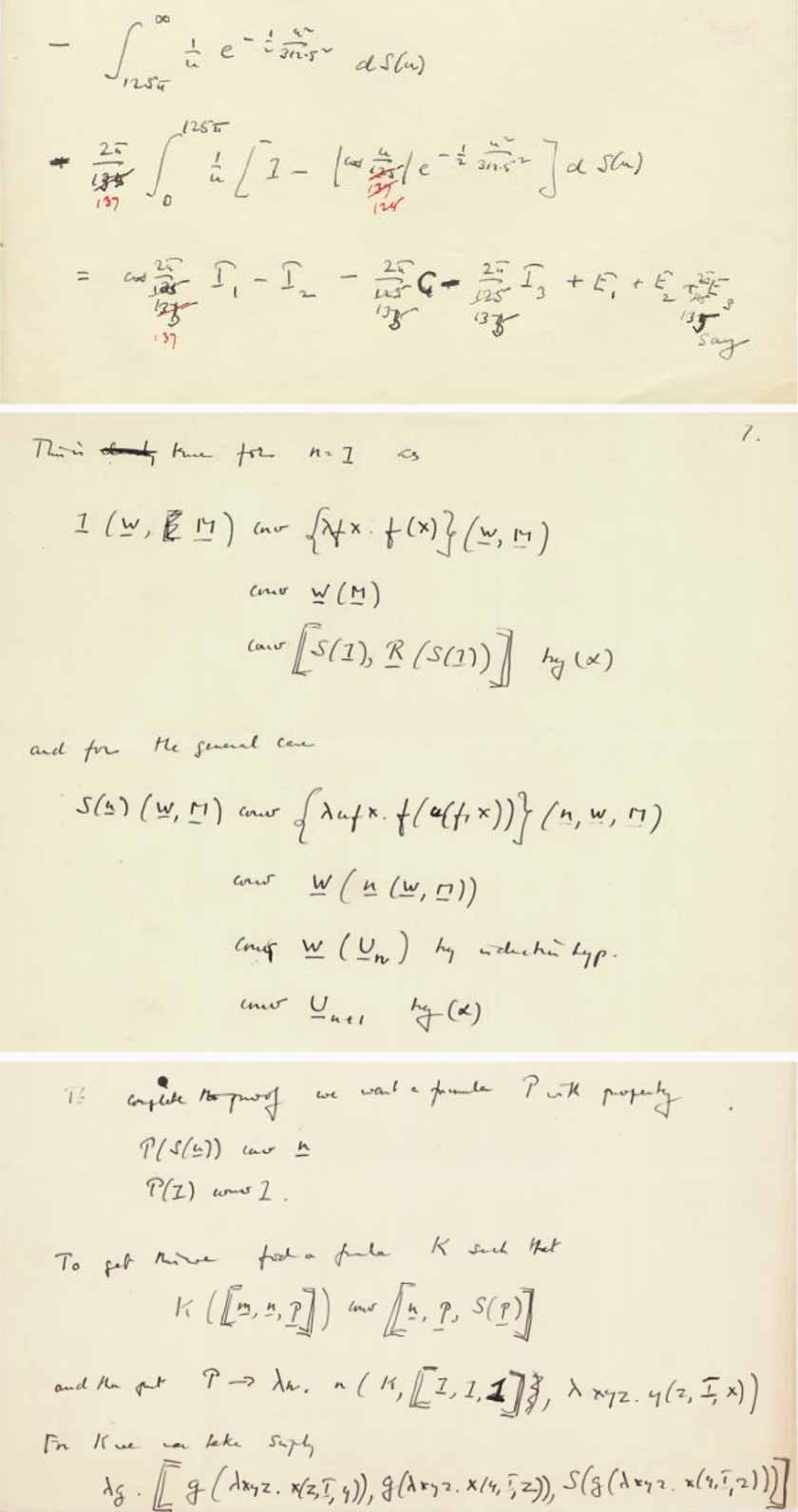
O texto apresentado parece claramente muito diferente, mas e a notação usada no texto? Pelo menos, na minha opinião, isso não parece tão óbvio - e pode-se supor que qualquer diferença possa ser causada pelo fato de as amostras existentes (apresentadas nos arquivos) serem escritas, por assim dizer, "no final", enquanto as nossas uma página é um reflexo do trabalho do pensamento.

Tornou-se conveniente para nossa investigação que houvesse uma página no arquivo Turing na qual ele escrevesse uma tabela de caracteres necessários para a notação. E, ao comparar esses caracteres letra por letra, eles se parecem muito comigo (esses registros foram feitos durante o tempo de Turing, quando ele estudava o crescimento das plantas , daí a notação "área foliar"):



Como eu queria investigar isso mais profundamente, enviei amostras para Sheila Lowe , uma especialista em caligrafia profissional (e autor de caligrafia), que conheci uma vez - apenas apresentando nossa planilha como "amostra A" e a caligrafia existente de Turing como "Amostra" B ". Sua resposta foi final e negativa: “ O estilo de escrever é completamente diferente. Quanto à personalidade, o autor da amostra "B" tem uma maneira de pensar mais rápida e intuitiva do que o autor da amostra "A ". "

Ainda não estava completamente convencido disso, mas decidi que era hora de procurar outras opções.

Então, se Turing não escreveu isso, quem o fez? Norman Rutledge me disse que recebeu o livro de Robin Gandhi, que era o executor de Turing. Então enviei "Sample" C "" de Gandhi:



Mas a conclusão inicial de Sheila foi que as três amostras foram provavelmente escritas por três pessoas diferentes, observando novamente que a amostra "B" foi obtida do " pensador mais rápido - aquele que provavelmente está mais disposto a procurar soluções incomuns para os problemas " . (Acho agradável que um especialista em caligrafia moderna faça uma avaliação da caligrafia de Turing, tendo em conta o quão ativamente todos nas tarefas escolares de Turing da década de 1920 se queixavam de sua caligrafia).

Bem, naquele momento, parecia que Turing e Gandhi foram excluídos da lista de "suspeitos". Então, quem poderia escrever isso? Comecei a pensar em pessoas para quem Turing poderia emprestar seu livro. Obviamente, ao mesmo tempo, eles devem poder fazer cálculos usando o cálculo lambda.

Sugeri que a pessoa fosse de Cambridge, ou pelo menos da Inglaterra, dada a marca d'água no papel. Confundi a hipótese de trabalho de que mais ou menos 1936 era o momento certo para escrever isso. Então, quem ele conhecia naquela época e com quem Turing se comunicava? . ( 13 , 1930 1936 .)

. , , , — 1933 , («» ) : 0.12345678910111213… ( 1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, , «» , ).

1937 - , , . ( , - ).

, ( ) , . ( , 1948 Turbochamp — , , ).

? LinkedIn, , , Microsoft. , , . ( ):



, ( f . .)

? , . « », , . ( , , , , , ).

— , .

«»

, . , , , , , .

, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .

? - (, , , 2005 , «»). , « ».

- , , , ? . , - - - . , 1955 « » ( , BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .

. , , , « ». , , , , 1954 , . , , .

, « ( , ) » « , , , , [ ] ». , ? . ( , , , 1902 , « » : « »).

, , , , , 12 , -, , , 21 ).

, , - . , - . , , , 1938 . 2000 - ( ) — , , 2002 , .

, , ? , , . :



, . , , , , , .

: ? , , , .

- , — 1940 — . , 1944 , , . , , .

, , , , 1952 , « » . , , , , — , , . , . , , , , . , 1980- , “ » — , , , . ( , , , , « , »). , « , , , — … », , « ».)

, , . . , « » (. . -), -.

. 1969 , , , , , .
, , . . — — . . - , , .

1995 , . — . . , , — , , , . , , , , , 24 . ( 2001 — 45 ).

, ? , , , , , ( , , , c ). ( ) « » ( ), , -, , . , .

, . , 30 , . , , , - — , , , (, , , Mathematica ). , , , , , , , . , , , .

? , , () , . ( , .) , 1 . , .

, , . : « ! » , . . , -, , , .

, , , , , . , : . ; .

, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.

, - , , , . , , , , , , . , , — , , …

: ( ), ( ) ( ).

Wolfram Language?
.
Inscrição para novos cursos . Curso online pronto.
Wolfram Language.