Resolva a equação de regressão linear simples

O artigo discute vários métodos para determinar a equação matemática de uma linha de regressão simples (em pares).

Todos os métodos para resolver a equação discutida aqui são baseados no método dos mínimos quadrados. Denotamos os métodos da seguinte maneira:

• Solução analítica
• Descida de gradiente
• Descida do gradiente estocástico

Para cada um dos métodos para resolver a equação da linha reta, o artigo descreve várias funções divididas principalmente nas que são escritas sem o uso da biblioteca NumPy e naquelas que usam o NumPy para cálculos. Acredita-se que o uso hábil do NumPy reduza os custos de computação.

Todo o código deste artigo está escrito em python 2.7 usando o Jupyter Notebook . Código-fonte e arquivo de dados de amostra postado no github

O artigo é mais voltado para iniciantes e para aqueles que já começaram a dominar o estudo de uma seção muito extensa de inteligência artificial - aprendizado de máquina.

Para ilustrar o material, usamos um exemplo muito simples.

Condições de exemplo

Temos cinco valores que caracterizam a dependência de Y em X (Tabela No. 1):

Tabela No. 1 "Condições do exemplo"



Assumimos que os valores $$$x_i$ É o mês do ano e $$$y_i$ - receita este mês. Em outras palavras, a receita depende do mês do ano e $$$x_i$ - o único sinal de que depende a receita.

Um exemplo é mais ou menos isso, tanto em termos da dependência condicional da receita em relação ao mês do ano, quanto em termos de número de valores - existem muito poucos deles. No entanto, essa simplificação permitirá que o que é chamado nos dedos explique, nem sempre com facilidade, o material absorvido pelos iniciantes. E também a simplicidade dos números permitirá, sem custos trabalhistas significativos, aqueles que desejam resolver o exemplo no papel.

Suponha que a dependência mostrada no exemplo possa ser bastante bem aproximada pela equação matemática de uma linha de regressão simples (em pares) da forma:

$$

$$Y = a + bx$$

onde $$$x$ - este é o mês em que a receita foi recebida, $$$Y$ - receita correspondente ao mês, $$$a$ e $$$b$ - coeficientes de regressão da linha estimada.

Observe que o coeficiente $$$b$ freqüentemente chamado de declive ou gradiente da linha estimada; representa a quantidade pela qual alterar $$$Y$ quando mudar $$$x$ .

Obviamente, nossa tarefa no exemplo é selecionar esses coeficientes na equação $$$a$ e $$$b$ para os quais os desvios de nossa receita mensal estimada em relação às respostas verdadeiras, ou seja, Os valores apresentados na amostra serão mínimos.

Método dos mínimos quadrados

De acordo com o método dos mínimos quadrados, o desvio deve ser calculado ao quadrado. Tal técnica evita o pagamento mútuo de desvios, se eles tiverem sinais opostos. Por exemplo, se em um caso, o desvio for +5 (mais cinco) e no outro -5 (menos cinco), a soma dos desvios será paga mutuamente e será 0 (zero). Você não pode desperdiçar o desvio, mas use a propriedade module e todos os desvios serão positivos e se acumularão em nós. Não vamos nos aprofundar neste ponto em detalhes, mas simplesmente indicar que, para a conveniência dos cálculos, é habitual calcular o desvio.

É assim que a fórmula se parece com a ajuda da qual determinamos a menor soma dos desvios ao quadrado (erros):

$$

$$ERR (x) = \ soma \ limites_ {i = 1} ^ n (a + bx_i - y_i) ^ 2 = \ soma \ limites_ {i = 1} ^ n (f (x_i) -y_i) ^ 2 \ rightarrow min$$

onde $$$f (x_i) = a + bx_i$ É uma função da aproximação de respostas verdadeiras (ou seja, receita calculada por nós),

$$$y_i$ - estas são respostas verdadeiras (receita fornecida na amostra),

$$$i$ É o índice da amostra (o número do mês em que o desvio é determinado)

Diferenciamos a função, definimos as equações diferenciais parciais e estamos prontos para prosseguir para a solução analítica. Mas primeiro, vamos fazer uma breve digressão sobre o que é diferenciação e relembrar o significado geométrico da derivada.

Diferenciação

Diferenciação é a operação de encontrar a derivada de uma função.

Para que serve um derivado? A derivada de uma função caracteriza a taxa de alteração de uma função e indica sua direção. Se a derivada em um determinado ponto for positiva, a função aumenta, caso contrário, a função diminui. E quanto maior o valor do módulo derivado, maior a taxa de alteração dos valores da função, e maior o ângulo do gráfico da função.

Por exemplo, nas condições de um sistema de coordenadas cartesianas, o valor da derivada no ponto M (0,0) igual a +25 significa que, em um determinado ponto, quando o valor é deslocado $$$x$ direito a unidade arbitrária, valor $$$y$ aumenta em 25 unidades convencionais. No gráfico, parece um ângulo de elevação bastante íngreme $$$y$ de um dado ponto.

Outro exemplo Um valor derivativo de -0,1 significa que, quando compensado $$$x$ por unidade convencional, valor $$$y$ diminui em apenas 0,1 unidade convencional. Ao mesmo tempo, no gráfico de funções, podemos observar uma inclinação quase imperceptível. Fazendo uma analogia com a montanha, parece que descemos muito lentamente a suave encosta da montanha, ao contrário do exemplo anterior, onde tivemos que tomar picos muito íngremes :)

Assim, depois de diferenciar a função $$$ERR (x) = \ soma \ limites_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ por coeficientes $$$a$ e $$$b$ , definimos as equações de derivadas parciais de primeira ordem. Após definir as equações, obtemos um sistema de duas equações, decidindo quais podemos escolher esses valores dos coeficientes $$$a$ e $$$b$ em que os valores das derivadas correspondentes em determinados pontos mudam por um valor muito, muito pequeno, e, no caso da solução analítica, eles não mudam. Em outras palavras, a função de erro nos coeficientes encontrados atinge um mínimo, uma vez que os valores das derivadas parciais nesses pontos serão zero.

Assim, de acordo com as regras de diferenciação, a equação da derivada parcial de 1ª ordem em relação ao coeficiente $$$a$ assumirá a forma:

$$

$$2na + 2b \ sum \ limits_ {i = 1} ^ nx_i - 2 \ sum \ limits_ {i = 1} ^ ny_i = 2 (na + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i)$$

Equação da derivada parcial de 1ª ordem em relação a $$$b$ assumirá a forma:

$$

$$2a \ sum \ limits_ {i = 1} ^ nx_i + 2b \ sum \ limits_ {i = 1} ^ nx ^ 2_i - 2 \ sum \ limits_ {i = 1} ^ nx_iy_i = 2 \ sum \ limits_ {i = 1} ^ nx_i (a + b \ soma \ limites_ {i = 1} ^ nx_i - \ soma \ limites_ {i = 1} ^ ny_i)$$

Como resultado, obtivemos um sistema de equações que possui uma solução analítica bastante simples:

\ begin {equação *}
\ begin {cases}
na + b \ soma \ limites_ {i = 1} ^ nx_i - \ soma \ limites_ {i = 1} ^ ny_i = 0
\\
\ soma \ limites_ {i = 1} ^ nx_i (a + b \ soma \ limites_ {i = 1} ^ nx_i - \ soma \ limites_ {i = 1} ^ ny_i) = 0
\ end {cases}
\ end {equação *}

Antes de resolver a equação, pré-carregue, verifique o carregamento correto e formate os dados.

Baixar e formatar dados

Deve-se notar que, devido ao fato de que, para a solução analítica e, posteriormente, para a descida do gradiente e do gradiente estocástico, usaremos o código em duas variações: usando a biblioteca NumPy e sem usá-lo, precisaremos formatar os dados adequadamente (consulte código).

Visualização

Agora, após o download dos dados, em primeiro lugar, verificamos o carregamento correto e, finalmente, formatamos os dados, realizaremos a primeira visualização. Freqüentemente, o método pairplot da biblioteca Seaborn é usado para isso. Em nosso exemplo, devido aos números limitados, não faz sentido usar a biblioteca Seaborn . Usaremos a biblioteca normal do Matplotlib e examinaremos apenas o gráfico de dispersão.


Cronograma nº 1 “Dependência de receita em relação ao mês do ano”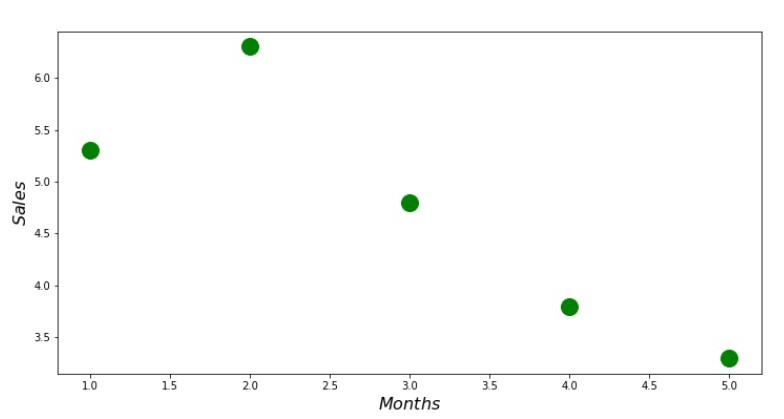

Solução analítica

Usaremos as ferramentas mais comuns em python e resolveremos o sistema de equações:

\ begin {equação *}
\ begin {cases}
na + b \ soma \ limites_ {i = 1} ^ nx_i - \ soma \ limites_ {i = 1} ^ ny_i = 0
\\
\ soma \ limites_ {i = 1} ^ nx_i (a + b \ soma \ limites_ {i = 1} ^ nx_i - \ soma \ limites_ {i = 1} ^ ny_i) = 0
\ end {cases}
\ end {equação *}

De acordo com a regra de Cramer, encontramos um determinante comum, bem como determinantes por $$$a$ e por $$$b$ , após o que, dividindo o determinante por $$$a$ no determinante comum - encontramos o coeficiente $$$a$ , da mesma forma, encontre o coeficiente $$$b$ .


Aqui está o que temos:



Assim, os valores do coeficiente são encontrados, a soma dos desvios ao quadrado é definida. Traçamos uma linha reta no histograma de dispersão de acordo com os coeficientes encontrados.


Anexo No. 2 “Respostas Corretas e Estimadas”



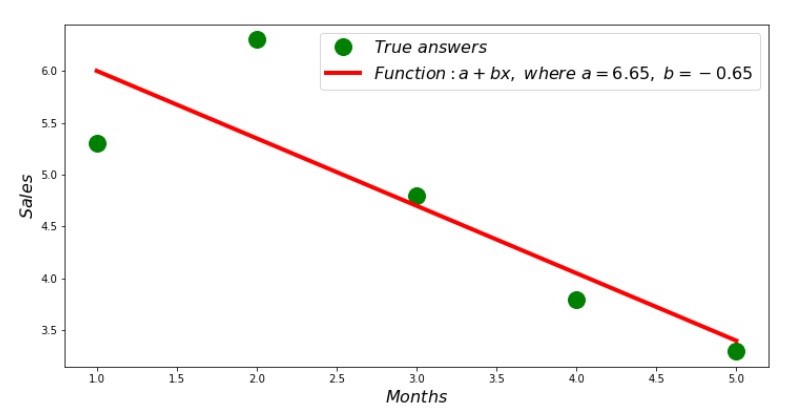
Você pode ver a programação de desvio de cada mês. No nosso caso, não podemos extrair nenhum valor prático significativo, mas satisfazeremos a curiosidade de quão bem a equação de regressão linear simples caracteriza a dependência da receita no mês do ano.


Anexo No. 3 “Desvios,%”



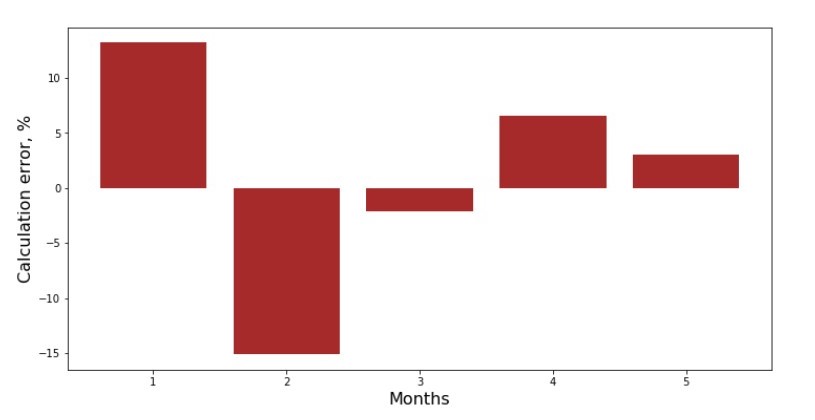
Não é perfeito, mas concluímos nossa tarefa.

Escrevemos uma função que, para determinar os coeficientes $$$a$ e $$$b$ usa a biblioteca NumPy , mais precisamente - escreveremos duas funções: uma usando uma matriz pseudo-inversa (não recomendada na prática, pois o processo é computacionalmente complexo e instável) e a outra usando uma equação de matriz.


Compare o tempo necessário para determinar os coeficientes $$$a$ e $$$b$ , de acordo com os 3 métodos apresentados.




Em uma pequena quantidade de dados, é apresentada uma função "auto-escrita" que encontra os coeficientes usando o método Cramer.

Agora você pode seguir para outras maneiras de encontrar os coeficientes $$$a$ e $$$b$ .

Descida de gradiente

Primeiro, vamos definir o que é um gradiente. De uma maneira simples, um gradiente é um segmento que indica a direção do crescimento máximo de uma função. Por analogia com uma subida, onde o gradiente parece, há a subida mais íngreme até o topo da montanha. Desenvolvendo o exemplo da montanha, lembramos que de fato precisamos da descida mais íngreme para alcançar a planície o mais rápido possível, ou seja, o mínimo - o local em que a função não aumenta ou diminui. Neste ponto, a derivada será zero. Portanto, não precisamos de um gradiente, mas de um anti-gradiente. Para encontrar o anti-gradiente, basta multiplicar o gradiente por -1 (menos um).

Chamamos a atenção para o fato de que uma função pode ter vários mínimos e, tendo descido para um deles de acordo com o algoritmo proposto abaixo, não conseguiremos encontrar outro mínimo possivelmente mais baixo que o encontrado. Relaxe, não estamos em perigo! No nosso caso, estamos lidando com um único mínimo, já que nossa função $$$\ soma \ limites_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ no gráfico há uma parábola comum. E como todos devemos saber muito bem do curso escolar de matemática, a parábola tem apenas um mínimo.

Depois de descobrirmos por que precisamos de um gradiente, e também que o gradiente é um segmento, ou seja, um vetor com coordenadas dadas, que são exatamente os mesmos coeficientes $$$a$ e $$$b$ podemos implementar descida gradiente.

Antes de começar, sugiro ler apenas algumas frases sobre o algoritmo de descida:

• Determinamos as coordenadas dos coeficientes de maneira pseudo-aleatória $$$a$ e $$$b$ . Em nosso exemplo, determinaremos os coeficientes próximos de zero. Essa é uma prática comum, mas cada prática pode ter sua própria prática.
• Da coordenada $$$a$ subtrair o valor da derivada parcial da 1ª ordem no ponto $$$a$ . Portanto, se a derivada for positiva, a função aumentará. Portanto, tirando o valor da derivada, nos moveremos na direção oposta do crescimento, ou seja, na direção da descida. Se a derivada é negativa, então a função nesse ponto diminui e, tirando o valor da derivada, avançamos em direção à descida.
• Realizamos uma operação semelhante com a coordenada $$$b$ : subtraia o valor da derivada parcial no ponto $$$b$ .
• Para não pular o mínimo e não voar para o espaço distante, é necessário definir o tamanho da etapa em direção à descida. Em geral, você pode escrever um artigo inteiro sobre como definir corretamente a etapa e como alterá-la durante a descida para reduzir o custo dos cálculos. Mas agora temos uma tarefa um pouco diferente e estabeleceremos o tamanho do passo pelo método científico de "cutucar" ou, como dizem nas pessoas comuns, empiricamente.
• Depois que somos das coordenadas dadas $$$a$ e $$$b$ subtraídos os valores dos derivativos, obtemos novas coordenadas $$$a$ e $$$b$ . Demos o próximo passo (subtração), já a partir das coordenadas calculadas. E assim o ciclo começa repetidamente, até que a convergência necessária seja alcançada.

Isso é tudo! Agora estamos prontos para ir em busca do desfiladeiro mais profundo da Fossa das Marianas. Descer.




Mergulhamos no fundo da Fossa das Marianas e lá encontramos os mesmos valores dos coeficientes $$$a$ e $$$b$ , o que era de fato esperado.

Vamos fazer outro mergulho, só que desta vez, o preenchimento de nosso veículo de alto mar será outras tecnologias, a saber, a biblioteca NumPy .



Valores do coeficiente $$$a$ e $$$b$ imutável.

Vejamos como o erro mudou durante a descida do gradiente, ou seja, como a soma dos desvios ao quadrado mudou a cada etapa.


Gráfico №4 “A soma dos quadrados dos desvios na descida do gradiente”



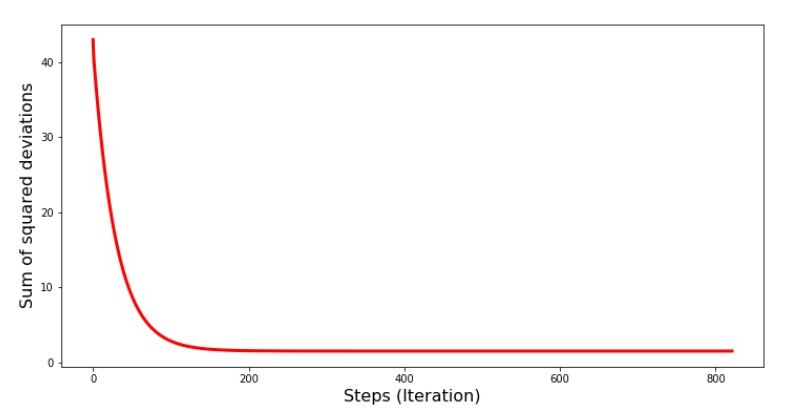
No gráfico, vemos que a cada passo o erro diminui e, após um certo número de iterações, observamos uma linha praticamente horizontal.

Por fim, estimamos a diferença no tempo de execução do código:




Talvez estejamos fazendo algo errado, mas, novamente, uma função simples "auto-escrita" que não usa a biblioteca NumPy está adiantada, usando a função usando a biblioteca NumPy .

Mas não paramos, mas avançamos para o estudo de outra maneira interessante de resolver a equação da regressão linear simples. Me encontre!

Descida do gradiente estocástico

Para entender rapidamente o princípio de operação da descida estocástica do gradiente, é melhor determinar suas diferenças da descida normal do gradiente. Nós, no caso de descida de gradiente, nas equações de derivadas de $$$a$ e $$$a$ usou as somas dos valores de todos os atributos e as respostas verdadeiras disponíveis na amostra (ou seja, as somas de todos $$$x_i$ e $$$y_i$ ) Na descida do gradiente estocástico, não usaremos todos os valores disponíveis na amostra; em vez disso, de maneira pseudo-aleatória, escolheremos o chamado índice de amostra e usaremos seus valores.

Por exemplo, se o índice é determinado pelo número 3 (três), pegamos os valores $$$x_3 = 3$ e $$$y_3 = $ 4,$ , substituímos os valores nas equações das derivadas e determinamos as novas coordenadas. Depois de determinar as coordenadas, novamente determinamos pseudo-aleatoriamente o índice da amostra, substituímos os valores correspondentes ao índice nas equações diferenciais parciais e determinamos as coordenadas $$$a$ e $$$a$ etc. antes da convergência esverdeada . À primeira vista, pode parecer que isso pode funcionar, mas funciona. É verdade que vale a pena notar que nem todas as etapas reduzem o erro, mas a tendência certamente existe.

Quais são as vantagens da descida do gradiente estocástico em relação ao habitual? Se o tamanho da nossa amostra é muito grande e medido em dezenas de milhares de valores, é muito mais fácil processar, digamos, milhares deles aleatoriamente do que a amostra inteira. Nesse caso, a descida do gradiente estocástico é iniciada. No nosso caso, é claro, não perceberemos uma grande diferença.

Nós olhamos para o código.




Examinamos cuidadosamente os coeficientes e nos deparamos com a pergunta "Como assim?". Temos outros valores dos coeficientes $$$a$ e $$$b$ . Talvez a descida do gradiente estocástico tenha encontrado parâmetros mais ótimos da equação? Infelizmente, não. Basta observar a soma dos desvios quadrados e ver que, com os novos valores dos coeficientes, o erro é maior. Não se apresse ao desespero. Traçamos a alteração de erro.


Gráfico №5 “A soma dos quadrados dos desvios na descida do gradiente estocástico”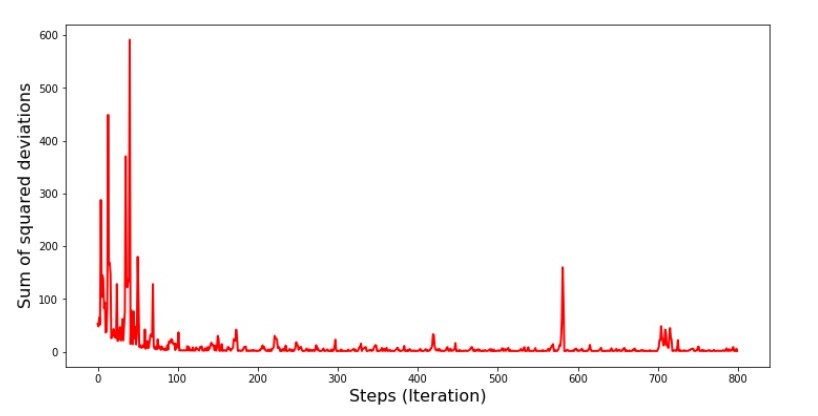



Tendo analisado a programação, tudo se encaixa e agora vamos consertar tudo.

Então o que aconteceu? O seguinte aconteceu.Quando selecionamos aleatoriamente um mês, é para o mês selecionado que nosso algoritmo procura reduzir o erro no cálculo da receita. Depois, selecionamos outro mês e repetimos o cálculo, mas já reduzimos o erro para o segundo mês selecionado. E agora, lembremos que, nos primeiros dois meses, nos desviamos significativamente da linha da equação da regressão linear simples. Isso significa que, quando qualquer um desses dois meses é selecionado e, reduzindo o erro de cada um deles, nosso algoritmo aumenta seriamente o erro em toda a amostra. Então o que fazer? A resposta é simples: você precisa reduzir a etapa de descida. Afinal, diminuindo a etapa de descida, o erro também deixará de “pular” para cima e para baixo. Em vez disso, o erro "ignorar" não será interrompido, mas não será tão rápido :) Vamos verificar.




Gráfico №6 “A soma dos desvios ao quadrado na descida do gradiente estocástico (80 mil passos)”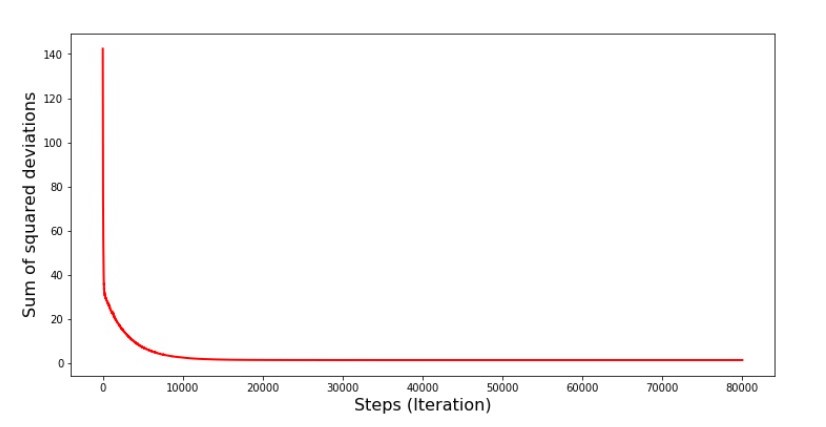



Os valores dos coeficientes melhoraram, mas ainda não são ideais. Hipoteticamente, isso pode ser corrigido dessa maneira. Por exemplo, nas últimas 1000 iterações, escolhemos os valores dos coeficientes com os quais o erro mínimo foi cometido. É verdade que, para isso, teremos que anotar os próprios valores do coeficiente. Não faremos isso, mas sim prestar atenção ao cronograma. Parece bom, e o erro parece diminuir uniformemente. Este não é realmente o caso. Vamos dar uma olhada nas primeiras 1000 iterações e compará-las com a última.


Tabela No. 7 “A soma dos quadrados dos desvios do SGD (primeiros 1000 passos)”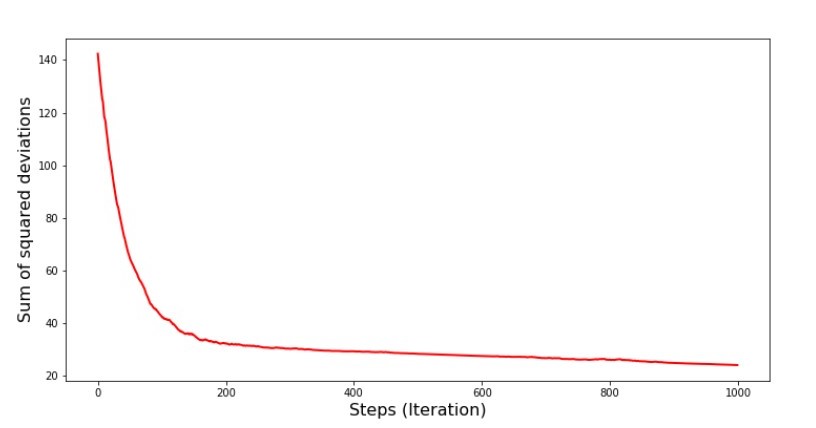



Gráfico No. 8 “A soma dos quadrados dos desvios do SGD (últimos 1000 passos)”



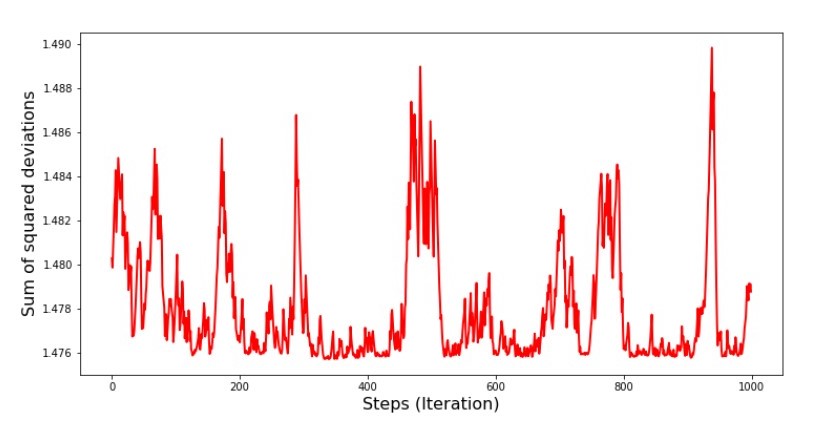No início da descida, observamos uma diminuição bastante uniforme e acentuada do erro. Nas últimas iterações, vemos que o erro gira em torno de um valor de 1.475 e, em alguns pontos, é igual a esse valor ideal, mas depois sobe de qualquer maneira ... Mais uma vez, posso anotar os valores dos coeficientes$$$a$ e $$b e selecione aqueles para os quais o erro é mínimo. No entanto, tivemos um problema mais sério: tivemos que dar 80 mil etapas (consulte o código) para obter valores próximos do ideal. E isso já contradiz a idéia de economizar tempo computacional com descida estocástica do gradiente em relação ao gradiente. O que pode ser corrigido e aprimorado? Não é difícil perceber que, nas primeiras iterações, diminuímos com confiança e, portanto, devemos deixar um grande passo nas primeiras iterações e reduzi-lo à medida que avançamos. Não faremos isso neste artigo - ele já se arrastou. Quem quiser pode pensar em como fazer isso, não é difícil :)Agora, realizaremos uma descida estocástica de gradiente usando a bibliotecaNumPy$b$

(e não tropeçaremos nas pedras que identificamos anteriormente)




Os valores foram quase os mesmos que durante a descida sem usar o NumPy . No entanto, isso é lógico.

Descobriremos quanto tempo as descidas estocásticas do gradiente nos levaram.




Quanto mais longe na floresta, mais escuras as nuvens: novamente a fórmula "auto-escrita" mostra o melhor resultado. Tudo isso sugere que deve haver maneiras ainda mais sutis de usar a biblioteca NumPy , o que realmente acelera as operações de cálculos. Neste artigo, não descobriremos sobre eles. Haverá algo em que pensar à sua vontade :)

Resumir

Antes de resumir, gostaria de responder à pergunta que provavelmente surgiu de nosso querido leitor. Por que, de fato, tal "tormento" com descidas, por que temos que subir e descer a montanha (principalmente para baixo) para encontrar a planície preciosa, se temos um dispositivo tão poderoso e simples em nossas mãos, na forma de uma solução analítica que nos teleporta instantaneamente para lugar certo?

A resposta a esta pergunta está na superfície. Agora examinamos um exemplo muito simples no qual a resposta verdadeira$$y eu depende de um atributo$y_i$$$$x_i$ .Na vida, isso não é visto com frequência, então imagine que temos sinais de 2, 30, 50 ou mais. Adicione a isso milhares ou mesmo dezenas de milhares de valores para cada atributo. Nesse caso, a solução analítica pode não passar no teste e falhar. Por sua vez, a descida do gradiente e suas variações nos aproximam lenta mas seguramente do objetivo - o mínimo da função. E não se preocupe com a velocidade - provavelmente também analisaremos métodos que nos permitirão definir e ajustar o comprimento da etapa (ou seja, velocidade).

E agora, na verdade, um breve resumo.

Em primeiro lugar, espero que o material apresentado no artigo ajude os iniciantes a "datar os cientistas" para entender como resolver as equações da regressão linear simples (e não apenas).

Em segundo lugar, examinamos várias maneiras de resolver a equação. Agora, dependendo da situação, podemos escolher o que melhor se adequa à solução do problema.

Em terceiro lugar, vimos o poder de configurações adicionais, a saber, o comprimento do passo da descida do gradiente. Este parâmetro não pode ser negligenciado. Como observado acima, para reduzir o custo dos cálculos, o comprimento do passo deve ser alterado ao longo da descida.

Quarto, no nosso caso, as funções "auto-escritas" mostraram o melhor resultado temporal dos cálculos. Provavelmente, isso não se deve ao uso mais profissional dos recursos da biblioteca NumPy. Mas, seja como for, a conclusão é a seguinte. Por um lado, às vezes vale a pena questionar as opiniões estabelecidas e, por outro, nem sempre vale a pena complicar as coisas - pelo contrário, às vezes uma maneira mais simples de resolver um problema é mais eficaz. E como nosso objetivo era analisar três abordagens na resolução da equação da regressão linear simples, o uso de funções "auto-escritas" foi suficiente para nós.

← Trabalho anterior do autor - “Estudamos a afirmação do teorema do limite central usando a distribuição exponencial”$\leftarrow$
→ O próximo trabalho do autor - “Trazemos a equação da regressão linear para a forma matricial”$\rightarrow$

Literatura (ou algo parecido)

1. Regressão linear

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. Método dos mínimos quadrados

mathprofi.ru/metod_naimenshih_kvadratov.html

3. Derivado

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4. Gradient

math /proizvodnaja_po_napravleniju_i_gradient.html

5. Descida gradiente

habr.com/en/post/471458

habr.com/en/post/307312

artemarakcheev.com//2017-12-31/linear_regression

6. Biblioteca NumPy

docs.scipy.org/doc/ numpy-1.10.1 / reference / generate / numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2. html