Examinamos o método de Monte Carlo , hoje veremos como a mente do computador funciona em 2048 usando o bom e velho minimax com recorte alfa-beta.

O artigo foi escrito com o apoio da EDISON, uma empresa que desenvolve aplicativos móveis e fornece serviços de teste de software .
Solução espionada pelo usuário stackoverflow
 ovolve
ovolve , que observou na discussão
como ensinar à IA o jogo 2048 .
Tradução de comentários de ovolveEu sou o autor do programa mencionado neste tópico. Você pode ver a IA
em ação ou ver
o código .
Atualmente, o programa vence em cerca de 90% dos casos executando scripts java em um navegador no meu laptop, gastando 100 milissegundos para pensar no curso, funcionando, embora não perfeitamente, mas muito bem.
Como o jogo é um espaço de estado discreto com informações completas, na verdade, é um jogo baseado em turnos, como xadrez e damas, usei os mesmos métodos que mostraram seu desempenho nesses jogos, ou seja,
pesquisa minimax com
recorte alfa-beta . Como os links fornecem muitas informações sobre esse algoritmo, falarei sobre as duas heurísticas principais que usei na
função de estimativa estática e formalizei muitas das suposições intuitivas feitas por outras pessoas aqui.

Monotonia
Essa heurística tenta garantir que todos os valores do bloco aumentem ou diminuam a esquerda / direita e para cima / para baixo. Somente essa heurística reflete a conjectura de que muitos outros mencionaram que blocos mais valiosos devem ser agrupados em um canto. Como regra, isso evita o acúmulo de ladrilhos menos valiosos e mantém o tabuleiro organizado, à medida que ladrilhos menores passam por cascatas em outros maiores.
Aqui está uma captura de tela de uma grade completamente monótona. Eu entendi essa situação executando um algoritmo com a função eval instalada, a fim de ignorar outras heurísticas e levar em conta apenas a monotonia.

Suavidade (suavidade, uniformidade)
A heurística acima, por si só, tende a criar estruturas nas quais as células vizinhas são reduzidas em valor; no entanto, é claro, as vizinhas devem ter o mesmo significado para combinar. Portanto, a heurística da suavidade mede simplesmente a diferença de valores entre os blocos adjacentes, tentando minimizar seu número.
Um comentarista do Hacker News forneceu uma
formalização interessante dessa idéia em termos de teoria dos grafos.
Tradução da formalização com Hacker NewsOntem mostrei este jogo a um colega, um amante da teoria dos grafos, e também decidimos pensar em como resolver esse jogo usando IA.
A solução mais simples é o minimax, que, a meu ver, é implementado muito bem. Se alguém aqui não estiver familiarizado com o minimax, o OP escreveu um código muito elegante e bem comentado, que seria um ótimo tutorial.
A abordagem menos intensiva em termos de computação que propusemos foi modelar o estado do jogo na forma de um gráfico G (V, E) , em que V é um conjunto de blocos ativos e E é um conjunto de arestas que conectam blocos adjacentes ponderados pela função c (v1, v2) , que retorna o valor absoluto da diferença entre os dois blocos. Para cada solução, a IA escolhe uma jogada que minimiza a soma dos pesos de todas as arestas no novo estado do jogo.
A razão para isso é que a única maneira de progredir no jogo é ter peças com os mesmos valores próximos umas das outras, para as quais o peso em G será 0. Portanto, a IA deve tentar minimizar o peso total. No final, haverá um grande número nas placas com um grande peso de arestas nos ladrilhos adjacentes; portanto, a IA tentará manter esses ladrilhos ao lado de outros ladrilhos grandes para minimizar a diferença.
Como o jogo é estocástico, a abordagem que eu descrevi pode não funcionar no pior dos casos, mas também pode ser aplicada à solução minimax existente como uma função de peso para cada nó na árvore.
Aqui está uma captura de tela de uma malha perfeitamente lisa, gentilmente fornecida por este excelente
garfo falso .
(link para o arquivo da web, enquanto os scripts Java na página funcionam e você pode usar o teclado para mover-se em qualquer direção - nota do tradutor).Ladrilhos soltos
E, finalmente, há uma penalidade por ter poucas peças gratuitas, pois as opções podem terminar rapidamente quando o campo de jogo fica muito apertado.
E isso é tudo! A pesquisa no espaço do jogo e a otimização desses critérios oferecem um desempenho surpreendentemente bom. Um dos benefícios de usar uma abordagem genérica como essa, em vez de uma estratégia de movimentação explicitamente codificada, é que o algoritmo pode frequentemente encontrar soluções interessantes e inesperadas. Se você observar seu progresso, ele geralmente faz movimentos surpreendentes, mas eficazes, como a mudança repentina de paredes ou cantos, perto dos quais ele constrói seu jogo.

Pequena mudança
A captura de tela demonstra o poder dessa abordagem. Eu removi o limite do bloco (para que eles continuem a crescer depois de chegar a 2048), e aqui está o melhor resultado após oito testes.
Sim, isso é 4096 junto com 2048. =) Isso significa que ele alcançou o esquivo 2048 em uma placa.
O código Java-Script para minimax com recorte alfa-beta e função de avaliação estática do ovove do usuário do stackoverflow é fornecido abaixo no artigo.
O método minimax é dedicado a vários excelentes artigos de habr, portanto omitimos a explicação acadêmica detalhada do que ele consiste. Para aqueles que se
juntaram à comunidade de TI, ouvi
recentemente os belos termos "minimax" e "recorte alfa-beta", mas não sabem o que isso significa, vamos tentar, literalmente, em alguns parágrafos, explicar o significado mais geral.
Minimax
Em alguns jogos, o processo de um jogo entre dois jogadores (que fazem um lance por sua vez) pode ser representado como uma chamada árvore de opções. Em cada posição específica, cada jogador geralmente tem uma escolha entre diferentes opções para sua jogada. E em resposta a cada uma dessas opções, um oponente também pode ser como de várias maneiras.
Fragmento de uma árvore de opçõesComo em qualquer momento do jogo há informações completas sobre o estado do campo de jogo, o estado atual da posição sempre pode ser estimado com precisão. Essa função é chamada
função de avaliação estática ou
SFO abreviado. Além disso, quanto mais importante é essa função ao avaliar uma posição específica, mais vantajosa é a posição de um jogador (vamos chamá-lo de
jogador maximizador ). Quanto menor o valor numérico dessa função ao avaliar uma posição, mais vantajosa é a posição para o segundo jogador (vamos chamá-lo de
jogador minimizador ).
Após cada movimento, a posição muda e, portanto, sua pontuação muda. Ao considerar a árvore de opções, cada jogador precisa não apenas preferir aqueles ramos nos quais a classificação é mais favorável para ele. Você também deve evitar aqueles ramos em que a avaliação da posição é favorável ao oponente.
Supõe-se que o oponente também seja guiado pelo racionalismo e também evite opções que possam levá-lo a perder. Ou seja, cada jogador, ao escolher uma opção, prossegue maximizando seu próprio benefício e, ao mesmo tempo, minimizando o lucro do oponente.
Isso é minimax.
Recorte alfa beta
É bastante óbvio: quem calcula uma árvore de uma determinada posição para uma profundidade maior, ele tem mais chances de ganhar. Mas há um incômodo - a árvore de opções nos jogos tem o hábito desagradável de ramificar e crescer exponencialmente a cada nível de aninhamento. As habilidades de contagem de programas e, ainda mais, as pessoas são limitadas, contando "até o fim" está longe de ser sempre possível. Pode facilmente acontecer que o jogador tenha contado até uma posição em que tenha uma boa avaliação do campo de jogo, mas literalmente no próximo nível (ilegível), o oponente tem a oportunidade de fazer um movimento que muda radicalmente a estimativa de posição para o oposto.
Quem é o culpado e o que fazer? A complexidade computacional é responsável pelo percurso completo da árvore; propõe-se combater cortando galhos desnecessários. Se o jogador que está avaliando a posição vê que algum ramo da árvore de opções:
ou menos rentável para ele do que outros ramos que já foram analisados,
ou mais benéfico para o oponente do que outros ramos que já foram analisados,
então o jogador descarta esse ramo, não perde tempo e recursos ao considerar subopções deste ramo obviamente pior para ele.
Isso permite que você aloque mais recursos de computação para calcular ramificações mais favoráveis a uma maior profundidade de renderização na árvore de opções. No processo de avaliação do campo de jogo em diferentes níveis da árvore de opções, o jogador opera com dois coeficientes dinamicamente variáveis -
alfa (o valor do SFD que é minimamente encontrado no ramo - ou seja, mais favorável para o jogador que minimiza) e
beta (o valor do SFD que é mais encontrado no ramo - ou seja. mais favorável para o jogador maximizador). Em cada nível, comparar o SFD da posição atual com
os coeficientes
alfa e
beta permite varrer (sem calculá-los completamente) ramos que são
menos favoráveis para o jogador que avalia a posição e / ou
mais benéficos para o oponente.
Este é um recorte alfa beta.
Função minimax recursiva com recorte alfa beta
2048 com AI é implementado como um aplicativo Excel com macros VBA, é assim que o algoritmo minimax com recorte alfa beta parece um desprezível visual basic. Fornecer código no java-script function AI(grid) { this.grid = grid; }
Função de Avaliação Estática
Como em cada nível da árvore de opções é necessário avaliar o campo de jogo (para decidir para qual dos jogadores, a posição estimada é realmente mais vantajosa), você precisa decidir quais critérios distinguem uma boa posição da ruim.
Assumimos que o jogador que maximiza é a pessoa (ou AI) que decide em qual das 4 direções (para cima, esquerda, direita, baixo) deve mover todas as peças. Um jogador que minimiza é a sub-rotina insidiosa que gera aleatoriamente 2 ou 4 nos locais mais inadequados.
O SFO é compilado do ponto de vista de um jogador maximizador. Quanto maior a classificação SFD para o campo de jogo, melhor a posição para o "maximalist". Quanto menor - mais agradável é a posição no quadro para o "minimalista".
No caso de 2048 - que fatores são considerados favoráveis para quem move as peças?
Monotonia
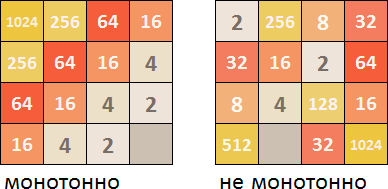
Em primeiro lugar, é desejável que as peças sejam dispostas em ordem crescente / decrescente em algumas direções. Se isso não for feito, quando novas peças forem geradas, o campo de jogo rapidamente ficará entupido com peças dispostas aleatoriamente de tamanhos diferentes, que não podem ser imediatamente conectados normalmente entre si.
No Distrito Federal da Sibéria, você precisa olhar em todas as quatro direções (de cima para baixo, da esquerda para a direita, da direita para a esquerda, de baixo para cima) e calcular onde os blocos são uma progressão crescente ou decrescente. Se em progressão houver blocos que não se encaixam na série geral, isso reduz o coeficiente numérico da monotonia. A partir dos 4 coeficientes para todas as direções, é selecionado o melhor, que é levado em consideração no valor total do Distrito Federal da Sibéria.
Suavidade

Além disso, seria mais preferível se a progressão de ficar em uma fileira de peças não estivesse apenas aumentando, mas não diminuindo (ou, em vez de diminuir a linha, é preferível a não aumentar), ou seja, é bom quando as mesmas peças estiverem próximas, o que lhes permite colapsar em uma, ganhando pontos e aumentando o espaço livre no campo de jogo.
Portanto, o Distrito Federal da Sibéria está procurando as mesmas peças adjacentes no campo de jogo e leva em consideração o número desses pares em um coeficiente especial.
Células vazias

Obviamente, quanto mais espaço livre, mais espaço para manobra e menos chances de perder rapidamente.
A SFO considera as células vazias no campo e, quanto mais, a posição é considerada mais lucrativa para o jogador maximizador.
Ladrilho máximo
Como o principal neste jogo é colocar um bloco grande em campo, quanto melhor - 2048, 4096, 8192 (ou o que você tiver força e paciência), as opções em que o valor máximo do bloco é mais devem ser consideradas como o SFD mais lucrativo.
Distrito Federal da Sibéria para 2048
Implementação do Distrito Federal Siberiano como uma macro VBA Fornecer código no java-script function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
O próprio aplicativo Excel
pode ser baixado do Google .
A funcionalidade do aplicativo é descrita
em um artigo anterior, onde o AI é reproduzido usando o método Monte Carlo . A solução de hoje foi adicionada ao Monte Carlo existente.
Todos os artigos das séries AI e 2048
- Monte Carlo
- Recorte beta Minimax + alfa
- Aguardando o máximo
- Rede neural