Algoritmo de Pesquisa Difusa do TextRadar - Abordagens básicas

Algoritmo de Pesquisa Difusa do TextRadar - Abordagens básicas

Diferentemente das comparações de cadeias difusas, quando as duas cadeias comparadas são equivalentes, a cadeia de pesquisa e a cadeia de dados são destacadas na tarefa de pesquisa difusa, e é necessário determinar não o grau de similaridade das duas cadeias, mas o grau de presença da cadeia de pesquisa na cadeia de dados.

Declaração do problema

Uma cadeia de dados e uma cadeia de pesquisa são fornecidas como conjuntos de caracteres arbitrários que consistem em palavras - grupos de caracteres separados por espaços.

É necessário encontrar na linha de dados o conjunto de fragmentos mais próximo da linha de pesquisa pela composição e posição relativa dos caracteres.

Para avaliar a qualidade do resultado da pesquisa, calcule o coeficiente de relevância, cujo valor deve estar no intervalo de 0 a 1, em que 0 deve corresponder à ausência completa de caracteres da linha de pesquisa na linha de dados e 1 deve corresponder à presença da linha de pesquisa na linha de dados na forma sem distorção.

A busca deve ser realizada pela análise caractere por caractere das linhas de origem, levando em consideração o arranjo mútuo de caracteres e palavras nas linhas, mas sem levar em consideração a sintaxe e a morfologia da linguagem.

Descrição do algoritmo

A pesquisa é realizada em várias etapas.

Construção de uma matriz de coincidências

A matriz de correspondência (M) é uma matriz bidimensional, cujo número de colunas corresponde ao comprimento da cadeia de dados e o número de linhas ao comprimento da cadeia de pesquisa. Os elementos da matriz de coincidência assumem os valores 0 ou 1, dependendo se os caracteres correspondentes das linhas coincidem ou não, com exceção dos espaços (separadores de palavras).
A matriz de correspondência para a cadeia de dados "ABCD EF" e a cadeia de pesquisa "ABC" tem o formato:



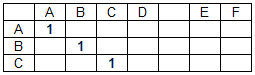
Elemento da matriz de correspondência m (i, j) = 1 se d (i) = s (j), em que D é uma matriz de caracteres da sequência de dados, S é uma matriz de caracteres da sequência de pesquisa, i é um número da coluna da matriz de correspondência M (número de caracteres da sequência de dados ), j é o número da linha da matriz de correspondências (o número do caractere na cadeia de pesquisa). Em outros casos, m (i, j) = 0. Correspondências de separadores de palavras (no nosso caso, espaços) não são levadas em consideração, ou seja: m (i, j) = 0 se d (i) = s (j) = '' .

Diagonais da matriz de correspondência

Elementos da matriz de coincidência M formam diagonais. Os elementos da matriz estão na mesma diagonal se seus índices iej diferirem simultaneamente por +1 ou por - 1.



As diagonais correspondem às posições da sequência de pesquisa na sequência de deslocamentos ao longo da sequência de dados.



Os elementos de uma das diagonais e a mudança correspondente na figura acima são destacados em azul.

A idéia de usar uma sequência de mudanças de linha entre si em um problema de busca difusa remonta à técnica conhecida para detectar sinais de radar contra um fundo de interferência, que envolve o cálculo da função de correlação mútua de sinais de rádio. A função de correlação cruzada determina o grau de similaridade das cópias de dois sinais diferentes v (t) e u (t), deslocados pelo tempo τ em relação um ao outro e é definido como a integral: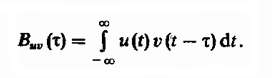



O número total de diagonais é calculado pela fórmula:



Os comprimentos das diagonais são iguais ao comprimento da string de pesquisa.

Grupos de jogos

As unidades que seguem sucessivamente nas diagonais da matriz de coincidência formam grupos de correspondências. Abaixo estão os grupos correspondentes para a sequência de dados “ABCD DEF JH” e a sequência de pesquisa “ABC DE J” - 4 grupos localizados em diagonais diferentes.

Matrizes de projeção

As diagonais da matriz de correspondências e os grupos de correspondências contidos nelas são mapeados para as seções correspondentes da cadeia de pesquisa e linha de dados, formando duas matrizes de projeção - a barra de pesquisa e a linha de dados, respectivamente. Para o nosso exemplo, as matrizes de projeção terão a seguinte aparência:



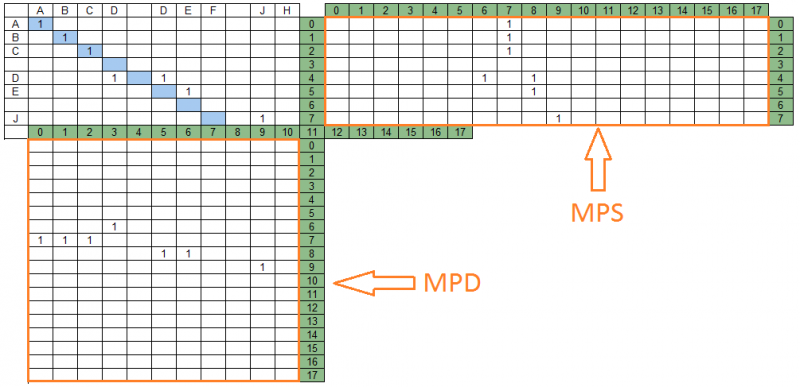
Na figura acima, à direita da matriz de correspondências está a matriz de projeções na cadeia de pesquisa - MPS, abaixo - a matriz de projeções na cadeia de dados MPD. O número de colunas MPS é igual ao número de linhas MPD e igual ao número de diagonais da matriz de correspondências - no nosso exemplo, existem 18.

Pesquise um conjunto de resultados de grupos

Para resolver o problema, é necessário encontrar um conjunto de grupos que “cubra” mais a sequência de pesquisa, com o mínimo de fragmentação (o maior número possível de partes), sem interseções mútuas nas matrizes de projeção e cujo mapeamento para a sequência de dados será o mais próximo da sequência de pesquisa “original” .

Interseção de grupos na matriz de projeção

No nosso exemplo, existem grupos que se cruzam na matriz MPS - na figura abaixo, eles são destacados em vermelho. Além disso, na matriz MPD, esses mesmos grupos não se cruzam, na figura são destacados em verde.



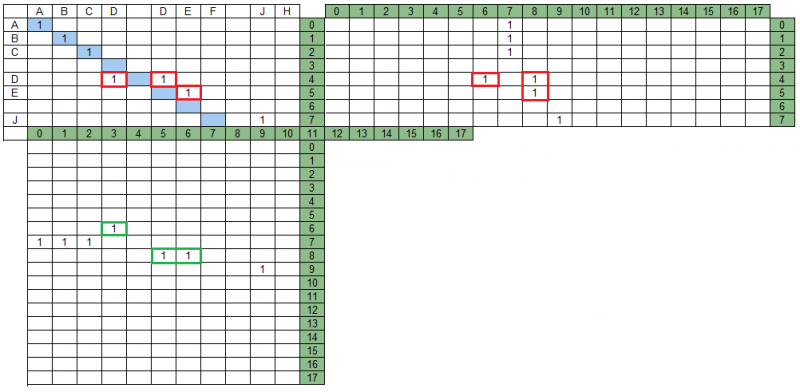
A busca pelo conjunto de grupos resultante implica que nem todos os grupos serão incluídos nele e que alguns dos grupos restantes poderão ser modificados (truncados) ao analisar interseções mútuas de grupos em projeções.

A pesquisa do conjunto de resultados pode ser realizada percorrendo o ciclo “infinito” (o número de iterações do ciclo não excede o número de grupos) da tabela de todos os grupos , nos quais os grupos da matriz de correspondências são inicialmente colocados, a cada iteração da qual as seguintes ações serão executadas:

1. Escolhendo o melhor de acordo com determinados parâmetros (dependendo do contexto do problema que está sendo resolvido) - no caso mais simples, pode ser a escolha do primeiro grupo do maior tamanho encontrado;
2. Posicionamento do melhor grupo na tabela de grupos de resultados e sua remoção da tabela de todos os grupos (cujas linhas são rastreadas);
3. Removendo (ou truncando) da tabela de grupos que se cruzam com o melhor grupo selecionado nas matrizes de grupos de projeção.

O conjunto ideal de grupos para o nosso exemplo é apresentado na figura abaixo - os grupos definidos são destacados em laranja.



O grupo excluído durante o processamento da interseção (interseção na matriz MPS com o melhor grupo da segunda iteração) é destacado em vermelho.

O resultado da pesquisa na linha de dados terá a seguinte aparência:

Cálculo do coeficiente de relevância

Para quantificar os resultados da pesquisa, os comprimentos dos grupos encontrados são comparados com os comprimentos das palavras da sequência de pesquisa (avaliação da composição do grupo), bem como o comprimento total da sequência de pesquisa com o comprimento dos grupos encontrados na sequência de dados. Supõe-se que o significado da avaliação da composição dos grupos encontrados seja superior ao significado da estimativa de extensão na linha de dados, que é levada em consideração nos coeficientes de ponderação da fórmula para o cálculo do coeficiente de relevância:



Onde o coeficiente de composição do grupo é calculado como a razão entre a soma dos comprimentos quadrados dos grupos encontrados e a soma dos comprimentos quadrados das palavras da string de pesquisa:



O fator de comprimento é a proporção entre o comprimento da cadeia de pesquisa e o comprimento total dos grupos encontrados na cadeia de dados. Se o valor obtido dessa maneira for maior que 1, seu valor inverso será obtido:



Para o nosso exemplo:

Escopo estimado da computação

As operações mais intensivas em recursos são:

• determinação da matriz de correspondência M - o número de elementos da matriz é definido como o produto do comprimento da cadeia de pesquisa pelo comprimento da cadeia de dados: L * L;
• definição de matrizes de projeção nos dados e nas seqüências de busca - o número de elementos da matriz será para MPS: (L + L - 1) * L, para MPD: (L + L - 1) * ;
• a formação da tabela de todos os grupos - o número de grupos não excederá o valor L * L / 2;
• procure o conjunto de grupos resultante - o número de iterações do ciclo não excede o número inicial de grupos, ou seja, L * L / 2.

Assim, a quantidade total de cálculos será um múltiplo do produto do comprimento da cadeia de pesquisa pelo comprimento da cadeia de dados:



A linearidade da quantidade de computação em relação ao tamanho dos dados de origem é um argumento importante a favor da aplicação prática do algoritmo.

Não linearidade

Vale ressaltar que a linearidade se deve a um procedimento simplificado para encontrar o conjunto de grupos resultante. No caso geral, se considerarmos todas as opções possíveis para colocar grupos em uma linha de dados, levando em consideração possíveis opções de processamento de interseção e selecionar o melhor conjunto de grupos do conjunto possível, em vez de escolher um grupo a cada iteração do ciclo, a quantidade de cálculos deixará de ser linear em relação ao tamanho dados de origem. A dependência não linear da quantidade de computação no tamanho dos dados de origem limita muito as possibilidades de aplicação prática.

Encontre o equilíbrio

Para garantir o equilíbrio ideal entre a qualidade da pesquisa e a necessidade de recursos, é importante escolher a metodologia de pesquisa correta para o conjunto de grupos resultante, que, como regra, pode ser feito usando os recursos de contexto do problema que está sendo resolvido.

Um suporte de demonstração foi implementado no site textradar.ru , onde você pode testar a operação do algoritmo.

Comparação com análogos: Comparação do algoritmo de pesquisa difusa TextRadar com análogos: Lucene, Sphinx, Yandex, 1C