Uma das tarefas mais difíceis em sistemas de design auxiliados por computador é filetagem ao modelar objetos de formas complexas. Para a construção de filetes, bem como para toda a geometria em CAD, o núcleo geométrico é responsável.

Do ponto de vista do desenvolvedor do kernel, é impossível cobrir todas as opções de arredondamento devido à sua variedade infinita. Nossos matemáticos estão constantemente adicionando novos casos especiais ao núcleo do C3D e recentemente fizeram um arredondamento de três faces (ou arredondamento completo).

Qual é a sua complexidade e como o algoritmo funciona, diz Anna Ladilova, matemática e programadora do C3D Labs.

O que é arredondamento completo?

Suponha que tenhamos um corpo com três cadeias de faces - central (superior) e lateral (direita e esquerda). É necessário substituir a face central por uma superfície de filete que se encaixe suavemente nas faces laterais adjacentes. Essa nova superfície terá arredondamento total. Em geral, possui um raio variável que é detectado automaticamente.

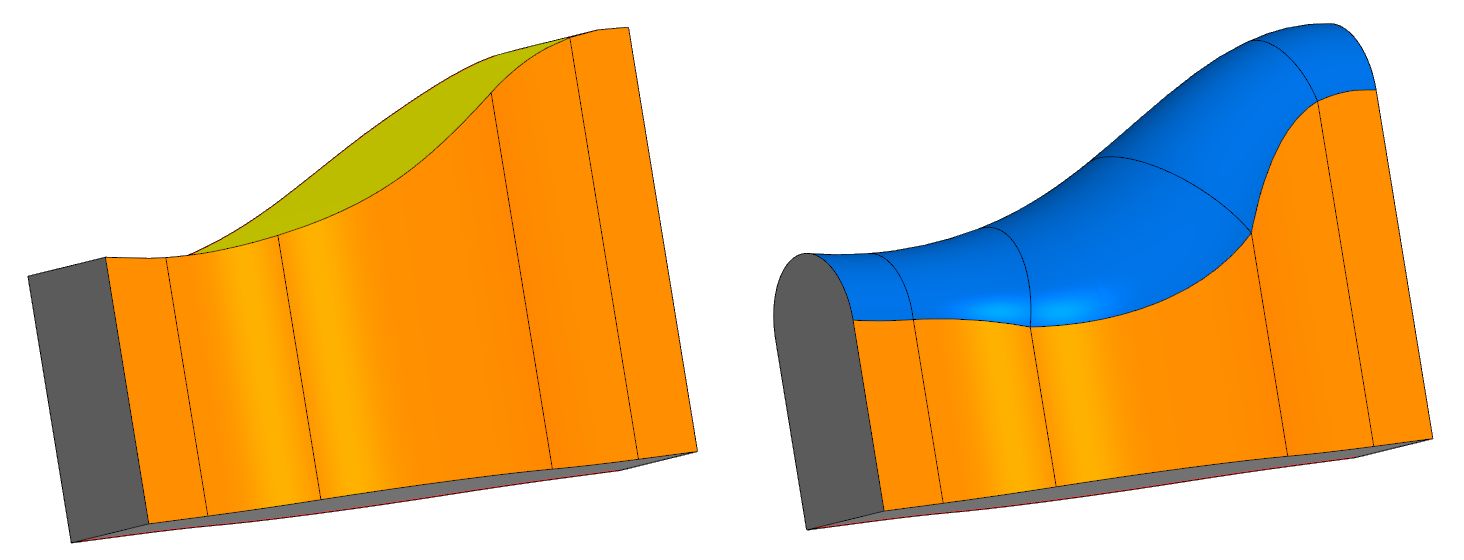
imagem

Em muitos sistemas CAD conhecidos, a operação de filete completa é implementada, mas sua matemática não é divulgada.

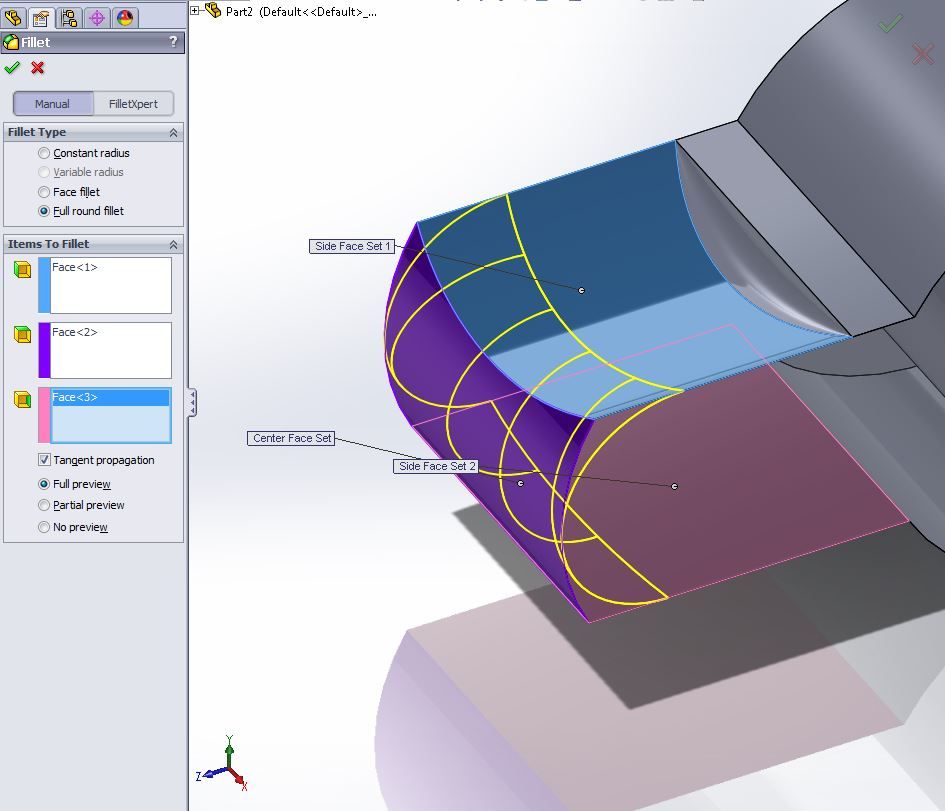imagem

Operação de filete redondo completo do Solidworks

Portanto, desenvolvemos nosso próprio algoritmo. E difere dos algoritmos de outros desenvolvedores.

As operações, embora sejam chamadas de iguais, levam a resultados ligeiramente diferentes. Isso sugere que o SolidWorks fornece uma definição diferente para arredondar três faces.

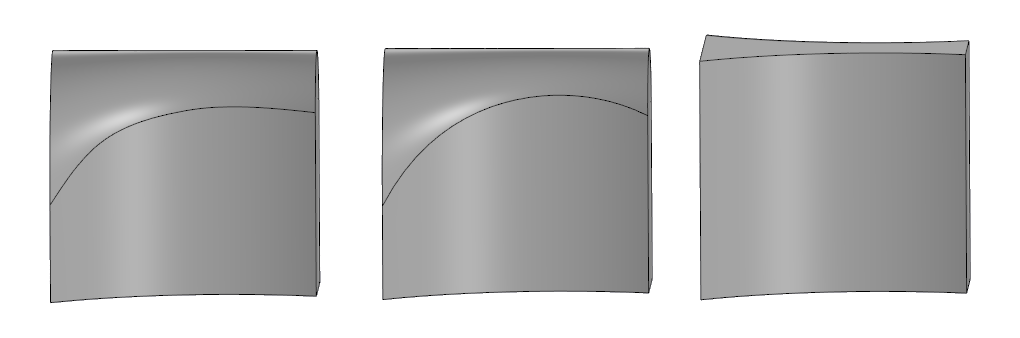imagem

À direita está o modelo original, no centro está o arredondamento completo no SolidWorks, à esquerda - no C3D.

Algoritmo de arredondamento completo

A tarefa de construir qualquer tipo de filetes inclui vários estágios:

Divida a corrente em componentes elementares (para arredondar três faces, são exatamente três faces: esquerda, direita e central).
Organize consistentemente componentes elementares.
Crie uma superfície de filete para cada componente elementar.
Costure as superfícies de filete adjacentes com nervuras.
Para processar as seções finais da cadeia de filetes, ou seja, conectá-las corretamente ao corpo modificado.

O ponto principal neste procedimento é a terceira etapa: construir uma superfície de filete para três faces dadas.

Para construir a superfície desejada, primeiro é necessário determinar as curvas pelas quais o filete toca cada uma das três faces. No caso geral, essas curvas só podem ser construídas como splines que passam por pontos conhecidos que são calculados com antecedência.

Considere como você pode calcular um triplo de pontos - um em cada spline.

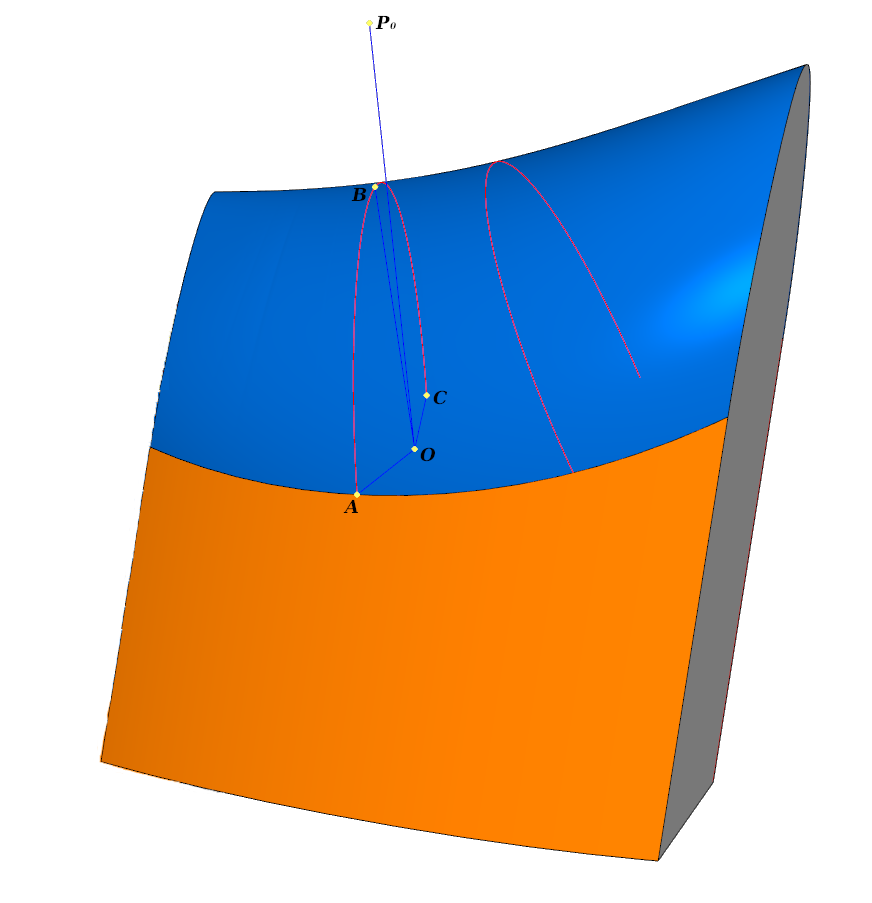
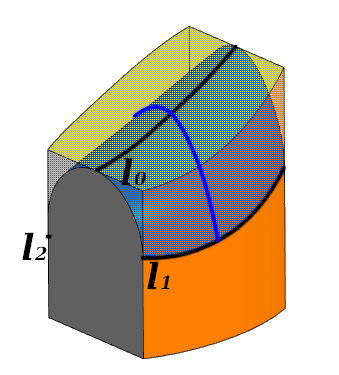imagem

Processamento elementar. O filete toca cada uma das três faces ao longo das curvas ₁₀ ; ₁ ; ₂ . A linha azul mostra a seção transversal

Em cada seção transversal

$ABC$ :

$OA = OB = OC$ - calculado automaticamente
$OA, OB, OC$ ortogonal aos planos tangentes das superfícies nos pontos correspondentes
$p$ ₀ - ponto de ancoragem, fica no plano $ABC$ .

Definimos as superfícies iniciais das faces central, esquerda e direita por vetores de raio em um determinado domínio de definição. Deixe as superfícies laterais serem definidas por vetores de raio

$r$ ₁

$(u, v)$ e

$r$ ₂

$(z, w)$ e o central

$r$ _{0 0}

$(x, y)$ . Introduzimos um parâmetro numérico positivo

$d$ .

Denotar por

$n$ _{0 0}

$(x, y)$ ,

$n$ ₁

$(u, v)$ ,

$n$ ₂

$(z, w)$ normais normais para as superfícies correspondentes, direcionados "para dentro".

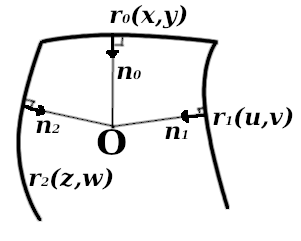imagem

Cruze "seção" ao construir um filete

Exigimos que os fins desses normais se estendam em

$d$ vezes, acertar um ponto - ponto

$O$ .

Em termos de geometria diferencial, nossos requisitos podem ser formulados por um sistema de sete equações com sete parâmetros:

$dn$ _{0 0}

$(x, y)$ =

$dn$ ₁

$(u, v)$ ,

$dn$ _{0 0}

$(x, y)$ =

$dn$ ₂

$(z, w)$ ,
(

$r$ _{0 0}

$(x, y)$ -

$p$ _{0 0}

$r$ ₁

$(u, v)$ -

$p$ _{0 0}

$r$ ₂

$(z, w)$ -

$p$ ₀ ) =

$0$ ,

onde

$d$ - raio variável
$p$ ₀ - ponto de ancoragem
$x, y, u, v, z, w$ - variáveis da área de definição de parâmetros.

Usando algoritmos de métodos numéricos (por exemplo, o método de Newton), encontramos uma solução para este sistema:

$x$ _{0 0}

$y$ _{0 0}

$u$ _{0 0}

$v$ _{0 0}

$z$ _{0 0}

$w$ _{0 0}

$d$ ₀

A solução define pontos de contato com superfícies:

$r$ ₀ ( $x$ _{0 0} $y$ ₀ )
$r$ ₁ ( $u$ _{0 0} $v$ ₀ )
$r$ ₂ ( $z$ _{0 0} $w$ ₀ )

bem como raio

$d$ ₀

Percorrendo um conjunto de pontos

$p$ ₀ , obtemos conjuntos de triplos de pontos tangentes com superfícies a partir das quais você pode restaurar "curvas de toque"

$l$ _{0 0}

$l$ ₁

$l$ ₂ como splites de Hermite passando por pontos calculados.

Escopo [

$t$ _min

$t$ _max ] todas as curvas são iguais e o parâmetro

$t$ _eu corresponde a um ponto

$r$ _0i

$r$ _1i

$r$ _2i . Além disso, essas curvas são usadas para calcular a seção transversal do filete desejada.

Fixamos algum parâmetro

$t$ e calcule os pontos para isso:

$r$ _{0 0} $(x (t), y (t)),$
$r$ ₁ $(u (t), v (t)),$
$r$ ₂ $(z (t), w (t))$ .

Construímos uma curva spline passando por esses pontos e vetores normais ortogonais a eles

$n$ _{0 0}

$(x (t), y (t))$ ,

$n$ ₁

$(u (t), v (t))$ ,

$n$ ₂

$(z (t), w (t))$ em conformidade.

Se a declaração do problema for ligeiramente alterada e a curva for pesquisada em determinados pontos e vetores tangentes nesses pontos, os métodos pelos quais essa spline pode ser implementada podem ser encontrados, por exemplo, no livro de Nikolai Golovanov, “Modelagem Geométrica”.

O livro descreve em detalhes os métodos de arredondamento de uma aresta do corpo, em particular, é mostrado que a seção transversal de um arredondamento pode ser realizada como uma curva NURBS definida por três pontos. Se três faces forem arredondadas, uma curva semelhante será determinada por cinco pontos.

Então, para cada parâmetro

$t$ podemos definir um conjunto de pontos para a construção de NURBS e, portanto, definir cada ponto da seção transversal da superfície do filete. Assim, o problema da construção da superfície é completamente resolvido.

Havia uma pequena pergunta na descrição desta parte do algoritmo - como escolher o conjunto de pontos "corretamente"

$p$ ₀ correspondente à seção transversal através da qual será fácil restaurar as "curvas de toque"

$l$ _{0 0}

$l$ ₁

$l$ ₂ ?

Parece razoável levá-los com alguma curva pré-selecionada. Não entraremos nos detalhes da construção dessa curva, apenas observamos que ela deve ser suave, sem auto-interseções e “mediar” as cadeias de arestas que delimitam a face central à esquerda e à direita.

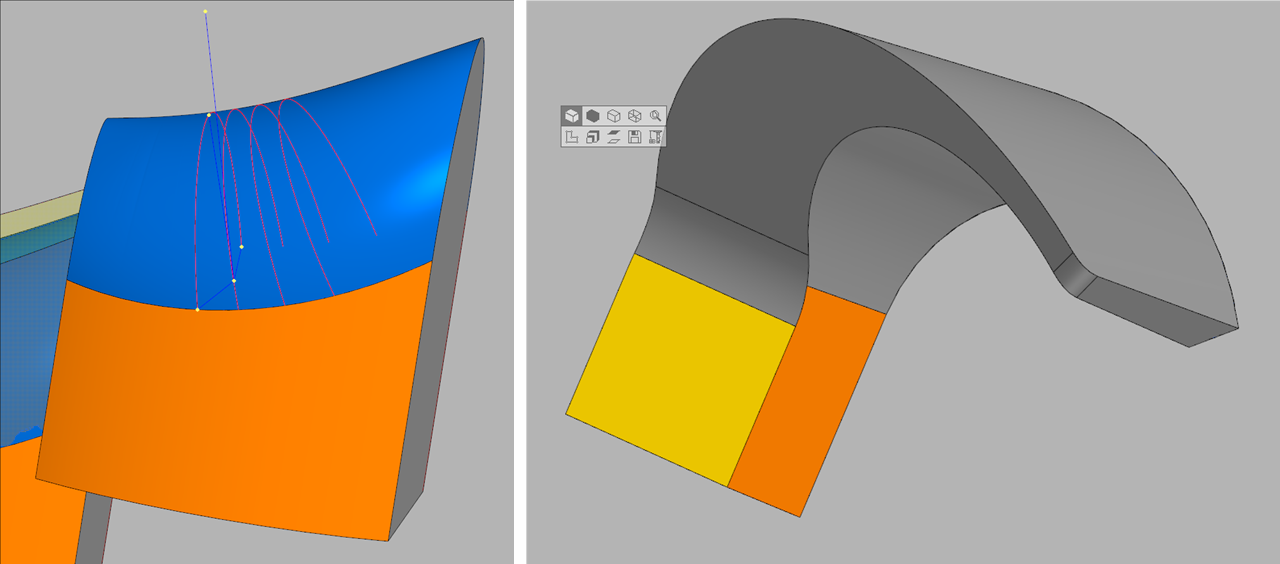imagem

Esquerda, transversal, dependente de pontos

$p$ ₀
À direita, os números podem ser bastante complexos, portanto, escolher a curva “auxiliar” corretamente é uma tarefa separada.

Agora que somos capazes de construir superfícies de filete para os casos elementares mais simples, podemos passar para um problema mais complexo: construir uma superfície para uma cadeia de faces.
O principal problema aqui é "costurar" superfícies adjacentes de maneira suave. Este é o quarto passo do algoritmo.

A dificuldade reside precisamente na suavidade da reticulação, uma vez que as superfícies são construídas com diferentes dados iniciais. Para garantir a suavidade, é necessário recorrer a vários truques: alterar a direção e o comprimento dos vetores de derivadas na direção longitudinal a uma certa distância da fronteira, alterar os valores das derivadas das funções de peso nas fronteiras, etc. Os resultados são visíveis na figura: as linhas mais suaves da zebra correspondem a uma superfície mais suave.

imagem

Acima está um modelo sem um algoritmo de suavização. Abaixo - após a aplicação do algoritmo.

Sumário

Como resultado de nossa pesquisa, o núcleo geométrico C3D é capaz de construir uma seção transversal de arredondamento, curvas de suporte e arredondamento de três faces; sabe como suavizar a superfície escolhendo uma parametrização; sabe parcialmente como unir superfícies de filete adjacentes sem problemas.

Autor - Anna Ladilova, Ph.D., matemático / programador C3D Labs

Modelagem geométrica de superfícies de filete

O que é arredondamento completo?

Algoritmo de arredondamento completo

Sumário

More articles: