Como a criptografia de curva elíptica funciona no TLS 1.3

Alguns alertas do leitor:

Para (de alguma forma) simplificar o processo de descrição e aumentar o volume do artigo que vamos escrever, é essencial fazer uma observação significativa e declarar a principal restrição imediatamente - tudo o que vamos dizer hoje sobre a prática O lado problemático é viável apenas em termos do TLS 1.3. Isso significa que, embora seu certificado ECDSA ainda funcione no TLS 1.2, se você desejar, fornecendo compatibilidade com versões anteriores, a descrição do processo real de handshake, roupas de cifra e benchmarks cliente-servidor abrange apenas o TLS 1.3. Obviamente, isso não está relacionado à descrição matemática de algoritmos por trás dos modernos sistemas de criptografia.

Este artigo não foi escrito por um matemático nem por um engenheiro - embora esses tenham ajudado a encontrar uma maneira de contornar a matemática assustadora e revido este artigo. Muito obrigado aos funcionários da Qrator Labs.

( C elve elíptico) D iffie- H ellman ( E phemeral)

O legado de Diffie - Hellman no século 21

Claro, isso não começou com Diffie nem Hellman. Mas, para fornecer uma linha do tempo correta, precisamos apontar datas e eventos principais.

Havia várias personas principais no desenvolvimento da criptografia moderna. Mais notavelmente, Alan Turing e Claud Shannon lançaram uma quantidade incrível de trabalho no campo da teoria da computação e teoria da informação, bem como da criptoanálise geral, e Diffie e Hellman são oficialmente creditados por terem a ideia de chave pública criptografia (ou assimétrica) (embora se saiba que no Reino Unido houve avanços sérios na criptografia que permaneceram em sigilo por muito tempo), tornando esses dois senhores pioneiros.

Em que exatamente?

Bem, isso pode parecer peculiar; no entanto, antes de 6 de novembro de 1976, não havia conhecimento público dos sistemas de criptografia de chave pública. Whitfield Diffie e Martin Hellman (e, de fato, Ralph Merkle) - matemáticos, engenheiros de computação e entusiastas, além de criptologistas, foram os primeiros.

Para aqueles que não estão cientes - devido ao papel que a análise de criptografia assumiu durante a Segunda Guerra Mundial e seu enorme impacto em manter as informações em segredo, os dois países que acreditavam ter o conhecimento mais avançado sobre criptografia - os EUA e o Reino Unido incluíram criptografia em suas listas de munições e utilizaram uma proibição pesada de exportação (enfraquecendo simultaneamente a implementação da criptografia para uso doméstico e comercial doméstico). Por esse motivo, os pesquisadores do Reino Unido que trabalham na técnica de troca de chaves assimétrica na sede de comunicações do governo e desenvolvem um esquema análogo não foram reconhecidos para esta invenção até 1997, quando as restrições aos algoritmos de criptografia e sua descrição se tornaram ineficazes.

Voltando aos nossos inventores duplos - o que Diffie e Hellman revolucionaram especificamente?

Vamos dar uma olhada no artigo original, ilustrando perfeitamente o grande salto que eles introduziram (mesmo teoricamente com o trabalho de pesquisa):

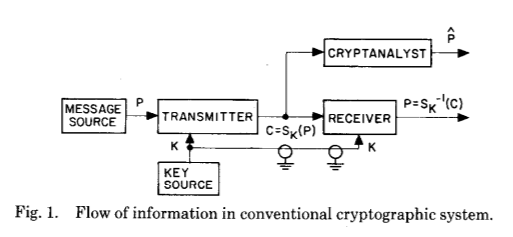
E o seguinte:

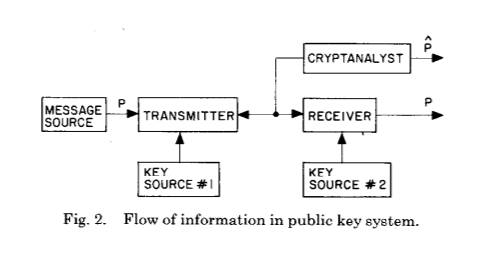
Essas duas figuras ilustram perfeitamente a enorme mudança que Whitfield Diffie e Martin Hellman introduziram após séculos de evolução na criptografia e criptografia - o estabelecimento de uma chave secreta compartilhada como resultado de uma computação criptográfica.

Vamos dar uma olhada em outra boa foto com cores:



Isso explica o que está acontecendo. Antes da invenção do contrato de chave de Diffie e Hellman, havia apenas uma chave simétrica - ela era usada para criptografar e descriptografar a mensagem. Se você deseja fornecer a alguém uma "chave", ela deve ser transferida por um canal "seguro". Você pode imaginar todas as restrições de um esquema de geração anterior imediatamente - você precisa de um canal seguro já estabelecido, não pode reutilizar a chave e, idealmente, o comprimento da chave deve ser o mesmo que o comprimento da mensagem.

Claude Shannon, em seu trabalho classificado em tempo de guerra, " Theory Communication of Secrecy Systems ", provou que todas as cifras teoricamente inquebráveis ​​devem ter os mesmos requisitos que a almofada de uso único - conhecida como cifra Vernam, pelo autor dessa cifra simétrica de fluxo polialfabético.

Mais uma vez, vamos dar uma olhada no artigo original:


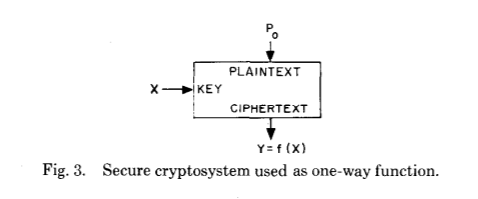
Antes de prosseguirmos, vamos nos perguntar - como dois, mesmo que brilhantes, no entanto, os seres humanos obtiveram uma melhoria tão significativa em um campo aplicado com essa história, especialmente em tempos de guerra?
Bem, por causa do:

• Teoria da informação , formulada por Claude Shannon;
• Teoria da computação influenciada, principalmente, por Alonzo Church, John von Neumann e Alan Turing;
• E, mais importante, a teoria da computabilidade baseada principalmente no trabalho de Turing, que poderíamos dizer que todos desenvolveram e amadureceram no mesmo período do século XX. Diffie e Hellman mencionaram Claude Shannon como o influenciador mais significativo de seu trabalho.

A “ Segurança Universal ” da Lenstra ilustra a quantidade de energia necessária para “quebrar” o sistema criptográfico simétrico com vários comprimentos de chave. Descobriu-se que a quebra de uma chave de curva elíptica de 228 bits exigiria a mesma quantidade de energia necessária para ferver toda a água da Terra. Porém, é válido apenas sob consideração de algoritmos e hardware conhecidos, pois, estritamente falando, ninguém sabe se existem algoritmos ou hardware significativamente mais eficientes. A chave CE de 228 bits é comparável à chave RSA de 2380 bits, mais sobre isso mais tarde. Embora nessa estimativa as chaves RSA e EC sejam usadas em um esquema de criptografia assimétrica, esses comprimentos de chave são um pouco equivalentes a uma chave de criptografia simétrica de 128 bits.

É fácil imaginar que algo "difícil de calcular" exigiria muita energia e / ou tempo necessário para o cálculo. Tendemos a pensar que os computadores podem "calcular tudo", mas acontece que isso não é verdade. Primeiro, existem exemplos indecidíveis, como o problema da parada, embora no campo da criptografia possamos evitar essa armadilha. Segundo, se considerarmos o tempo necessário para a execução de um determinado algoritmo, ele pode ser arbitrariamente alto. É isso que exploramos na criptografia. Um problema é considerado "fácil" para calcular se o tempo necessário para executar o respectivo algoritmo depende do tamanho da entrada (medido em bits) como um polinômio:$$ $ inline $ T (n) = O (n ^ k) $ inline $ , por alguma constante positiva$$ $ inline $ k $ inline $ . No campo da teoria da complexidade computacional , esses problemas formam a classe de complexidade P.

A classe de complexidade P é quase central, pois representa o problema para o qual existe um algoritmo de tempo polinomial determinístico. Outra classe de complexidade é a NP (os problemas que são "difíceis de calcular"), representando um conjunto de problemas de decisão, ou seja, problemas que exigem resposta "sim" ou "não", que têm uma prova verificável em tempo polinomial. Você vê a palavra "prova" aqui? É aí que chegamos às funções do alçapão, pertencentes à classe de complexidade NP.


Créditos: xkcd

Funções unidirecionais; Funções de alçapão

Por definição, uma função unidirecional é uma função que é fácil de calcular em todas as entradas, mas é difícil de reverter, ou seja, computa a entrada original apenas com a saída. "Fácil" e "difícil" se referem às definições da teoria da complexidade computacional acima. É interessante notar que a existência de funções unidirecionais não é (matematicamente) comprovada, porque sua existência provaria que as classes de complexidade P e NP não são iguais, enquanto P é igual a NP ou não é atualmente um problema em aberto. Portanto, lembre-se de que toda criptografia moderna se baseia em hipóteses não comprovadas.

Agora, em seu artigo original, Diffie e Hellman apresentam outra geração de funções unidirecionais que eles chamam de "funções de alçapão". Como eles diferem?
Como eles explicam em seu documento de referência:

Em um sistema de criptografia de chave pública, a codificação e decifração são governadas por chaves distintas, E e D, de modo que a computação de D a partir de E é computacionalmente inviável (por exemplo, exigir$$ $ inline $ 10 ^ {100} $ inline $ instruções). A chave de codificação E pode ser divulgada [em um diretório] sem comprometer a chave de decodificação D. Isso permite que qualquer usuário do sistema envie uma mensagem a qualquer outro usuário codificado de tal maneira que apenas o destinatário pretendido possa decifrá-la. .. O problema da autenticação é talvez uma barreira ainda mais séria à adoção universal de telecomunicações para transações comerciais do que os problemas de distribuição de chaves ... [ele] ... está no centro de qualquer sistema que envolva contratos e cobrança.

Por convenção, os caracteres de criptografia "Alice" e "Bob" (buscando comunicação segura) são freqüentemente usados ​​para explicar o conceito de chave pública. Alice e Bob concordam em números inteiros grandes$$ $ inline $ n $ inline $ e$$ $ inline $ g $ inline $ com$$ $ inline $ 1 <g <n $ inline $ . A seleção afeta a segurança do sistema. "O módulo$$ $ inline $ n $ inline $ deve ser primo; mais importante$$ $ inline $ (n-1) / 2 $ inline $ também deve ser um primo <...> e$$ $ inline $ g $ inline $ deve ser um módulo raiz primitivo$$ $ inline $ n $ inline $ <...> [e]$$ $ inline $ n $ inline $ deve ter pelo menos 512 bits. " O protocolo Diffie - Hellman pode ser declarado em forma elementar em 5 etapas.

1. Alice escolhe$$ $ inline $ x $ inline $ (um inteiro aleatório grande) e calcula$$ $ inline $ X = g ^ x \ bmod n $ inline $
2. Bob escolhe$$ $ inline $ y $ inline $ (um inteiro aleatório grande) e calcula$$ $ inline $ Y = g ^ y \ bmod n $ inline $
3. Alice envia$$ $ inline $ X $ inline $ para Bob, enquanto Bob envia$$ $ inline $ Y $ inline $ para Alice (eles mantêm$$ $ inline $ x $ inline $ e$$ $ inline $ y $ inline $ segredo um do outro)
4. Alice calcula$$ $ inline $ k = Y ^ x \ bmod n $ inline $
5. Bob calcula$$ $ inline $ k '= X ^ y \ bmod n $ inline $

Como resultado, Alice e Bob têm o mesmo valor$$ $ inline $ k = k '$ inline $ que serve como um segredo compartilhado.

A função Trapdoor é uma função unidirecional que possibilita encontrar sua inversa se houver uma informação especial chamada “trapdoor”. Parece fácil, embora tenha sido bastante difícil encontrar essas funções - o primeiro método viável foi encontrado na implementação de um algoritmo de criptografia assimétrica de criptografia de chave pública chamado RSA em homenagem a seus criadores: Ron Rivest, Adi Shamir e Leonard Adleman.

RSA

No RSA, a dureza de inverter a função é baseada no fato de que o fatorar (encontrar multiplicadores primos de um número) leva muito mais tempo que multiplicação, ou deveríamos dizer aqui que nenhum método de tempo polinomial para fatorar grandes números inteiros em um computador clássico tem foi encontrado, no entanto, não foi provado que não exista.

No RSA, como em qualquer outro sistema de criptografia de chave pública, existem duas chaves: pública e privada. O RSA pega a mensagem de entrada (representada como uma sequência de bits) e aplica uma operação matemática (módulo de exponenciação um grande número inteiro) para obter um resultado parecendo indistinguível aleatoriamente. A descriptografia obtém esse resultado e aplica uma operação semelhante para retornar a mensagem original. Na criptografia assimétrica, a criptografia é feita com a chave pública e descriptografada com a privada.

Como Porque os operandos pertencem a um grupo cíclico finito (um conjunto de números inteiros com multiplicação na aritmética modular). Os computadores não lidam muito bem com números arbitrariamente grandes, mas, felizmente, nosso grupo cíclico de números inteiros é executar uma operação chamada “envolver” - um número maior que o máximo permitido é envolvido em um número no intervalo válido em que operamos . Isso nos permite operar com teclas de comprimento "não superior a". Na criptografia de curva elíptica, também são usados ​​grupos cíclicos (multiplicativos), mas construídos de maneira um pouco diferente, como veremos mais adiante.

Basicamente, o que a RSA faz é pegar dois números primos grandes e multiplicá-los para obter o chamado módulo. Todos os outros números a serem tratados residem entre zero e o módulo. O módulo deve fazer parte da chave pública e seu comprimento de bit determina o comprimento da chave. A segunda parte da chave pública é um número escolhido entre zero e o totiente de Euler (a implementação moderna do RSA toma o totient de Carmichael em vez do de Euler) do módulo com algumas restrições adicionais. Finalmente, a chave privada deve ser calculada resolvendo-se alguma equação modular. Para criptografar um número, simplesmente aumentamos para a potência igual à chave pública e, para decriptografar um número, aumentamos para a potência igual à chave privada. Graças à natureza cíclica do grupo, recuperamos o número inicial.

Atualmente, existem dois problemas significativos com a RSA, sendo uma conseqüência da outra. À medida que o comprimento de uma chave (ou seja, o número de bits) aumenta, o fator de complexidade cresce não tão rápido quanto se pode esperar. Isso ocorre porque existe um algoritmo de fatoração subexponencial (mas ainda super polinomial ). Portanto, para manter um nível de segurança apropriado, o comprimento da chave RSA precisa crescer um pouco mais rápido que o comprimento da chave ECC. É por isso que a maioria das chaves RSA difundidas atualmente tem 2048 ou 3072 bits.

Um pouco mais tarde, veremos em números como o comprimento da chave afeta a eficiência geral do sistema de criptografia comparando o certificado RSA e ECDSA assinado com a autoridade Let's Encrypt.

( C elve elíptico) Ignorância digital S Algoritmo

A busca por uma melhor função de alçapão acabou levando os criptografistas a uma evolução ativa no ramo da matemática em meados dos anos 80, dedicado às curvas elípticas.

Seria a tarefa final descrever a criptografia de curva elíptica em um artigo, portanto não o faremos. Em vez disso, vamos dar uma olhada em uma função de alçapão de curva elíptica com base no problema de logaritmo discreto.

Existem muitos iniciadores e introduções mais aprofundadas da criptografia de curva elíptica, e recomendamos especialmente o “ECC: uma introdução suave” de Andrea Corbellini, se você estiver interessado em matemática.

O que nos interessa são parâmetros bastante "simples".

A curva elíptica é definida por uma equação como esta:$$ $ inline $ y ^ 2 = x ^ 3 + ax + b $ inline $
Essa curva é necessária para construir um subgrupo cíclico sobre um campo finito. Portanto, os seguintes parâmetros estão sendo usados:

• O principal$$ $ inline $ p $ inline $ que especifica o tamanho do campo finito;
• Os coeficientes$$ $ inline $ a $ inline $ e$$ $ inline $ b $ inline $ da equação da curva elíptica;
• O ponto base$$ $ inline $ g $ inline $ que gera o subgrupo mencionado;
• A ordem$$ $ inline $ n $ inline $ do subgrupo;
• O cofator$$ $ inline $ h $ inline $ do subgrupo.

Em conclusão, os parâmetros de domínio para nossos algoritmos é o sextuplet$$ $ inline $ (p, a, b, G, n, h) $ inline $ .
Tais curvas elípticas funcionam sobre o campo finito$$ $ inline $ \ mathbb {F} _p $ inline $ onde$$ $ inline $ p $ inline $ é um número primo bastante grande. Então, nós temos um conjunto de módulos inteiros$$ $ inline $ p $ inline $ , em que operações como adição, subtração, multiplicação, inverso aditivo e inverso multiplicativo são possíveis. A adição e a multiplicação funcionam de maneira semelhante à aritmética modular ou denominada “relógio” que vimos nas “voltas” da RSA.
Como a curva é simétrica em relação ao eixo x, dado qualquer ponto$$ $ inline $ P $ inline $ , podemos pegar$$ $ inline $ −P $ inline $ para ser o ponto oposto a ele. Tomamos$$ $ inline $ −O $ inline $ ser apenas$$ $ inline $ O $ inline $ .
A adição de pontos de curva é definida de maneira que dados pontos$$ $ inline $ P $ inline $ e$$ $ inline $ Q $ inline $ , podemos desenhar uma linha que cruza esses pontos e a curva de interseção em um terceiro ponto$$ $ inline $ R $ inline $ para que$$ $ inline $ P + Q = -R $ inline $ e$$ $ inline $ P + Q + R = 0 $ inline $ .

Vamos dar uma olhada na explicação de Marc Hughes :

Uma linha de inclinação constante que viaja ao longo da superfície do toro é mostrada acima. Essa linha passa por dois pontos inteiros selecionados aleatoriamente na curva.



Para adicionar dois pontos no gráfico, desenhe uma linha a partir do primeiro ponto selecionado$$ $ inline $ P $ inline $ para o segundo ponto selecionado$$ $ inline $ Q $ inline $ e estenda a linha até cruzar outro ponto no gráfico$$ $ inline $ -R $ inline $ , estendendo-o além dos limites da plotagem, se necessário.

Depois de interceptar um ponto inteiro, reflita o ponto verticalmente no meio do gráfico (uma linha pontilhada laranja) para encontrar o novo ponto$$ $ inline $ R $ inline $ no gráfico Portanto,$$ $ inline $ P + Q = R $ inline $ .

A multiplicação por um escalar agora é trivial:$$ $ inline $ n \ cdot P = P + P + P + \ pontos + P $ inline $ (aqui estão$$ $ inline $ n $ inline $ summands).

A função alçapão aqui está no problema do logaritmo discreto (para curvas elípticas), não na fatoração que analisamos na seção RSA. O problema é: se sabemos$$ $ inline $ P $ inline $ e$$ $ inline $ Q $ inline $ , o que é tal$$ $ inline $ k $ inline $ que$$ $ inline $ Q = k \ cdot P $ inline $ ?

Supõe-se que tanto o problema de fatoração (subjacente ao RSA) quanto o logaritmo discreto para curvas elípticas (que é a base do ECDSA e ECDH) sejam difíceis, ou seja, não há algoritmos conhecidos para resolver esse problema no tempo polinomial de uma determinada chave comprimento.

Enquanto, normalmente, qualquer pessoa ficaria envergonhada por misturar o ECDH (Troca de Chaves) com o algoritmo de assinatura (ECDSA), precisamos explicar como eles trabalham juntos. Um certificado TLS moderno contém uma chave pública, no nosso caso, do par de chaves gerado pelo algoritmo de curva elíptica, geralmente assinado por uma autoridade de nível superior. O cliente verifica a assinatura do servidor e obtém o segredo compartilhado. O segredo compartilhado é usado em um algoritmo de criptografia simétrica, como AES ou ChaCha20. No entanto, o princípio permanece o mesmo: concorde com os parâmetros do domínio (o sextuplet), obtenha o par de chaves, onde a chave privada é um número inteiro selecionado aleatoriamente (o multiplicando de$$ $ inline $ Q = k \ cdot P $ inline $ ) e a chave pública é um ponto na curva. Algoritmos de assinatura usam o ponto base$$ $ inline $ g $ inline $ , que é um gerador para um subgrupo de grande ordem principal$$ $ inline $ n $ inline $ , de modo que$$ $ inline $ n \ cdot G = 0 $ inline $ , onde 0 é o elemento de identidade. A assinatura prova que a conexão segura está sendo estabelecida com a parte autêntica - um servidor que possui o certificado TLS (chave pública) assinado por alguma autoridade de certificação para o nome do servidor especificado.

(EC) DH (E) + ECDSA = Forma atual do handshake

No TLS moderno (1.3), o cliente e o servidor geram seu par de chaves público-privado em tempo real, enquanto estabelecem a conexão, isso é chamado de versão efêmera da troca de chaves. As bibliotecas TLS do navegador mais populares suportam isso. Eles usam principalmente a curva elíptica Edwards 25519 , apresentada por Daniel J. Bernstein (djb), oferecendo segurança de 128 bits. Desde 2014, o openssh usa essa curva para a criação do par de chaves. Em 2019, porém, os navegadores ainda não suportam sessões TLS com servidores com um certificado com chave pública EdDSA.

Mas vamos voltar a como as coisas funcionam no final de 2019 com o TLS 1.3.

Os principais mecanismos de troca no TLS 1.3 são restritos a (EC) DH (E) (com o x25519 é o suportado nas bibliotecas TLS do lado do cliente dos navegadores mais populares, bem como nas bibliotecas TLS do lado do servidor, como OpenSSL, que examinaremos um pouco mais tarde) e a lista de conjuntos de criptografia contém apenas três entradas: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 e TLS_CHACHA20_POLY1305_SHA256. Para aqueles que sabem como os conjuntos de cifras foram nomeados na versão TLS 1.2, é evidente imediatamente que o mecanismo de troca de chaves agora está "desanexado" do nome do conjunto de cifras, também os modos de troca estático RSA e estático Diffie - Hellman removidos inteiramente da especificação. Até a retomada da sessão com base no PSK é feita sobre ECDHE no TLS 1.3. Isso também se aplica aos parâmetros DH personalizados, que não são permitidos agora, deixando apenas aqueles geralmente aceitos como seguros na especificação final do protocolo.

É interessante que exista uma diferença bastante significativa em como os algoritmos de criptografia assimétrica funcionam atualmente. Com o ECC (e os certificados ECDSA em particular), usamos chaves menores para obter níveis "convenientes" de segurança, em comparação com o RSA. Isso permite o uso de um algoritmo de criptografia assimétrica mais forte e mecanismos de troca de chaves em dispositivos menores e, às vezes, até em coisas que geralmente não são consideradas um dispositivo (cartão inteligente).

Antes de tudo, é necessário mencionar o que “sistema de criptografia híbrido” significa em termos do TLS 1.3.
Um sistema de criptografia híbrido é aquele que usa criptografia assimétrica (chave pública) para estabelecer um segredo compartilhado, que é usado ainda mais como chave em um fluxo simétrico ou em uma cifra de bloco.

Em segundo lugar, infraestrutura e certificados de chave pública. É interessante que, em sua entrevista de 2004, Martin Hellman mencionou um "herói não reconhecido" Loren Kohnfelder, cuja tese de bacharel no MIT introduziu uma estrutura em árvore do que hoje conhecemos como infraestrutura de chave pública. No entanto, vamos reverter para certificados.

O fato de o servidor realmente possuir a chave privada é garantido por sua assinatura, que pode ser verificada com a chave pública do servidor. E o certificado garante que alguma chave pública pertença a um servidor específico. Isso significa que você está estabelecendo uma comunicação segura com a parte específica e não com um impostor. Seu banco, não um cibercriminoso. No TLS 1.3, há uma melhoria significativa em relação ao formato de negociação anterior - o servidor assina todas as informações que possui até o momento: o cliente Olá e o Servidor Olá, incluindo a cifra negociada. Vamos dar uma olhada na seção correspondente da RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

No TLS 1.3, o cliente envia o compartilhamento de chave (junto com os parâmetros necessários), algoritmos de assinatura imediatamente na primeira mensagem (Client Hello). As chaves necessárias para trocar com o servidor são criadas em segundo plano, sem que o usuário perceba esse fato. Eles são trocados ainda com o servidor para criar um segredo comum, a partir de chaves secretas pré-mestre que foram estabelecidas quando o servidor enviou sua mensagem (Server Hello) respondendo ao cliente.
No lado “Server Hello”, você pode ver o Certificado * sendo transferido para o cliente, junto com a parte Verificação de Certificado *, que verifica se a parte possui a chave privada para a entrada de chave pública correspondente e cria a chave de sessão (simétrica) se tudo corre como planejado - o que significa que o lado que solicitou os dados (cliente) verificou com êxito o lado de resposta (servidor), criando ainda um segredo comum.

Existem duas operações essenciais ocultas nessas transmissões - criação e verificação de assinaturas. Essas são feitas nos dois lados da comunicação, uma vez que a “assinatura” é essencialmente uma prova de que a parte realmente possui a chave privada correspondente à chave pública, que os dados são do signatário e que a mensagem não foi alterada em trânsito.

Com a RSA, como veremos mais adiante, a operação de assinatura é a mais cara. Como estamos assinando com uma chave longa de 2048 ou 3072 bits, essa operação carrega o servidor significativamente, muito mais do que o cliente que verifica essa assinatura.

Com o ECDSA, temos chaves menores (veremos o ECDSA com o NIST P-256 (ou o secp256v1)), mas com operações mais complexas. Como resultado, ele pode ser visto como o RSA “invertido” - o cliente é carregado mais, pelo cálculo da verificação de assinatura, enquanto o servidor lida facilmente com a criação da assinatura. As medições verificam isso, consulte a seção "Um pouco de referência".

Esse efeito dimensiona facilmente a Internet atualmente - já que os clientes modernos são quase igualmente poderosos como os servidores (levando em conta apenas a frequência de núcleo da CPU), para que possam efetivamente levar a operação cara a descoberto. O servidor, por sua vez, pode usar os recursos liberados para criar mais assinaturas e estabelecer mais sessões.

Vamos criptografar a assinatura do certificado

Portanto, para fornecer ao leitor algumas instruções práticas e práticas sobre como criar um servidor habilitado para TLS com o par de chaves ECDSA assinado pela autoridade Let's Encrypt, decidimos ilustrar um processo completo de criação de um par de chaves necessário criar um CSR (solicitação de assinatura de certificado) para o Let's Encrypt e, como resultado, obter o certificado ECDSA necessário para o nosso servidor.

Temos que gerar uma chave privada para continuar. Usaremos a biblioteca OpenSSL.
O manual do OpenSSL descreve a geração de qualquer chave EC por meio de um comando especial, designado especialmente para o ramo da curva elíptica do algoritmo de geração.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Para verificar se a biblioteca OpenSSL fez tudo certo, podemos executar o comando ec .

 openssl ec -in privatekey.pem -noout -text 

A saída nos mostrará a curva especificada com a qual a chave foi criada.

O próximo passo é essencial para a criação do CSR - para pular o processo de preenchimento de todos os detalhes de informações necessárias para obter o certificado, precisamos do arquivo de configuração. Felizmente, a Mozilla fez todo o trabalho por nós, introduzindo o " SSL Configuration Generator ". Lá, você pode escolher entre qualquer opção de servidor disponível. A configuração pura do OpenSSL, peculiarmente não presente na página do gerador, seria algo como isto:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Nota: não é necessário ter o CNF - caso contrário, você deverá preencher esses detalhes na linha de comando.

Agora, siga a criação de um próprio CSR. Aqui temos um prático comando OpenSSL.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

Também podemos verificar a correção de um CSR recém-criado.

 openssl req -in csr.pem -noout -text -verify 

Aqui chegamos à fase final - usando um cliente ACME, certbot, para passar nossa solicitação de assinatura de certificado para Let's Encrypt.

O Certbot ajuda você a obter o certificado necessário e tem várias opções. Dito isso, se você é novo na criptografia de chave pública e na infraestrutura de PKI que temos em 2019, é melhor usar --dry-run antes de tentar obter o certificado para qualquer domínio seu.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

Nesse caso, o cliente certbot verifica se a lista de domínios solicitados (na linha de comandos) corresponde aos domínios listados na solicitação de assinatura de certificado. No comando --dns-somednsprovider é uma mentira, porque existem várias maneiras de você provar que o Let's Encrypt está de posse de uma parte específica do tráfego da Internet. No entanto, se você estiver usando algum provedor de hospedagem em nuvem pública, digamos DigitalOcean, Hetzner, Amazon, Azure, qualquer coisa - provavelmente haveria uma maneira mais natural de fornecer as informações necessárias, porque seu provedor já fez alguma ferramenta de integração.

Depois, se tiver certeza da exatidão dos parâmetros que você está usando ao passar seu CSR para o Let's Encrypt via um cliente certbot - exclua o parâmetro --dry-run do seu comando e continue.

Se for bem-sucedido, o cliente produzirá vários certificados como saída: o próprio certificado assinado, as certificações raiz e intermediária e a combinação deste último como a cadeia de certificados com o último nome, tudo no formato de arquivo .pem.

O OpenSSL possui um comando que poderíamos usar para inspecionar os certificados:

 openssl x509 -in chainfilepath.pem -noout -text 

Nesse momento, fica evidente que o Let's Encrypt assinou o certificado usando o resumo SHA256. Além disso, a assinatura de raiz e intermediários do ECDSA se enquadra na seção "Próximos recursos", o que significa efetivamente que, no momento, você obteria apenas intermediários do RSA. Mas tudo bem, pois você ainda está usando a chave pública ECDSA.

No final desta seção, gostaríamos de dizer algo relacionado ao comprimento das chaves. Na segurança da informação, é comum dizer que o nível de segurança é 2 ^ x, onde x é o tamanho do bit (o RSA é uma exceção aqui, pois cresce um pouco mais lentamente do que exponencialmente). Para aproximar como as chaves usadas para diferentes algoritmos se correspondem, consultaríamos a página wiki do OpenSSL.
Como você pode ver, as diferenças são bastante proeminentes. Embora com o Let's Encrypt não possamos obter nenhum certificado assinado fora das chaves da curva elíptica 256 (secp256v1) e 384 (secp384r1).

Problemas e exceções conhecidos, e a NSA

Créditos: xkcd

Provavelmente, a questão central do uso da criptografia de curva elíptica ao longo dos anos foi a necessidade de um gerador de números aleatórios cuidadosamente criado, a fim de criar chaves do nível de segurança necessário.

Houve um escândalo maciço em torno do algoritmo Dual_EC_DRBG (gerador de bit aleatório determinístico de curva elíptica), que levou muitos anos para ser resolvido. Além disso, há incerteza em torno das patentes da ECC, pois é sabido que muitas delas pertenciam à empresa Certicom, que foi adquirida pela Blackberry. Também existem empresas que são certificadas pelo uso do ECC da Blackberry. Certamente, existe uma simples desconfiança em alguns padrões do NIST, que podem ou não ser afetados pela NSA ou por qualquer outra instituição de fiscalização e fiscalização dos Estados Unidos.

O lado da implementação de um problema é uma questão totalmente diferente. Em 2010, o console PlayStation 3 sofreu uma recuperação de chave privada da Sony devido à implementação inadequada do algoritmo ECDSA - eles tinham um aleatório estático que tornava a função do alçapão solucionável. O OpenSSL também sofreu no ano seguinte, no entanto, corrigindo rapidamente a vulnerabilidade que permitia a recuperação de uma chave privada com a ajuda de um ataque de tempo, para obter mais informações, consulte o artigo original .

Em 2013, na conferência da RSA, um grupo de pesquisadores apresentou sua “ falha aleatória! Artigo sobre vulnerabilidades da classe Java SecureRandom. Meio ano depois, ele chegou às carteiras do Bitcoin Android , criadas usando PRNG criptograficamente seguro.

Devido a sérias vulnerabilidades seriais descobertas, no mesmo mês de agosto de 2013, a IETF lançou uma RFC 6979 , descrevendo uma geração determinística de k usada na criação da chave. Poderíamos dizer que essa medida corrigiu o problema, mas não o iremos - a qualquer momento os pesquisadores poderão encontrar problemas em várias implementações devido a um desvio desnecessário das especificações do protocolo.

Sobre a NSA. Se você não ouviu falar da história do Dual_EC_DRBG - reserve um tempo e leia os artigos correspondentes, não se arrependerá de entrar em detalhes. Edward Snowden faz parte dessa história porque as revelações de 2013 provaram as suspeitas anteriores. Isso resultou em muitos criptógrafos proeminentes perdendo a confiança no NIST desde que a organização projetou e descreveu muitas das curvas e algoritmos adicionais subjacentes ao ECDSA.

A curva 25519 de Daniel Bernstein e a função DH são a resposta para esses dois problemas e, como descrevemos anteriormente, a transição para o EdDSA é lenta, embora evidente. Mesmo com as curvas do NIST, nenhuma evidência de sua vulnerabilidade foi encontrada ainda e, como já mencionamos, a experiência relacionada ao acaso tem sido bastante instrutiva.

Para concluir esta parte, queremos citar John von Neumann: "Qualquer pessoa que tente gerar números aleatórios por meios determinísticos está, é claro, vivendo em estado de pecado".

Um pouco de referência

Usamos um servidor NGINX 1.16.0 com OpenSSL 1.1.1d para executar esses benchmarks com vários certificados. Como mencionamos anteriormente, atualmente o Let's Encrypt permite apenas os algoritmos prime256v1 e secp384r1 para solicitações de assinatura de certificados e não fornece certificados ECDSA raiz e intermediários, provavelmente trabalhando nesse recurso no momento em que escrevemos este artigo.
Como você pode ver, para um único núcleo da CPU Intel® Xeon® Silver 4114 a 2,20GHz (lançado no terceiro trimestre de 17), a diferença geral no desempenho do ECDSA, em comparação com o amplamente adotado RSA 2048 é de 3,5x.

Agora, vamos dar uma olhada nos resultados de velocidade OpenSSL do mesmo processador com ECDSA e RSA.
Aqui podemos ver uma confirmação da tese anterior de diferentes custos computacionais para as operações de sinalização e verificação do ECC e RSA. Como resultado, atualmente equipado com TLS 1.3 ECC fornece um aumento significativo no desempenho no nível de segurança de bit mais alto, comparado com o RSA. Essa é a razão mais substancial pela qual nós, na Qrator Labs, incentivamos nossos clientes a adotar a ECDSA. Com as CPUs modernas, você obtém quase a diferença de 5x em favor da ECDSA.

Se você estiver interessado em saber como sua CPU executa cálculos criptográficos, você pode executar um simples comando openssl speed . Os -rsa , -ecdsa e -eddsa forneceriam resultados de referência para os algoritmos de assinatura correspondentes.

(Sobreposto) Futuro

Créditos: djb

É irônico que enquanto estávamos preparando este artigo, o Google anunciou " alcançar a supremacia quântica ". Isso significa que estamos em perigo agora e tudo o que foi desenvolvido até esse momento não fornece segredo?

Bem, não.

Como Bruce Schneier escreveu em seu ensaio para a IEEE Security and Privacy " Criptografia após as terras alienígenas ", um enorme golpe com um computador quântico poderoso o suficiente poderia ser causado à criptografia de chave pública (assimétrica). A criptografia simétrica ainda seria forte.

Queremos citar Bruce Schneier com o seguinte:

Há mais um cenário futuro a considerar, que não requer um computador quântico. Embora existam várias teorias matemáticas que sustentam a via única que usamos na criptografia, provar que a validade dessas teorias é de fato um dos grandes problemas em aberto na ciência da computação. Assim como é possível para um criptografador inteligente encontrar um novo truque que facilita a quebra de um algoritmo específico, podemos imaginar alienígenas com teoria matemática suficiente para quebrar todos os algoritmos de criptografia. Para nós, hoje, isso é ridículo. A criptografia de chave pública é toda teoria dos números e potencialmente vulnerável a alienígenas com maior inclinação matemática. A criptografia simétrica é tanta confusão não-linear, tão fácil de tornar mais complexa e tão fácil de aumentar o comprimento da chave, que esse futuro é inimaginável. Considere uma variante AES com um tamanho de bloco e chave de 512 bits e 128 rodadas. A menos que a matemática seja fundamentalmente diferente da nossa compreensão atual, isso estará seguro até que os computadores sejam feitos de algo que não seja matéria e ocupem algo que não seja o espaço.

Mas se o inimaginável acontecer, isso nos deixaria com criptografia baseada apenas na teoria da informação: blocos únicos e suas variantes.

Essa é a área em que, exceto procurando falhas de implementação, a maioria dos problemas pode ser encontrada. Se houver um grupo de matemáticos bem financiados, criptoanalistas / criptografadores e engenheiros de computação trabalhando para provar ou refutar alguns problemas matemáticos complexos extraordinários (como P? = NP) e obter resultados substanciais até esse momento, podemos estar com problemas. No entanto, é improvável que tais avanços nas ciências da computação, nas teorias da informação e da computabilidade ocorram, pois esse fato escreveria os nomes de seus criadores nas páginas da History e, especificamente, dos livros de História da Internet, que não têm preço para quem é inteligente. . Portanto, esse cenário pode ser considerado quase impossível.

Não está claro se, nos próximos 5 anos, haveria algum sucesso com a computação quântica, embora já existam várias primitivas de criptografia consideradas adequadas para o mundo pós-quântico: treliças, curvas elípticas supersingulares baseadas em isogenia, hashes e códigos. Por enquanto, os especialistas em segurança estão apenas experimentando com eles. No entanto, não há dúvida de que, no caso de uma necessidade, a humanidade empregaria rapidamente tais algoritmos em escala de massa.

Por enquanto, a criptografia baseada em curva elíptica parece se encaixar perfeitamente na década futura, fornecendo segurança e desempenho.