Como a criptografia de curva elíptica funciona no TLS 1.3

Alguns avisos ao leitor:

Para (o máximo possível) simplificar o processo de explicação e reduzir o volume da publicação, vale a pena fazer uma reserva importante imediatamente - tudo o que escrevemos sobre o lado prático da questão está correto para o protocolo TLS versão 1.3. Isso significa que, embora seu certificado ECDSA funcione, se desejado, com o TLS 1.2, a descrição do processo de handshake, conjuntos de códigos e benchmarks é feita com base na versão mais recente do protocolo TLS - 1.3. Como você sabe, isso não se aplica à descrição matemática dos algoritmos subjacentes à fundação dos sistemas criptográficos modernos.

Este material não foi escrito por um matemático ou mesmo por um engenheiro - embora eles tenham ajudado a abrir caminho na selva matemática. Muito obrigado à equipe do Qrator Labs.

( C elve elíptico) D iffie- H ellman ( E phemeral)

Legado Diffie-Hellman do século XXI

Naturalmente, esse tópico não começa com Whitfield Diffie e nem com Martin Hellman. Alan Turing e Claude Shannon fizeram uma enorme contribuição para a teoria dos algoritmos e da teoria da informação, bem como para o campo da criptoanálise. Diffie e Hellman, por sua vez, são oficialmente reconhecidos pelos autores da idéia de criptografia de chave pública (também chamada de assimétrica) - embora agora seja sabido que resultados sérios nessa área também foram alcançados no Reino Unido. No entanto, eles permaneceram em segredo por um longo tempo - o que torna os dois cavalheiros mencionados nos pioneiros em legendas.

O que exatamente?

Isso pode parecer engraçado, mas até 6 de novembro de 1976, não havia conhecimento disponível sobre os sistemas criptográficos de chave pública. Whitfield Diffie e Martin Hellman (e, de fato, Ralph Merkle) - matemáticos, engenheiros de computação e entusiastas, além de criptologistas, foram os primeiros a propor um conceito adequado.

Durante a Segunda Guerra Mundial, a criptografia ajudou a manter as informações em segredo, e a criptoanálise ajudou a divulgá-las. Os Estados Unidos e o Reino Unido se consideravam os mais avançados no campo da criptografia. Esses dois países incluíram algoritmos criptográficos na seção de armas e vetaram suas exportações. Ao mesmo tempo, a criptografia disponível e destinada ao uso comercial ou doméstico foi reduzida nesses países. Por esse motivo, os pesquisadores britânicos que trabalhavam em um esquema de distribuição de chaves assimétricas no Centro de Comunicações do Governo (GCHQ) e desenvolviam um conceito semelhante não foram reconhecidos pela comunidade até 1997, quando as restrições existentes nos algoritmos criptográficos e em sua descrição perderam todo o significado e, em geral, moralmente desatualizado.

Voltando ao nosso par de inventores - o que exatamente Diffie e Hellman revolucionaram?

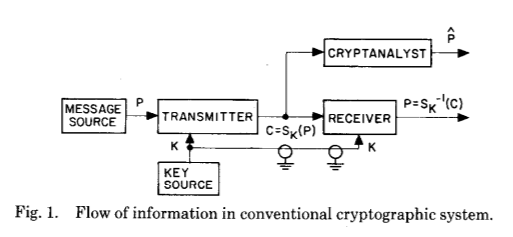
Para explicar isso, vamos dar uma olhada na ilustração da publicação original, que reflete perfeitamente o salto gigantesco na compreensão de como a criptografia pode funcionar - mesmo que apenas inicialmente teoricamente:

E agora, para o seguinte:

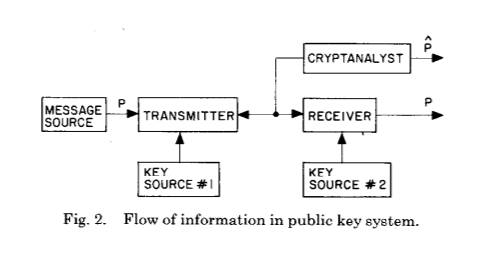
Essas duas imagens mostram a principal inovação de Whitfield Diffie e Martin Hellman após séculos de desenvolvimento de criptografia e criptoanálise - o estabelecimento de um segredo comum como resultado de cálculos de um determinado tipo.

Vejamos outra foto da Wikipedia, onde cores diferentes são usadas como segredos:



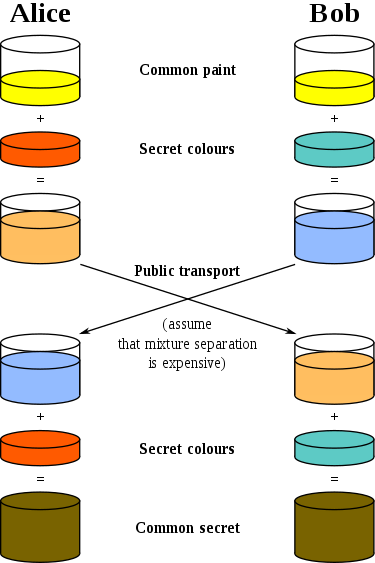
Ela também explica bem o que está acontecendo. Antes da inovação de Diffie e Hellman, havia apenas uma chave comum na forma de um esquema de estabelecimento de chave comum - era usado para criptografar e descriptografar uma mensagem. Se você deseja transferir essa chave para o segundo lado, ela deve ser transmitida pelo canal originalmente protegido. Todas as limitações desse esquema ficam imediatamente claras - você precisa de um canal de comunicação seguro (de escuta), não pode usar a mesma chave mais de uma vez e, idealmente, o tamanho da chave deve corresponder ao tamanho da mensagem.

Claude Shannon, em seu trabalho posteriormente desclassificado, "Teoria da comunicação em sistemas secretos", provou que todas as cifras teoricamente inquebráveis ​​deveriam ter as mesmas propriedades que um bloco de cifra único - também conhecido como cifra Vernam, pelo nome do criador desse algoritmo de criptografia de fluxo polialfabético aditivo.

E, novamente, vamos dar uma olhada na publicação científica original:


Antes de prosseguirmos, vamos nos perguntar uma pergunta obviamente simples - como duas pessoas, mesmo muito desenvolvidas intelectualmente, conseguiram algo tão inovador no campo aplicado, especialmente considerando os enormes sucessos da guerra? Provavelmente devido à combinação das seguintes áreas que estavam se desenvolvendo ativamente:

• Teoria da Informação Formulada por Claude Shannon;
• Teoria do algoritmo , que foi influenciada, entre outros, por Alonzo Church, John von Neumann e Alan Turing;
• E, acima de tudo, a teoria da computabilidade , baseada principalmente no trabalho de Turing.

Podemos dizer que todas essas áreas se desenvolveram e amadureceram no mesmo período do século XX. Diffie e Hellman também mencionaram Claude Shannon como uma figura que influenciou seu trabalho mais do que outros.

O conceito de "Segurança Universal" de Arjen Lenstra mostra quanta energia precisa ser gasta em "invadir" um sistema de criptografia simétrico com chaves de diferentes comprimentos. Descobriu-se que, para decifrar a chave de 228 bits do algoritmo com base em curvas elípticas, você precisa de energia suficiente para aquecer toda a água da Terra até o ponto de ebulição. No entanto, essa afirmação está correta apenas se considerarmos algoritmos conhecidos e usarmos equipamentos modernos, uma vez que, estritamente falando, algoritmos ou equipamentos mais eficientes são possíveis, mas sua existência ainda não é conhecida. A chave de 228 bits do algoritmo EC para complexidade de hackers é comparável à chave de 2380 bits do RSA, mas mais sobre isso posteriormente. Nesta comparação, as chaves RSA e EC são usadas em um sistema de criptografia assimétrico, elas podem ser consideradas equivalentes a uma chave de 128 bits em um esquema simétrico.

É fácil imaginar que algo “difícil de calcular” exigirá uma grande quantidade de tempo e energia para ser calculado. Tendemos a pensar que os computadores podem "contar tudo", mas acontece que isso está longe da verdade.

Em primeiro lugar, existem exemplos de problemas insolúveis, como o problema de parada. No entanto, no campo da criptografia, essas tarefas não são usadas.

Em segundo lugar, se considerarmos o tempo de execução exigido por um algoritmo específico, ele pode ser arbitrariamente grande. É exatamente isso que a criptografia usa. Uma tarefa é considerada computacionalmente "simples" se o tempo necessário para o algoritmo correspondente funcionar depende do tamanho dos dados de entrada (medidos em bits) como um polinômio: $$$T (n) = O (n ^ k)$para algum positivo $$$k$. Na teoria da complexidade computacional, esses problemas formam uma classe de complexidade P. Se o tempo de execução do algoritmo cresce mais rápido que um polinômio, por exemplo, exponencialmente, essa tarefa é considerada computacionalmente “difícil”.

A classe de complexidade P inclui tarefas para as quais existe um algoritmo determinístico que funciona em tempo polinomial. Outra classe de complexidade é a NP (na qual, presumivelmente, existem problemas "difíceis"), que é um problema de solvabilidade - ou seja, um problema que exige uma resposta "sim" ou "não", cuja correção da solução pode ser verificada - ou seja, para fornecer prova da correção da solução - em tempo polinomial. Veja a palavra "prova" aqui? Este é o local em que passamos para funções unilaterais, cujo problema de inversão pertence à classe de complexidade NP.


Postada por: xkcd

(Funções unidirecionais (com entrada secreta))

Por definição, uma função unidirecional é uma função fácil de calcular para qualquer entrada, mas difícil de inverter, ou seja, obter a entrada original apenas com o resultado. "Fácil" e "difícil" se referem à teoria da complexidade computacional mencionada acima. É interessante que a existência de funções unidirecionais (matematicamente) não tenha sido comprovada, pois uma prova rigorosa de sua existência também provaria a desigualdade das classes P e NP, um dos problemas do milênio e um problema aberto urgente, cuja solução promete uma descoberta algorítmica. Portanto, é necessário ter em mente que quase toda criptografia moderna se baseia em hipóteses não comprovadas.

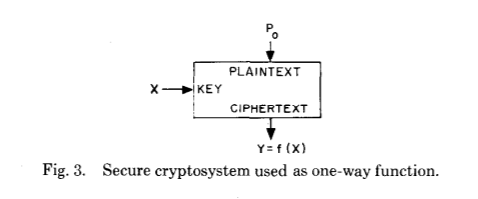
Em sua publicação original, Diffie e Hellman apresentam uma nova geração de funções unidirecionais, chamando-as de "funções unidirecionais com uma entrada secreta" - na função de alçapão em inglês. Como eles diferem das funções unidirecionais?

Vejamos a explicação original deles:

Em um sistema de criptografia com uma chave pública, a criptografia e a descriptografia são executadas por várias chaves - E e D, respectivamente, de modo que a computação de D a partir de E é praticamente impossível (por exemplo, exigir $$$10 ^ {100}$instruções). A chave de criptografia E pode ser divulgada publicamente sem comprometer a chave D. Isso permite que qualquer usuário do sistema envie uma mensagem a qualquer outro usuário, criptografado de forma que apenas o destinatário esperado possa descriptografá-la. <...> A tarefa de autenticação, talvez, é um problema de telecomunicações mais sério para transações comerciais, em comparação com a distribuição de chaves, pois é a autenticação que está no coração de qualquer sistema que trabalha com contratos e cobrança por pagamento.

Geralmente, os caracteres criptográficos Alice e Bob são usados ​​para explicar os princípios da operação do sistema de criptografia (eles se esforçam para obter uma comunicação segura). Alice e Bob concordam em escolher números primos grandes $$$n$e $$$g$tal que $$$1 <g <n$. Essa escolha afeta a segurança de todo o circuito. Número $$$n$chamado módulo deve ser simples; além disso, o número $$$(n-1) / 2$também deve ser simples, mas $$$g$deve ser a raiz primitiva no grupo de resíduos módulo $$$n$; além $$$n$deve ser grande o suficiente - pelo menos 512 bits em representação binária. Além disso, o protocolo Diffie-Hellman pode ser descrito em cinco etapas simples:

1. Alice escolhe $$$x$(grande prime) e calcula $$$X = g ^ x \ bmod n$
2. Bob picks $$$y$(também um grande primo) e calcula $$$Y = g ^ y \ bmod n$
3. Alice envia $$$X$Bob, Bob envia $$$Y$Alice ( $$$x$e $$$y$cada um deles permanece em segredo)
4. Alice calcula $$$k = Y ^ x \ bmod n$
5. Bob está calculando $$$k '= X ^ y \ bmod n$

Como resultado, Alice e Bob obtêm o mesmo resultado na construção. $$$k = k '$- um segredo compartilhado.

Portanto, uma função unidirecional com uma entrada secreta é uma função unidirecional que pode ser revertida com uma informação especial chamada de "entrada secreta". Parece simples, mas na prática, encontrar essa função acabou sendo uma tarefa não trivial - o primeiro método decente acabou por ser o progenitor de toda uma família de algoritmos baseados em uma chave pública chamada RSA pelos nomes de seus criadores: Ron Rivesta, Adi Shamira e Leonard Adleman.

RSA

No RSA, a complexidade de inverter uma função é baseada no fato de que a fatoração (fatoração de um número) leva muito mais tempo do que a multiplicação ou, mais precisamente, pode-se argumentar que nenhum método para fatorar grandes números em tempo polinomial foi encontrado em um computador clássico, embora não fosse Está provado que tal algoritmo não pode existir.

No RSA, como em qualquer outro sistema criptográfico com uma chave pública, existem duas chaves: pública e privada. O algoritmo RSA pega uma mensagem de entrada representada por uma sequência de bits e aplica uma operação matemática (aumentando para um módulo de potência um número grande) para obter um resultado indistinguível aleatoriamente. Para descriptografia, o resultado é obtido e uma operação semelhante é executada para receber a mensagem original. Na criptografia assimétrica, a criptografia é realizada com uma chave pública e a descriptografia com uma chave privada.

Como isso é possível? Devido ao fato de os valores utilizados pertencerem a um grupo cíclico finito (o conjunto de números inteiros com multiplicação na aritmética modular). Os computadores não funcionam muito bem com números arbitrariamente grandes, mas a propriedade do grupo cíclico é "contornada" - um número maior que o máximo permitido é "envolto" em um valor do conjunto permitido. Isso nos permite usar chaves com um comprimento "não superior a" um certo número de bits. Na criptografia baseada em curvas elípticas, grupos cíclicos (multiplicativos) também são usados, mas são construídos de maneira um pouco diferente, como veremos mais adiante.

Em um nível muito primitivo, tudo o que o RSA faz é pegar dois primos grandes, multiplicando-os para obter o chamado módulo. Todos os outros números com os quais as operações serão executadas devem estar entre zero e o valor do módulo. O próprio módulo se tornará parte da chave pública - seu comprimento determina o comprimento da chave. A segunda parte da chave pública é o número escolhido entre zero e o valor da função Euler (implementações modernas de RSA usam a função Carmichael em vez de Euler) do módulo, com algumas restrições adicionais. Por fim, você pode calcular a chave privada resolvendo a equação modular. Para criptografar a mensagem, pegamos o número que representa a mensagem e simplesmente aumentamos para a potência igual ao valor da chave pública e descriptografamos - para receber a mensagem original, aumentamos para a potência igual ao valor da chave privada. Devido à natureza cíclica do grupo, obtemos o mesmo significado.

Hoje, a RSA tem dois problemas principais, um dos quais é consequência do outro. À medida que o comprimento da chave aumenta, a complexidade não cresce tão rápido quanto gostaríamos. Isso ocorre porque existe um algoritmo de fatoração subexponencial (mas ainda superpolinomial ). Portanto, para manter o nível de proteção necessário, o comprimento da chave RSA deve crescer um pouco mais rápido que o da chave ECC. Por esse motivo, os comprimentos de chave RSA mais comuns atualmente são bastante grandes: 2048 e 3072 bits.

Um pouco mais tarde, veremos em figuras específicas como o tamanho da chave afeta o desempenho final do sistema de criptografia comparando os certificados assinados pelo Let's Encrypt RSA e ECDSA.

C elabora elíptica Digital igoritmos

Em busca de funções mais confiáveis ​​com uma entrada secreta, em meados dos anos 80, os criptografadores passaram a usar um ramo da matemática dedicado às curvas elípticas.

Seria muito difícil descrever todos os detalhes da criptografia com base nas curvas elípticas em um texto, portanto não faremos isso. Em vez disso, vejamos uma função de entrada secreta unidirecional construída com base em curvas elípticas e no problema de logaritmo discreto.

Há um grande número de materiais de revisão e introduções mais detalhadas para essa área de criptografia. Gostaríamos de destacar “ECC: uma introdução suave” de Andrea Corbellini, especialmente se você estiver interessado no dispositivo.

Nós, neste material, estamos interessados ​​em uma explicação muito mais "simples".
Uma curva elíptica é definida por uma equação que se parece com isso: $$$y ^ 2 = x ^ 3 + ax + b$.

O segundo objeto é um subgrupo cíclico sobre um campo finito. Os seguintes parâmetros são usados ​​no algoritmo ECC:

• Número primo $$$p$, que determina a dimensão do campo final;
• Odds $$$a$e $$$b$equações da curva elíptica;
• Ponto base $$$G$gerar o subgrupo já mencionado;
• Encomendar $$$n$subgrupos;
• Cofactor $$$h$subgrupos.

Como resultado, o conjunto de parâmetros para nossos algoritmos é representado por seis $$$(p, a, b, G, n, h)$.

Os pontos de uma curva elíptica pertencem a um campo finito $$$\ mathbb {F} _p$onde $$$p$este é um número primo bastante grande. Então, nós temos muitos módulos inteiros $$$p$onde operações como adição, subtração, multiplicação, tomando o oposto são possíveis. A adição e a multiplicação funcionam de maneira semelhante à que descrevemos em termos da aritmética modular da seção RSA (wrap-around).

Como a curva é simétrica em relação ao eixo x, para qualquer ponto $$$P$nós podemos pegar $$$−P$e obtenha o ponto oposto a ele. Nós imediatamente estipulamos que o ponto $$$−O$corresponde a zero, ou seja, $$$−O$vai ser simples $$$O$.

A adição de pontos em uma curva é definida para que, conhecendo os pontos $$$P$e $$$Q$, podemos desenhar uma linha que passa por esses dois pontos e também por um terceiro - $$$R$para que $$$P + Q = -R$e $$$P + Q + R = 0$.

Vamos dar uma olhada na ilustração ilustrada de Mark Hughes :

Vemos uma linha reta esticada ao longo da superfície do toro. A linha cruza dois pontos selecionados aleatoriamente na curva.



Para encontrar $$$R$, desenhamos uma linha a partir do primeiro ponto selecionado $$$P$para o segundo $$$Q$continuando a linha até cruzar a curva no terceiro ponto $$$-R$.

Após a interseção, reflita o ponto relativo ao eixo da abcissa para encontrar o ponto $$$R$.

A multiplicação por um escalar é determinada obviamente: $$$n \ cdot P = P + P + P + \ pontos + P$.

A função unidirecional com uma entrada secreta nesse caso depende do problema discreto do logaritmo para curvas elípticas, e não da fatoração, como é o caso da RSA. O problema do logaritmo discreto nesse caso é formulado da seguinte forma: se conhecido $$$P$e $$$Q$, então como encontrar $$$k$tal que $$$Q = k \ cdot P$?

Tanto o problema de fatoração (RSA subjacente) quanto o logaritmo discreto para curvas elípticas (que são a base do ECDSA e ECDH) são considerados difíceis - em outras palavras, não há algoritmos para resolver esses problemas em tempo polinomial para um determinado comprimento de chave.

Embora, normalmente, eu fosse bombardeado com trapos sujos (na melhor das hipóteses) por misturar algoritmos de distribuição de assinatura (ECDH) com assinatura (ECDSA), ainda tenho que explicar como eles funcionam juntos.Um certificado TLS moderno contém uma chave pública, no nosso caso, de um par gerado usando um algoritmo baseado em curvas elípticas, geralmente assinado por alguma organização autorizada. O cliente verifica a assinatura do servidor e gera um segredo compartilhado. Esse segredo é usado em um algoritmo de criptografia simétrica como AES ou ChaCha20. Entretanto, os princípios básicos permanecem os mesmos: concordar com um conjunto (seis) de parâmetros, obter um par de chaves, em que a chave privada é um número inteiro selecionado aleatoriamente (um fator de$$ ), e a chave pública é um ponto na curva. Algoritmos de assinatura usam um ponto base$Q=k\cdot P$$$ , que é um gerador de um subgrupo de ordem$G$$$$n$ ( $$é um primo grande), então$n$$$ , onde 0 é o elemento neutro do grupo. A assinatura prova que uma conexão segura é estabelecida com uma parte autenticada - um servidor que possui um certificado TLS (chave pública) assinado por uma organização autorizada para um determinado nome de servidor.$n\cdot G=0$

(EC) DH (E) + ECDSA = Forma moderna de aperto de mão

No TLS moderno versão 1.3, o cliente e o servidor geram um par de chaves rapidamente, estabelecendo uma conexão. Isso é chamado de versão "efêmera" do algoritmo de troca de chaves. As bibliotecas TLS mais populares suportam exatamente essa versão de protocolo. Na maioria das vezes, a curva elíptica Edwards 25519 , proposta por Daniel Bernstein Jr. (djb), que fornece um nível de proteção de 128 bits , é usada hoje . Desde 2014, essa curva está disponível para a criação de pares de chaves na biblioteca openssh. No entanto, a partir do final de 2019, os navegadores ainda não estabelecem uma sessão TLS com servidores usando a chave pública para o algoritmo de assinatura EdDSA.

Vamos ver como tudo funciona no TLS 1.3.

Na versão mais recente do protocolo, os mecanismos de distribuição de chaves são limitados a (EC) DH (E) - x25519 é a função mais comum para obter uma chave compartilhada - é suportado pela maioria das bibliotecas TLS de navegadores e servidores. O conjunto de criptografia consiste em apenas três entradas: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 e TLS_CHACHA20_POLY1305_SHA256. Para aqueles que estão familiarizados com como os conjuntos de códigos foram nomeados na versão anterior do protocolo - TLS 1.2, é óbvio que a indicação do mecanismo de troca de chaves foi "separada" do conjunto de códigos durante a transição para o TLS 1.3. Além disso, os métodos estáticos de troca de chaves RSA e DH foram descartados da especificação. Mesmo a recuperação da sessão no TLS 1.3 com a ajuda do PSK e os tickets da sessão anterior ocorrem de acordo com o protocolo ECDHE, onde a última efemeridade E é especialmente importante.Além disso, no TLS 1.3, não é possível definir seus próprios valores para o mecanismo Diffie-Hellman - apenas um conjunto predefinido é deixado nas especificações do protocolo, há um consenso em relação à segurança desse conjunto.

De particular interesse é o fato de que os modernos mecanismos de criptografia assimétrica funcionam de maneira diferente. No ECC (em particular, ao usar certificados ECDSA), usamos chaves de tamanho relativamente curto em comparação com o RSA para obter níveis aceitáveis ​​de segurança. Isso permite que você use criptografia assimétrica forte e esquemas de troca de chaves, mesmo em dispositivos que, ao que parece, não devem ter energia suficiente para as operações necessárias - por exemplo, cartões inteligentes.

Em primeiro lugar, é necessário esclarecer o significado do termo "sistema de criptografia híbrido", que se aplica à descrição do TLS 1.3. O sistema de criptografia híbrido usa um esquema de criptografia assimétrico (com uma chave pública) para estabelecer um segredo compartilhado, que é usado como chave em um algoritmo de criptografia de bloco ou fluxo simétrico.

Em segundo lugar, existe uma infraestrutura de chaves públicas (PKI) e certificados (CA). É interessante que em 2004 Martin Hellman tenha mencionado um dos “heróis desconhecidos” - Lauren Könfelder, cuja tese para defender o diploma de bacharel do MIT era a possibilidade de criar uma estrutura em árvore - o que hoje conhecemos como PKI. Mas vamos voltar aos certificados.

O fato de o servidor realmente possuir a chave privada é verificado por sua assinatura, que pode ser verificada usando a chave pública. E o arquivo de certificado no servidor certifica que uma chave pública específica pertence a um servidor específico. Isso significa que você está estabelecendo uma conexão segura com o interlocutor desejado, e não um impostor - seu banco, não uma fraude cibernética.

O TLS 1.3 melhorou significativamente o esquema de negociação em comparação com as versões anteriores do protocolo. Agora, o servidor assina todas as informações recebidas no handshake no momento da criação dessa assinatura: hello cliente e hello servidor próprio, juntamente com um conjunto de cifras selecionadas para uso. Vamos dar uma olhada na seção correspondente da descrição da interação do RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

No TLS 1.3, o cliente envia sua parte da chave (junto com os parâmetros necessários) e a lista de assinaturas disponíveis na primeira mensagem (Client Hello). As chaves necessárias nesta fase são criadas pelo cliente em tempo real - o usuário nem percebe isso. Em seguida, o cliente e o servidor trocam essas informações para criar um segredo comum - uma chave de sessão criada (ou, mais precisamente, derivada) do par pré-mestre recebido após o servidor responder ao cliente com sua mensagem (Server Hello).
No lado "Server Hello", é possível ver o registro correspondente à transferência do certificado para o cliente (Certificado *), junto com a verificação CertificateVerify *, que confirma que a parte realmente possui uma chave privada relacionada ao registro de chave pública correspondente e, em seguida, cria um par de chaves (simétrico) em caso de sucesso. Em outras palavras, a parte solicitante de dados (cliente) verificou com êxito a autenticidade da parte respondente (servidor) mudando para o uso de um segredo compartilhado.

As duas operações criptográficas principais são protegidas nessa transferência - criando uma assinatura e verificando a assinatura. Essas operações geralmente são executadas em extremidades diferentes da conexão, pois os clientes geralmente verificam a autenticidade do servidor. A assinatura é essencialmente uma confirmação da propriedade da chave privada correspondente à chave pública. Ou seja, recebemos dados do signatário e garantimos que a mensagem não foi alterada durante a transferência.

Ao usar o algoritmo RSA, como demonstraremos mais adiante sobre os números, a operação de criação de uma assinatura é a mais cara. Como assinamos com uma chave de 2048 ou 3072 bits, essa operação carrega significativamente o servidor - muito mais forte que o cliente durante a verificação (de assinatura).

No ECDSA, operamos com chaves relativamente curtas (no exemplo de benchmark, veremos o ECDSA usando a curva NIST P-256 (ou secp256v1), mas essas chaves estão envolvidas em operações mais complexas. Como resultado, o uso do ECC pode ser representado como um RSA "invertido" com pontos de vista de desempenho: o cliente é muito mais carregado com a operação de verificação de assinatura, enquanto o servidor lida facilmente com a operação de criação de assinatura, conforme evidenciado pelas medições que fornecemos na seção de benchmark.

Esse efeito ajuda a dimensionar a Internet - como os clientes modernos são quase tão poderosos quanto os servidores (se considerarmos apenas a velocidade do clock do núcleo do processador), eles podem efetivamente assumir uma operação computacionalmente difícil sem problemas. O servidor, por sua vez, pode usar o poder de computação liberado para criar mais assinaturas e, como resultado, estabelecer mais sessões.

Assinatura de certificado em Let's Encrypt

Forneceremos ao leitor uma instrução simples e compreensível na qual você pode criar independentemente um servidor capaz de estabelecer uma sessão TLS usando um par de chaves ECDSA no qual Let's Encrypt é publicamente assinado e está incluído no certificado de cadeia de confiança como certificado.
Decidimos mostrar o caminho completo da criação de chaves, criando uma solicitação de assinatura de certificado (CSR) para Let's Encrypt e enviando-a para assinatura usando o utilitário certbot, que retorna as cadeias necessárias e o próprio certificado ECDSA.

Primeiro você precisa criar um par de chaves. Para isso, usaremos a biblioteca OpenSSL. O Guia do Usuário do OpenSSL diz que a criação de chaves para algoritmos baseados em curvas elípticas ocorre usando um comando especial dedicado à família de algoritmos baseados em curvas elípticas.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Para verificar se nossa equipe funcionou corretamente, executamos o comando ec indicando o caminho para o arquivo recém-criado que contém a chave privada.

 openssl ec -in privatekey.pem -noout -text 

A saída deve nos mostrar a curva usada, com a qual a chave foi gerada.

O próximo passo é muito importante ao criar um CSR - para não preencher o questionário necessário para assinar um certificado todas as vezes, precisamos de um arquivo de configuração. Felizmente, quase todo o trabalho para nós foi realizado pela Mozilla, criando o " SSL Configuration Generator ". Nele, você pode escolher entre uma variedade de opções para modos de servidor com os quais pode estabelecer uma conexão TLS. A configuração limpa do OpenSSL, por algum motivo ausente no gerador Mozilla, fica assim:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Nota: você não precisa ter um arquivo de configuração - se não estiver lá, será solicitado que você preencha todos os campos na linha de comando. Com o arquivo de configuração, o caminho para o qual especificamos no próximo comando, o processo é simplificado.

A seguir, é criada a própria solicitação de assinatura de certificado (CSR). Para isso, temos uma equipe OpenSSL conveniente.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

Também podemos verificar a correção do CSR recém-criado.

 openssl req -in csr.pem -noout -text -verify 

Finalmente, chegamos ao estágio final - usando o cliente ACME, certbot, transferiremos nossa solicitação para assinar o certificado da organização Let's Encrypt.

O Certbot não apenas ajudará você a obter um certificado, mas também possui muitas outras ótimas opções. Acrescentamos que, se você é novo na criptografia com uma chave pública e realmente não entende a infraestrutura de chave pública existente no momento, é melhor usar a opção --dry-run antes de tentar obter um certificado real para qualquer um dos seus domínios.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

Nesse caso, o cliente certbot verifica se a lista de domínios solicitados solicitados na linha de comandos corresponde à lista na solicitação de assinatura de certificado (CSR). Dentro da --dns-somednsprovider pouco, pois existem várias maneiras de confirmar o Let's Encrypt que você possui uma determinada porção do tráfego da Internet. Mas se você usar algum tipo de provedor de nuvem, como DigitalOcean, AWS, Azure, Hetzner, o que for - você já pode ter uma maneira mais fácil de fornecer as informações necessárias para a certificação, porque seu provedor cuidou da ferramenta de integração.

Depois disso, se você tiver certeza de que os parâmetros passados ​​para o CSR usando o certbot para Let's Encrypt estão corretos, remova o parâmetro --dry-run do comando e continue.

Se for bem-sucedido, o cliente retornará vários certificados: o certificado assinado em si, os certificados intermediário e raiz, bem como uma combinação deste último na forma de uma cadeia de certificados, tudo no formato .pem.

O OpenSSL possui um comando que usamos para olhar dentro do certificado:

 openssl x509 -in chainfilepath.pem -noout -text 

Agora deve ficar claro que o Let's Encrypt assinou o certificado usando o algoritmo de hash SHA256. Além disso, o Let's Encrypt está planejando adicionar assinaturas raiz e intermediárias ao ECDSA, portanto, por enquanto, ainda resta conteúdo das assinaturas intermediárias RSA. Mas não é assustador, porque, de qualquer forma, você usará a chave pública da ECDSA.

No final desta seção, gostaríamos de adicionar algumas informações sobre a comparação dos comprimentos de chave de vários algoritmos. Na segurança da informação, é habitual dizer que o nível de segurança é 2 ^ x, onde x é o tamanho do bit (RSA é uma exceção, pois cresce um pouco mais lentamente que o expoente). Para aproximar como as chaves de vários algoritmos são comparadas, consultamos a página wiki do OpenSSL :

Como você pode ver, as diferenças são visíveis. Embora, por enquanto, o Let's Encrypt permita receber certificados assinados apenas nas chaves de apenas duas curvas elípticas - 256 (secp256v1) e 384 (secp384r1).

Dificuldades conhecidas, bem como a NSA

Postada por: xkcd

Talvez o problema central no uso de criptografia baseada em curvas elípticas tenha sido a necessidade de um gerador de números aleatórios muito bem implementado, necessário para criar chaves de um determinado nível de segurança.

Um enorme escândalo foi associado ao algoritmo Dual_EC_DRBG - levou muitos anos para resolvê-lo. Há incerteza sobre a base de patentes em torno do ECC - sabe-se que muitas patentes pertenciam à Certicom, que foi adquirida pela Blackberry. Existem também vários casos de certificação Blackberry ECC conhecidos. Finalmente, existe uma certa desconfiança dos padrões do NIST, que pode ser influenciada pela NSA ou por qualquer outra agência de inteligência dos EUA.

Erros na implementação de padrões criptográficos são um tópico completamente ortogonal. Em 2010, o PlayStation 3 sofreu um vazamento da chave privada da Sony devido à implementação incorreta do algoritmo ECDSA - a Sony não conseguiu lidar com o RNG e forneceu o mesmo número aleatório, o que tornou possível resolver a função com uma entrada secreta. O OpenSSL sofreu no ano seguinte, no entanto, rapidamente corrigiu uma vulnerabilidade que permitia obter uma chave privada usando um ataque de tempo - mais detalhes podem ser encontrados na publicação original da pesquisa .

Em uma conferência da RSA em 2013, um grupo de pesquisadores apresentou um trabalho de pesquisa intitulado “ Randomly Failed! ”Dedicado às vulnerabilidades da classe Java SecureRandom. Seis meses depois, tudo começou com as carteiras Bitcoin criadas usando um gerador de números pseudo-aleatórios criptograficamente inseguros.

Devido ao fato de várias vulnerabilidades sérias terem sido descobertas em um curto período de tempo, no mesmo mês de agosto de 2013, a IETF lançou o RFC 6979 , que descreve a geração determinística de k ao criar uma chave. Poderíamos escrever que o problema foi resolvido dessa maneira, mas não iremos - a qualquer momento, os pesquisadores poderão encontrar novos erros na implementação devido a desvios desnecessários das especificações do protocolo.

E algumas palavras sobre a NSA. Se você não conhece o histórico do Dual_EC_DRBG - reserve algum tempo e leia os materiais relevantes, não se arrependerá de ter descoberto os detalhes. Edward Snowden se tornou parte dessa história, porque foi por causa de seus vazamentos em 2013 que todas as dúvidas que existiam foram confirmadas. Isso resultou no fato de que muitos criptografistas eminentes perderam a confiança no NIST, pois foi essa organização que criou e descreveu muitas das curvas e algoritmos elípticos que funcionam no ECDSA.

A curva 25519, de autoria de Daniel Burnshite, e a função Diffie-Hellman para distribuição de chaves, é a resposta para muitas das perguntas acima. E, como já escrevemos, há um movimento constante em direção à EdDSA. No caso das curvas do NIST, ainda não foi encontrada confirmação de sua vulnerabilidade e, quanto à experiência com números aleatórios, foi bastante doloroso e contribuiu para a rápida assimilação.

Para concluir esta parte, gostaríamos de citar John von Neumann: "Qualquer um que tenha uma fraqueza nos métodos aritméticos para obter números aleatórios está sem pecado além de qualquer dúvida".

Alguns benchmarks

Usamos o servidor NGINX 1.16.0 com a biblioteca OpenSSL versão 1.1.1d para realizar testes com dois certificados. Como mencionado anteriormente, no momento, o Let's Encrypt permite que você use apenas os algoritmos prime256v1 e secp384r1 para criar uma solicitação de assinatura de certificado, além de não fornecer certificados raiz e intermediários com uma assinatura ECDSA, provavelmente lidando com esse recurso enquanto estiver lendo esta nota.

Como você pode ver, em um único núcleo da CPU Intel® Xeon® Silver 4114 a 2,20GHz (lançado no terceiro trimestre de 17), a diferença total entre o desempenho do ECDSA e o RSA geralmente aceito com um comprimento de chave de 2048 bits é 3,5 vezes.

Vejamos os resultados da execução do comando openssl -speed para ECDSA e RSA no mesmo processador.

Aqui podemos encontrar a confirmação de uma tese escrita anteriormente sobre como as operações computacionais de uma assinatura e sua verificação diferem entre ECC e RSA. Atualmente, armada com TLS 1.3, a criptografia baseada em curvas elípticas proporciona um aumento significativo no desempenho do servidor com um nível mais alto de proteção em comparação com o RSA. Essa é a principal razão pela qual nós, da Qrator Labs, recomendamos e incentivamos fortemente os clientes que também estão prontos para usar os certificados ECDSA. Nas CPUs modernas, o ganho de desempenho em favor da ECDSA é de 5x.

Se você estiver interessado em como o processador (doméstico ou servidor) lida com a computação criptográfica, execute o comando openssl speed. As -rsa , -ecdsa e -eddsa permitem especificar os algoritmos de interesse para o benchmarking.

O futuro (em superposição)

Ironicamente, no processo de redação deste material, o Google anunciou "alcançar superioridade quântica" . Isso significa que já estamos em perigo e todo o progresso feito no momento atual não é mais capaz de garantir sigilo?

Não.

Como Bruce Schneier escreveu no ensaio “Criptografia após Alien Landing” para a Circular IEEE de Segurança e Privacidade, um computador quântico pode realmente causar um golpe sério apenas na criptografia assimétrica com uma chave pública. Algoritmos simétricos permanecerão persistentes.

Mas, para continuar, passaremos a palavra ao próprio Sr. Schneier:

Há outro cenário futuro que não requer um computador quântico. Embora agora tenhamos várias teorias matemáticas subjacentes à unilateralidade usada na criptografia, a prova da validade dessas teorias é na verdade um dos maiores problemas em aberto na ciência da computação. Assim como um criptógrafo inteligente pode encontrar um novo truque que facilita a invasão de um algoritmo específico, podemos imaginar alienígenas com teoria matemática suficiente para quebrar todos os algoritmos de criptografia. Hoje parece ridículo. A criptografia de chave pública é uma teoria dos números e é potencialmente vulnerável a alienígenas preocupados com a matemática. A criptografia simétrica é tão não linear, tão simples de criar e complicar, e também como é fácil alongar chaves, que futuro é inimaginável. Um exemplo é a variante AES com um tamanho de bloco e chave de 512 bits, além de 128 rodadas. Se a matemática não é fundamentalmente diferente da nossa compreensão atual, esse algoritmo estará seguro até que os computadores sejam feitos de algo que não seja matéria e ocupem algo que não seja o espaço.

Mas se o inimaginável acontecer, ele nos deixará apenas com criptografia baseada apenas na teoria da informação: blocos de notas cifradas descartáveis ​​e suas variantes.

Bruce Schneier descreve perfeitamente a área em que, além dos erros de implementação, podem ser encontradas as principais vulnerabilidades da criptografia moderna. Se em algum lugar houver um grupo de matemáticos, criptoanalistas e criptografistas abastados, juntamente com engenheiros de computação trabalhando na prova ou refutação de alguns problemas matemáticos particularmente complexos (como P? = NP), que conseguiram alcançar algum progresso nessa atividade no momento - nossa posição é vulnerável. Ao rejeitar as teorias da conspiração, pode-se dizer que esse progresso nos campos da ciência da computação, teoria da informação e teoria da computabilidade dificilmente pode ser oculto. Tal evento teria inserido os nomes de seus próprios criadores nas páginas da História e, em particular, nos livros didáticos da História da Internet, que são inestimáveis ​​para qualquer indivíduo ou grupo tão inteligente. Portanto, um cenário semelhante pode ser descartado como impossível.

Também não está claro se tais sucessos na computação quântica serão alcançados nos próximos 5 anos - e já existem primitivas criptográficas adequadas para uso no mundo pós-quântico: treliças, usando isogenização supersingular de curvas elípticas, funções de hash, códigos de correção de erros. Agora, os especialistas em segurança estão apenas experimentando com eles, mas não há dúvida de que, se necessário, a humanidade encontrará uma maneira de implantar rapidamente novos algoritmos em qualquer escala.

Resta acrescentar que, para a próxima década, a criptografia baseada em curvas elípticas parece ser ideal para as metas e necessidades que a maioria de seus usuários estabelece para si, fornecendo segurança e alto desempenho.