Tetris como uma impressora

Girando, reorganizando e abaixando uma sequência predeterminada de formas, o Tetris Printer Algorithm usa a mecânica do Tetris para gerar bitmaps arbitrários.

Descrição do algoritmo

O algoritmo converte os pixels da imagem de origem nos quadrados do campo Tetris linha por linha, movendo-se de baixo para cima. Para gerar um único quadrado, o algoritmo monta uma estrutura que consiste em uma área retangular que é completamente suportada por um quadrado abaixo dele. Após a montagem da região retangular, suas linhas são limpas, deixando um quadrado embaixo dela. Aqui estão três exemplos desse comportamento.




Como mostrado abaixo, o algoritmo também pode gerar vários quadrados com uma estrutura.


No processo de construção de uma linha, todos os quadrados criados dessa maneira devem se basear em algo. Nas imagens mostradas acima, os quadrados gerados estão no chão do campo de jogo. No entanto, se uma linha arbitrária contiver furos, ela não poderá fornecer o suporte necessário para construir uma linha acima dela. O algoritmo resolve esse problema criando uma plataforma plana no topo da string com furos. Na animação abaixo, uma plataforma construída em cima de uma linha consiste em um quadrado vermelho. Uma plataforma é uma estrutura temporária e a inserção da última forma a remove.


A linha de 5 quadrados vermelhos mostrada abaixo está no topo da linha de 3 quadrados vermelhos. Isso é realizado através da construção de uma plataforma plana no topo da linha de fundo. A plataforma fornece o suporte necessário para gerar 5 quadrados vermelhos. No final, a plataforma é excluída inserindo a última forma e a nova linha se encaixa. Observe que, se o algoritmo precisar gerar linhas na ordem inversa (uma linha de 3 quadrados vermelhos acima de uma linha de 5 quadrados vermelhos), a plataforma não será necessária.

Padrões de um quadrado

Para referência, darei os nomes de 7 tetramino (peças do jogo).


A versão do algoritmo de impressora Tetris apresentada no artigo foi projetada especificamente para renderizar sprites de videogames antigos. Esses jogos incluíam gráficos em blocos 8 × 8 e 2 bytes foram alocados para cada pixel. Portanto, os sprites geralmente continham apenas 3 cores mais áreas transparentes e, na maioria das vezes, tinham um tamanho de 16 × 16 ou 16 × 32 pixels.

A animação abaixo mostra todos os padrões usados ​​para criar quadrados individuais. Cada padrão usa o tetramino intercambiável J, T e L, criando um único quadrado na parte inferior. O algoritmo atribui esse tetramino a uma das três cores presentes no sprite. O restante do tetramino recebe cores arbitrárias. Durante a jogabilidade, todas as cores permanecem constantes.


Devido à forma dos três tetraminos, é impossível criar um quadrado a partir das três cores nas duas primeiras e nas duas últimas colunas. Portanto, a largura mínima do campo de jogo para renderizar um sprite com uma largura de 16 pixels é 2 + 16 + 2 = 20 quadrados. No entanto, descobriu-se que 20 é muito pouco.

Como mostrado abaixo, a área acima do quadrado inferior único não pode consistir em apenas uma linha, porque as únicas figuras que podem caber nele (tetramino I) não têm suporte.


Com duas linhas, a única maneira de ampliar todo o campo de jogo para que ele tenha suporte é usar o tetramino S e Z. Mas, neste caso, os furos permanecerão na linha superior.


O número mínimo de linhas necessárias acima do quadrado inferior é 3 e, como mostrado várias vezes acima, esses padrões existem. 20 quadrados é a largura mínima necessária para colocar um sprite com uma largura de 16 pixels. Mas 20 × 3 + 1 = 61, e esse número não é divisível por 4, o que significa que não pode ser construído a partir do tetramino. No entanto, uma largura de 21 nos dá 21 × 3 + 1 = 64, e pode ser construída a partir de 16 tetramino. De fato, essa largura permite ao algoritmo renderizar sprites com até 17 pixels de largura.

O campo de jogo do Tetris original tem um tamanho de 10 × 20 quadrados (proporção 1: 2). Nesta versão do algoritmo, essa proporção é preservada - o campo de jogo tem um tamanho de 21 × 42 quadrados.

Como o tetramino J, T e L são intercambiáveis ​​ao criar um quadrado, e 3 quadrados desses tetraminos estão envolvidos na criação de uma linha acima dele, existem 21 - 3 = 18 padrões para criar um único quadrado. No entanto, devido à simetria espelhada, existem apenas 9. Existem três linhas que funcionam para a maioria delas 9. No entanto, um estudo aprofundado em computador mostrou que os dois padrões precisavam de mais. A próxima opção possível é 7 linhas, porque 21 × 7 + 1 = 148, o que requer 37 tetraminos. Como mostrado nas imagens abaixo, esses padrões existem.

Vários padrões quadrados

Os padrões para criar vários quadrados são limitados às mesmas três cores criadas pelos padrões de um único quadrado. Os quadrados resultantes são criados a partir do tetramino J, T e L, cada um dos quais ocupa 3 quadrados em uma linha acima da linha de criação. O número máximo de quadrados que podem ser potencialmente criados com um único padrão é 21/3 = 7. No entanto, para sprites com uma largura de 16 pixels, o tetramino mais à direita não pode criar um quadrado. Mesmo no caso de sprites com uma largura de 17 pixels, ele pode criar um quadrado de apenas uma cor. Portanto, o padrão de criação de 7 quadrados raramente é usado.


O número de padrões para criar um número arbitrário de quadrados pode ser determinado usando a combinação de enumerações. Considere o padrão abaixo, representando uma linha acima de uma linha de três quadrados. Cada bloco de três quadrados brancos adjacentes designa uma parte do tetramino; quadrados criados não são mostrados.


Três tetraminos criam 4 espaços vazios. Existem 21 - 3 × 3 = 12 quadrados escuros que podem ser arbitrariamente inseridos nesses espaços vazios para formar um padrão específico. O número de maneiras de distribuir esses quadrados escuros pode ser calculado colocando-os em uma linha na qual quadrados brancos únicos são tratados como divisores.


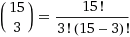
Portanto, a tarefa foi reduzida ao cálculo do valor do coeficiente do polinômio. Observando esses quadrados em branco, você pode entender que essa é uma questão de várias maneiras de escolher 3 de 15. = 455

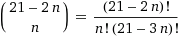
No caso geral, para n é igual a . Mas, devido à simetria espelhada, de fato, são metade disso; se a quantidade for ímpar, dividindo por dois, arredondamos para o número inteiro mais próximo para incluir nele um padrão perfeitamente simétrico que deveria existir nesse conjunto, como, por exemplo, mostrado abaixo para o caso 455.


Aplicando esta fórmula ao 7 tetramino, confirmamos o óbvio: existe apenas um padrão para criar 7 quadrados.

O padrão de criação de 6 quadrados pode ser construído de duas maneiras: duas linhas preenchidas (2 × 21 + 6 = 48) e seis linhas preenchidas (6 × 21 + 6 = 132), o que requer 12 e 33 tetramino. A fórmula acima mostra que existem 84 padrões para a criação de 6 quadrados, mas apenas 35 deles podem ser construídos a partir de 2 linhas completas. 49 padrões requerem 6 linhas. Os números são ímpares devido aos padrões simétricos mostrados abaixo.



Também é importante notar que duas linhas são possíveis aqui, porque, ao contrário do padrão de criação de um quadrado que exigia o tetramino S e Z, 6 figuras são usadas nesses padrões.

A tabela abaixo mostra o número de quadrados criados por cada tipo de padrão, o número de linhas completas, o número de tetramino usado e o número de padrões.


Exemplos de padrões.

Plataformas

Antes de construir uma linha, o algoritmo examina a linha abaixo dela. Se a linha inferior não puder fornecer suporte para todos os quadrados acima dela, será necessária uma plataforma temporária. Quando a plataforma é removida, uma nova linha cai e, devido à maneira como a gravidade é implementada no Tetris original, alguns quadrados permanecem pairando no ar.

A ilustração abaixo mostra 10 padrões de plataforma. A construção da plataforma começa baixando o tetramino T em cima de um dos quadrados da última linha gerada. Os tetraminos restantes dependem desse primeiro T. Ou seja, se a linha gerada anterior contiver pelo menos 1 quadrado, como o quadrado vermelho na imagem abaixo, podemos criar uma plataforma plana acima dela para gerar a próxima linha.


No meio da construção da plataforma, a linha inferior é concluída e excluída, deixando três linhas acima dela. O último tetramino J ou L, que excluirá essas linhas, não será inserido até que os padrões de criação gerem a próxima linha de sprite na parte superior da plataforma. Esta última figura impede a criação de quadrados na primeira e na última duas linhas. Mas, como mencionado acima, devido à geometria dos tetraminos J, T e L usados ​​nesse processo, os padrões para a criação de quadrados são limitados a 17 colunas internas.

Além disso, das 19 maneiras possíveis de construir plataformas sobre o Tetramino T, apenas 10 são mostradas acima.

Matrizes embaladas

Como mencionado acima, um subconjunto dos 6 padrões de criação de quadrados envolve a limpeza de apenas duas linhas. Todos os outros padrões requerem 6 linhas. Para entender por que esse é o caso, considere o padrão abaixo.


Esses tetraminos são intercambiáveis ​​com os tetraminos J e L, e cada um deles adiciona 3 quadrados adjacentes à linha comum. As linhas a serem preenchidas são representadas pela matriz mostrada abaixo.


Agora tudo está empacotando espaço vazio com tetramino. Começando à esquerda, a única opção é usar a sequência tetramino I.


A única maneira de preencher o espaço restante é usar J e O ou I e L. Ambas as opções são mostradas abaixo.



Infelizmente, o tetramino O e L não são suportados nas matrizes mostradas acima. Esse padrão de 6 quadrados requer uma matriz maior.

Um problema semelhante surge em dois padrões de criação de um quadrado. Considere a matriz abaixo:


A única maneira de preencher a linha inferior à direita é encadear a sequência Z.


Da mesma forma, a única maneira de obter 3 quadrados vazios no canto inferior esquerdo é tetramino S.

Na linha do meio, existe um quadrado vazio entre S e Z e a única maneira de preenchê-lo é usar o tetramino J, T ou L, como mostrado nas figuras abaixo.



Inserir qualquer uma dessas formas divide o espaço em branco. A área vazia à esquerda contém 5, 6 e 7 espaços vazios, respectivamente. Como nenhum desses valores é divisível por 4, é impossível continuar. Uma matriz maior é necessária para esse padrão quadrado único.

O mesmo se aplica a outro padrão para criar um quadrado, mostrado na matriz abaixo.


Depois de usar o tetramino S e Z para preencher a maior parte da linha inferior, há um espaço vazio entre eles na linha do meio.


Como mostrado nas imagens abaixo, a inserção do furo divide o espaço vazio e a área vazia à esquerda contém 9, 10 ou 11 quadrados, respectivamente; nenhum dos números é divisível por 4.



Mas as matrizes de empacotamento não são a única maneira de gerar um padrão de quadrados. Por exemplo, dê uma olhada no criador de 4 quadrados abaixo.


A seguir, é apresentada uma tentativa de renderizar o padrão como um conjunto de tetraminos empacotados.


O último L é ignorado, porque o espaço para ele é formado somente após a conclusão e remoção da terceira linha.

Mas, após uma pesquisa minuciosa, descobriu-se que essa técnica não fornece os padrões de um quadrado acima mencionados com a capacidade de trabalhar com apenas três linhas. Além disso, ele não permite implementar novos padrões de 6 quadrados em duas linhas. Não há necessidade de procurar os padrões restantes fora das matrizes compactadas, porque eles já usam a menor quantidade possível de tetramino. E nos limitando a matrizes compactadas, encontraremos todos os padrões necessários muito mais rapidamente.

Pesquisa de padrões

Para simplificar a saída de dados, o Tetris Printer Algorithm limita-se a criar o tetramino no ponto central superior do campo de jogo, girando-o, movendo-se horizontalmente e abaixando-o. Ele nunca precisa mover a figura horizontalmente depois de passar alguma distância. Essa restrição reduz bastante o espaço de busca, pois não permite a formação de lacunas nas figuras adicionadas à matriz. Como exemplo, vejamos a seguinte matriz de 3 quadrados.


Se jogarmos J no centro da matriz, como mostrado acima, obteremos um espaço de 2 quadrados vazios, que não podem ser preenchidos com figuras subsequentes. Portanto, a pesquisa não seguirá esse caminho.


Como as lacunas cobertas não são permitidas, cada coluna na matriz pode ser considerada como uma pilha de quadrados preenchidos e a altura dessas pilhas descreve completamente o conteúdo de toda a matriz. Independentemente do número de linhas, uma matriz inteira unidimensional com 21 elementos será suficiente para descrever uma matriz bidimensional.

Quando uma figura cai na matriz, as alturas das pilhas das colunas correspondentes aumentam. Para acelerar esse processo, todos os tetraminos são analisados ​​previamente. Existem 19 turnos tetraminos, e a pesquisa considera cada um deles como uma figura única.


O Tetramino J no canto superior esquerdo da imagem ocupa 3 colunas. Ao abaixar na matriz, as alturas de 3 pilhas adjacentes aumentam em 1, 1 e 2 quadrados, respectivamente. Porém, antes que a figura possa ser baixada, o perfil inferior da figura deve corresponder ao perfil superior das respectivas pilhas. Se este J estivesse no chão do campo de jogo, em cada uma dessas colunas deveria haver intervalos de 1, 1 e 0 quadrados vazios. Como as folgas são proibidas, as alturas relativas de 3 pilhas terão que corresponder totalmente ao padrão.

Outra consequência da falta de lacunas foi que, quando os números caem na matriz, as linhas são preenchidas de baixo para cima. Não é possível preencher uma linha no meio de uma matriz antes ou simultaneamente não concluir todas as linhas abaixo dela. No processo de preenchimento da matriz, seu limite inferior realmente se move para cima. Consequentemente, uma pilha de colunas da matriz pode fornecer suporte apenas se sua altura menos o número de linhas concluídas for maior que 0. Quando uma forma é adicionada à matriz, pelo menos uma das colunas correspondentes deve fornecer suporte.

A pesquisa armazena uma segunda matriz unidimensional que contém o número de quadrados preenchidos em cada linha. O J acima contém nas linhas correspondentes 3 e 1 um quadrado. Quando você o insere na matriz, esses valores são adicionados aos elementos correspondentes da matriz. O número de linhas concluídas é o número de elementos com um valor 21.

Conforme indicado na seção anterior, se a figura adicionada dividir a matriz, os tamanhos das áreas resultantes deverão ser divididos por 4. Por exemplo, na imagem abaixo, a adição de I cria 2 áreas, cada uma contendo 46 quadrados vazios. Como 46 não é divisível por 4, não há mais como preencher o restante da matriz.


A separação aparece quando a altura da pilha é igual à altura da matriz. Após inserir a figura incrementando as alturas das respectivas pilhas, as dimensões de todas as áreas divididas de espaço vazio podem ser determinadas digitalizando a matriz de alturas e somando o espaço restante em cada pilha. Este número é verificado e redefinido quando uma divisão é detectada.

A pesquisa usada para gerar todos os padrões usa construção incremental aleatória, um algoritmo de retorno que verifica sistematicamente todas as combinações em ordem aleatória. A construção incremental de uma solução inserindo formas aleatoriamente faz com que ela cresça como um cristal. A aleatoriedade fornece uma irregularidade contendo faces quebradas que servem como base para as formas adicionadas subsequentes. A maior parte da matriz é empacotada aleatoriamente muito rapidamente e, quando o espaço vazio se torna escasso, o retrocesso entra em ação.

Antes de realizar a pesquisa, são executadas permutações aleatórias de 371 maneiras de adicionar uma figura à matriz. O pseudo-código da função de pesquisa é mostrado abaixo.

private Result search(Matrix matrix, int remaining) { if (remaining == 0) { return SOLUTION } attempts := attempts + 1 if (attempts >= MAX_ATTEMPTS) { return TIMEOUT } if (     S  Z) {        S  Z if (  ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION }       if (result == TIMEOUT) { return TIMEOUT } } }          for(   ,    ) {      if (   ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION }       if (result == TIMEOUT) { return TIMEOUT } } } return NO_SOLUTION } 

A matriz original transmitida para a função de pesquisa está vazia, exceto a linha inferior que contém blocos de 3 quadrados adjacentes. É transmitido junto com o número de figuras restantes que precisam ser adicionadas. Se o remaining for 0, a matriz contém a solução e a função retorna. Cada chamada recursiva aumenta o número global de attempts . Se exceder MAX_ATTEMPTS , que tem um valor de 1000, a pesquisa será iniciada novamente.

A terceira if tenta adicionar o tetramino S ou Z à parte inferior da matriz, se o espaço permitir. O significado disso é evitar situações como a mostrada abaixo, quando o algoritmo gasta tempo preenchendo parte da matriz, não podendo preencher o restante devido à falta de suporte.


Graças à if ele rapidamente forma uma plataforma na qual construir:


Para tentar adicionar uma figura à matriz, as verificações acima são necessárias. O algoritmo verifica se a figura terá suporte, dadas as linhas concluídas. Ele também verifica se divide por 4 o tamanho de cada espaço vazio individual criado pela inserção da forma.

Conversão de imagem

O algoritmo da impressora Tetris converte cada linha do bitmap em uma série de passes. Movendo-se da esquerda para a direita, cada passagem de maneira "gananciosa" insere o tetramino J, T e L no local onde estão colocados. Por exemplo, a imagem abaixo mostra uma linha de 16 pixels de um bitmap.


A imagem abaixo mostra as 5 passagens necessárias para cobrir esses 16 pixels.






A sequência de formas que o algoritmo está tentando inserir é determinada pelas cores dos pixels. Para que as formas não se sobreponham, é usada uma matriz unidimensional de valores booleanos. Para inserir uma figura, 3 elementos zero devem estar presentes na matriz. Após a inserção bem-sucedida da figura 3, os elementos correspondentes da matriz assumem o valor 1.

Para rastrear pixels completos entre várias passagens, é usada uma segunda matriz unidimensional de valores booleanos. Quando cada item é 1, a linha está completa.

No final de cada passagem, o conversor de imagens pesquisa todos os padrões na tabela para criar um ou mais quadrados. Na saída, ele passa o padrão correspondente com o tetramino J, T e L. inserido na parte inferior.Por exemplo, a primeira passagem mostrada acima é exibida como o seguinte padrão para criar 5 quadrados:

Pesquisa em tempo real

O conversor de imagem descrito na seção anterior é extremamente rápido, pois utiliza uma tabela constante contendo todos os padrões para a criação de quadrados e não os pesquisa em tempo real. No entanto, a pesquisa em tempo real pode usar padrões que não estão na tabela e, portanto, reduzir bastante a quantidade de tetramino necessária para gerar a imagem. Ele usa os quadrados criados em passagens anteriores, usando-os como suportes adicionais. Por exemplo, como mencionado acima, o padrão a seguir para criar um quadrado requer 7 linhas completas.


Mas um quadrado vermelho criado na passagem anterior no canto inferior esquerdo da imagem abaixo fornece suporte adicional, reduzindo o número de linhas preenchidas para 3.


Além disso, uma pesquisa em tempo real pode cobrir 3 pixels adjacentes da mesma cor, girando o tetramino J, T ou L.


De fato, ele pode combinar tetramino invertido e invertido, cobrindo um grande número de pixels em uma passagem. Por exemplo, as 5 passagens acima necessárias para cobrir 16 pixels podem ser reduzidas à passagem única mostrada abaixo.


Para obter esse padrão, o conversor de imagem começa empacotando avidamente os tetraminos J, T e L.


Em seguida, ele tenta ansiosamente adicionar as versões não-giradas e, nesse caso, ele consegue adicionar outro J.


Em princípio, uma tabela de pesquisa pré-calculada também pode ser usada nesse processo, mas o tamanho de uma tabela torna-a inaplicável na prática.

Neste exemplo, 8 quadrados em uma linha acima da linha a ser criada são adicionados à linha inferior da matriz vazia. Para n quadrados em um campo de jogo de 21 quadrados, a altura da matriz h é o menor número inteiro positivo, de modo que 21h - n é divisível por 4. Nesse caso, é necessária uma matriz de altura 4.


A pesquisa em tempo real funciona exatamente da mesma maneira que o algoritmo de pesquisa descrito acima, mas possui pequenas melhorias. Como antes, a pilha da coluna da matriz fornece suporte apenas se a altura da coluna menos o número de linhas concluídas for maior que zero. Quando a diferença é zero, a pilha da coluna não deve fornecer suporte. No entanto, nesta versão, se for igual a zero, verifica os quadrados na linha criada gerada pelos passes anteriores. Ou seja, quaisquer quadrados na linha abaixo da linha inferior da matriz fornecem suporte para colunas vazias.

Além disso, como a pesquisa é realizada em tempo real, será impraticável torná-la exaustiva. Se ele não encontrou uma solução após um determinado número de tentativas, ele adiciona mais 4 linhas na parte superior da matriz e tenta novamente. Depois disso, se ele ainda não conseguiu encontrar uma solução após um determinado número de tentativas, na passagem atual ele volta ao método com tabelas de pesquisa pré-calculadas e conversão de imagens descritas na seção anterior do artigo.

Impressão

Para imprimir, você deve seguir as instruções exibidas pelo conversor de imagens no campo de reprodução Tetris. A impressora cria um tetramino específico no ponto central superior do campo de jogo em uma orientação padrão. Em seguida, a impressora gira, move horizontalmente e abaixa. Este processo é mostrado no vídeo:

Código fonte

O código fonte do projeto Java 7 está disponível aqui .

Os algoritmos de pesquisa para tabelas pré-preparadas e em tempo real estão nos pacotes search.precomputed e search.realtime . Eles usam algumas classes comuns localizadas no pacote de search . Os resultados de uma pesquisa pré-calculada são armazenados no pacote de patterns como uma sequência de arquivos de texto. Os arquivos de texto armazenam matrizes compactadas como caracteres ASCII, começando com A Por exemplo, as 3 primeiras matrizes em emitters1.txt (o conjunto de padrões para criar um quadrado) são assim:


Como indicado repetidamente no artigo, três símbolos A adjacentes nas matrizes acima podem ser substituídos pelos tetramino J, T ou L. Os símbolos B , C , D e assim por diante representam a sequência de tetramino que você precisa criar.

A classe imageconverter.ImageConverter contém o método main , que recebe um único argumento de linha de comando: o nome do arquivo de imagem sprite. Uma imagem não pode ter mais que 17 × 32 pixels e não pode conter mais de 3 cores opacas. Todos os outros pixels devem ser transparentes.

Curiosamente, em videogames antigos, os desenvolvedores costumavam usar o plano de fundo para obter cores extras. Por exemplo, os alunos e a boca da bolha do Bubble bobble, os alunos do Donkey Kong do Donkey Kong e a sobrancelha com a toupeira da Srta. Pac-Man é realmente transparente. O preto é obtido de um fundo sólido.


O pano de fundo do campo de jogo do Tetris pode ser usado de maneira semelhante.

ImageConverter saída do ImageConverter parece com este trecho:


Os 3 valores hexadecimais da primeira linha são 3 cores opacas extraídas do arquivo de imagem do sprite. Eles correspondem às cores do tetramino J, T e L. As cores do outro tetramino não afetam a imagem. Os blocos restantes são padrões empacotados executados no campo de jogo (para caracteres após Z e até a a consulte a tabela de caracteres ASCII ). Os blocos amarelos destacados compõem a plataforma. O primeiro bloco adiciona a plataforma, o segundo a remove.

A classe printer.Printer recebe um arquivo de texto nesse formato e gera um arquivo de imagem tocando no Tetris.

O algoritmo da impressora usado para gerar um vídeo semelhante à versão NES do Tetris define cada tipo de tetramino em cada bloco de um arquivo de texto. Em seguida, ele se move na ordem oposta do ponto inicial e da orientação inicial até o ângulo de rotação e as coordenadas de abaixamento da figura indicada no arquivo. Nota: devido à velocidade extremamente alta dos números decrescentes, é impossível ir além do nível 30 na versão real do NES do Tetris. Supõe-se que a impressora transmita todos os seus comandos para o campo de jogo com rapidez suficiente. para compensar isso.

Para regenerar arquivos de padrão, use search.precomputed.PatternSearcher . Pode ser personalizado alterando as constantes no início do arquivo de código-fonte.

 public static final int MATRIX_WIDTH = 21; public static final int MATRIX_HEIGHT = 4; public static final int EMITTED_SQUARES = 4; public static final int RANDOM_SETS = 100000; public static final int MAX_ATTEMPTS = 1000; 

RANDOM_SETS é o número de permutações aleatórias de 371 maneiras de adicionar uma figura à matriz. Quando definido como 100000 , leva alguns segundos para inicializar as permutações na inicialização. Além disso, seu armazenamento requer mais de um gigabyte de memória.

MAX_ATTEMPTS controla o tempo de execução de uma pesquisa. Um valor relativamente pequeno de 1000 permite que a pesquisa descarte rapidamente começos aleatórios que não conseguem se mostrar bem. No entanto, para provar que, para um tamanho de matriz específico e o número de quadrados criados, não há solução, é necessário explorar completamente todo o espaço de pesquisa. Para fazer isso, você pode definir MAX_ATTEMPTS como Integer.MAX_VALUE .

Constantes semelhantes são encontradas em search.realtime.RealtimeSearcher , que é usado pelo conversor de imagem. Como mencionado acima, um grande valor RANDOM_SETS requer um aumento na memória máxima e leva a um início mais longo. MAX_RETRIES controla o número de tentativas, após as quais a pesquisa em tempo real é MAX_RETRIES e retorna à pesquisa com uma tabela pré-calculada.

Lembre-se de que ambos os algoritmos de pesquisa usam 100% da CPU, criando muitos threads paralelos com tamanho igual ao número de processadores disponíveis.