Previsões vs explicações: ou por que mais “semi-compras” são necessárias no campo da ciência de dados

Phoebe Wong, cientista e diretora financeira da Equal Citizens, falou sobre o conflito cultural na ciência cognitiva. Elena Kuzmina traduziu o artigo para o russo.

Alguns anos atrás, assisti a uma discussão sobre processamento de linguagem natural. O “pai da linguística moderna” Noam Chomsky e o novo porta-voz da guarda, Peter Norvig , diretor de pesquisa do Google, falaram. Chomsky ponderou em que direção a esfera do processamento da linguagem natural está se movendo e disse :

Suponha que alguém esteja prestes a liquidar um departamento de física e queira fazê-lo de acordo com as regras. De acordo com as regras, é necessário gravar um número infinito de vídeos sobre o que está acontecendo no mundo, alimentar esses gigabytes de dados para o computador maior e mais rápido e realizar análises estatísticas complexas - bem, você entende: Bayesiano "para frente e para trás" * - e você obterá uma certa previsão sobre o que está prestes a acontecer fora da sua janela. De fato, você obterá uma previsão melhor do que a fornecida pela Faculdade de Física. Bem, se o sucesso é determinado pela proximidade com a massa de dados brutos caóticos, é melhor fazê-lo do que os físicos: sem experimentos de pensamento em superfícies ideais e assim por diante. Mas você não terá o tipo de entendimento que a ciência sempre buscou. O que você recebe é apenas uma idéia aproximada do que está acontecendo na realidade.

* Da probabilidade de Bayes - uma interpretação do conceito de probabilidade, na qual, em vez da frequência ou tendência a algum fenômeno, a probabilidade é interpretada como uma expectativa razoável, representando uma avaliação quantitativa de uma crença pessoal ou estado de conhecimento. Pesquisadores de inteligência artificial usam estatísticas bayesianas no aprendizado de máquina para ajudar os computadores a reconhecer padrões e tomar decisões com base neles.

Chomsky enfatizou repetidamente essa idéia: o sucesso de hoje no processamento de linguagem natural, ou seja, a precisão das previsões, não é uma ciência. Segundo ele, jogar um pedaço enorme de texto em uma “máquina complexa” é simplesmente aproximar dados brutos ou coletar insetos, não levará a um entendimento real da linguagem.

Segundo Chomsky, o principal objetivo da ciência é descobrir princípios explicativos de como o sistema realmente funciona, e a abordagem correta para atingir esse objetivo é permitir que a teoria direcione dados. É necessário estudar a natureza básica do sistema abstraindo de “inclusões irrelevantes” com a ajuda de experimentos cuidadosamente projetados, ou seja, da mesma maneira que foi aceito na ciência desde o tempo de Galileu.

Nas suas palavras:

É improvável que uma simples tentativa de lidar com dados caóticos brutos o leve a qualquer lugar, assim como o Galileo não o levaria a lugar algum.

Posteriormente, Norwig respondeu às alegações de Chomsky em um longo ensaio . Norvig observa que em quase todas as áreas da aplicação do processamento de idiomas: mecanismos de busca, reconhecimento de fala, tradução automática e perguntas respondidas, modelos probabilísticos treinados prevalecem porque funcionam muito melhor do que ferramentas antigas baseadas em regras teóricas ou lógicas. Ele diz que o critério de sucesso de Chomsky na ciência - a ênfase na pergunta "por que" e a subavaliação da importância de "como" - está errada.

Confirmando sua posição, ele cita Richard Feynman: "A física pode se desenvolver sem evidências, mas não podemos nos desenvolver sem fatos". Norwig lembra que os modelos probabilísticos geram vários trilhões de dólares por ano, enquanto os descendentes da teoria de Chomsky ganham muito menos que um bilhão, citando os livros de Chomsky vendidos na Amazon.

Norwig sugere que o desprezo de Chomsky por “retroceder bayesiano” se deve à divisão entre as duas culturas na modelagem estatística descrita por Leo Breiman:

1. Uma cultura de modelagem de dados que assume que a natureza é uma caixa preta na qual as variáveis ​​são conectadas estocamente. O trabalho dos especialistas em modelagem é determinar o modelo que melhor se ajusta às associações subjacentes a ele.
2. A cultura da modelagem algorítmica implica que as associações em uma caixa preta são muito complexas para serem descritas usando um modelo simples. O trabalho dos desenvolvedores de modelos é selecionar o algoritmo que melhor avalia o resultado usando variáveis ​​de entrada, sem esperar que as verdadeiras associações básicas de variáveis ​​dentro da caixa preta possam ser entendidas.

Norwig sugere que Chomsky não é tão polêmico com modelos probabilísticos como tais, mas não aceita modelos algorítmicos com "parâmetros de quadrilhão": eles não são fáceis de interpretar e, portanto, são inúteis para resolver as questões do "porquê".
Norwig e Breiman pertencem a outro campo - eles acreditam que sistemas como idiomas são muito complexos, aleatórios e arbitrários para serem representados por um pequeno conjunto de parâmetros. E abstrair das dificuldades é semelhante a fazer uma ferramenta mística afinada para uma determinada área permanente que na verdade não existe, e, portanto, a questão de o que é a linguagem e como ela funciona é ignorada.

Norwig reafirma sua tese em outro artigo , onde argumenta que devemos parar de agir como se nosso objetivo fosse criar teorias extremamente elegantes. Em vez disso, você precisa aceitar a complexidade e usar nossa melhor aliada - eficiência de dados irracional. Ele ressalta que, no reconhecimento de fala, tradução automática e quase todos os aplicativos de aprendizado de máquina para dados da Web, modelos simples como modelos n-gram ou classificadores lineares baseados em milhões de funções específicas funcionam melhor que modelos complexos. que estão tentando descobrir as regras gerais.

O que mais me atrai nesta discussão não é o que Chomsky e Norvig discordam, mas o que eles estão unidos. Eles concordam que a análise de grandes quantidades de dados usando métodos estatísticos de aprendizado sem entender as variáveis ​​fornece melhores previsões do que uma abordagem teórica que tenta modelar como as variáveis ​​se relacionam.

E não sou o único que fica intrigado com isso: muitas pessoas com formação matemática com quem conversei também acham isso contraditório. A abordagem que não é mais adequada para modelar relacionamentos estruturais básicos também deve ter o maior poder preditivo? Ou como podemos prever com precisão algo sem saber como tudo funciona?

Previsões Contra Causação

Mesmo em campos acadêmicos, como economia e outras ciências sociais, os conceitos de poder preditivo e explicativo são frequentemente combinados entre si.

Modelos que demonstram alta capacidade de explicação são frequentemente considerados altamente preditivos. Mas a abordagem para construir o melhor modelo preditivo é completamente diferente da abordagem para criar o melhor modelo explicativo, e as decisões de modelagem geralmente levam a compromissos entre os dois objetivos. As diferenças metodológicas são ilustradas em Introdução à aprendizagem estatística (ISL).

Modelagem preditiva

O princípio fundamental dos modelos preditivos é relativamente simples: avalie Y usando um conjunto de dados de entrada prontamente disponíveis X. Se o erro X for em média zero, Y pode ser previsto usando:

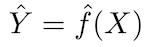
onde ƒ é a informação sistemática sobre Y fornecida por X, que leva a Ŷ (previsão de Y) para um dado X. A forma funcional exata geralmente não é significativa se ela predizer Y e ƒ é considerada uma “caixa preta”.

A precisão desse tipo de modelo pode ser decomposta em duas partes: um erro redutível e um erro fatal:

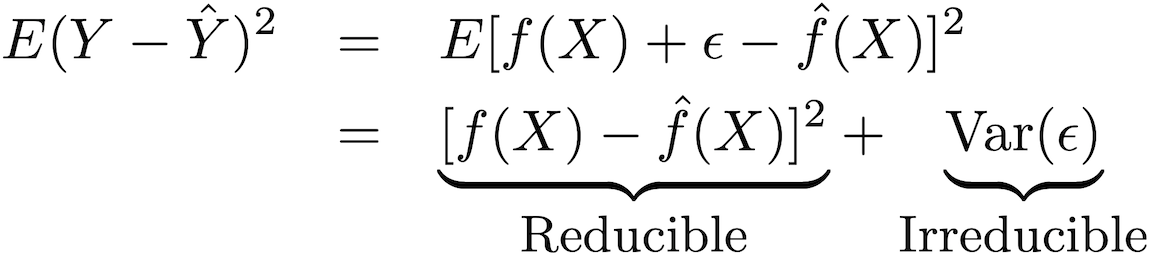
Para aumentar a precisão da previsão do modelo, é necessário minimizar o erro redutível, utilizando os métodos mais adequados de treinamento estatístico para estimativa, a fim de avaliar

Modelagem de saída

ƒ não pode ser considerado como uma “caixa preta” se o objetivo é entender a relação entre X e Y (como Y muda em função de X). Porque não podemos determinar o efeito de X em Y sem conhecer a forma funcional ƒ.

Quase sempre ao modelar conclusões, métodos paramétricos são usados ​​para estimar ƒ. O critério paramétrico refere-se a como essa abordagem simplifica a estimativa de ƒ assumindo a forma paramétrica ƒ e avaliando ƒ através dos parâmetros propostos. Existem duas etapas principais nessa abordagem:

1. Faça uma suposição sobre a forma funcional ƒ. A suposição mais comum é que ƒ é linear em X:



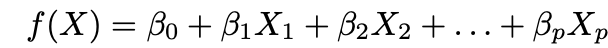
2. Use os dados para ajustar o modelo, ou seja, encontre os valores dos parâmetros β₀, β₁, ..., βp de modo que:


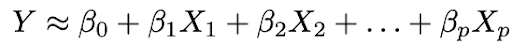
A abordagem de ajuste de modelo mais comum é o método dos mínimos quadrados (OLS).

A troca entre flexibilidade e interpretabilidade

Você já deve estar se perguntando: como sabemos que ƒ é linear? De fato, não saberemos, pois a verdadeira forma ƒ é desconhecida. E se o modelo selecionado estiver muito longe do real ƒ, nossas estimativas serão tendenciosas. Então, por que queremos fazer essa suposição em primeiro lugar? Porque existe um compromisso inerente entre flexibilidade e interpretabilidade do modelo.

Flexibilidade refere-se ao intervalo de formas que um modelo pode criar para ajustar-se às diversas formas funcionais possíveis. Portanto, quanto mais flexível o modelo, melhor o ajuste que ele pode criar, o que aumenta a precisão da previsão. Mas um modelo mais flexível é mais complexo e requer mais parâmetros para se ajustar, e as estimativas gerais geralmente se tornam muito complexas para que as associações de quaisquer preditores individuais e fatores prognósticos sejam interpretadas.

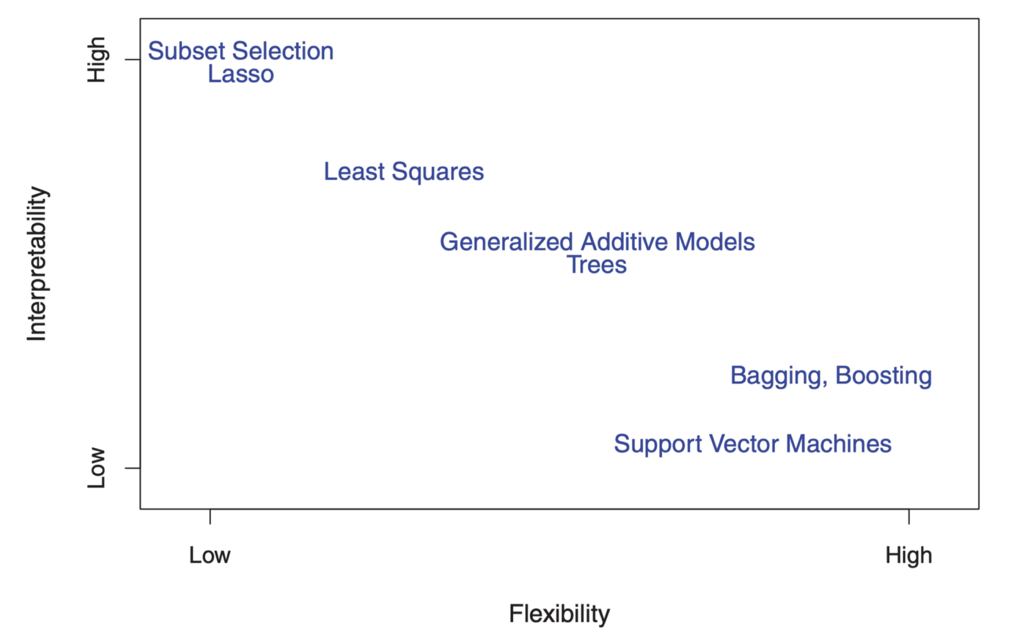
Por outro lado, os parâmetros no modelo linear são relativamente simples e interpretáveis, mesmo que não executem uma previsão precisa muito bem. Aqui está um ótimo diagrama no ISL que ilustra esse compromisso em vários modelos de treinamento estatístico:
" "

Como você pode ver, modelos de aprendizado de máquina mais flexíveis e com melhor precisão de previsão, como o método do vetor de suporte e os métodos de aprimoramento, têm ao mesmo tempo baixa interpretabilidade. A modelagem de inferência também recusa a precisão da previsão do modelo interpretado, assumindo com segurança a forma funcional f.

Identificação Causal e Raciocínio Contrafactual

Mas espere um momento! Mesmo se você usar um modelo bem interpretado com bom ajuste, ainda não poderá usar essas estatísticas como uma evidência separada de causalidade. Isso se deve ao velho e cansado clichê "correlação não é causalidade".

Aqui está um bom exemplo : suponha que você tenha dados sobre o comprimento de cem mastros de bandeira, o comprimento de suas sombras e a posição do sol. Você sabe que o comprimento da sombra é determinado pelo comprimento do pólo e pela posição do Sol, mas mesmo se você definir o comprimento do pólo como uma variável dependente e o comprimento da sombra como uma variável independente, seu modelo ainda ajustará coeficientes estatisticamente significativos e assim por diante.

É por isso que as relações causais não podem ser feitas apenas por modelos estatísticos e requerem conhecimento básico - a alegada causalidade deve ser justificada por algum entendimento teórico preliminar da relação. Portanto, a análise de dados e a modelagem estatística das relações de causa e efeito geralmente são baseadas em modelos teóricos.

E mesmo se você tiver uma boa justificativa teórica para dizer que X causa Y, identificar um efeito causal ainda é muitas vezes muito difícil. Isso ocorre porque avaliar uma relação causal envolve identificar o que aconteceria em um mundo contra-ativo no qual X não ocorreu, o que, por definição, não é observável.

Aqui está outro bom exemplo : suponha que você queira determinar os efeitos na saúde da vitamina C. Você tem dados sobre se alguém está tomando vitaminas (X = 1 se estiver tomando; 0 - não está tomando) e alguns resultados binários de saúde (Y = 1 se eles estão saudáveis; 0 - não estão saudáveis) é assim:

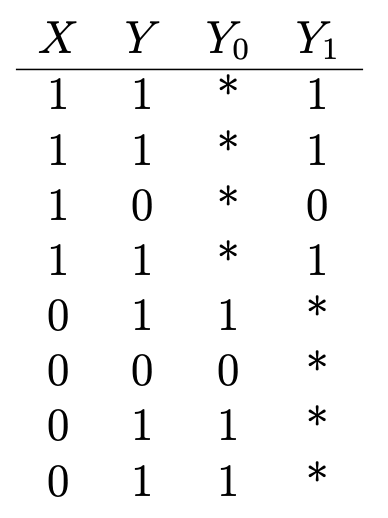
Y₁ é o resultado da saúde daqueles que tomam vitamina C e Y₀ é o resultado da saúde daqueles que não tomam. Para determinar o efeito da vitamina C na saúde, avaliamos o efeito médio do tratamento:

$$$= E (A) - E (A)$

Mas, para fazer isso, é importante saber quais seriam as consequências para a saúde daqueles que tomam vitamina C se não tomarem vitamina C e vice-versa (ou E (Y₀ | X = 1) e E (Y₁ | X = 0)), que são indicados por asteriscos na tabela e representam resultados contrafatuais não observados. O efeito médio do tratamento não pode ser avaliado sequencialmente sem essa entrada.

Agora imagine que pessoas já saudáveis, em regra, tentam tomar vitamina C, mas pessoas que já não são saudáveis ​​não. Nesse cenário, as avaliações mostrariam um forte efeito curativo, mesmo que a vitamina C não tivesse realmente afetado a saúde. Aqui, o estado anterior de saúde é chamado de fator misto, que afeta a ingestão e a saúde de vitamina C (X e Y), o que leva a estimativas distorcidas. A maneira mais segura de obter uma pontuação θ consistente é randomizar o tratamento através do experimento, para que X não dependa de Y.

Quando o tratamento é prescrito aleatoriamente, o resultado do grupo que não recebe o medicamento, em média, torna-se um indicador objetivo dos resultados contrafatuais do grupo que recebe o tratamento e garante que não haja fator de distorção. O teste A / B é guiado por esse entendimento.

Mas experimentos aleatórios nem sempre são possíveis (ou éticos, se queremos estudar os efeitos na saúde de fumar ou comer muitos biscoitos de chocolate) e, nesses casos, os efeitos causais devem ser estimados a partir de observações com tratamento frequentemente não randomizado.

Existem muitos métodos estatísticos que identificam efeitos causais em condições não experimentais. Eles fazem isso construindo resultados contrafactuais ou modelando prescrições aleatórias de tratamento em dados observacionais.

É fácil imaginar que os resultados desses tipos de análise geralmente não são muito confiáveis ​​ou reprodutíveis. E ainda mais importante: esses níveis de obstáculos metodológicos não visam melhorar a precisão da previsão do modelo, mas apresentar evidências de causalidade por meio de uma combinação de conclusões lógicas e estatísticas.

É muito mais fácil medir o sucesso de um modelo prognóstico do que causal. Embora existam indicadores de desempenho padrão para modelos prognósticos, é muito mais difícil avaliar o sucesso relativo de modelos causais. Mas se for difícil rastrear causa e efeito, isso não significa que devemos parar de tentar.
O ponto principal aqui é que modelos prognósticos e causais servem a propósitos completamente diferentes e requerem dados completamente diferentes e processos de modelagem estatística, e geralmente precisamos fazer os dois.

Um exemplo da indústria cinematográfica ilustra: os estúdios usam modelos de previsão para prever bilheteria, prever os resultados financeiros da distribuição de filmes, avaliar os riscos financeiros e a lucratividade de seu portfólio de filmes, etc. decisões de investimento, porque nos estágios iniciais do processo de produção do filme (geralmente anos antes da data de lançamento), quando as decisões de investimento são tomadas, a variação possível Os resultados são altos.

Portanto, a precisão dos modelos de previsão com base nos dados iniciais nos estágios iniciais é bastante reduzida. Modelos preditivos estão se aproximando da data de início da distribuição do filme, quando a maioria das decisões de produção já foi tomada e a previsão não é mais particularmente viável e relevante. Por outro lado, a modelagem das relações de causa e efeito permite que os estúdios descubram como várias características da produção podem influenciar a renda potencial nos estágios iniciais da produção do filme e, portanto, são cruciais para informar sobre suas estratégias de produção.

Maior atenção às previsões: Chomsky estava certo?

É fácil entender por que Chomsky está chateado: modelos prognósticos dominam a comunidade científica e a indústria. Uma análise textual das pré-impressões acadêmicas mostra que as áreas de crescimento mais rápido da pesquisa quantitativa estão prestando cada vez mais atenção às previsões. Por exemplo, o número de artigos no campo da inteligência artificial que mencionam "previsão" mais que dobrou, enquanto os artigos sobre conclusões caíram pela metade desde 2013.

Os currículos de ciência de dados ignoram amplamente as relações de causa e efeito. E a ciência de dados nos negócios se concentra principalmente em modelos preditivos. Competições de campo de prestígio, como o prêmio Kaggle e Netflix, são baseadas na melhoria dos indicadores preditivos de desempenho.

Por outro lado, ainda existem muitas áreas nas quais atenção insuficiente é dada à previsão empírica e elas podem se beneficiar das conquistas obtidas no campo de aprendizado de máquina e modelagem preditiva. Mas apresentar a situação atual como uma guerra cultural entre a "Equipe Chomsky" e a "Equipe Norvig" está incorreto: não há razão para que seja necessário escolher apenas uma opção, porque há muitas oportunidades de enriquecimento mútuo entre as duas culturas. Muito trabalho foi feito para tornar os modelos de aprendizado de máquina mais compreensíveis. Por exemplo, Susan Ati, de Stanford, usa métodos de aprendizado de máquina em uma metodologia de relacionamento causal.

Para terminar com uma nota positiva, lembre-se das obras de Jude Pearl . Pearl liderou um projeto de pesquisa em inteligência artificial na década de 1980, que permitiu que as máquinas raciocinassem probabilisticamente usando redes bayesianas. No entanto, desde então, ele se tornou o maior crítico de como a atenção da inteligência artificial exclusivamente às associações e correlações probabilísticas se tornou um obstáculo para as conquistas.

Compartilhando a opinião de Chomsky, Pearl argumenta que todas as realizações impressionantes do aprendizado profundo se resumem em ajustar a curva aos dados. , ( ), 30 . , — « ».

, - , , — , , .

, - , , . em um de seus artigos, ele afirma:

A maior parte do conhecimento humano é organizada em torno de relações causais, e não probabilísticas, e a gramática do cálculo de probabilidade não é suficiente para entender essas relações ... É por esse motivo que me considero apenas metade bayesiana.

Parece que a ciência de dados só vencerá se tivermos mais petiscos.