Olá Habr! Apresento a você a tradução do artigo
"Uma explicação intuitiva do Teste de Hipóteses e Valores-P", de Joos Korstanje.
Alguns anos atrás, fiz meu primeiro trabalho de estatística freelancer em uma empresa de entrega de frutas e vegetais. Vinte e quatro horas por dia, os produtos recebidos dos agricultores, antes de serem enviados aos supermercados, passavam pelo departamento de controle de qualidade. A escolha dos produtos foi realizada aleatoriamente pelos funcionários desse departamento.
No relatório anual, eles perceberam que a qualidade deste ano é inferior à qualidade do passado: a diferença era de cerca de meio ponto em uma escala de 1 a 10.
Então eles me convidaram. Eu tive que responder à pergunta:
Estes 0,5 pontos são uma diferença significativa?Se você não conhece as estatísticas, essa pergunta pode parecer estranha para você. Mas não se preocupe: o objetivo deste artigo é mostrar como você pode responder a essa pergunta usando o teste de hipóteses, também chamado de inferência estatística.
O jogo dos números: a contribuição de uma maçã
Imagine que você está verificando uma maçã como boa ou ruim, usando uma seleção aleatória de maçãs de uma caixa muito grande com maçãs. Na imagem abaixo, vemos o efeito real do tamanho da amostra nas medições: o efeito de uma maçã é muito significativo para amostras pequenas e se torna cada vez menos significativo, quanto maior o tamanho da amostra.
A contribuição de uma maçã depende do tamanho da amostra.Compreender o efeito do tamanho da amostra é a primeira base para entender o teste de hipóteses. Podemos começar a argumentar que 0,5 em 2 maçãs será como uma diferença de 1 maçã, muito pequena. Mas para 100 maçãs, 0,5 será uma diferença de 50 maçãs: uma diferença muito grande!
Para amostras pequenas, 0,5 pontos é uma pequena diferença, mas para amostras grandes 0,5, essa é uma grande diferença.Qual o tamanho da amostra: teste de hipóteses e significado como resposta
Existem várias maneiras de responder a essa pergunta, mas neste artigo vou mergulhar na inferência estatística ou no teste de hipóteses.
O teste de hipóteses é uma família de métodos estatísticos usados para entender como a amostragem de objetos observados pode ser usada para aceitar ou rejeitar uma hipótese predefinida. O teste de hipóteses é usado para resolver muitos problemas, principalmente em pesquisas científicas e como método chave no marketing on-line (teste A / B).
Os matemáticos desenvolveram um teste de hipóteses de tal maneira que existe um certo procedimento para encontrar a verdade.
O teste de hipóteses permite testar apenas hipóteses, mas não as desenvolver.Da caixa em que 100 maçãs (vamos chamar de população), coletamos uma amostra de 8 maçãs. Este ano, das 8 maçãs, 5 estavam apodrecidas (62%) e, na amostra do ano passado, das 8 maçãs, apenas 4 estavam apodrecidas (50%). Queremos usar um teste de hipótese para determinar se a porcentagem de maçãs podres neste ano é maior que no ano passado.
O teste de hipóteses é uma alternativa matemática para medir a população. Graças a esses cálculos, podemos generalizar as medidas de uma pequena amostra para uma grande população. Então, fazemos menos trabalho.
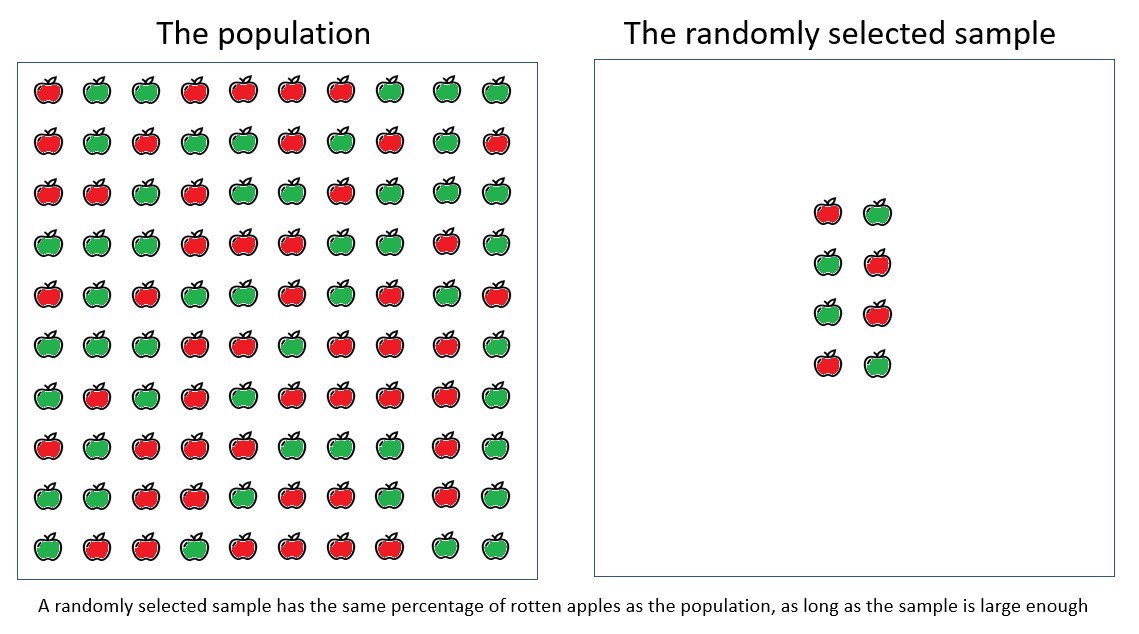
Uma amostra amostrada aleatoriamente tem a mesma porcentagem de maçãs podres que a população em geral, desde que a amostra seja grande o suficiente.
Os matemáticos criaram uma maneira de generalizar a conclusão com base na amostra para a população em geral.
Este método começa com a formulação de uma clara hipótese de pesquisa. Infelizmente, a matemática só funciona se já tivermos uma idéia do que queremos testar.
A principal hipótese para o nosso exemplo:
A porcentagem de maçãs podres na população em geral este ano é mais do que no passado.Teste de hipótese real
A matemática do teste de hipóteses forma um equilíbrio entre o resultado das medições da amostra e o número de observações. O resultado é um valor-p.Esses cálculos passam pelo uso de distribuições: para quase todas as situações imaginárias, foi derivada uma lei matemática que descreve o resultado esperado.
Para perguntas de sim / não, como a de nossas maçãs podres (podres / não podres), aplica-se a lei do lançamento de moedas. Este é o exemplo mais simples de uma lei matemática: 50% caudas, 50% águia.
Também pode ser muito simplesmente representado como uma distribuição matemática padrão que nos informa sobre a probabilidade de observações. Por exemplo, 7 águias caíram de 10 lançamentos de moedas. Isso é chamado de distribuição binomial e pode ser representado da seguinte maneira:
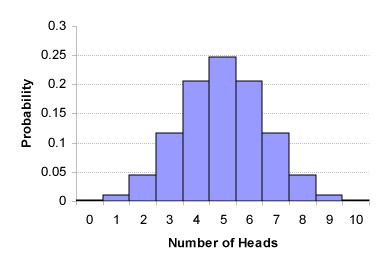distribuição binomial de 10 lançamentos de moedas.Neste artigo, estarei longe da matemática difícil, mas é importante saber que podemos usar fórmulas matemáticas para avaliar se a porcentagem observada está longe da porcentagem esperada.
No final deste artigo, apresentarei uma lista de fórmulas de teste de hipóteses comumente usadas para vários casos e, posteriormente, explicarei como usá-las. Mas primeiro, explicarei a interpretação do teste de hipóteses.
Resultado do teste de hipótese: valor-p
Por trás do teste de hipóteses, há um equilíbrio matemático entre os valores observados e o tamanho da amostra. No final dos cálculos, cada opção de teste de hipótese existente produzirá uma pontuação padronizada que permite comparar o resultado mesmo quando a matemática não é exatamente a mesma.
O valor P é uma maneira padrão de formular um resultado de teste de hipótese e usá-lo em outros testes.
O valor P é um número entre 0 e 1 que nos diz se a diferença está entre nossas observações das amostras e nossas hipóteses são muito diferentes. O valor de referência é 0,05.
A diferença é estatisticamente significativa se o valor de p for menor que 0,05.
E a diferença não é estatisticamente significativa se o valor de p for maior que 0,05.
Exemplo 1:
Fizemos 10 lançamentos de moedas.
Nossa hipótese: esperamos 5 caudas.
Nossas observações: temos 6 caudas.
O cálculo do valor-p rendeu 0,518, que é maior que 0,05.
Nossa conclusão: a diferença não é estatisticamente significante.
Nossa interpretação: o resultado é consistente com a hipótese.
Exemplo 2:
Fizemos 10 lançamentos de moedas
Nossa hipótese: esperamos 5 caudas.
Nosso resultado: conseguimos 10 caudas.
Nosso valor de p é 0,0, que é menor que 0,05.
Nossa conclusão: a diferença é estatisticamente significante
Nossa interpretação: o resultado não é consistente com a hipótese.
Exemplo 3:
Verificamos 10 maçãs.
Nossa hipótese: esperamos uma maçã podre.
O nosso resultado: conseguimos 1 maçã podre.
Nosso valor de p é 1,0, que é mais do que 0,05.
Nossa conclusão: a diferença não é estatisticamente significante
Nossa interpretação: o resultado é consistente com a hipótese.
Exemplo 4:
Verificamos 10 maçãs.
Nossa hipótese: esperamos uma maçã podre.
O nosso resultado: conseguimos 5 maçãs podres.
Nosso valor de p é 0,0114, que é menor que 0,05.
Nossa conclusão: a diferença é estatisticamente significante
Nossa interpretação: o resultado não é consistente com a hipótese.
Conclusão
Neste artigo, dei uma interpretação intuitiva da estrutura geral de erros estatísticos ou teste de hipóteses. Espero que agora você entenda melhor o teste de hipóteses e como ele pode ser útil para você.
Não mergulhei em provas matemáticas nem em detalhes específicos. A tabela abaixo fornece uma lista dos testes de hipóteses mais frequentes que recomendo para um estudo mais aprofundado.
Uma lista com hipóteses alternativas para alguns testes de hipóteses.
Espero que este artigo seja útil para você e desejo boa sorte em pesquisas adicionais sobre testes de hipóteses.