Todos os dias a web global é reabastecida com artigos sobre os algoritmos de aprendizado de máquina mais populares e usados para solucionar vários problemas. Além disso, a base desses artigos, ligeiramente alterada na forma de um lugar ou de outro, passa de um pesquisador de dados para outro. Além disso, todos esses trabalhos são unidos por um postulado geralmente aceito e incontestável: a aplicação de um ou outro algoritmo de aprendizado de máquina depende do tamanho e da natureza dos dados disponíveis e da tarefa em questão.
Além disso, pesquisadores de dados especialmente insistidos, compartilhando sua experiência, enfatizam:
“A escolha de um método de avaliação deve depender parcialmente dos seus dados e do que, na sua opinião, o modelo deve ser bom” (“Ciência de Dados: informações privilegiadas para iniciantes. Incluindo a linguagem R, de Cathy O'Neill, Rachel Shutt) .
Em outras palavras, um estatístico / pesquisador de dados deve ter não apenas experiência na área de assunto, mas também uma ampla gama de conhecimentos variados:
“Um pesquisador de dados é aquele que possui conhecimento nas seguintes áreas: matemática, estatística, engenharia da computação, aprendizado de máquina, visualização, meios de troca de dados ... ” (do mesmo livro). Somente o carregamento completo do conhecimento das áreas acima na cabeça pode ser abordado no aprendizado de máquina e encontrar soluções para os problemas indicados.
Quanto a mim, esse começo é bastante adequado para um livro comum de meio quilo e meio de ciência de dados, ou para um artigo de história de horror científico com fórmulas, símbolos e rabiscos de dois andares "inúteis" subsequentes que têm um impacto grave e deprimente para iniciantes no campo de aprendizado de máquina e apenas por acaso interessados nessa direção, leitores inexperientes, não sobrecarregados com o "conhecimento necessário". Além disso, o número 10 da rodada dos mesmos artigos sobre os 10 algoritmos de aprendizado de máquina mais populares (
por exemplo ) apenas reforça o efeito imposto.
No habr, eles também se distinguiram :
“A resposta à pergunta:“ Que tipo de algoritmo de aprendizado de máquina devo usar? ”Sempre soa assim:“ Dependendo das circunstâncias ”. A escolha do algoritmo depende do volume, qualidade e natureza dos dados. Depende de como você gerencia o resultado. Depende de como as instruções para o computador que o implementa foram criadas a partir do algoritmo e também de quanto tempo você tem. Mesmo os analistas de dados mais experientes não vão dizer qual algoritmo é melhor até que eles o testem. ”Sem dúvida, todo esse conhecimento, bem como perseverança e interesse, são necessários e úteis para alcançar bons resultados, não apenas no caminho para a compreensão do aprendizado de máquina, mas também em muitas outras áreas. Além disso, facilitarão o entendimento de que os algoritmos de aprendizado de máquina (a seguir denominados algoritmos) estão longe de uma dúzia; mas isso é apenas mais tarde, com estudo independente.
Meu objetivo é apresentar ao leitor os algoritmos mais utilizados de um ponto de vista prático e acessível. (O fato de eu não ser um programador e, além disso, não um matemático (santo-santo-santo!) Deve sublinhar o interesse na narrativa. O ensino de engenharia e a experiência no "assunto crescem" de 10 anos (apenas algum tipo de número mágico ) - como se costuma dizer, e todas as minhas coisas, todas as minhas malas com as quais fui direto para o aprendizado de máquina.Graças à experiência adquirida na indústria do petróleo, foram encontradas idéias para o uso de redes neurais artificiais e algoritmos de aprendizado de máquina (leia - eram necessárias conjuntos de dados.) Tudo o que restava era lidar com Scarlet - aprenda a distorcer os dados para enviá-los corretamente à entrada do "programa" e qual, de fato, o algoritmo a ser escolhido. E então em um círculo vicioso. Percebo que meu caminho era espinhoso e divertido - "balas assobiavam no alto" (de m / f "As aventuras de Funtik"), - mas ainda assim eu consegui fazer anotações e, se o interesse for indicado, no futuro publicarei outras mensagens.)
Então, proponho abordar a "usinagem", por outro lado: por que não alimentar seu conjunto de dados existente (nos exemplos você carregará conjuntos de dados que podem ser facilmente treinados) para vários algoritmos de uma só vez e, de acordo com os resultados, decida qual deles deve prestar mais atenção estudo cuidadoso subsequente e seleção de parâmetros ideais que melhoram o resultado. Além disso, o principal valor do método discutido acima é que seus resultados responderão à pergunta sobre o valor de seu conjunto de dados:
"comece resolvendo o problema e verifique se você tem algo para otimizar" (também de alguns então as estatísticas insistentes diziam "respeito" a ele, um bom conselho!).
Como é feito?
Sabe-se que a maior parte dos problemas resolvidos com a ajuda de algoritmos está relacionada aos problemas de classificação (classificação) e análise de regressão (análise preditiva). Por
classificação entende-se uma diferenciação constante de unidades de observação (instâncias) de um conjunto de dados para uma determinada categoria (classe) com base nos resultados do treinamento.
A análise de regressão é um conjunto de métodos e processos estatísticos para avaliar a relação entre variáveis [
Statistics: Textbook / Ed. prof. M.R. Efimova. - M.: INFRA-M, 2002 ]. O objetivo da análise de regressão é avaliar o valor de uma variável de saída contínua a partir dos valores das variáveis de entrada [
link ].
Deixamos de lado o fato de que a análise de regressão tem à sua disposição dois métodos diferentes - modelagem preditiva e previsão. Observamos apenas que, se houver uma série temporal (dados de séries temporais), usando um modelo de regressão baseado em uma tendência explícita, sujeita à estacionariedade (constância), a previsão poderá ser realizada. Se as condições para a formação de níveis das séries temporais mudarem, ou seja, o processo não estacionário não for observado, então cabe à modelagem preditiva. Particularmente visando o domínio completo da ML, proponho a leitura deste artigo em inglês:
link . Se surgir uma discussão sobre isso, terei prazer em participar.
Como as séries temporais não serão usadas nos exemplos deste artigo, o termo
previsão se refere à
análise preditiva .
Para resolver os problemas de classificação e previsão, é adequado todo um conjunto de algoritmos, alguns dos quais consideraremos mais adiante. Por conveniência, o texto subseqüente será dividido em duas partes: na primeira, consideramos os algoritmos de classificação mais comuns, na segunda, dedicamos aos algoritmos de análise de regressão. Para cada parte, será apresentado um conjunto de dados de "brinquedo" carregado da
biblioteca scikit
-learn (v0.21.3):
conjunto de dados de dígitos (classificação) e
conjunto de dados de preços da casa de Boston (regressão) , bem como links para cada algoritmo da biblioteca scikit-learn para auto-exame e, possivelmente, estudo.
Todos os exemplos de código são executados no console do
IDE Spyder 3.3.3 no Python 3.7.3.
Problema de classificação
Primeiro, importamos os módulos e funções necessários que usaremos para resolver o problema de classificação de dados:
Faça o download do conjunto de dados 'dígitos' diretamente do
módulo 'sklearn.datasets' :
O IDE Spyder fornece uma ferramenta conveniente "Variable Manager", que é útil em todos os momentos do aprendizado de máquina (pelo menos para mim), como
outros "truques" :
Execute o código. No console "gerenciador de variáveis", clique na variável do
conjunto de dados . O seguinte dicionário é exibido:
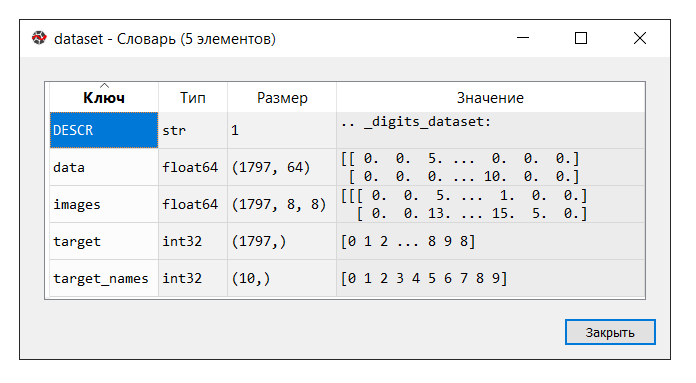
A descrição do conjunto de dados é a seguinte:
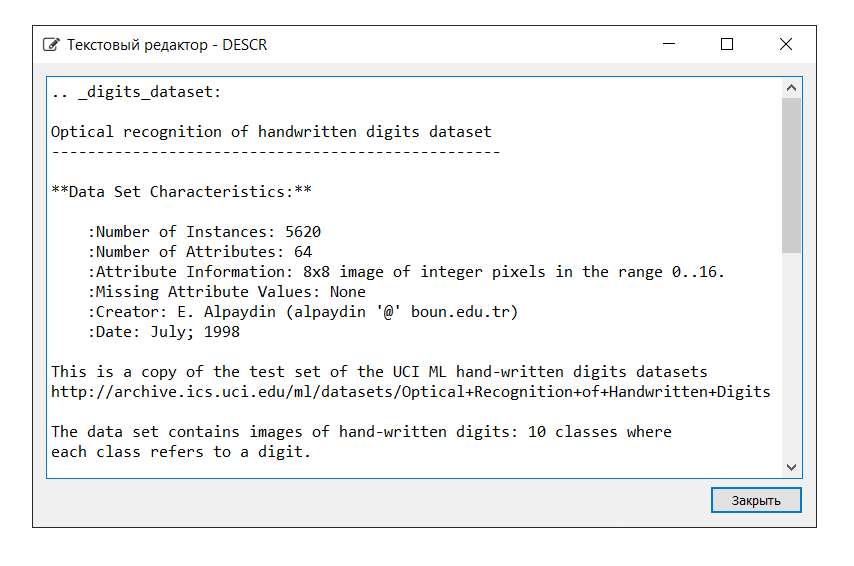
Neste exemplo, não precisamos da chave 'images'; portanto, atribuímos a variável 'data' a
X , que é um array NumPy multidimensional com um conjunto de atributos, 1797 linhas em 64 colunas e a variável
Y a 'target', um array multidimensional NumPy com um marcador para cada string.
Em seguida, dividimos o conjunto de dados nas partes de treinamento e teste, configuramos os parâmetros para avaliar os algoritmos (a validação cruzada é usada [
um ,
dois ]), definindo a 'precisão' da métrica no parâmetro 'scoring' [
link ]. Precisão é a proporção de objetos classificados corretamente em relação ao número total de objetos. Quanto mais próximo o resultado de 1, melhor [
link ]. Além disso, em um dos livros, verificou-se que os resultados de 0,95 (ou 95%) e superiores são considerados excelentes.
Permita que as variáveis
X_train e
Y_train sejam usadas para fins de treinamento,
X_test e
Y_test para o desenvolvimento de valores de previsão. Nesse caso, a variável
Y_test não
está envolvida no cálculo da previsão: usando o método de pontuação, que é o mesmo para cada um dos algoritmos apresentados abaixo, calcularemos as respostas corretas usando a métrica de precisão. Isso nos permitirá julgar como o algoritmo lida com a tarefa. Eu não discuto, por nossa parte, é tão humanamente vil não pedir ao carro as respostas corretas, mas de que outra forma verificar seu desempenho?
Abaixo está uma lista de algoritmos com os quais alimentamos o conjunto de dados. Com base nos resultados dos cálculos, concluiremos qual algoritmo (qual dos algoritmos) mostra a maior eficiência. Esse método pode muito bem ser chamado de
"teste de blitz de algoritmos de aprendizado de máquina" (doravante - teste de blitz).
Por conveniência, as informações serão abreviadas ao lado de cada algoritmo. Deve-se notar que as configurações de cada algoritmo são aceitas por padrão (padrão), com exceção de alguns pontos, a fim de fornecer condições iguais.
Algoritmos lineares:
- Regressão logística * /
Regressão logística ('LR')
* A palavra "regressão" pode ser confusa. Mas não esqueça que "Regressão Logística" é um algoritmo de classificação-
Análise Discriminante Linear ('LDA')
Algoritmos não lineares:
- Método dos k vizinhos mais próximos (classificação) /
K-Neighbors Classifier ('KNN')
-
Classificador da Árvore de Decisão ('CART')
-
Classificador Naive Bayes ('NB')
- Método de
classificação de vetores de suporte linear (classificação) /
Classificação de vetores de suporte linear ('LSVC')
- Método do
vetor de suporte (classificação) /
Classificação do vetor de suporte C ('SVC')
Algoritmo de rede neural artificial:
-
Perceptron multicamada /
Perceptrons multicamada ('MLP')
Algoritmos do conjunto:
- Ensacamento (classificação) /
Classificador de ensacados ('BG') (Ensacamento = agregação de Bootstrap)
-
Classificação florestal aleatória ('RF')
-
Classificador de Árvores Extra ('ET')
- AdaBoost (classificação) /
Classificador AdaBoost ('AB') (AdaBoost = impulso adaptável)
- Reforço de gradiente (classificação) /
Classificador de reforço de gradiente ('GB')
Assim, a lista de 'modelos' contém os seguintes modelos:
models = [] models.append(('LR', LogisticRegression())) models.append(('LDA', LinearDiscriminantAnalysis())) models.append(('KNN', KNeighborsClassifier())) models.append(('CART', DecisionTreeClassifier())) models.append(('NB', GaussianNB())) models.append(('LSVC', LinearSVC())) models.append(('SVC', SVC())) models.append(('MLP', MLPClassifier())) models.append(('BG', BaggingClassifier(n_estimators=n_estimators))) models.append(('RF', RandomForestClassifier(n_estimators=n_estimators))) models.append(('ET', ExtraTreesClassifier(n_estimators=n_estimators))) models.append(('AB', AdaBoostClassifier(n_estimators=n_estimators, algorithm='SAMME'))) models.append(('GB', GradientBoostingClassifier(n_estimators=n_estimators)))
Como já mencionado, a eficácia de cada algoritmo é avaliada usando validação cruzada. Como resultado, uma mensagem é exibida (msg - abreviação de mensagem) contendo as seguintes informações: nome do modelo na forma de uma abreviação, pontuação média de 10 vezes a validação cruzada nos dados de treinamento (métrica 'precisão'), o desvio padrão é mostrado entre parênteses , bem como o valor da métrica "precisão" nos dados de teste.
Depois de executar o código, obtemos os seguintes resultados:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968
Gráfico de amplitude (
“caixa com bigode” ) (diagrama ou plotagem de caixas e bigodes, plotagem de caixas):
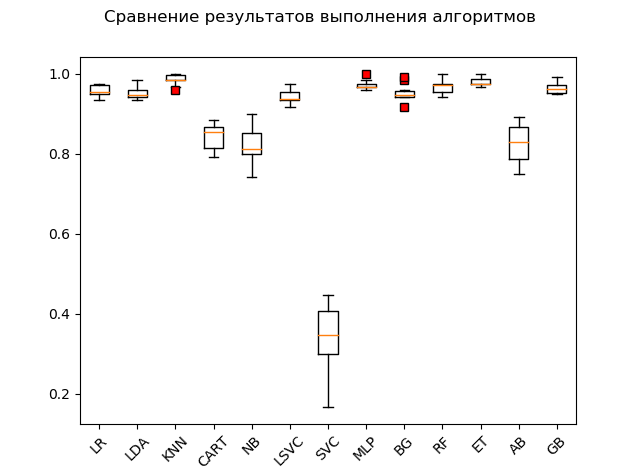
Como resultado de um teste de blitz em dados brutos, pode-se observar que os mais efetivos nos dados de teste foram os algoritmos 'KNN' (k-vizinhos mais próximos), 'ET' (extra-árvores), 'GB' (gradiente 'boosting'), 'RF' (floresta aleatória) e 'MLP' (perceptron multicamada):
KNN: train = 0.985 (0.013) / test = 0.981 ET: train = 0.980 (0.010) / test = 0.975 GB: train = 0.964 (0.013) / test = 0.968 RF: train = 0.968 (0.017) / test = 0.965 MLP: train = 0.972 (0.012) / test = 0.961 LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 BG: train = 0.952 (0.021) / test = 0.941 LSVC: train = 0.942 (0.017) / test = 0.928 CART: train = 0.843 (0.033) / test = 0.830 AB: train = 0.827 (0.049) / test = 0.823 NB: train = 0.819 (0.048) / test = 0.806 SVC: train = 0.343 (0.079) / test = 0.342
No entanto, muitos algoritmos são muito exigentes quanto aos dados em que são veiculados. Portanto, uma das etapas necessárias é a chamada preparação preliminar de dados (pré-processamento de dados [
link ])
No entanto, acontece que o algoritmo mostra os melhores resultados sem processamento preliminar. Daí a seguinte recomendação: inclua no teste de blitz várias transformações do conjunto de dados original e, após realizar os cálculos, compare os resultados para capturar a essência do problema como um todo.
Os métodos mais usados para a preparação preliminar de dados são:
-
padronização;
-
escala (o intervalo padrão é [0, 1]);
-
normalizaçãoEssas operações com avaliação subsequente podem ser automatizadas e colocadas no transportador usando a ferramenta
Pipeline .
Um trecho de código com padronização dos dados de origem é o seguinte:
Observe a adição de '_SS' (abreviação de StandardScaler) para listar nomes. Isso é feito para não acumular os resultados e exibi-los convenientemente usando o "gerenciador de variáveis" após a execução das conversões.
A execução de um trecho de código produz os seguintes resultados:
SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968
Caixa de bigode (StandardScaler):
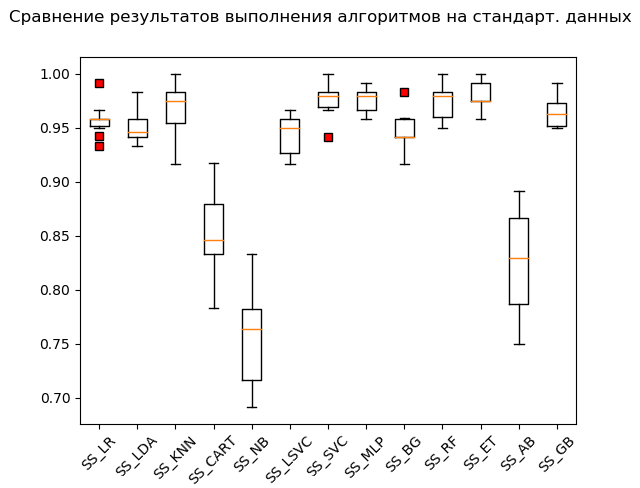
De acordo com os resultados do cálculo em dados padronizados, os seguintes algoritmos se tornaram líderes:
SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_NB: train = 0.756 (0.046) / test = 0.751
Como se costuma dizer, dos trapos às riquezas: o método do vetor de suporte ('SVC'), alimentado por dados padronizados, fez o resto, mostrando um excelente resultado. Durante a verificação “manual”, comparando os valores das variáveis
Y_test e
predictions_SS [6] , o algoritmo não mastigou apenas alguns valores.
A seguir, o mesmo código é executado para as funções MinMaxScaler (dimensionamento) e Normalizador (normalização). Não darei o código completo no artigo. Você pode baixá-lo do meu repositório no GitHub:
link .
Lembre-se de esperar um pouco e rir de si mesmo 'apenas para fins educacionais'! :)
Como resultado, após analisar todo o código, obtemos os seguintes resultados:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968 MMS_LR: train = 0.961 (0.013) / test = 0.953 MMS_LDA: train = 0.951 (0.014) / test = 0.946 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_CART: train = 0.850 (0.027) / test = 0.840 MMS_NB: train = 0.796 (0.045) / test = 0.786 MMS_LSVC: train = 0.964 (0.012) / test = 0.958 MMS_SVC: train = 0.963 (0.016) / test = 0.956 MMS_MLP: train = 0.972 (0.011) / test = 0.963 MMS_BG: train = 0.948 (0.024) / test = 0.946 MMS_RF: train = 0.973 (0.014) / test = 0.968 MMS_ET: train = 0.983 (0.010) / test = 0.981 MMS_AB: train = 0.827 (0.049) / test = 0.823 MMS_GB: train = 0.963 (0.013) / test = 0.968 N_LR: train = 0.938 (0.020) / test = 0.919 N_LDA: train = 0.952 (0.013) / test = 0.949 N_KNN: train = 0.981 (0.012) / test = 0.985 N_CART: train = 0.834 (0.028) / test = 0.825 N_NB: train = 0.825 (0.043) / test = 0.805 N_LSVC: train = 0.960 (0.014) / test = 0.953 N_SVC: train = 0.551 (0.053) / test = 0.586 N_MLP: train = 0.963 (0.018) / test = 0.946 N_BG: train = 0.949 (0.016) / test = 0.938 N_RF: train = 0.973 (0.015) / test = 0.970 N_ET: train = 0.982 (0.012) / test = 0.980 N_AB: train = 0.825 (0.040) / test = 0.820 N_GB: train = 0.953 (0.022) / test = 0.956
Resultados dos "5 principais":
SS_SVC: train = 0.976 (0.015) / test = 0.990 N_KNN: train = 0.981 (0.012) / test = 0.985 KNN: train = 0.985 (0.013) / test = 0.981 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_ET: train = 0.983 (0.010) / test = 0.981
Assim, de acordo com os resultados de um teste de blitz dos algoritmos de aprendizado de máquina para resolver o problema de classificação do conjunto de dados 'dígitos', os algoritmos de aprendizado de máquina mais adequados são: o método k-vizinhos mais próximos ('KNN'), o método do vetor de suporte ('SVC') e extra-árvores («ET»). Esses algoritmos devem prestar mais atenção ao desenvolvimento de resultados que visem aumentar a eficiência dos cálculos. Tudo, como se costuma dizer, é solucionável.
E nesta nota levantada, prossiga sem problemas para a 2ª parte.
Problema de previsão
Passamos o polegar:
Execute o código e lide com o dicionário. Descrição e chaves são as seguintes:
Atribuímos a chave 'data' à variável
X , que é um array NumPy multidimensional com um conjunto de atributos, dimensione 506 linhas por 13 colunas e a variável
Y - 'target', um array NumPy multidimensional com um marcador para cada linha.
Dividimos o conjunto de dados em partes de treinamento e teste, configuramos os parâmetros para avaliar os algoritmos. No parâmetro 'scoring', definimos uma das
métricas 'r2' tradicional para análise de regressão:
R2 - coeficiente de determinação - é a proporção da variância da variável dependente, explicada pelo modelo em questão (
link ).
“O coeficiente de determinação para um modelo com uma constante leva valores de 0 a 1. Quanto mais próximo o coeficiente de 1, maior a dependência. Ao avaliar modelos de regressão, isso é interpretado como correspondendo o modelo aos dados. Para modelos aceitáveis, assume-se que o coeficiente de determinação deve ser de pelo menos 50% (neste caso, o coeficiente de correlação múltipla excede o módulo de 70%). Modelos com um coeficiente de determinação acima de 80% podem ser considerados bastante bons (o coeficiente de correlação excede 90%). A igualdade do coeficiente de determinação com a unidade significa que a variável explicada é exatamente descrita pelo modelo em consideração ” (ibid.).
Para resolver o problema de previsão, usamos os seguintes algoritmos:
Algoritmos lineares:
-
Regressão linear ('LR')
- Regressão de Ridge (regressão de
Ridge ) /
Regressão de Ridge ('R')
- Regressão do laço (do inglês LASSO - Operador de Seleção e Retração Menos Absolutos) /
Regressão do laço ('L')
- Método de regressão de
regressão líquida elástica ('ELN')
- Método da
regressão com ângulo mínimo (LARS) ('LARS')
- Regressão da crista bayesiana / regressão da crista
bayesiana ('BR')
Algoritmos não lineares:
-
método k-regressor de vizinhos mais próximos ('KNR')
-
Regressor da árvore de decisão ('DTR')
-
Máquina de vetores de suporte linear (regressão) /
Máquina de vetores de suporte linear - regressão / ('LSVR')
- Método do
vetor de suporte (regressão) /
regressão do vetor de suporte Epsilon ('SVR')
Algoritmos do conjunto:
- AdaBoost (regressão) /
AdaBoost Regressor ('ABR') (AdaBoost = reforço adaptativo)
- Ensacamento (regressão) /
Regressor de ensacamento ('BR') (Ensacamento = agregação de Bootstrap)
-
Regressor de árvores extras ('ETR')
- Reforço de gradiente (regressão) /
Regressor de reforço de gradiente ('GBR')
-
Classificação aleatória de floresta (regressão) /
classificador aleatório de floresta ('RFR')
Assim, a lista de 'modelos' contém os seguintes modelos:
models = [] models.append(('LR', LinearRegression())) models.append(('R', Ridge())) models.append(('L', Lasso())) models.append(('ELN', ElasticNet())) models.append(('LARS', Lars())) models.append(('BR', BayesianRidge(n_iter=n_iter))) models.append(('KNR', KNeighborsRegressor())) models.append(('DTR', DecisionTreeRegressor())) models.append(('LSVR', LinearSVR())) models.append(('SVR', SVR())) models.append(('ABR', AdaBoostRegressor(n_estimators=n_estimators))) models.append(('BR', BaggingRegressor(n_estimators=n_estimators))) models.append(('ETR', ExtraTreesRegressor(n_estimators=n_estimators))) models.append(('GBR', GradientBoostingRegressor(n_estimators=n_estimators))) models.append(('RFR', RandomForestRegressor(n_estimators=n_estimators)))
Como na classificação, a avaliação da eficácia de cada algoritmo é feita usando a validação cruzada. A mensagem exibida contém as seguintes informações: o nome do modelo na forma de uma abreviação, a pontuação média de uma validação cruzada de 10 vezes nos dados de treinamento (métrica 'r2'), o desvio padrão e o coeficiente de determinação r2 nos dados de teste são mostrados entre colchetes.
Depois de executar o código, obtemos os seguintes resultados:
LR: train = 0.746 (0.068) / test = 0.579 R: train = 0.744 (0.067) / test = 0.570 L: train = 0.689 (0.070) / test = 0.641 ELN: train = 0.677 (0.074) / test = 0.662 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 KNR: train = 0.434 (0.288) / test = 0.538 DTR: train = 0.671 (0.145) / test = 0.637 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003 ABR: train = 0.810 (0.078) / test = 0.763 BR: train = 0.854 (0.064) / test = 0.805 ETR: train = 0.889 (0.047) / test = 0.836 GBR: train = 0.878 (0.042) / test = 0.863 RFR: train = 0.852 (0.068) / test = 0.819
Gráfico de amplitude:
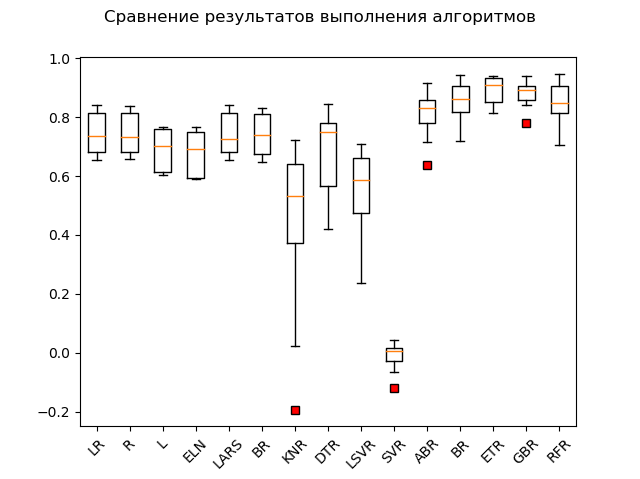
Os líderes óbvios são os métodos de conjunto 'GBR' (gradiente 'reforço'), 'ETR' (extra-árvores), 'RFR' (floresta aleatória) e 'BR' ('ensacamento'):
GBR: train = 0.878 (0.042) / test = 0.863 ETR: train = 0.889 (0.047) / test = 0.836 RFR: train = 0.852 (0.068) / test = 0.819 BR: train = 0.854 (0.064) / test = 0.805 ABR: train = 0.810 (0.078) / test = 0.763 ELN: train = 0.677 (0.074) / test = 0.662 L: train = 0.689 (0.070) / test = 0.641 DTR: train = 0.671 (0.145) / test = 0.637 LR: train = 0.746 (0.068) / test = 0.579 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 R: train = 0.744 (0.067) / test = 0.570 KNR: train = 0.434 (0.288) / test = 0.538 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003
Um "adabust", "loshara", fica para trás.
Talvez os três líderes estejam combatendo a padronização e a normalização. Vamos descobrir executando o restante do código.
Os resultados são os seguintes:
SS_LR: train = 0.746 (0.068) / test = 0.579 SS_R: train = 0.746 (0.068) / test = 0.578 SS_L: train = 0.678 (0.054) / test = 0.510 SS_ELN: train = 0.665 (0.060) / test = 0.513 SS_LARS: train = 0.744 (0.069) / test = 0.579 SS_BR: train = 0.746 (0.066) / test = 0.576 SS_KNR: train = 0.763 (0.098) / test = 0.739 SS_DTR: train = 0.610 (0.242) / test = 0.629 SS_LSVR: train = 0.727 (0.091) / test = 0.482 SS_SVR: train = 0.653 (0.126) / test = 0.610 SS_ABR: train = 0.811 (0.076) / test = 0.819 SS_BR: train = 0.853 (0.074) / test = 0.813 SS_ETR: train = 0.887 (0.048) / test = 0.846 SS_GBR: train = 0.878 (0.038) / test = 0.860 SS_RFR: train = 0.851 (0.071) / test = 0.818 N_LR: train = 0.751 (0.099) / test = 0.576 N_R: train = 0.287 (0.126) / test = 0.271 N_L: train = -0.030 (0.032) / test = -0.000 N_ELN: train = -0.007 (0.030) / test = 0.023 N_LARS: train = 0.751 (0.099) / test = 0.576 N_BR: train = 0.744 (0.100) / test = 0.589 N_KNR: train = 0.485 (0.192) / test = 0.504 N_DTR: train = 0.729 (0.080) / test = 0.765 N_LSVR: train = 0.182 (0.108) / test = 0.136 N_SVR: train = 0.086 (0.076) / test = 0.084 N_ABR: train = 0.795 (0.053) / test = 0.752 N_BR: train = 0.854 (0.054) / test = 0.827 N_ETR: train = 0.877 (0.048) / test = 0.850 N_GBR: train = 0.852 (0.063) / test = 0.872 N_RFR: train = 0.852 (0.051) / test = 0.801
Como você pode ver, os métodos de conjunto ainda estão à frente de todos.'Top 5' contém os seguintes resultados: N_GBR: train = 0.852 (0.063) / test = 0.872 GBR: train = 0.878 (0.042) / test = 0.863 SS_GBR: train = 0.878 (0.038) / test = 0.860 N_ETR: train = 0.877 (0.048) / test = 0.850 SS_ETR: train = 0.887 (0.048) / test = 0.846
Vamos exibir um gráfico comparando os resultados: o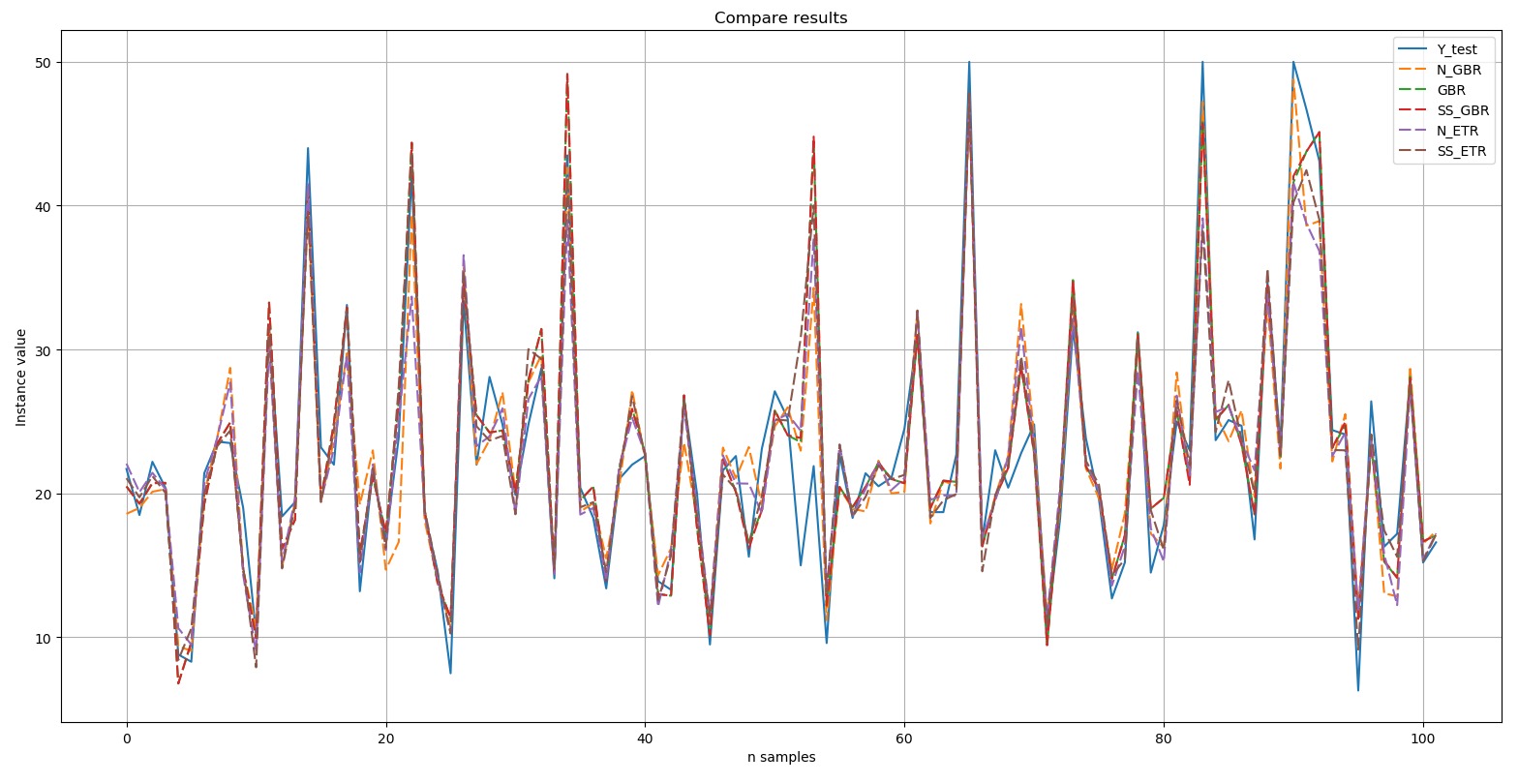
teste Y é o padrão. Os cinco resultados selecionados mostrados no diagrama são indicados por uma linha tracejada. Pode-se observar que todos os picos foram reproduzidos com repetição exata ou em um grau ou outro.Trecho curto da comparação manual dos valores de referência e dos valores de previsão do algoritmo incluído no Top 5:
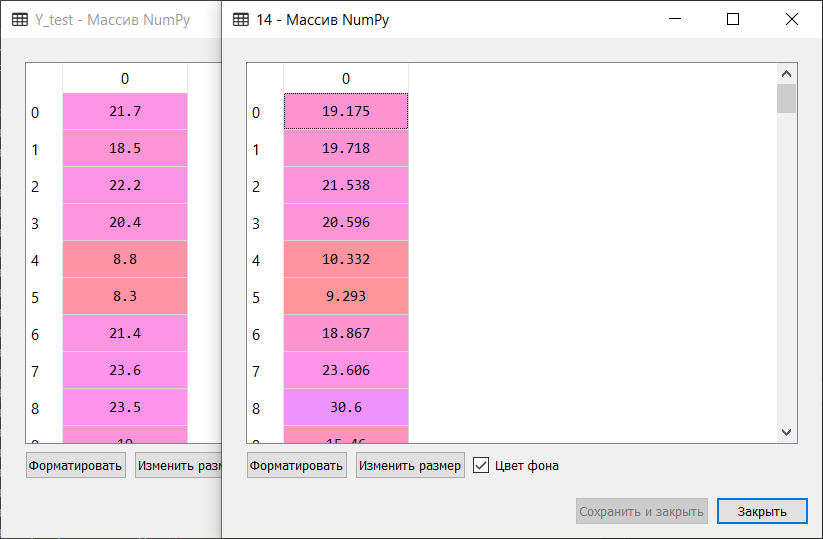Assim, de acordo com os resultados de um teste de blitz de algoritmos de aprendizado de máquina para resolver o problema de prever o conjunto de dados 'preço da casa de boston', os algoritmos mais adequados são o “impulso” de gradiente ('GBR ') e árvores extras (' ETR '). Esses algoritmos devem receber mais atenção para desenvolver ainda mais os resultados e aumentar a eficácia das previsões.Posfácio
Uma verificação rápida dos algoritmos de aprendizado de máquina permite, em uma primeira aproximação, identificar os algoritmos mais eficazes para resolver problemas de classificação e análise de regressão (previsão). Ficamos convencidos disso processando o conjunto de dados 'dígitos', classificando de forma brilhante as instâncias em 10 classes, bem como o conjunto de dados 'preço da casa de boston', classificando de maneira "surpreendente" a localização de dependências e a previsão "flutuante" da variável dependente.Você está convidado a experimentar esse método em seus próprios conjuntos de dados ou naqueles que você pode cavar em vários repositórios, incluindo o GitHub. Por exemplo: link .Obtenha um conjunto de dados adequado para o alvo - e defina um monte de algoritmos nele na equipe do teste de blitz. E aí fica claro de quem é: quem está no campo não é um guerreiro. :)
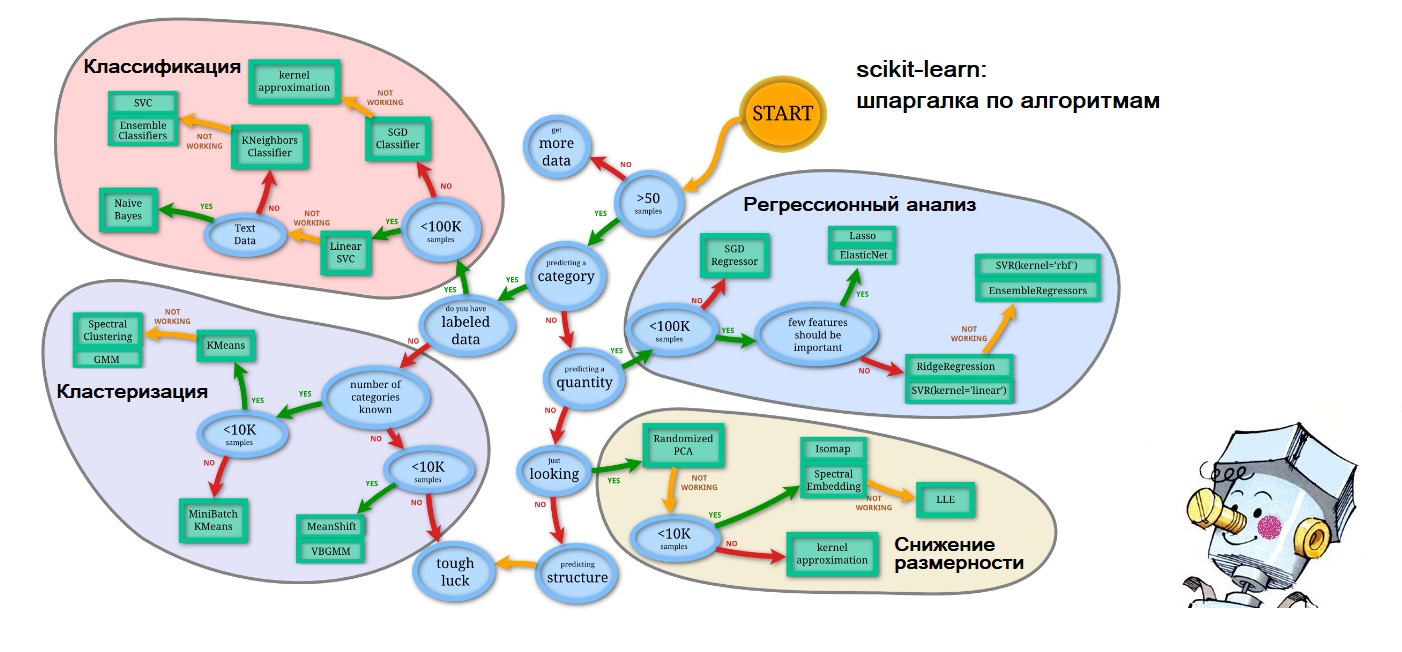
E em conclusão. Serei grato por seus comentários, perguntas e sugestões, pois a base deste artigo é a informação que compartilho com novos colegas em cada novo projeto no campo de aprendizado de máquina. Cada um deles tem sua própria especialização, sobre aprendizado de máquina e redes neurais artificiais, muitos deles apenas "ouvidos em algum lugar", por isso é importante para mim falar sobre complexos, multifacetados e, finalmente, inexpugnáveis (trata-se de RNA e aprendizado de máquina em geral) :), em uma linguagem simples e compreensível; mostre que não são os deuses que queimam panelas; e que, se houver interesse, mais de uma dúzia de algoritmos podem ser "aproveitados". :)
PS No final do artigo, comecei a me prever, então, para as próximas perguntas sobre onde obtive as dicas na primeira figura que forneço: tudo no mesmo site scikit-learn.org ( 'Escolhendo o estimador certo' ): link . E a personificação da inteligência artificial na forma de um Samodelkin corado é assim das ondas de memória da minha infância feliz.