A hipótese dos gêmeos primos é uma das questões mais importantes e complexas da matemática. Dois matemáticos resolveram uma versão paralela desse problema para pequenos sistemas numéricos.

Em 7 de setembro, dois matemáticos
publicaram uma prova de uma versão de um dos problemas abertos mais famosos da matemática. O resultado abre uma nova frente no estudo da hipótese de
primos gêmeos que atormenta os matemáticos há mais de cem anos e está associada a algumas das propriedades mais profundas da aritmética.
"Estamos derrapando há muito tempo e estamos ficando sem ideias para essa tarefa, por isso é natural que alguém tenha novas idéias", disse
James Maynard , matemático de Oxford.
A hipótese de gêmeos primos se aplica a pares de números primos que diferem por 2. Os gêmeos são os números 5 e 7. E 17 e 19. A hipótese afirma que existe um número infinito desses pares entre os números naturais. Na última década, os matemáticos fizeram um progresso significativo, mas ainda estão muito longe de uma solução completa para o problema.
Os autores da nova evidência,
Will Savin, da Columbia University, e
Mark Shusterman, da University of Wisconsin, em Madison, provaram a hipótese de um mundo matemático menor, mas ainda perceptível. Eles provaram sua validade no caso de um sistema numérico finito no qual existem apenas alguns números.
Esses sistemas numéricos são chamados de "campos finitos". Apesar do tamanho pequeno, eles retêm muitas das propriedades matemáticas inerentes a inúmeros números inteiros. Os matemáticos estão tentando encontrar respostas para questões de aritmética em campos finitos e esperam traduzir esses resultados para todos os números inteiros.
"O sonho final, embora um pouco ingênuo, é que um bom entendimento das propriedades de um campo finito possa lançar luz sobre o mundo dos números inteiros", disse Maynard.
Além de provar a hipótese dos primos gêmeos, Savin e Shusterman encontraram um resultado ainda mais surpreendente em relação ao comportamento dos primos em pequenos sistemas numéricos. Eles provaram a frequência exata com que primos gêmeos aparecem em pequenos intervalos - e esse resultado torna possível controlar com extrema precisão um fenômeno como os primos gêmeos. Os matemáticos sonham em alcançar resultados semelhantes com números comuns; eles exploram novas evidências em busca de idéias aplicáveis aos números primos em uma linha numérica.
Um novo tipo de prime
A previsão mais famosa da hipótese dos gêmeos primos é a presença de um número infinitamente grande de pares de números que diferem por 2. No entanto, essa afirmação é mais geral. Ele diz que há um número infinito de números primos que diferem em 4 (por exemplo, 3 e 7), ou em 14 (293 e 307) ou em qualquer número que você especificar.
Alfons de Polignac
fez essa suposição em sua forma moderna em 1849. Nos 160 anos seguintes, os matemáticos não avançaram muito com ele. No entanto, em 2013, o gelo quebrou, ou pelo menos seriamente quebrou. Naquele ano,
Zhang Ethan provou a presença de um número infinitamente grande de pares de números primos, diferindo em não mais de 70 milhões.No próximo ano, outros matemáticos, incluindo Maynard e
Terry Tao , reduziram seriamente essa lacuna. O registro atual é a prova da existência de um número infinitamente grande de pares de números primos que diferem entre si em não mais que 246.
No entanto, depois disso, o progresso diminuiu. Os matemáticos entendem a necessidade de uma idéia completamente nova para resolver completamente esse problema. E sistemas de números finitos são um bom lugar para procurar essa idéia.
Para criar um campo finito, você primeiro precisa extrair um subconjunto finito de números dos números naturais. Você pode, por exemplo, pegar os cinco primeiros números (ou qualquer número primo). E, em vez de representar números em uma linha numérica, como sempre, imagine um novo sistema numérico na forma de um mostrador.
A aritmética, como você deve ter adivinhado, começa a trabalhar em um espaço confinado. O que serão 4 + 3 em um sistema numérico finito constituído por cinco elementos? Começamos com 4, contamos três divisões no sentido horário e chegamos a 2. Subtração, multiplicação e divisão funcionam de maneira semelhante.

Mas só há um problema. Em campos finitos, a definição usual de primo não faz sentido. No campo final, qualquer número é dividido por qualquer outro. Por exemplo, 7 geralmente não é divisível por 3. Mas em um campo final de cinco elementos, é divisível. Isso porque nesse campo final o número 7 é equivalente ao número 12 - ambos terminam na marca 2 do mostrador. Portanto, 7 dividido por 3 dará o mesmo que 12 dividido por 3 - e 12 dividido por 3 dará 4.
Portanto, a hipótese de primos gêmeos para campos finitos refere-se a polinômios simples - expressões matemáticas como, por exemplo, x
2 + 1.
Suponha, por exemplo, que seu campo final contenha os números 1, 2 e 3. Esses números serão os coeficientes do polinômio nesse campo finito e o polinômio "simples" será aquele que não pode ser decomposto em fatores polinomiais. Portanto, x
2 + x + 2 será simples, pois não pode ser fatorado, mas x
2 - 1 não: este é o produto de (x + 1) e (x - 1).
Tendo definido polinômios simples, é natural fazer uma pergunta sobre polinômios gêmeos simples - pares de polinômios que são simples e diferem por um valor fixo. Por exemplo, o polinômio x
2 + x + 2 é simples, como x
2 + 2x + 2. Eles diferem por x.
A hipótese de polinômios gêmeos simples para campos finitos indica a existência de um número infinitamente grande de pares de polinômios gêmeos simples que diferem não apenas por x, mas por qualquer valor.
Cortes perfeitos
Os conceitos de campos finitos e polinômios simples podem parecer absurdos e inúteis para o estudo das propriedades dos números. Mas eles parecem um simulador de furacões - um universo em si, dando idéias sobre fenômenos que ocorrem em um grande mundo.
"Existe uma analogia antiga entre números inteiros e polinômios, que permite converter problemas potencialmente extremamente complexos relacionados a números inteiros em tarefas relacionadas a polinômios, que também são potencialmente complexos, mas podem ser mais fáceis de resolver", disse Shusterman.
Os campos finitos tornaram-se famosos em 1940, quando
Andre Weil desenvolveu a maneira exata de traduzir a aritmética de pequenos sistemas numéricos na aritmética de números inteiros. Weil usou essa conexão com resultados surpreendentes. Ele
provou , talvez, o problema mais importante da matemática - a hipótese de Riemann - para o caso de um conjunto de curvas sobre campos finitos (esse problema é conhecido pelo nome da hipótese geométrica de Riemann). Essa prova, juntamente com um conjunto de
hipóteses adicionais de
Weyl, tornou os campos finitos um rico cenário para descobertas matemáticas.
A idéia principal de Weil era que, em campos finitos, técnicas geométricas podem ser usadas para encontrar respostas para perguntas sobre números. “Essa é uma característica dos campos finitos. Muitas das tarefas que você deseja resolver podem ser reformuladas geometricamente ”, disse Shusterman.
Para entender como a geometria aparece em um ambiente como esse, imagine cada polinômio como um ponto no espaço. Os coeficientes de um polinômio servem como coordenadas para determinar sua localização. Retornando ao nosso campo final de 1, 2 e 3, o polinômio 2x + 3 está localizado no ponto (2, 3) do espaço bidimensional.
Mas mesmo no espaço finito mais simples, há um número infinito de polinômios. Polinômios mais complexos podem ser criados aumentando o expoente do maior expoente ou grau de expressão. No nosso caso, o polinômio x
2 - 3x - 1 será representado por um ponto no espaço tridimensional. E o polinômio 3x
7 + 2x
6 + 2x
5 - 2x
4 - 3x
3 + x
2 - 2x + 3 será representado por um ponto no espaço oito-dimensional.
No novo trabalho, esse espaço geométrico representa todos os polinômios de um determinado grau para um determinado campo finito. A questão se transforma no seguinte: existe uma maneira de isolar todos os pontos que denotam polinômios simples?
A estratégia de Savin e Shusterman é dividir o espaço em duas partes. Em uma parte, haverá todos os pontos correspondentes a polinômios com um número par de fatores. No outro, todos os pontos correspondentes a polinômios com um número ímpar de fatores.
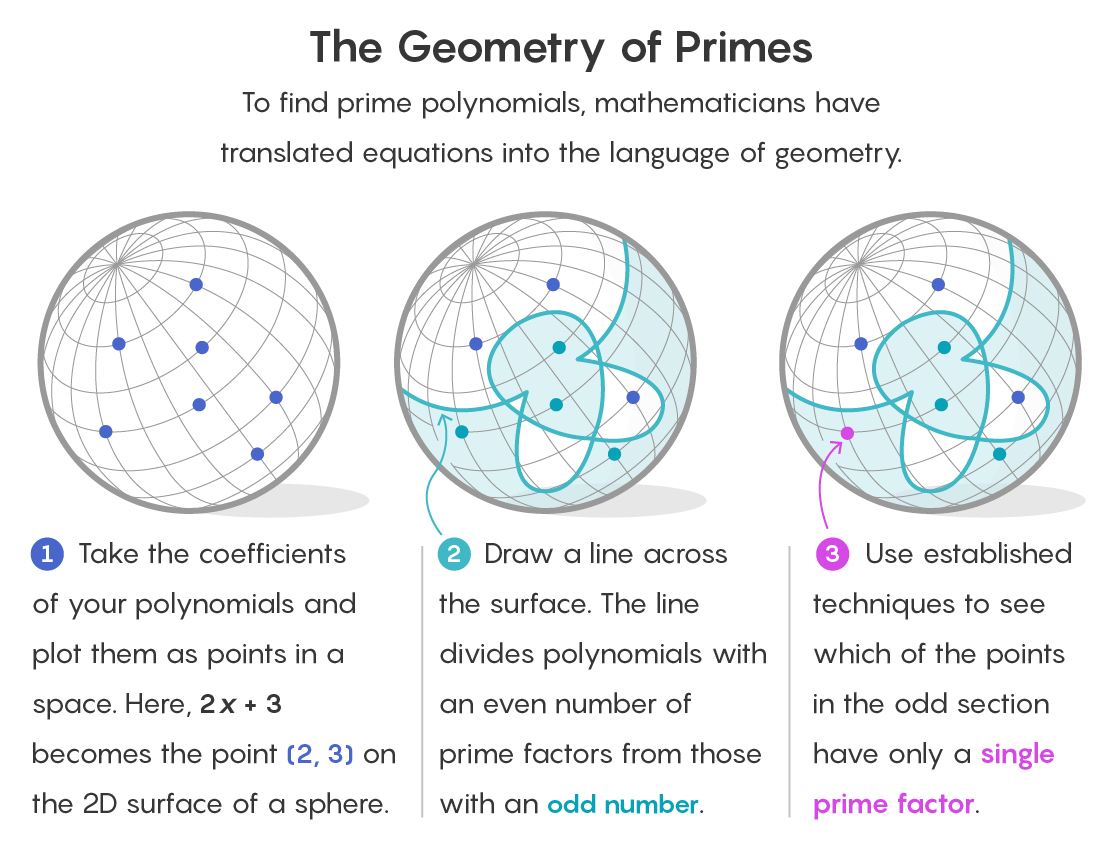
Isso já simplifica a tarefa. A hipótese de polinômios gêmeos simples para campos finitos se aplica somente a polinômios com um fator (assim como um primo tem um fator, ele próprio). E como o número 1 é ímpar, parte do espaço que contém polinômios com um número par de fatores pode ser imediatamente descartado.
O truque é usar a divisão. No caso de um objeto bidimensional, por exemplo, a superfície de uma esfera, ele é cortado pela metade por uma curva unidimensional - assim como o equador corta a superfície da Terra. Um objeto com um grande número de dimensões sempre pode ser cortado com um objeto com o número de dimensões menor que um.
Mas essas formas com menos dimensões, dividindo o espaço dos polinômios, não são tão elegantes quanto o equador. Eles são desenhados de acordo com uma fórmula matemática chamada
função Mobius . Na entrada, é necessário um polinômio e, na saída, fornece 1 se o polinômio tiver um número par de fatores primos, -1 se tiver um número ímpar e 0 se for fatorado (já que 16 pode ser dividido por 2 × 2 × 2 × 2).
As curvas desenhadas pela função Mobius dobram e torcem como loucas, cruzando-se em muitos lugares. Esses lugares, chamados singularidades, são especialmente difíceis de analisar (eles correspondem a polinômios que podem ser decompostos em vários fatores primos idênticos).
A inovação fundamental de Savin e Shusterman foi que eles encontraram a maneira exata de cortar loops com menos medições em segmentos mais curtos. Esses segmentos foram mais fáceis de aprender do que todo o ciclo.
Tendo compilado um catálogo de polinômios com um número ímpar de fatores primos - e este foi o mais difícil - Savin e Shusterman enfrentaram a tarefa de determinar quais são simples e quais são gêmeos. Para fazer isso, eles aplicaram várias fórmulas usadas pelos matemáticos para estudar números primos entre os comuns.
Savin e Shusterman usaram sua técnica para provar dois pontos importantes sobre polinômios simples em certos campos finitos.
Primeiro, a hipótese de números primos gêmeos em campos finitos é verdadeira: existem infinitamente muitos pares de polinômios gêmeos que diferem por qualquer valor.
Em segundo lugar, e mais importante, este trabalho fornece uma contagem precisa do número de polinômios gêmeos simples que podem ser encontrados entre polinômios de uma determinada ordem. Isso é análogo a saber quantos primos gêmeos estão dentro de qualquer intervalo suficientemente longo em uma linha numérica - e este é apenas o sonho dos matemáticos.
"Este é o primeiro trabalho que fornece uma analogia quantitativa do que deve ser verdadeiro para números inteiros, e este é um resultado realmente notável", disse Ziv Rudnik, da Universidade de Tel Aviv. "Até agora, nada disso aconteceu."
A prova de Savin e Schusterman mostra como, quase 80 anos depois de Andre Weil provar a hipótese de Riemann para curvas em campos finitos, os matemáticos ainda seguem teimosamente nessa direção. Agora, os matemáticos que lidam com a hipótese dos gêmeos primos se voltarão para o trabalho de Savin e Shusterman, e talvez isso lhes dê uma fonte profunda de inspiração.