Qual é o próximo membro ...? - Estamos procurando uma fórmula para o enésimo termo da sequência, gerando funções e transformação Z

Você pode baixar o arquivo com o código e os dados na postagem original no meu blog

A Wolfram Language possui quatro recursos totalmente impressionantes: FindSequenceFunction , RSolve , DifferenceRootReduce e FindFormula . Neste artigo, discutiremos seus recursos e falaremos sobre as funções que estão intimamente relacionadas a eles - para procurar FindLinearRecurrence recursão linear FindLinearRecurrence (coeficientes de uma equação de recorrência linear) que geram as ZTransform transformação Z GeneratingFunction e ZTransform .

A primeira função , FindSequenceFunction, procura uma expressão para seu enésimo membro por uma sequência de números sem exigir mais nada.

 Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n] 

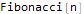
 FindSequenceFunction[ {-2, 4Sqrt[Pi], -16, 16Sqrt[Pi], -128/3, 32Sqrt[Pi], -1024/15, 128Sqrt[Pi]/3, -8192/105, 128Sqrt[Pi]/3}, n] 

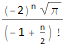A segunda função , RSolve, resolve equações de recorrência de vários tipos. Os elementos podem parecer $$$a [f [n]]$, $$$a [f [f [n]]]$, $$$a [f [f [\ texto {...} f [n] \ texto {...}]]]$, onde f tem a forma: n + A (equações da diferença aritmética), B * n - equações geométricas ou da diferença q), B * n + a (equações da diferença funcional aritmético-geométrica), B * n ^ d (função geométrica da potência equações da diferença), (A * n + B) / (C * n + D) (equações da diferença funcional fracionária linear).

 RSolve[ { a[n + 3]==2 * a[n], a[1]==α, a[2]==β, a[3]==γ }, a, n ] 

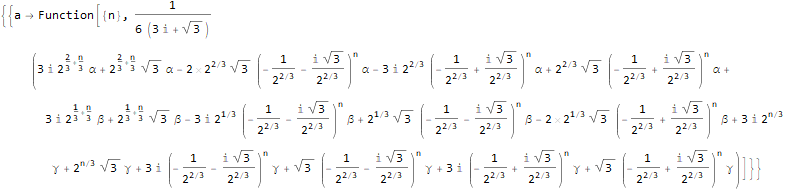
 RSolve[ { v[n]==(2 * Pi * v[n - 2]) / n, v[2]==Pi, v[3]==(4 * Pi) / 3 }, v @ n, n ] 

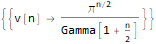A terceira função - DifferenceRootReduce - procura por uma relação de recorrência para uma sequência de números, cujo enésimo membro possui uma determinada forma.

 DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1], n ] 

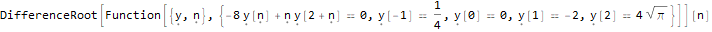
 RSolve[ { (-8 * y[n]) + n * y[2 + n]==0, y[-1]==1/4, y[0]==0, y[1]==-2, y[2]==4Sqrt[Pi] }, y, n ] 

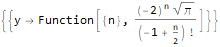
Essa função pode fazer muito mais, digamos, verificar identidades com relação às sequências, por exemplo:

 DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n] 

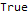
Aqui, LucasL é uma sequência de números Luc (na verdade, é uma sequência de Fibonacci, apenas os primeiros membros não são 1, 1, mas 1, 3.

 Hold @ DifferenceRootReduce @ LucasL @ n 

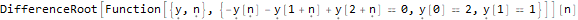
 DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]] 

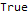
Como encontrar uma fórmula de recorrência para uma sequência?

O método de pesquisa para um membro comum de uma sequência geralmente é baseado na necessidade de selecionar uma equação de recorrência.

Pode funcionar assim: vamos procurar o enésimo membro da sequência no formato $$$f [n] = \ sum_ {i = 1} ^ ka [i] f [n-i]$. Vamos ter os primeiros membros da sequência:

 sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461} 

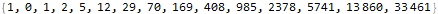
Vamos tentar encontrar uma expressão para o enésimo termo no formulário $$$f [n] = \ sum_ {i = 1} ^ 1a [i] f [n-i] = a [1] f [n-1]$:

 seauenseEq1 = MovingMap[ Function[ Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1] ], sequence, 1 ] 

 Hold @ Solve @ seauenseEq1 

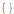
Como você pode ver, não há soluções.

Vamos tentar pesquisar agora no formulário $$$f [n] = \ sum_ {i = 1} ^ 2a [i] f [n-i] = a [1] f [n-1] + a [2] f [n-2]$:

 seauenseEq2 = MovingMap[ Function[ Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1] ], sequence, 2 ] 

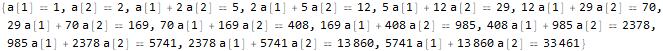
 Hold @ Solve @ seauenseEq2 

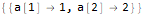
Como vemos, acabou. Portanto, o enésimo termo tem a forma: $$$f [n] = f [n-1] + 2f [n-2]$.

Na verdade, existe uma função FindLinearRecurrence que permite encontrar recursão linear, semelhante à maneira como fizemos:

 Hold @ FindLinearRecurrence @ sequence 

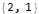
Usando a função LinearRecurrence , LinearRecurrence pode estender a sequência:

 LinearRecurrence[{2, 1}, sequence[[1;;2]], 50] 

Ou combine tudo em uma linha, construindo uma função que: estenda a sequência, produza uma equação de diferença e encontre uma fórmula geral para o enésimo termo:

 sequenseExtension[list_, n_] := Module[ {lr, eq}, lr = FindLinearRecurrence @ list; eq = Flatten[ { a[k]==Total[ Table[ a[k + -i] * Part[lr, i], {i, 1, Length @ lr} ] ], Table[a[i], list[[i]]], {i, 1, Length @ lr}] } ]; <| "" -> eq, "" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]], "" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n] |> ]; 

 Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20] 

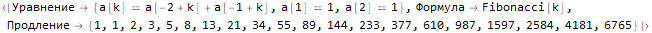
 Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20] 

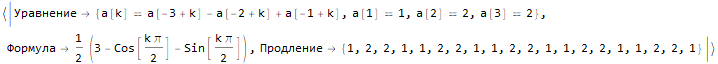
 Hold @ sequenseExtension[ {1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4}, 25 ] 

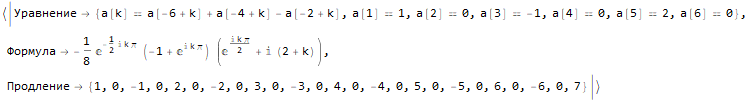
Como encontrar a fórmula para o enésimo membro de uma sequência?

Conversão Z

A transformação Z consiste em calcular uma série da forma $$$\ sum_ {n = 0} ^ {\ infty} f (n) z ^ {- n}$de função discreta $$$f (n)$. Essa transformação nos permite reduzir a equação de recorrência para definir a sequência na equação da imagem da função $$$f (n)$, que é semelhante à transformada de Laplace, que reduz as equações diferenciais às algébricas.

Veja como funciona:

 Grid[ Transpose[ Function[ { #, Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]] } ][ { f[n - 2], f[n - 1], f @ n, f[n + 1], f[n + 2] } ] ], Background -> White, Dividers -> All ] 

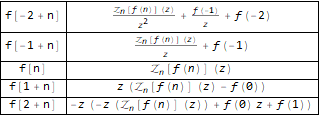
Vejamos um exemplo, digamos, pegue a conhecida sequência de Fibonacci:

 fibonacciEq = f[n]==f[n - 1] + f[n - 2]; initialConditions = {f[1] -> 1, f[2] -> 1}; 

É claro que ele deve ser reescrito no formulário, como mostrado abaixo, para que construções como $$$f (-1)$depois de aplicar a transformação Z.

 fibonacciEq = f[n + 2]==f[n + 1] + f[n]; initialConditions = {f[0] -> 1, f[1] -> 1}; 

Realizamos a transformação Z:

 fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]] 

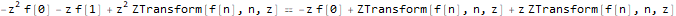
Resolvemos a equação para a imagem da função f - ZTransform [f [n], n, z]:

 fZTransformed = ReplaceAll[ ZTransform[f @ n, n, z], Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1] ] 

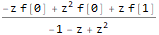
Realizamos a transformação Z inversa, substituindo as condições iniciais ao mesmo tempo (substituímos n por n-1 na expressão final para que nossa sequência tenha a indexação correta (do primeiro, não do termo zero):

 ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n], n -> (n - 1) ] 

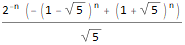
Naturalmente, isso pode ser automatizado criando sua própria contraparte do RSolve:

 myRSolve[eq_, initials_, f_, n_] := Module[ {z, initialsInner, eqZTransformed, fZTransformed}, initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]]; eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]]; fZTransformed = ReplaceAll[ZTransform[f @ n, n, z], Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1] ]; FullSimplify[ InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1) ] ]; 

 myRSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]) }, {f[1] -> 20, f[2] -> 0}, f, n ] 

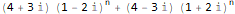
 RSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]), f[1]==20, f[2]==0 }, f, n ] 

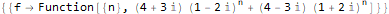
Mas, é claro, o RSolve contém muito mais possibilidades para resolver uma grande variedade de equações discretas, nas quais não iremos nos aprofundar mais detalhadamente:

 RSolve[a[n]==(n * a[n]) + n, a, n], RSolve[ { a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4, a[0]==0 }, a, n ], RSolve[ y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2, y, n ] 

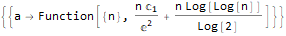
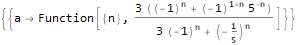
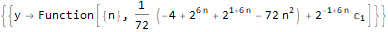
Gerando funções

Gerando função de sequência $$$a (n)$essa é uma função $$$G (x)$, cuja expansão na série Taylor (ou, mais amplamente, Laurent) tem a forma - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} a (n) x ^ n$. Em outras palavras, os coeficientes de potências de x na expansão da função em uma série determinam nossa sequência.

Função Say $$$G (x) = \ frac {1} {1-x}$é uma função geradora da sequência 1, 1, 1, 1, ...:

 Series[1 / (1 + -x), {x, 0, 10}] 

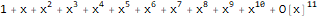
Uma função $$$G (x) = \ frac {1} {1-x-x ^ 2}$é uma função geradora da sequência de Fibonacci 1, 1, 2, 3, 5, 8, 13, ...:

 Series[(1 * 1) + (-x) + -(x * 2), {x, 0, 10} ] 

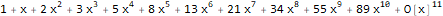
Há também um tipo de função geradora - uma função geradora exponencial, que para a sequência $$$a (n)$tem a forma - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} \ frac {a (n)} {n!} X ^ n$.

Digamos, para as seqüências 1, 1, 1, 1 ... e 1, 1, 2, 3, 5, 8, 13, ... as funções geradoras exponenciais são as seguintes - $$$e ^ x$e $$$\ frac {1} {\ sqrt {5}} e ^ {- \ frac {2x} {1+ \ sqrt {5}}} \ left (e ^ {\ sqrt {5} x} -1 \ right)$:

 ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

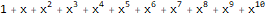
 ReplaceAll[ Normal[ FullSimplify[ Series[ Plus[E, (-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5 ], {x, 0, 10} ] ] ], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

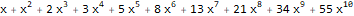
A função de produção na Wolfram Language pode ser encontrada por duas funções - GeneratingFunction e FindGeneratingFunction (exponencial com ExponentialGeneratingFunction ):

 GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}] 

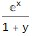
 TraditionalForm[ FullSimplify[ ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x] ] ] 

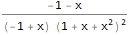
Existem muitos métodos para encontrar um membro comum de uma sequência usando funções geradoras. Não vamos nos aprofundar nisso em detalhes, digamos, apenas uma boa teoria está no site genfunc.ru .

Um dos métodos é semelhante à transformação Z:

 generatingFEq = ReplaceAll[ f[n + 2]==f[n + 1] + f[n], pattern:f[__] :> GeneratingFunction[pattern, n, z] ], generatingF = ReplaceAll[ GeneratingFunction[f @ n, n, z], Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1] ], nthTerm = SeriesCoefficient[generatingF, {z, 0, n}], FullSimplify[ ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}], n -> (n - 1) ], GreaterEqual[n, 1] ] 

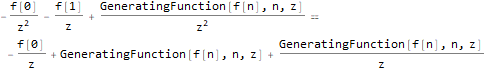
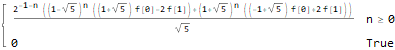
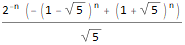
OEIS - Enciclopédia de sequência inteira on-line e integração com a Wolfram Language

Uma coleção absolutamente impressionante de sequências numéricas está disponível na Internet - OEIS (Enciclopédia On-Line de Sequências Inteiras) . Foi criado por Neil Sloan durante sua carreira de pesquisador na AT&T Labs. A OEIS armazena informações sobre seqüências inteiras de interesse para amadores e especialistas em matemática, combinatória, teoria dos números, teoria dos jogos, física, química, biologia, ciência da computação. No momento, 329085 seqüências são coletadas lá. Um registro no OEIS inclui os primeiros elementos de uma sequência, palavras-chave, descrição matemática, sobrenomes dos autores, links para literatura; existe a possibilidade de traçar ou reproduzir uma representação musical da sequência. Uma pesquisa no banco de dados pode ser realizada por palavras-chave e subsequência.

Recentemente, a integração com esse banco de dados apareceu dentro da Wolfram Language (ao usá-lo, é importante entender que este é um desenvolvimento do usuário - recentemente você pode fazer o upload do seu código para o Repositório de Funções Wolfram ). Basta digitar o número da sequência em que você está interessado ou uma lista de números.

 OEISSequenceData = ResourceFunction @ "OEISSequenceData"; OEISSequence = ResourceFunction @ "OEISSequence"; 

ResourceFunction ["OEISSequence"] - simplesmente retorna os primeiros membros da sequência:

 Hold @ OEISSequence @ "A666" 

ResourceFunction ["OEISSequenceData"] - emite um conjunto de dados com informações completas do banco de dados:

 sequenceData[666] = OEISSequenceData[666, "Dataset"] 

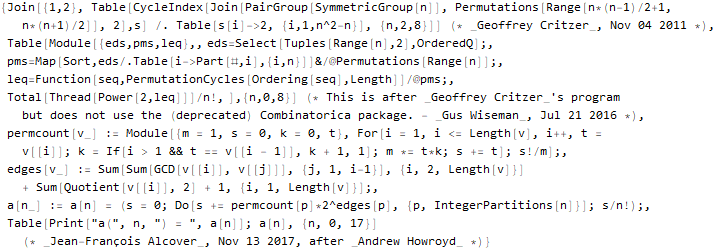
Digamos que você possa "retirar" o código da Wolfram Language:

 Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"] 

Ou um conjunto de sequências selecionadas aleatoriamente com informações de interesse para elas:

 randomSequences = Dataset @ Map[ Normal, OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"] ]; 

 Function[ Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White] ][ Grid[ Join[ { Map[Style[#, Bold, 18]&, {"", "", "", " ", "  "} ] }, Map[ Function[ Map[ Function[ TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"] ], { Style[Part[#, 1], 16], Row[Part[#, 4], "\n"], Row[Part[#, 3], "\n"], Style[Row[Part[#, 2], "; "], 10], ListLinePlot[Part[#, 2], ImageSize -> Full] } ] ], Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}] ] ], Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}}, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], ItemSize -> {{15, 25, 10, 15, 15}, Automatic}, Alignment -> {Left, Center}, Background -> {None, {LightOrange, White}} ] ] 

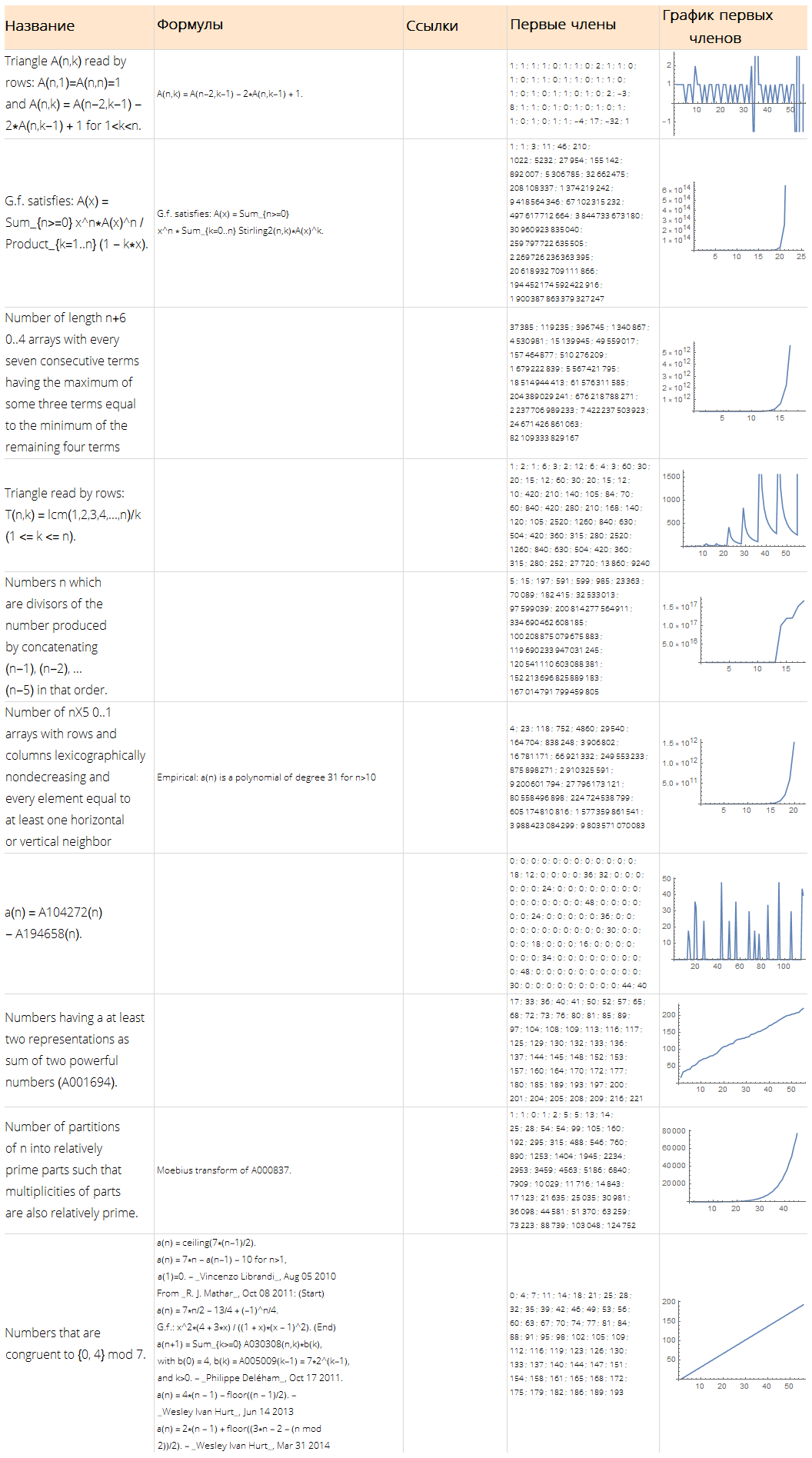
Procure uma fórmula em potencial

Por fim, gostaria de mencionar a função FindFormula , que, com base em um determinado conjunto de números, cria uma fórmula que pode descrevê-los. Podemos aceitar as dependências, você pode escolher muito de diferentes classes de funções.

 data = Table[ { x, Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]] }, {x, RandomReal[{-10, 10}, 1000]} ]; ListPlot[data, Background -> White, ImageSize -> 600] 

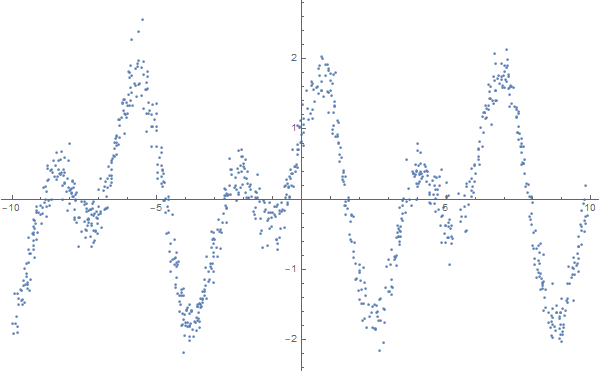
 formulas = FindFormula[data, x] 

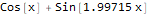
Como você pode ver, a Wolfram Language pegou uma função muito próxima daquela com base na qual dados "ruidosos" foram construídos, a saber - Sin [2x] + Cos [x]:

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], Gray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

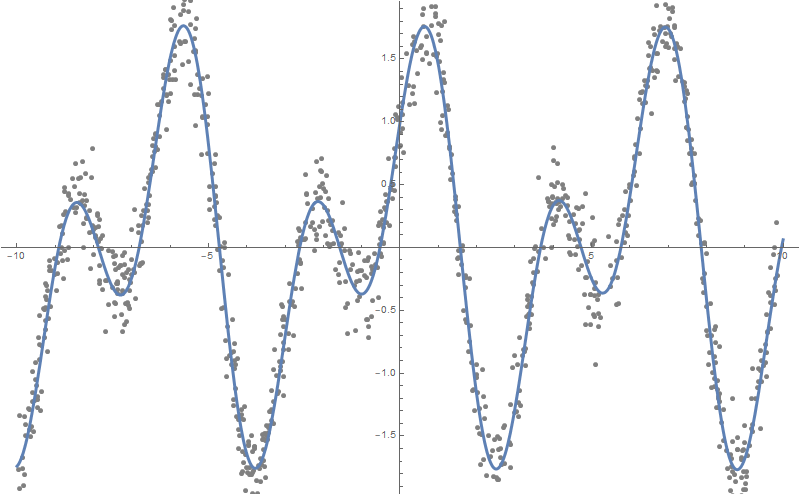
Você pode criar mais dependências, digamos 10:

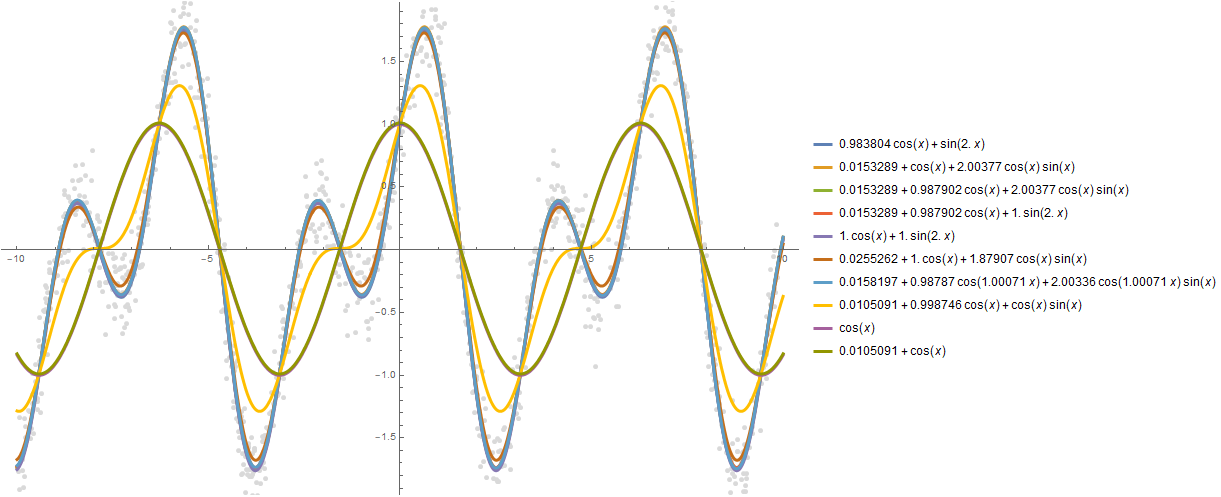
 formulas = FindFormula[data, x, 10] 

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], LightGray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

É importante notar que existe uma função semelhante na funcionalidade que procura uma distribuição de probabilidade - FindDistribution .

Para cooperação - escreva uma mensagem pessoal em Habré ou no meu grupo VKontakte .
Canal do YouTube - seminários on-line e vídeos de treinamento.
Inscrição para novos cursos . Curso online pronto.