👼 ❌ 🙆🏼 Adicione olhos ao robô 😰 ✡️ 👧🏾

Às vezes, um robô precisa pegar alguma coisa. Aquele robô sem olhos, como se sem mãos. No sentido literal. Afinal, sem saber onde está o gostoso, o robô não poderá alcançá-lo com seus braços robóticos. Ou outros manipuladores.

Neste artigo, descobriremos como calibrar o robô para poder alternar entre o Sistema de coordenadas do robô e a câmera 3D.

Etapa 1. Pegue o robô

Teremos itens de movimentação do Dobot Magician. Veja como ele moverá objetos - Intel Realsense D435. E o objeto de calibração terá que ser uma bola vermelha.

É assim que eles parecem juntos.

A bola vermelha é escolhida não apenas para ~~alguém decorar a árvore de Natal~~ . Vermelho - para que possa ser facilmente encontrado na imagem (sem aprender outra rede). Bola - para calcular com mais precisão seu centro na imagem. Mas voltaremos a isso mais tarde.

Etapa 2. Onde o robô move a bola

O algoritmo de calibração pode ser descrito da seguinte maneira:

Gere uma lista de posições no espaço
O robô move a bola pela lista, tirando imagens com ela.
Para cada imagem, encontramos as coordenadas da bola
Calculamos a conversão das coordenadas da câmera em coordenadas do robô

As posições devem ser escolhidas para cobrir o máximo de espaço disponível possível. É melhor não pegar uma bola pequena, pois isso reduzirá a precisão da calibração.

Não forneceremos aqui o código para gravar a calibração, pois ela depende muito do próprio robô, da câmera, do ambiente em que tudo é executado (por exemplo, fizemos em ROS). O importante é que, para uma calibração adicional, você pode tirar fotos mesmo no modo manual, enviando etapas para enviar o robô para as posições e salvando fotos.

O único requisito é que as posições relativas da câmera e do robô permaneçam inalteradas o tempo todo. Também recomendamos que você grave imediatamente o segundo conjunto de imagens para validação - para avaliar com que precisão a calibração foi calculada.

Etapa 3. Obtenha as coordenadas

Conhecemos as coordenadas do manipulador, pois enviamos o robô especialmente para as posições especificadas na lista. Para robôs com um grande número de graus de liberdade, será necessário especificar mais parâmetros, mas em nosso braço de robô de 4 eixos, a posição é determinada exclusivamente pelas coordenadas da ponta do braço do robô. Então, apenas mantemos as posições em que as mãos foram.

Para imagens de bola, suas coordenadas ainda não foram calculadas. Usaremos um objeto bem escolhido para calibração. Reformulamos a tarefa de encontrar uma bola como "encontre a maior região do vermelho", que em python + opencv parecerá:

def get_center(image): #       image = cv2.GaussianBlur(image, (7, 7), 0) #     HSV hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV) #    saturation = hsv[...,1] saturation[(hsv[..., 0] > 15) & (hsv[..., 0] < 165)] = 0 _, image1 = cv2.threshold(saturation, 92, 255, cv2.THRESH_BINARY) #     contours = cv2.findContours(image1, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)[0] contour = max(contours, key=cv2.contourArea) #    b_circle = cv2.minEnclosingCircle(contour) return b_circle[0]

Vamos dar uma olhada.

Depois de converter para o espaço HSV, a imagem fica assim:

Como você pode ver, para pixels escuros, o matiz é bastante barulhento e é necessário um critério adicional para segmentação. Deixe apenas os pixels vermelhos

t e x t h u e [u, v] e m [- 15; 15]

$\ text {hue} [u, v] \ em [-15; 15]$ e observe o canal de saturação. Nesse canal, a bola de calibração se destaca claramente.

Então o critério final ficará assim:

Verifique se a tonalidade está aproximadamente vermelha
Deixe apenas pixels com saturação acima de um determinado limite
Binarizar a imagem

Depois disso, obtemos algo como o seguinte:

Agora você precisa encontrar as coordenadas do centro da esfera. Existem diferentes abordagens, por exemplo, você pode personalizar o modelo 3D da esfera em uma nuvem de pontos. No entanto, para o real Dense D435, os valores de profundidade nas bordas dos objetos são bastante barulhentos, portanto, seguiremos um caminho diferente.

Assumimos que a bola aqui é a maior área conectada. Então encontramos o centro e descobrimos a profundidade até este ponto na superfície da bola, a partir da profundidade do canal. E com uma pequena ajuda da estereometria, vamos passar do ponto visível na superfície da bola para o centro.

Para encontrar o centro da bola, usamos o conhecimento de que a projeção deve ser um círculo e queremos obter uma estimativa imparcial do centro (mas a ventosa do robô está tentando nos impedir). Aqui é suficiente encontrar um círculo da área mínima que descreve essa área, e isso já foi decidido em opencv - minEnclosingCircle .

Tendo recebido as 2 coordenadas do ponto u, v em pixels e a profundidade em milímetros, as traduzimos em coordenadas físicas na câmera SK:

 def get_world_coords(u, v, depth, camera_matrix): f = np.linalg.inv(camera_matrix) l = np.array([u,v,1]) * depth return np.dot(f,l)

camera_matrix - matriz de parâmetros internos da câmera, de acordo com a fórmula .

Etapa 4. Execute a calibração

No momento, recebemos 2 conjuntos de pontos para diferentes posições no espaço: as coordenadas da parte superior da esfera - o ponto em que a bola suga o robô no SC do robô e as coordenadas do centro visível da bola - o ponto da esfera mais próximo da câmera, no SC da câmera. Para compará-los, você primeiro precisa trazê-los para um ponto físico da bola.

E a maneira mais fácil é traduzir esses pontos para o centro da bola. Medimos seu raio r = 24mm. Depois, fica claro como obter as coordenadas do centro da bola O a partir do ponto de tangência K - o toque é sempre 1 raio mais alto ao longo do eixo Z.

Resta traduzir as coordenadas do centro V da região visível nas coordenadas do centro da bola O. Para explicar como fazer isso, use a figura:

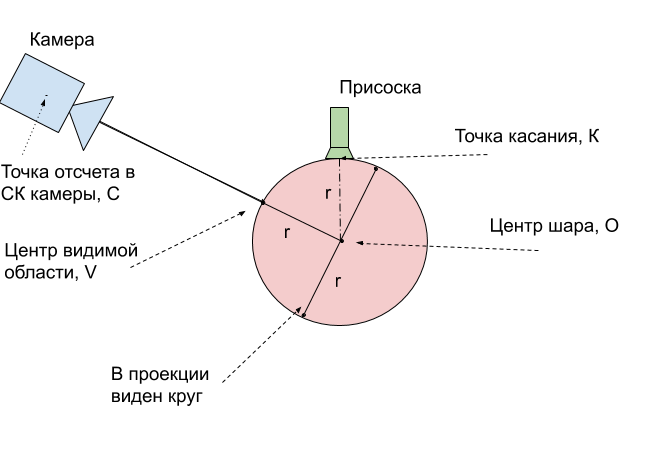
Acontece que o centro real da bola O é sempre exatamente 1 raio mais profundo que o ponto visível V. Isso significa que o vetor do raio encontrado deve ser estendido em 24 mm.

v e c C O = v e c C V + f r a c v e c C V | v e c C V | r

$\ vec {CO} = \ vec {CV} + \ frac {\ vec {CV}} {| \ vec {CV} |} r$

Permanece um pouco - tendo 2 conjuntos de coordenadas 3D correspondentes aos mesmos pontos físicos, encontre a transformação do primeiro conjunto no segundo. Usaremos a função opencv cv2.estimateAffine3D para isso. Para coordenadas encontradas idealmente, a transformação afim é, obviamente, a enumeração; para descrever a transformação de pontos, rotação e deslocamento são suficientes, o alongamento será supérfluo. No entanto, o uso de transformação afim permite compensar imprecisões com uma matriz mal calculada de parâmetros internos da câmera. Mais do que isso, permite obter uma calibração sem conhecê-las.

 transformation = cv2.estimateAffine3D(camera_coords, robot_coords)

A saída é uma matriz de transformação 3x4, os primeiros componentes 3x3 são uma matriz de rotação combinada com extensão ao longo dos eixos. Com a calibração correta da câmera e bons dados de entrada, você deve obter uma matriz próxima à matriz de rotação. Os três números restantes são o vetor de deslocamento entre a câmera e o robô.

Etapa 5. Usamos calibração

Para usar a calibração obtida, é necessário repetir as transformações indicadas. Nós os trazemos para um único algoritmo.

Encontramos na imagem RGBD as coordenadas do ponto u, v, profundidade de interesse para nós
Nós as traduzimos em coordenadas físicas x, y, z na câmera SK usando a matriz de parâmetros internos
No caso de uma bola, o ponto de interesse para nós é a profundidade da bola $v '= \ frac {| v | + r} {| v |} \ cdot v, v = [x, y, z]$
Aplicamos a transformação de transformação encontrada, que denotamos pela matriz T
$v '' = T \ times [v'_0, v'_1, v'_2, 1] ^ T$
Temos as coordenadas do centro da bola no robô SK. Para que o robô não tente furar a bola, enviamos um raio de ponto 1 maior para controle $v '' '= [v' '_ 0, v' '_ 1, v' '_ 2 + r]$

Precisão da calibração

Calculamos a calibração em 9 posições. Em um conjunto de validação de mais 6 posições, foi obtida uma precisão de 2,5 mm com uma área de trabalho de 16x30x5 cm. Para isso, aplicamos a transformação encontrada nas imagens restantes e calculamos o comprimento médio do vetor de erro.

Etapa 6. Usamos nas tarefas aplicadas

Após a calibração, você pode começar a resolver problemas reais. Por exemplo, conectamos um capacete de realidade virtual aos controladores e conseguimos controlar o robô e mover os cubos em realidade virtual.

Mas esse método de calibração é bastante geral. Não importa qual câmera e robô são usados, o método descrito facilita o cálculo da relação entre os sistemas de coordenadas do robô e da câmera. Além disso, com pequenas alterações, o método é autônomo, para que o robô possa executar a calibração automaticamente, pois com o tempo a câmera se moverá em relação ao robô.

Vasyutka e ZlodeiBaal e eu planejamos continuar falando sobre o mundo dos robôs, VR e aprendizado de máquina, se for interessante. E fontes de calibração podem ser encontradas no meu local .

Adicione olhos ao robô

More articles: