“Protocolos de sistemas de criptografia”: Diffie - Hellman, El-Gamal, MTI / A (0), STS

Como os criadores dos protocolos de três passagens da seção anterior , os autores dos algoritmos a seguir os consideraram não apenas construções matemáticas, fornecendo alguma operação elementar (por exemplo, criptografia de chave pública), mas tentaram construir um sistema completo de distribuição de chaves em torno de uma ou duas fórmulas. Algumas dessas construções, que foram transformadas, são usadas até o momento (por exemplo, o protocolo Diffie-Hellman), algumas delas permanecem apenas no histórico de criptografia e proteção de informações.

Mais tarde, na década de 1990, primitivos matemáticos assimétricos (criptografia e assinatura eletrônica) e protocolos serão separados, esses primitivos serão utilizados, o que será demonstrado na seção sobre protocolos assimétricos.

Protocolo Diffie - Hellman

O primeiro algoritmo de chave pública foi proposto por Diffie e Hellman em 1976, "Novas direções em criptografia" ( Bailey Whitfield Diffie, Martin Edward Hellman, "Novas direções em criptografia" , [Diffie, Hellman 1976] ). Esse protocolo, que também pode ser chamado de esquema Diffie-Hellman , foi o primeiro a reduzir os requisitos para o canal de comunicação estabelecer uma conexão segura sem primeiro trocar chaves.

O protocolo permite que duas partes criem uma chave de sessão comum usando um canal de comunicação que um invasor possa ouvir, mas supondo que esse último não possa alterar o conteúdo das mensagens.

Vamos $$$p$ - um grande número primo $$$g$ - um elemento primitivo do grupo $$$\ mathbb {Z} _p ^ *$ , $$$y = g ^ x \ bmod p$ e $$$p$ , $$$y$ e $$$g$ previamente conhecido. Função $$$y = g ^ {x} \ bmod p$ consideramos unidirecional, ou seja, calcular uma função com um valor conhecido de um argumento é uma tarefa fácil, e sua inversão (encontrar um argumento) com um valor conhecido de uma função é difícil. (Função inversa $$$x = \ log_g y \ bmod p$ chamada de função de logaritmo discreto. Atualmente, não há maneiras rápidas de calcular essa função para grandes e simples $$$p$ .)

O protocolo de troca consiste nas seguintes ações.

1. Alice escolhe um aleatório $$$2 \ leq a \ leq p - 1$
   $$$Alice \ à \ esquerda \ {A = g ^ a \ bmod p \ right \} \ para Bob$
2. Bob escolhe aleatoriamente $$$2 \ leq b \ leq p-1$
   Bob calcula a chave da sessão $$$K = A ^ b \ bmod p$
   $$$Bob \ à \ esquerda \ {B = g ^ b \ bmod p \ direita \} \ para Alice$
3. Alice calcula $$$K = B ^ a \ bmod p$
   

Dessa maneira, uma chave de sessão secreta compartilhada é criada $$$K$ . Devido à seleção aleatória de valores $$$a$ e $$$b$ em uma nova sessão, uma nova chave de sessão será recebida.

O protocolo fornece apenas a geração de novas chaves de sessão (destino G10). Na ausência de uma terceira parte confiável, ela não fornece autenticação das partes (objetivo G1), devido à falta de passagens com confirmação da propriedade da chave, não há autenticação de chave (objetivo G8). Porém, como o protocolo não usa chaves “mestras” longas, podemos dizer que possui a propriedade de perfeito sigilo direto (objetivo G9).

O protocolo pode ser usado apenas com canais de comunicação nos quais um criptoanalista ativo não pode intervir. Caso contrário, o protocolo se torna vulnerável a um simples "ataque do meio".

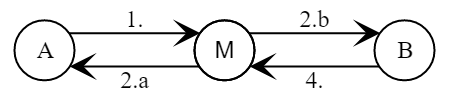
1. Alice escolhe um aleatório $$$2 \ leq a \ leq p - 1$
   $$$Alice \ à \ esquerda \ {A = g ^ a \ bmod p \ direita \} \ para Mellory ~ (Bob)$
2. Mallory escolhe um aleatório $$$2 \ leq m \ leq p-1$
   Mallory calcula uma chave de sessão para um canal com Alice
   

   $$

   $$K_ {AM} = A ^ m \ bmod p = g ^ {am} \ bmod p$$
   
   $$$Mellory ~ (Alice) \ para \ esquerda \ {M = g ^ m \ bmod p \ right \} \ para Bob$
   $$$Mellory ~ (Bob) \ para \ esquerda \ {M = g ^ m \ bmod p \ right \} \ para Alice$
3. Alice calcula a chave da sessão do canal com Mallory (pensando que Mallory é Bob)
   

   $$

   $$K_ {AM} = M ^ a \ bmod p = g ^ {am} \ bmod p$$
4. Bob escolhe aleatoriamente $$$2 \ leq b \ leq p-1$
   Bob calcula a chave da sessão do canal com Mallory (pensando que Mallory é Alice)
   

   $$

   $$K_ {BM} = M ^ b \ bmod p = g ^ {bm} \ bmod p$$
   
   $$$Bob \ à \ esquerda \ {B = g ^ b \ bmod p \ direita \} \ para Mellory ~ (Alice)$
5. Mallory calcula uma chave de sessão para um canal com Bob
   

   $$

   $$K_ {BM} = B ^ m \ bmod p = g ^ {bm} \ bmod p$$
   
   

Como resultado, Alice e Bob receberam novas chaves de sessão, mas não estabeleceram um canal de comunicação "seguro" entre si, mas com um invasor que agora tem a capacidade de retransmitir ou alterar todas as mensagens transmitidas entre Alice e Bob.

O protocolo Diffie-Hellman difere da maioria dos protocolos de distribuição de chaves devido ao fato de não usar outras primitivas criptográficas (criptografia, assinatura digital ou funções de hash), mas por si só é, em certo sentido, uma primitiva criptográfica para a construção de protocolos mais complexos. Ele fornece geração aleatória de números em um sistema distribuído sem um centro confiável. Além disso, nenhum dos lados pode forçar o outro a usar a chave de sessão antiga, ao contrário, por exemplo, do protocolo Yahalom.

O protocolo pode ser alterado para que, em vez do grupo multiplicativo de multiplicação simples, use o grupo aditivo de adição de pontos da curva elíptica. Nesse caso, as partes ainda escolherão alguns números inteiros aleatórios, mas não aumentam o número do gerador para uma potência, mas multiplicam o ponto do gerador pelo número desejado.

1. As partes concordaram com um grupo de pontos da curva elíptica $$$\ mathbb {E}$ seu subgrupo cíclico $$$\ mathbb {G}$ poder $$$n = \ | \ mathbb {G} \ |$ e gerador $$$G$ grupos $$$\ mathbb {G}$ (ou pelo menos um subgrupo suficientemente grande do grupo $$$\ mathbb {G}$ )
2. Alice escolhe um aleatório $$
   $$$Alice \ à \ esquerda \ {A = a \ vezes G \ direita \} \ para Bob$
3. Bob escolhe aleatoriamente $$$2 \ leq b \ leq n - 1$
   Bob calcula o ponto $$$K = b \ vezes A$
   $$$Bob \ à \ esquerda \ {B = g \ vezes G \ direita \} \ para Alice$
4. Alice calcula o ponto $$$K = a \ vezes B$

Como uma nova chave de sessão, as partes podem escolher, por exemplo, a primeira coordenada do ponto encontrado $$$K$ .

Protocolo El Gamal

O protocolo El-Gamal ( [ElGamal, 1984] , [ElGamal, 1985] ), devido à distribuição preliminar da chave pública de uma das partes, fornece autenticação da chave para esse lado. Pode-se garantir que apenas o proprietário da chave privada correspondente possa calcular a chave da sessão. No entanto, a confirmação do recebimento da chave (cumprimento das metas G1 e G8) não faz parte do protocolo.

1. Alice e Bob escolhem opções comuns $$$p$ e $$$g$ onde $$$p$ É um grande número primo e $$$g$ - elemento de campo primitivo $$$\ mathbb {Z} _p ^ *$ .
   Bob cria um par de chaves públicas e privadas $$$b$ e $$$K_B$ :
   

   $$

   $$\ begin {array} {l} b: 2 \ leq b \ leq p - 1, \\ K_B = g ^ b \ bmod p. \ end {array}$$
   
   Chave pública $$$K_B$ É de acesso público e aberto a todas as partes. Um criptoanalista não pode substituí-lo - a substituição será perceptível.
2. Alice escolhe um segredo $$$x$ e calcula a chave da sessão $$$K$
   

   $$

   $$K = K_B ^ {x} = g ^ {bx} \ bmod p.$$
   
   

   $$

   $$Alice \ à \ esquerda \ {g ^ x \ bmod p \ right \} \ para Bob$$
3. Bob calcula a chave da sessão
   

   $$

   $$K = (g ^ x) ^ {b} = g ^ {bx} \ bmod p.$$

O protocolo não garante a seleção de uma nova chave de sessão em cada sessão de protocolo (G10) e o uso de uma chave "principal" $$$K_B$ transferir uma chave de sessão permite que um invasor calcule todas as chaves de sessão de sessões anteriores quando uma chave privada é comprometida $$$b$ (objetivo G9).

Protocolo MTI / A (0)

Em 1986, C. Matsumoto ( Tsutomu Matsumoto ), I. Takashima ( Youichi Takashima ) e H. Imai ( Hideki Imai ) propuseram vários algoritmos, posteriormente denominados família de protocolo MTI ( [Matsumoto, Tsutomu, Imai 1986] ). Devido à distribuição preliminar das chaves públicas de ambas as partes, eles forneceram autenticação implícita de chave (destino G7). Ou seja, só é possível garantir que uma chave de sessão seja recebida pelos proprietários das chaves públicas correspondentes. Vamos considerar um dos representantes dessa família - o protocolo MTI / A (0).

Anteriormente, as partes concordavam com os parâmetros gerais do sistema. $$$p$ e $$$g$ onde $$$p$ É um grande número primo e $$$g$ - elemento de campo primitivo $$$\ mathbb {Z} _p ^ *$ .


Cada uma das partes (Alice e Bob) gerou um par de chaves públicas e privadas:

$$

$$\ begin {array} {ll} Alice: & ~ a, ~~ K_A = g ^ a \ bmod p, \\ Bob: & ~ b, ~~ K_B = g ^ b \ bmod p. \\ \ end {array}$$

1. Alice gerou um número aleatório $$$R_A: ~ 2 \ leq R_A \ leq p-1$
   $$$Alice \ à \ esquerda \ {g ^ {R_A} \ bmod p \ direita \} \ para Bob$
2. Bob gerou um número aleatório $$$R_B: ~ 2 \ leq R_B \ leq p-1$
   Bob descobriu uma chave de sessão $$$K = (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p$
   $$$Bob \ à \ esquerda \ {g ^ {R_B} \ bmod p \ direita \} \ para Alice$
3. Alice calculou a chave da sessão $$$K = (g ^ {R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p$

Se as chaves públicas $$$K_A$ e $$$K_B$ combine suas chaves privadas $$$a$ e $$$b$ , as chaves da sessão calculadas pelos participantes correspondem:

$$

$$\ begin {array} {lll} (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p & = & g ^ {b R_A + a R_B} \ bmod p, \\ (g ^ { R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p & = & g ^ {a R_B + b R_A} \ bmod p. \ end {array}$$

Devido à complexidade da tarefa discreta de logaritmo, um invasor não poderá obter $$$a, R_A$ ou $$$b, R_B$ das mensagens transmitidas e a publicação preliminar de chaves públicas garante que apenas usuários legítimos recebam a chave da sessão. Seleção aleatória $$$R_A$ e $$$R_B$ garante que ambas as partes possam ter certeza de criar uma nova chave de sessão em cada sessão de protocolo.

Como outros representantes dos protocolos do sistema de criptografia, o MTI não foi desenvolvido levando em consideração a possibilidade de comprometer chaves "mestras" fechadas $$$a$ e $$$b$ (objetivo G9).

Protocolo Estação a Estação

O protocolo STS ( estação a estação , [Diffie, Oorschot, Wiener 1992] ) é destinado a sistemas de comunicação móvel. Ele usa as idéias do protocolo Diffie-Hellman e do sistema de criptografia RSA. Uma característica do protocolo é o uso de um mecanismo de assinatura eletrônica para autenticação mútua das partes.

Anteriormente, as partes concordavam com os parâmetros gerais do sistema. $$$p$ e $$$g$ onde $$$p$ É um grande número primo e $$$g$ - elemento de campo primitivo $$$\ mathbb {Z} _p ^ *$ .

Cada lado $$$A$ e $$$B$ possui um par de chaves de longo prazo: uma chave privada para descriptografar e criar uma assinatura eletrônica $$$K _ {\ text {public}}$ e chave pública para verificação de criptografia e assinatura $$$K _ {\ text {public}}$ .

$$

$$\ begin {array} {ll} A: K_ {A, \ text {private}}, K_ {A, \ text {public}}: \ forall M: & \ text {Verificar} _A (M, S_A (M )) = true, \\ & D_A (E_A (M)) = M, \\ B: K_ {B, \ text {private}}, K_ {B, \ text {public}}: \ forall M: & \ texto {Verificar} _B (M, S_B (M)) = verdadeiro, \\ & D_B (E_B (M)) = M. \\ \ end {array}$$

Onde $$$\ text {Verificar} _A (\ pontos)$ é uma função de verificar assinatura eletrônica em uma chave pública $$$K_ {A, \ text {public}}$ e $$$D_A$ - função de descriptografia usando a chave privada $$$K_ {A, \ text {private}}$ .

O protocolo consiste em quatro passagens, três das quais incluem a transmissão de mensagens ( [Cheryomushkin 2009] ).

1. Alice escolhe um número aleatório $$$R_A: 2 \ leq R_A \ leq p-1$ .
   $$$Alice \ à \ esquerda \ {A, m_A = g ^ {R_A} \ bmod p \ direita \} \ para Bob$
2. Bob escolhe um número aleatório $$$R_B: 2 \ leq R_B \ leq p-1$ .
   Bob calcula a chave da sessão $$$K = m_A ^ {R_B} \ bmod p$ .
   $$$Bob \ à \ esquerda \ {B, A, m_B = g ^ {R_B} \ bmod p, E_K (S_B (m_A, m_B)) \ right \} \ para Alice$
3. Alice calcula uma chave de sessão $$$K = m_B ^ {R_A} \ bmod p$ .
   Alice verifica a assinatura na mensagem $$$E_K (S_B (m_A, m_B))$ .
   $$$Alice \ à \ esquerda \ {A, B, E_K (S_A (m_A, m_B)) \ direita \} \ para Bob$
4. Bob verifica a assinatura na mensagem $$$E_K (S_A (m_A, m_B))$ .

O protocolo garante a garantia da formação de novas chaves (G10), mas não o perfeito sigilo direto (G9).

Como o ataque Lowe de 1996 ( [Lowe 1996] ) mostrou, um protocolo não pode garantir a autenticação de sujeitos (alvo G1), chaves (G7) e prova de propriedade da chave da sessão (G8). Embora o invasor não possa obter acesso à nova chave de sessão se o protocolo for usado apenas para autenticar os participantes, Alice pode confundir o invasor com Bob.

1. Alice escolhe um número aleatório $$$R_A: 2 \ leq R_A \ leq p-1$ .
   $$$Alice \ à \ esquerda \ {A, m_A = g ^ {R_A} \ bmod p \ direita \} \ para Mellory ~ (Bob)$
   
2. $$$Mellory \ à \ esquerda \ {M, m_A \ right \} \ para Bob$
   
3. Bob escolhe um número aleatório $$$R_B: 2 \ leq R_B \ leq p-1$ .
   Bob calcula a chave da sessão $$$K = m_A ^ {R_B} \ bmod p$ .
   $$$Bob \ à \ esquerda \ {B, M, m_B, E_K (S_B (m_A, m_B)) \ direita \} \ em Mellory$
   
4. $$$Mellory ~ (Bob) \ para \ esquerda \ {B, A, E_K (S_B (m_A, m_B)) \ right \} \ para Alice$
   
5. Alice calcula uma chave de sessão $$$K = m_B ^ {R_A} \ bmod p$ .
   Alice verifica a assinatura na mensagem $$$E_K (S_B (m_A, m_B))$ .
   $$$Alice \ à \ esquerda \ {A, B, E_K (S_A (m_A, m_B)) \ direita \} \ para Mellory ~ (Bob)$
   

Depois de concluir com sucesso o protocolo, Alice está confiante de que está se comunicando com Bob.

Como todos os outros “protocolos de sistema de criptografia”, o protocolo Estação a Estação é baseado em alguma fonte externa de informações sobre as chaves públicas dos participantes, sem questionar a correção e a confiabilidade dessa fonte. O que, no caso geral, está incorreto. Se as informações sobre as chaves dos participantes precisarem ser recebidas externamente em cada sessão do protocolo (por exemplo, se houver muitos participantes e não houver a possibilidade de lembrar as chaves de todos), o canal para obter chaves públicas será o principal objetivo de um criptoanalista ativo para os protocolos considerados. Como se proteger disso usando primitivas de criptografia assimétrica está na próxima seção.

Literatura

• [Diffie, Hellman 1976] Diffie W., Hellman ME Novas direções em criptografia // Teoria da Informação, Transações IEEE em. - 1976. - novembro - t. 22, n º 6. - p. 644-654. - ISSN 0018-9448. - DOI: 10.1109 / TIT.1976.1055638.
• [ElGamal, 1984] El Gamal T. Um sistema de criptografia de chave pública e um esquema de assinatura baseado em logaritmos discretos // Anais do CRYPTO 84 sobre avanços em criptografia. - Santa Barbara, Califórnia, EUA: Springer-Verlag New York, Inc., 1985 - p. 10-18. - ISBN 0-387-15658-5. - URL: dl.acm.org/citation.cfm?id=19478.19480 .
• [ElGamal, 1985] El Gamal T. Um sistema de criptografia de chave pública e um esquema de assinatura baseado em logaritmos discretos // IEEE Transactions on Information Theory. - 1985. - julho. - t 31, n º 4. - p. 469-472. - DOI: 10.1109 / TIT.1985.1057074.
• [Matsumoto, Tsutomu, Imai 1986] Matsumoto T., Takashima Y., Imai H. Em busca de sistemas inteligentes de distribuição de chaves públicas // Trans. Inst. Elétron Commun. Eng. Jpn. Seita. E. T. 69. edição 2. - 02.1986. - com 99-106.
• [Diffie, Oorschot, Wiener 1992] Diffie W., PC de Van Oorschot, Wiener MJ Authentication
  e trocas de chaves autenticadas // Designs, códigos e criptografia. - 1992. - junho. - t. 2, n. 2. - p. 107-125. - ISSN 1573-7586. - DOI: 10.1007 / BF00124891.
• [Lowe 1996] Lowe G. Alguns novos ataques a protocolos de segurança // CSFW '96 Anais do 9º workshop do IEEE sobre Fundamentos de Segurança em Computadores. - Washington, DC, EUA: IEEE Computer Society, 1996. - p. 162
• [Cheremushkin 2009] Cheremushkin A. V. Protocolos criptográficos: propriedades básicas e vulnerabilidades // Matemática Discreta Aplicada. - 2009. - novembro - questão. 2. - p. 115-150. - URL: cyberleninka.ru/article/n/kriptograficheskieprotokoly-osnovnye-svoystva-i-uyazvimosti.pdf .