Duas obras monumentais convenceram muitos matemáticos a abandonar o sinal de igual. Seu objetivo é reconstruir os fundamentos da disciplina com a ajuda de um relacionamento mais fraco - "equivalência". E esse processo nem sempre ocorre sem problemas.
O sinal de igual é a pedra angular da matemática. Ele parece fazer uma afirmação fundamental e consistente: essas duas entidades são exatamente iguais.
No entanto, o círculo de matemáticos está crescendo, referindo-se ao sinal de igual, assim como ao erro inicial da matemática. Eles consideram isso um brilho externo, ocultando as importantes dificuldades da relação de quantidades - dificuldades que podem abrir soluções para um grande número de problemas. Eles querem reformar a matemática usando uma linguagem de equivalência mais flexível.
"Geramos essa idéia de igualdade", disse
Jonathan Campbell, da Universidade Duke. "E deveria ter havido equivalência em seu lugar."
A figura mais proeminente nessa comunidade é
Jacob Lurie . Em julho,
Lurie , de 41 anos, renunciou como funcionário em tempo integral em Harvard para um cargo de professor no Instituto de Estudos Avançados de Princeton, onde trabalhavam alguns dos principais matemáticos do mundo.
Ideias de uma escala como a de Lurie raramente são encontradas em qualquer campo. Em seus livros, abrangendo milhares de páginas cheias de detalhes técnicos, ele criou uma maneira surpreendentemente diferente da maneira usual de entender os conceitos mais básicos da matemática, indo além do sinal de igual. "Acho que lhe parecia que esse era o jeito certo de pensar em matemática", disse
Michael Hopkins , matemático de Harvard e diretor da escola de pós-graduação.
Ele publicou seu primeiro livro, The
Theory of Higher Topos , em 2009. Um volume de 944 páginas serve como uma instrução para interpretar áreas reconhecidas da matemática no novo idioma das "categorias do infinito". Nos anos seguintes, as idéias de Lurie penetraram em uma ampla gama de disciplinas matemáticas. Muitos matemáticos os consideram indispensáveis para o futuro deste campo. "Ninguém será o mesmo depois de estudar as categorias do infinito", disse
John Francis da Northwestern University,
Jacob LurieNo entanto, a disseminação das categorias do infinito revelou todos os problemas pelos quais passa um campo respeitado da matemática, tentando absorver novas idéias ousadas - especialmente uma que desafia seu conceito mais importante. "Existe um certo nível de conservadorismo na comunidade matemática", disse
Clark Barwick, da Universidade de Edimburgo. "Não acho que se espere que qualquer grupo de matemáticos aceite rapidamente qualquer ferramenta sem razões convincentes".
Embora muitos matemáticos tenham aceitado as categorias do infinito, poucos leram os textos inteiros e extremamente abstratos de Lurie. Como resultado, parte do trabalho baseado em suas idéias acaba sendo menos rigorosa do que é aceito em matemática.
"Ouvi as pessoas dizerem: 'Lurie tem em algum lugar'", disse
Inna Zakharevich , matemática da Universidade de Cornell. - E eu digo: 'Sério? Você se refere a 8.000 páginas de texto. Isso não é uma referência, é um apelo à autoridade. ”
Os matemáticos ainda estão tentando perceber a amplitude das idéias de Lurie e a maneira única de apresentá-las. Eles extraem a essência de sua apresentação das categorias do infinito e a apresentam em um novo pacote para que mais matemáticos possam usá-lo. Em certo sentido, eles exercem a liderança necessária, que é obrigada a seguir qualquer revolução, traduzindo o texto revolucionário no código de leis cotidiano. Assim, eles criam o futuro dos matemáticos, baseados não na igualdade, mas na equivalência.
Torres de equivalência sem fim
A igualdade matemática parece a menos controversa de todas as idéias. Duas contas mais uma conta é igual a três contas. Sobre o que mais podemos falar? No entanto, as idéias mais simples podem ser as mais enganosas.
Desde o final do século 19, os fundamentos da matemática foram construídos sobre conjuntos de objetos chamados conjuntos. A teoria dos conjuntos define as regras, ou axioma, para a criação e manipulação desses conjuntos. Um desses axiomas, por exemplo, afirma que você pode adicionar um conjunto de um elemento a um conjunto de dois elementos e obter um novo conjunto de três elementos: 2 + 1 = 3.
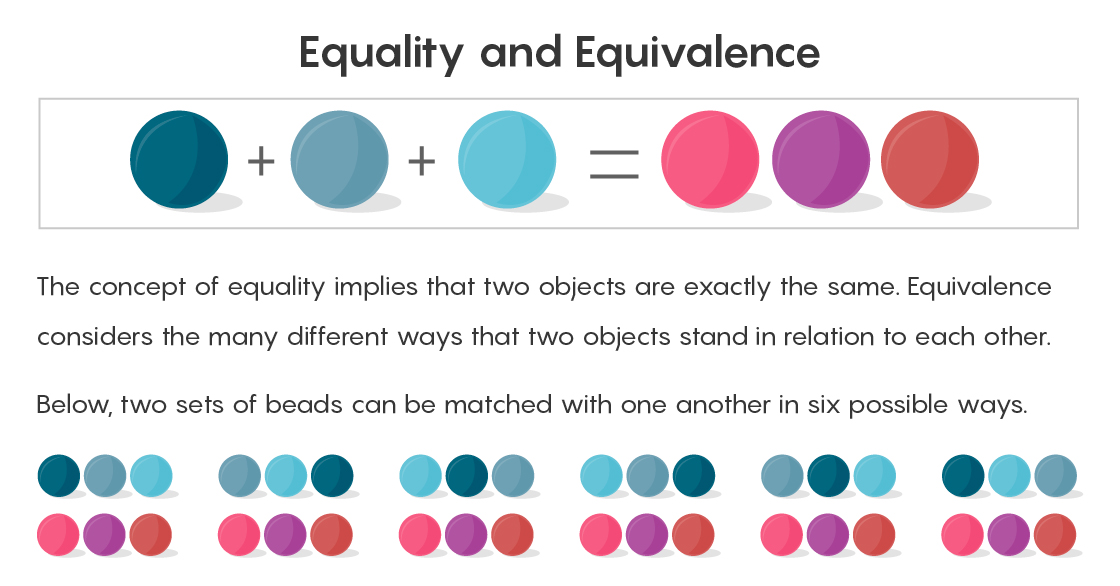
A maneira formal de demonstrar a igualdade de duas quantidades é combinar pares entre si. Combine uma conta à direita do sinal de igual com uma conta à esquerda. Depois de todas as comparações, não haverá contas extras.
A teoria dos conjuntos reconhece que dois conjuntos de três objetos cada um podem ser correspondidos com precisão, mas não significa todas as diferentes formas possíveis de tal comparação. O primeiro cordão à direita pode pegar um par na forma do primeiro cordão à esquerda, ou igualar o primeiro à direita com o segundo à esquerda, e assim por diante (pode haver seis desses pares). Dizer que dois mais um é igual a três, e termina com isso significa não ver todas as maneiras possíveis para igualá-las. "O problema é que existem muitas maneiras de emparelhar", diz Campbell. "E nós os esquecemos quando dizemos iguais."
É aqui que a equivalência entra em jogo. Se a igualdade é uma relação clara - duas coisas são iguais ou não - a equivalência pode ser diferente.
Quando você combina com precisão cada elemento de um conjunto com cada elemento de outro, obtém forte equivalência. Mas, por exemplo, em um campo da matemática como a
homotopia , duas formas (ou figuras geométricas) são equivalentes se uma pode ser transformada em outra esticando ou comprimindo sem quebrar.
Do ponto de vista da teoria da homotopia, um disco plano e um ponto no espaço são equivalentes - o disco pode ser comprimido em um ponto. No entanto, você não pode combinar os pontos em um disco com os pontos em um ponto. De fato, o disco de pontos tem um número infinito, e um ponto é apenas um ponto.
Desde meados do século XX, os matemáticos tentam desenvolver uma alternativa para definir a teoria na qual a matemática seria mais fácil de lidar em termos de equivalência. Em 1945, os matemáticos
Samuel Eileberg e
Saunders MacLane introduziram um novo objeto fundamental com equivalência embutida. Eles chamavam de categoria.
Uma categoria pode ser preenchida com qualquer coisa. Você pode escolher a categoria de mamíferos, que incluirá todas as criaturas peludas de sangue quente que produzem leite. Ou você pode criar categorias de objetos matemáticos: conjuntos, formas geométricas ou sistemas numéricos.
Uma categoria é um conjunto com metadados adicionais: uma descrição de todas as maneiras de corresponder um objeto a outro, que inclui uma descrição de todos os recursos pelos quais dois objetos podem ser considerados equivalentes. As categorias também podem ser imaginadas como objetos geométricos nos quais cada elemento da categoria é representado por um ponto.
Imagine, por exemplo, a superfície de uma bola. Cada ponto nesta superfície pode indicar seu tipo de triângulos. Caminhos entre pontos expressam uma relação de equivalência entre objetos. Do ponto de vista da teoria das categorias, esquecemos a maneira específica de descrever um objeto e, em vez disso, nos concentramos em qual lugar o objeto ocupa em relação a todos os outros objetos desse tipo.
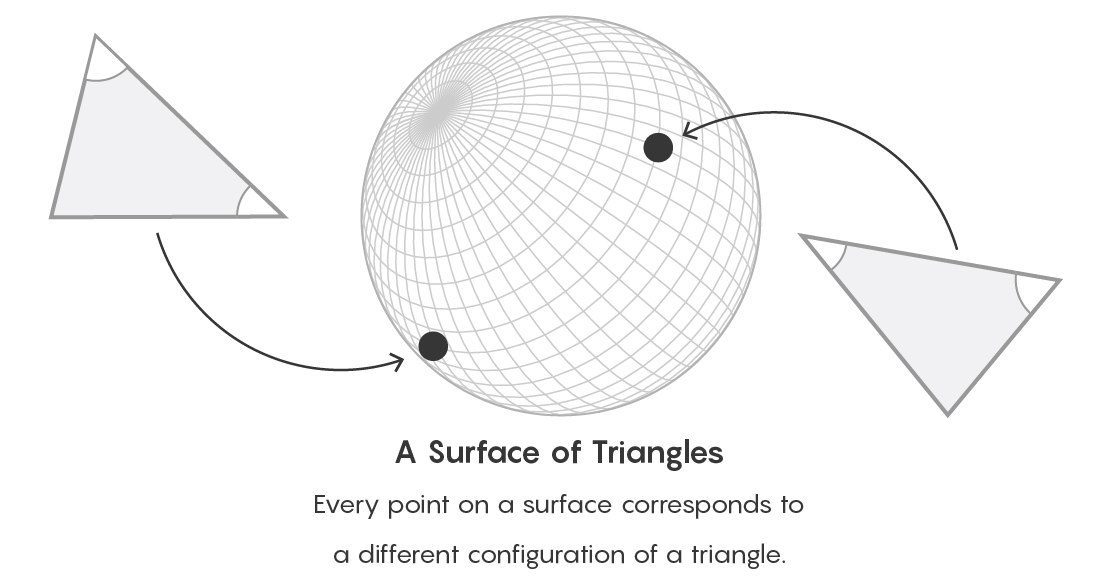Cada ponto na superfície corresponde a um tipo particular de triângulos."Tratamos muitas coisas como coisas, embora na realidade elas sejam um relacionamento entre as coisas", disse Zakharevich. - A frase "meu marido" significa algo que consideramos um objeto, mas você pode pensar nisso como um relacionamento. Uma certa parte disso é determinada pelo relacionamento comigo.
A versão da categoria de Eilenberg e MacLane era adequada para trabalhar com fortes opções de equivalência. Mas na segunda metade do século XX, os matemáticos usavam cada vez mais formas mais fracas de equivalência, como a homotopia. "A matemática está se tornando mais sutil e, inevitavelmente, desejamos idéias mais sutis sobre coisas comuns", disse Emily Riel, matemática da Johns Hopkins University. Nessas versões mais refinadas da equivalência, a quantidade de informações sobre o relacionamento entre dois objetos aumenta acentuadamente. As categorias rudimentares de Eilenberg e MacLane não foram feitas para isso.
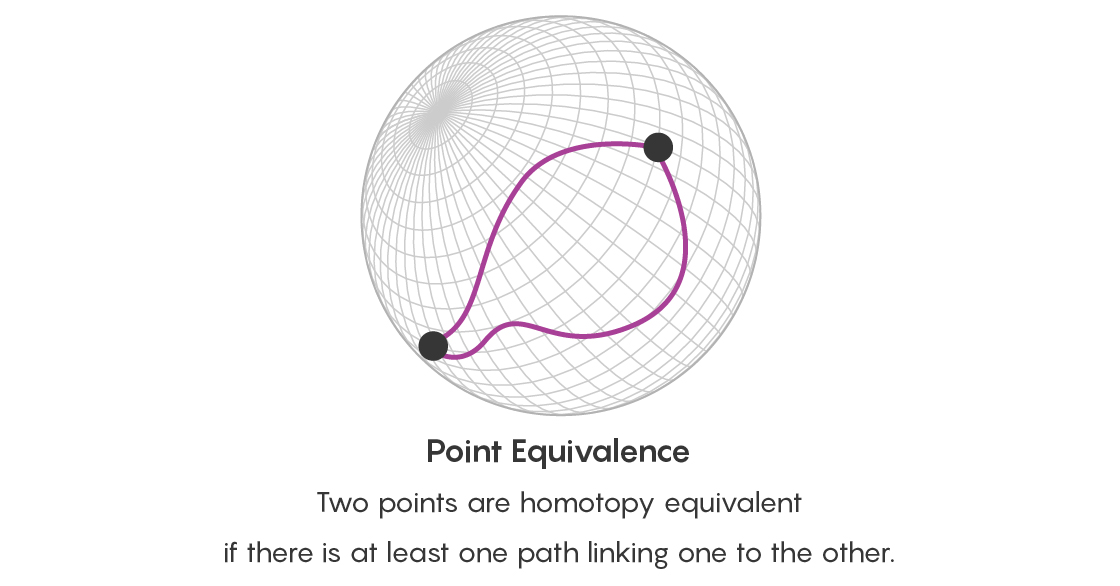
Para ver um aumento na quantidade de informações, lembre-se primeiro da nossa esfera, denotando diferentes triângulos. Dois triângulos são homotopicamente equivalentes se um puder ser transformado em outro por alongamento ou outra deformação. Dois pontos em uma superfície são homotopicamente equivalentes se houver um caminho que os conecte. Ao estudar caminhos homotópicos entre pontos em uma superfície, você está realmente estudando as diferentes maneiras pelas quais os triângulos indicados por esses pontos são conectados entre si.
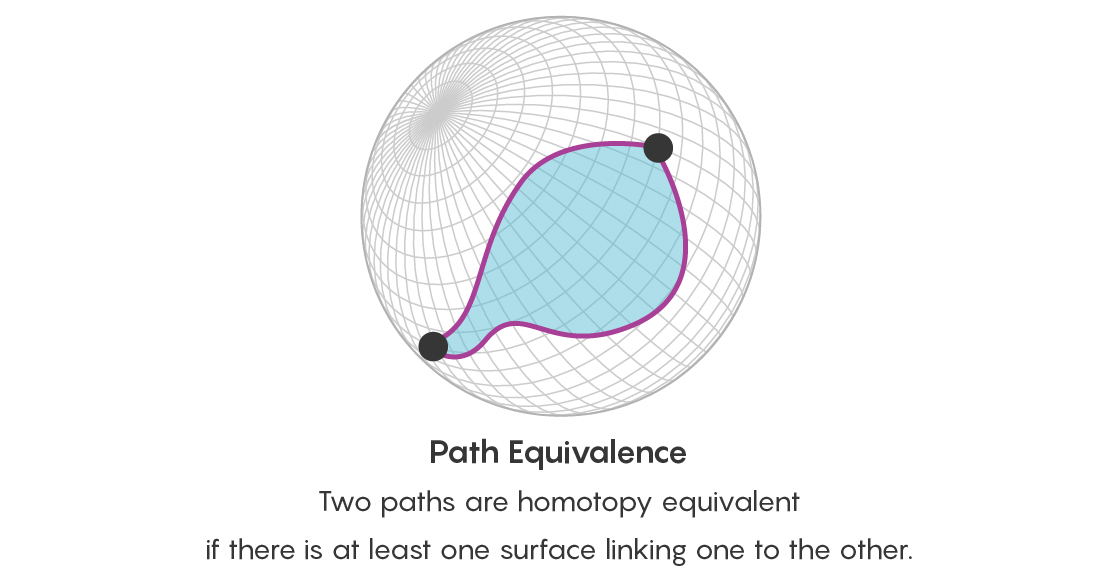
No entanto, não basta afirmar que dois pontos estão conectados de muitas maneiras equivalentes. Também é necessário pensar na equivalência de todos esses caminhos. Portanto, além da questão da equivalência de pontos, agora você faz a pergunta da equivalência de dois caminhos que começam e terminam nos mesmos pontos - e existe um caminho que liga esses caminhos. Esse caminho que conecta os caminhos assume a forma de um disco, cujo limite são dois desses caminhos.
Você pode desenvolver essa idéia ainda mais. Dois discos são equivalentes se estiverem conectados por um caminho - e esse caminho assumirá a forma de um objeto tridimensional. Esses objetos tridimensionais podem ser conectados por caminhos quadridimensionais (o caminho entre dois objetos sempre tem uma dimensão a mais que os próprios objetos).
Como resultado, você constrói uma torre interminável de equivalências entre equivalências. Discutindo sobre toda a doutrina, você gera uma visão geral de todos os objetos que você marcou com pontos na esfera.
"É apenas uma esfera, mas acontece que, para entender a forma de uma esfera, você precisa entrar no infinito de alguma forma", disse
David Ben-Zvi, da Universidade do Texas em Austin.
Nas últimas décadas do século XX, muitos matemáticos têm trabalhado na teoria das "categorias de infinidades" - no que é capaz de rastrear uma torre infinita de equivalências entre equivalências. Alguns deles alcançaram um sucesso sério. Mas apenas um chegou ao fim.
Reescrevendo a Matemática
O primeiro trabalho de Jacob Lurie nas categorias de infinito não teve muito sucesso. Em 5 de junho de 2003, o cientista de 25 anos publicou um documento de 60 páginas intitulado "
On the Topos of Infinity " no site de preprints científicos arxiv.org. Lá, ele começou a fazer rascunhos das regras pelas quais os matemáticos poderiam trabalhar com categorias de infinito.
Nem todo mundo aceitou o primeiro trabalho da mesma maneira. Pouco depois da leitura,
Peter May , matemático da Universidade de Chicago, escreveu ao supervisor de Lurie, Michael Hopkins, que embora o trabalho de Lurie contenha idéias interessantes, ele parece inacabado e requer uma abordagem mais disciplinada.
"Expliquei nossos comentários a Mike e ele os repassou a Jacob", disse May.
Ainda não se sabe se Lurie aceitou a carta de May como um desafio ou se ele já havia planejado seu próximo passo (Lurie rejeitou vários pedidos de entrevista). É claro que, depois de receber comentários críticos, Lurie atingiu um período de produtividade de vários anos, que mais tarde se tornou lendário.
"Não consigo entrar no cérebro de Jacob e, portanto, não sei exatamente o que ele estava pensando", disse May. "Mas há uma enorme diferença entre o rascunho que analisamos e as versões finais, que já estão em um nível matemático completamente diferente."
Em 2006, Lurie publicou no arxiv.org um rascunho de "Teorias dos Maiores Topos". Neste trabalho monumental, ele criou o aparato necessário para substituir a teoria dos conjuntos por uma nova base para a matemática baseada nas categorias do infinito. "Ele criou literalmente milhares de páginas desse aparato fundamental que todos usamos agora", disse Charles Rezk, matemático da Universidade de Illinois em Urbana-Champaign, que fez um trabalho importante desde o início no desenvolvimento de categorias de infinito. "Não consigo imaginar como é possível criar uma obra como 'Teoria dos Maiores Topos' em uma vida - e ele a criou em dois ou três anos."
Então, em 2011, Lurie deu outro trabalho ainda mais longo. Nele, ele reinventou a álgebra.
A álgebra nos fornece um maravilhoso conjunto de regras formais para manipular equações. Os matemáticos constantemente usam essas regras para provar teoremas. No entanto, a álgebra faz ginástica nas barras fixas do sinal de igual. Remova essas barras, substituindo-as por um conceito mais efêmero de equivalência, e algumas operações se tornarão muito complicadas.
Pegue uma das primeiras regras de álgebra que as crianças aprendem na escola: associatividade. A soma ou o produto de três ou mais números não depende de seu agrupamento: 2 × (3 × 4) = (2 × 3) × 4.
É fácil provar a propriedade associativa para uma lista de três ou mais números se você trabalhar com igualdade. Isso é difícil quando você trabalha mesmo com o conceito de forte equivalência. Mas quando você passa para versões mais sutis da equivalência, com suas intermináveis torres de caminhos conectando os caminhos, mesmo uma regra simples, semelhante à associatividade, se transforma em uma floresta sombria.
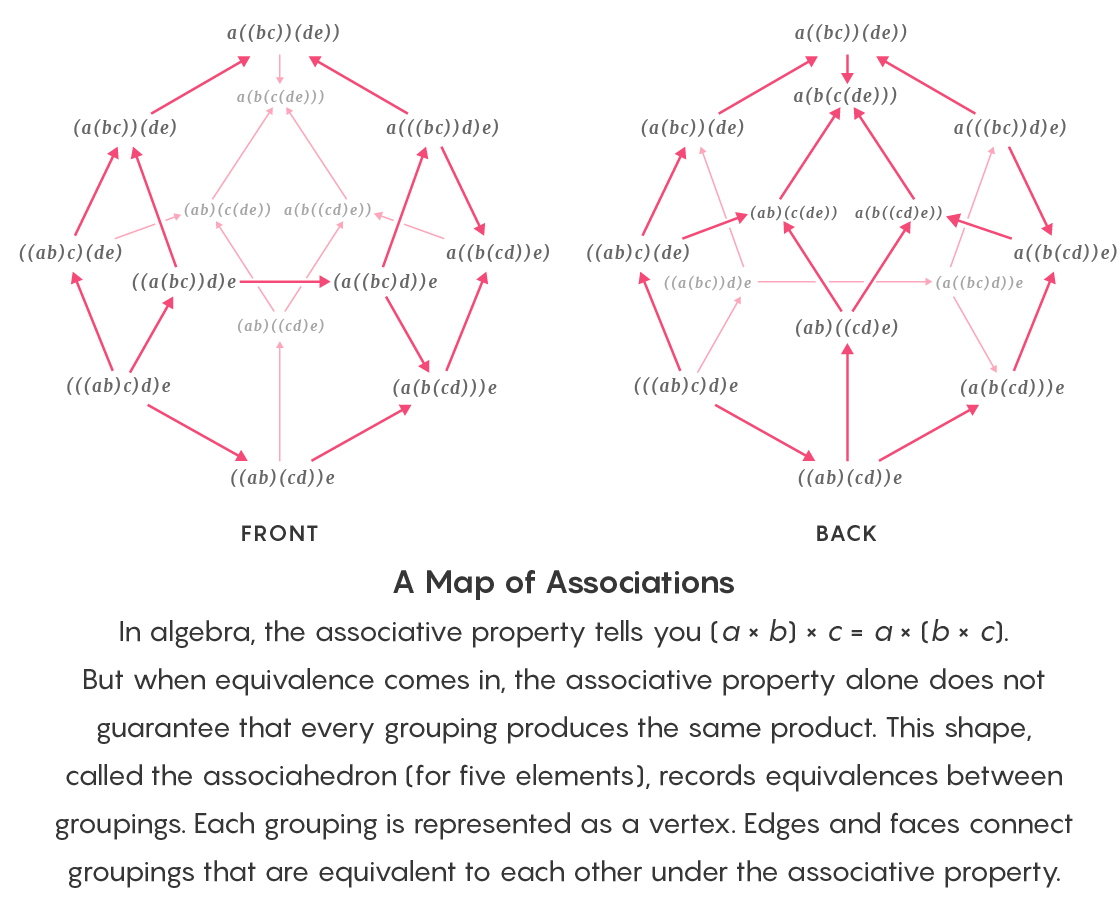Na álgebra, a associatividade afirma que (a × b) × c = a × (b × c). Porém, com o uso da equivalência, a associatividade sozinha não garante que qualquer agrupamento de elementos produza o mesmo resultado de multiplicação. Este assocahedron contém registros de equivalência de grupo. Cada vértice corresponde a um agrupamento. Arestas e faces combinam grupos associativamente equivalentes entre si."Isso torna o problema extremamente complicado, o que torna impossível trabalhar com essa nova versão da matemática", disse David Isla, matemático da Universidade de Montana.
Em Álgebra Superior, cuja versão mais recente se estende por 1553 páginas, Lurie desenvolveu uma opção de associatividade para categorias infinitas - assim como muitos outros teoremas algébricos que juntos formam a base da matemática das equivalências.
Esses dois livros produziram o efeito de uma bomba explodindo; tais obras dão origem a uma revolução científica. "A escala foi extraordinária", disse Reel. "Foi a conquista do nível de
Grothendieck em geometria algébrica."
No entanto, a revolução leva tempo e, como os matemáticos descobriram após a publicação dos livros de Lurie, esses anos podem ser caóticos.
Diger uma vaca
Os matemáticos são considerados pessoas com pensamento inequívoco: a prova é verdadeira ou não; a ideia funciona ou não. No entanto, os matemáticos também são pessoas comuns, e reagem a novas idéias da mesma maneira que as pessoas comuns: subjetivamente, emocionalmente, tendo motivos pessoais.
"Eu acho que muitos textos foram escritos sobre matemáticos em um tom que eles procuram uma verdade clara e cristalina", disse Campbell. "Mas isso não está acontecendo." São pessoas com gostos próprios, zonas de conforto e podem negar coisas de que não gostam por razões estéticas ou pessoais ".
Nesse sentido, o trabalho de Lurie tornou-se um desafio complexo para a comunidade. De fato, foi provocativo: eis uma maneira nova e melhor de fazer matemática. Esta mensagem foi dirigida especialmente aos matemáticos, que passaram toda a sua carreira desenvolvendo métodos que Lurie se destacou.
"As pessoas nem sempre gostam de ver a próxima geração reescrever seu trabalho, e esse processo gera estresse", disse Francis. "Essa é uma das características da teoria das categorias do infinito - a maioria dos trabalhos anteriores corresponde."
O trabalho de Lurie foi difícil de digerir por outros motivos. O volume de materiais significava que os matemáticos teriam que passar anos lendo seus livros. É quase impossível exigir de matemáticos ocupados que estão no meio de uma carreira, e para estudantes de pós-graduação que têm apenas alguns anos para dar um resultado que lhes permita encontrar um emprego, isso é muito arriscado.
O trabalho de Lurie também foi muito abstrato, mesmo em comparação com a natureza extremamente abstrata de tudo o que estudava matemática avançada. E nem todo mundo gostou. "Muitas pessoas pensaram que o trabalho de Lurie era um lixo abstrato e muitas simplesmente se apaixonaram por ela", disse Campbell. "Havia opções intermediárias, incluindo aqueles que não a entendiam."
Emily reelA comunidade científica constantemente percebe novas idéias, mas geralmente isso acontece lentamente e com a sensação de que todos estão se movendo ao mesmo tempo. O surgimento de novas idéias cria dificuldades para o aparato intelectual da comunidade. "Muitas coisas novas surgem imediatamente - é como uma jibóia tentando digerir uma vaca", disse Campbell. "Uma enorme massa passa pela comunidade."
Se você é um matemático que acredita que a abordagem de Lurie é a melhor maneira de fazer matemática, seu caminho a seguir será solitário. Poucas pessoas leem o trabalho de Lurie, não havia livros para recontá-los brevemente e seminários para ajudá-lo a se orientar. "Havia apenas uma maneira de estudar tudo isso em detalhes - sentar e fazer tudo sozinho", disse Peter Heine, estudante de graduação do MIT que passou um ano lendo o trabalho de Lurie. Acho que é o mais difícil. "Não é fácil sentar e descobrir você mesmo - ou seja, sentar e ler 800 páginas da Teoria da Teoria de Topos."Como muitas novas invenções, a teoria dos topos superiores exige que os matemáticos interajam ativamente com o aparelho, o que permite que ele funcione. É assim que cada garoto de 16 anos que sonha com uma carteira de motorista aprende como resolver o problema do motor. "Se houvesse uma versão mais amigável de tudo isso, a teoria se tornaria imediatamente mais acessível a círculos matemáticos mais amplos", disse Dennis Gatesgory, um matemático de Harvard que trabalhou com Lurie.Quando as pessoas começaram a ler o trabalho de Lurie e usar as categorias do infinito em seus estudos, outros problemas surgiram. Os matemáticos construíram seu trabalho com base nas categorias do infinito. Os revisores das revistas receberam esses papéis e perguntaram: o que é?"Havia uma situação em que o trabalho retornava de revistas com críticas absurdas, das quais era visível uma total falta de entendimento ou levou vários anos para publicá-las", disse Barvik. "Isso pode ser muito inconveniente, porque o trabalho não publicado que está no seu site há anos parece cada vez mais ridículo."No entanto, o maior problema não foram os trabalhos não publicados, mas trabalhos usando as categorias de infinito e publicados - mas contendo erros.Os livros de Lurie são a única fonte autorizada de informações sobre as categorias do infinito. Eles são rigorosos, mas é difícil entendê-los completamente. E são especialmente inadequadas para o papel das instruções que podem ser referenciadas - é difícil procurar certos teoremas ou verificar se uma certa aplicação das categorias de infinito encontradas no trabalho de alguém realmente funciona."A maioria dos matemáticos que trabalham neste campo não leu Lurie sistematicamente", disse Andre Joyal, um matemático da Universidade de Quebec, em Montreal, cujo trabalho inicial foi um ingrediente-chave nos livros de Lurie. “Leva muito tempo e energia, então assumimos que tudo o que está escrito em seus livros é verdadeiro - porque quase todas as vezes que verificamos algo, isso acaba sendo verdade. De fato, sempre. "A inacessibilidade dos livros de Lurie levou a imprecisões em alguns dos estudos que se seguiram. Os livros de Lurie são difíceis de ler, difíceis de citar e difíceis de usar para testar o trabalho de outras pessoas."A literatura geral sobre o tema das categorias do infinito parece confusa", disse Zakharevich.Apesar de todo o seu formalismo, a matemática não deve ser um texto sagrado que apenas os padres possam ler. Nesta área, não apenas são necessários grandes volumes, mas também folhetos, não apenas as revelações iniciais, mas também as interpretações de suas descrições. Enquanto isso, a teoria das categorias do infinito existe, na maioria das vezes, na forma de vários livros grandes em uma prateleira."Você pode adotar a abordagem. 'Jacob vai lhe dizer o que fazer e está tudo em ordem", disse Rezk. "Ou você pode decidir que 'não sabemos como apresentar nosso tópico suficientemente bem para que as pessoas possam usá-lo."No entanto, poucos matemáticos foram capazes de aceitar o desafio e tornar a categoria do infinito uma tecnologia que mais pessoas de seu campo de estudo poderiam usar.Teoria Amigável ao Usuário
Para traduzir as categorias de infinitos em um objeto capaz de trabalho matemático real, Lurie teve que provar os teoremas associados a eles. E para isso, ele teve que escolher uma paisagem na qual criar essa evidência - assim como uma pessoa envolvida em geometria, é necessário escolher um sistema de coordenadas para o trabalho. Os matemáticos chamam essa seleção de modelo.Lurie desenvolveu as categorias de infinitos no modelo de quase-categorias. Outros matemáticos antes dele desenvolveram as categorias de infinidades em outros modelos. E, embora o trabalho deles não tenha sido tão abrangente quanto o de Lurie, em algumas situações é mais fácil lidar com eles. "Jacob escolheu um modelo e verificou que tudo funciona nele, mas muitas vezes não é o mais fácil", disse Zakharevich.Na geometria, os matemáticos compreendem claramente como se mover entre diferentes sistemas de coordenadas. Eles também provaram que os teoremas provados em algumas condições funcionam em outras.Para categorias infinitas, essas garantias não existem. No entanto, quando os matemáticos escrevem trabalhos usando as categorias de infinitos, geralmente alternam facilmente entre os modelos, sugerindo (mas não provando) a portabilidade dos resultados. "As pessoas não especificam o que estão fazendo, alternam entre todos esses modelos diferentes e dizem: Ah, é a mesma coisa", disse Heine. "Mas isso não é prova."Nos últimos seis anos, alguns matemáticos tentaram obter essas garantias. Ryl e Dominic Verityda Universidade McUyra, na Austrália, desenvolveu uma maneira de descrever as categorias de infinitos, superando as dificuldades que apareceram em plataformas anteriores usando determinados modelos. Seu trabalho, baseado nos trabalhos anteriores de Barvik e outros, provou que muitos dos teoremas da Teoria dos Topos Superiores permanecem verdadeiros, independentemente do modelo usado. E eles provam essa compatibilidade de maneira apropriada: "Estudamos as categorias do infinito, cujos objetos são elas próprias as categorias do infinito", disse Ril. "A teoria das categorias morde sua cauda."Ril e Verity esperam desenvolver a teoria das categorias de infinitos de outra maneira. Eles escolhem aspectos da teoria que funcionam independentemente do modelo. Tal apresentação, independente do modelo, possui uma qualidade conveniente de aplicabilidade instantânea, que, eles esperam, atrairá matemáticos para esta área de pesquisa que se afastaram dela quando a única entrada foi The The Higher Topos Theory."Para entrar neste mundo, você precisa superar o fosso", disse Hopkins. "E eles fazem isso abaixar a ponte."Ryl e Verity planejam terminar o trabalho no próximo ano. Enquanto isso, Lurie começou recentemente a trabalhar no projeto Kerodon., que ele planejava transformar em uma espécie de livro de referência sobre a teoria da categoria mais alta, semelhante à Wikipedia. Treze anos após a Teoria de Topos formalizar a matemática da equivalência, essas iniciativas tentam refinar e disseminar essas idéias - a fim de tornar a matemática da equivalência mais acessível."O gênio tem um papel importante no desenvolvimento da matemática, mas o conhecimento em si é o resultado do trabalho de toda a comunidade", disse Zhoyal. "O objetivo real do conhecimento é tornar-se conhecimento de toda a comunidade e não pertencer a uma ou duas pessoas."