Seguindo os passos de
“Our won: TopCoder Open 2019”, publico tarefas da faixa Algorithm
(programação esportiva clássica. Em uma hora e meia, você precisa resolver três problemas em Java, C #, C ++ ou Python.)1. Torta para seis
Declaração do problemaO prazo é de 4 segundos.
Você tem uma torta. Visto de cima, o bolo tem a forma de um polígono (estritamente) convexo. Você recebe as coordenadas dos vértices nos números inteiros X e Y.
Você tem cinco amigos. Você deseja dividir o bolo em seis pedaços de área igual (mas não necessariamente da mesma forma). Obviamente, qualquer um pode fazer isso em cinco cortes, mas apenas os profissionais podem fazer isso em três cortes.
Encontre três cortes em linhas retas através de um ponto que dividirá o bolo em seis pedaços do mesmo tamanho. Imprima {x, y, d1, d2, d3}, onde (x, y) é o ponto comum das três seções e d1, d2, d3 são os ângulos de direção das seções em radianos.
Definição deClasse: CakeForSix
Método: corte
Parâmetros: int [], int []
Retorna: double []
Assinatura do método: duplo [] cut (int [] x, int [] y)
(verifique se o seu método é público)
Anotações- A direção positiva ao longo do eixo x é 0 (radiano), a direção positiva ao longo do eixo y é pi / 2 (radiano).
- O corte na direção d é semelhante ao corte na direção pi * k + d para qualquer número inteiro k.
- Você pode emitir qualquer direção, elas não precisam ser de [0, pi).
- A niveladora calculará a área de seus seis pedaços de bolo em duplas. A resposta será aceita se a diferença relativa ou absoluta entre eles for menor que 10 ^ (- 4).
- Mais precisamente, seja X e Y a menor e a maior de suas seis áreas calculadas pela motoniveladora. Sua resposta será aceita se Y <max (X + 10 ^ (- 4), X * 1 + 10 ^ (- 4))).
- (Na versão original do problema, a precisão 1e-7 foi usada em vez de 1e-4. Para resolver esse problema no arquivo morto, o limite de precisão foi reduzido devido à presença de casos de chamada que provavelmente tornam a tarefa insolúvel com precisão 1e-7. Em um mundo ideal, restrições não permita tais casos e ainda exija alta precisão, portanto, resolver o problema com alguma otimização numérica geral não é fácil.)
Limitações- x contém de 3 a 50 elementos, inclusive.
- y contém tantos elementos quanto x.
- todas as coordenadas entre 0 e 10.000, inclusive
- x e y definem um polígono convexo na direção anti-horária.
Original em inglêsDeclaração do Problema
O prazo é de 4 segundos.
Você tem um bolo. Visto de cima, o bolo é um polígono (estritamente) convexo. Você recebe as coordenadas de seus vértices nos int [] sx e y.
Você tem cinco amigos. Agora você deseja cortar o bolo em seis pedaços da mesma área (mas não necessariamente da mesma forma). É claro que qualquer um pode fazer isso em cinco cortes - mas apenas um verdadeiro profissional pode fazer isso em três!
Encontre três cortes retos passando pelo mesmo ponto que cortou o bolo em seis partes igualmente grandes. Retorne {x, y, d1, d2, d3}, onde (x, y) é o ponto comum dos três cortes e d1, d2, d3 são suas direções em radianos.
Definição de
Classe: CakeForSix
Método: corte
Parâmetros: int [], int []
Retorna: double []
Assinatura do método: duplo [] cut (int [] x, int [] y)
(verifique se o seu método é público)
Anotações
- A direção positiva ao longo do eixo x é 0 (radianos), a direção positiva ao longo do eixo y é pi / 2 (radianos).
- Um corte na direção d é o mesmo que um corte na direção pi * k + d para qualquer número inteiro k.
- Você pode retornar todas as direções, elas não precisam ser de [0, pi).
- A motoniveladora calculará as áreas dos seus seis pedaços de bolo em duplas. A resposta será aceita se a diferença relativa ou absoluta entre eles for menor que 10 ^ (- 4).
- Mais precisamente, seja X e Y a menor e a maior de suas seis áreas, conforme calculado pela motoniveladora. Então, sua resposta será aceita se Y <max (X + 10 ^ (- 4), X * (1 + 10 ^ (- 4))).
- (A versão original do problema usava a precisão 1e-7 em vez de 1e-4. Para solucionar esse problema no arquivo morto, o limite de precisão foi reduzido devido à existência de casos de desafio que provavelmente tornam a tarefa insolúvel com precisão 1e-7 Em um mundo ideal, as restrições não permitiriam tais casos e ainda exigiam alta precisão, de modo que não é fácil resolver o problema por meio de uma otimização numérica geral.)
Restrições
- x terá entre 3 e 50 elementos, inclusive.
- y terá o mesmo número de elementos que x.
- Todas as coordenadas estarão entre 0 e 10.000, inclusive.
- x e y descreverão um polígono convexo no sentido anti-horário.
Exemplos
0){0, 20, 30, 50, 30, 20}
{10, 0, 0, 10, 20, 20}
Devoluções:
{24.999999999437453, 9.999999999500002, 0,0, 0,7266423406817211, 2,4149503129080787}
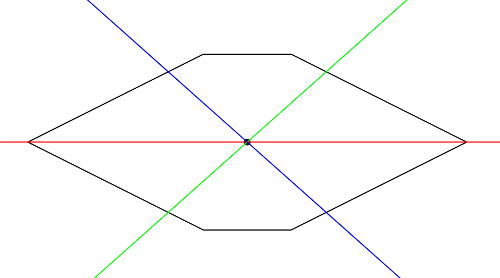
Hexágono simétrico, mas não regular. Um exemplo de resposta corresponde a cortá-la ao meio na horizontal e a fazer outros dois cortes no centro, que dividem cada parte em três partes.
 1)
1){0, 1000, 0}
{0, 0, 1000}
Devoluções:
{333.3333333331763, 333.3333333332546, 0,7853981633986264, 2,0344439357948154, 2,6779450445891753}
Triângulo direito Novamente, podemos começar com um dos três cortes ao longo do eixo da simetria.
 2)
2){40, 70, 90, 90, 50}
{30, 20, 40, 100, 60}
Devoluções:
{69.79517771922892, 52.77575974637605, 2.0616329654335885, 3.637826104091601, 4.32123485812475}
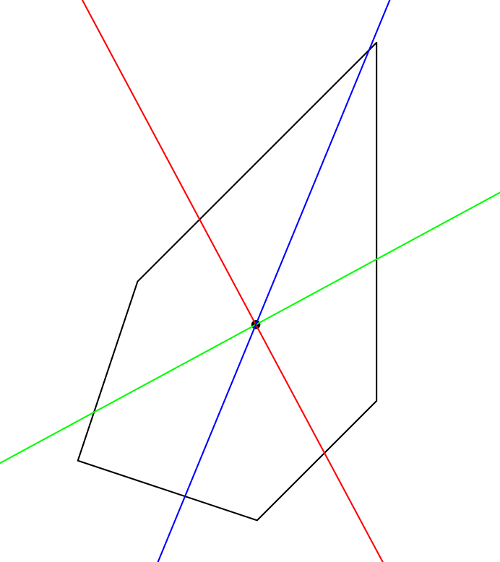
Pentágono errado.
 3)
3){300, 400, 300, 200}
{500, 600, 700, 600}
Retorna: {299.99999999974995, 599.9999999995, 0,0, 1,107148717794088, 2,034443935795705}
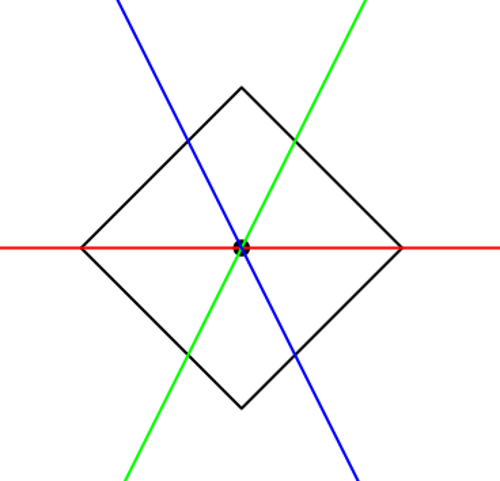
Um quadrado girou 45 graus.
[
Fonte ]