Boa tarde Escrevi este artigo especialmente para os alunos do curso "Algoritmos para desenvolvedores" no OTUS e hoje quero compartilhá-lo com todos os leitores do nosso blog.Um cavalo de xadrez fica em um tabuleiro de xadrez e olha pensativo para o tabuleiro de xadrez.
Quantos movimentos diferentes ele pode fazer?

Louvado seja o inventor do xadrez, existem
64 células no tabuleiro.
Elogio ao arquiteto do computador - o tipo
ulong também possui
64 bits.
Essa coincidência tinha que acontecer!
A idéia brilhante se sugere - armazenar o
quadro inteiro em
um número inteiro ! Existe até um termo especial para esta solução -
Bitboard - um bit board.
Então, como encontrar
rapidamente o número de movimentos de um cavalo de xadrez usando essa idéia?
Dado:
knightNr - número de células do tabuleiro onde o cavalo está (de 0 a 63).
É necessário:
movesCount - o número de campos para onde ele pode ir (de 2 a 8).
Algoritmo
1. Converta o número da gaiola do cavalo em
ulong - valor do painel de bits
knightNr ->
knightBits2. Defina bits para todos os movimentos possíveis do cavalo
knightBits ->
movimentosBits3.Contar o número de bits da unidade
movesBits ->
movesCount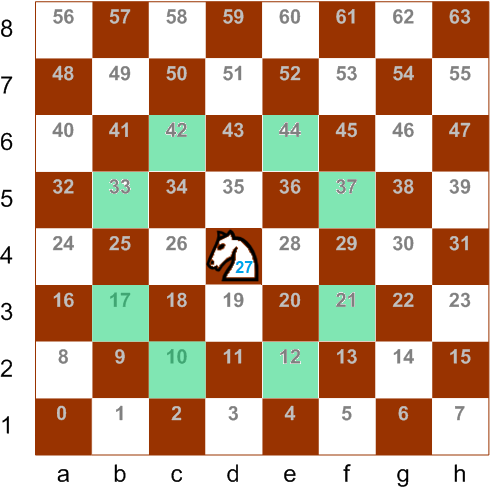
O primeiro passo é muito simples, você precisa mudar o bit zero para a esquerda pelo número especificado de posições.
ulong knightBits = 1 << knightNr;
O segundo passo é um pouco mais complicado. Um cavalo pode ir em 8 direções diferentes. Consideraremos essas compensações não "horizontalmente / verticalmente", mas por posições de bits. Ou seja, consideramos quantas posições você precisa para mudar o bit inicial de cada movimento. Em seguida, adicionamos tudo com uma operação lógica "ou".
Vamos começar a listar os movimentos do lado esquerdo do quadro para a direita:
movesBits = knightBits << 6 | knightBits >> 10
Verdade, legal!?
Infelizmente, existem “buracos negros” nas bordas do quadro. Por exemplo, de acordo com este algoritmo, da célula a4 (bit # 24) você pode chegar à célula g2 (bit # 14 = 24 - 10), esse salto é um
teletransporte de um cavalo de xadrez esférico no vácuo em uma placa através de um buraco negro para os verticais extremos ...
Para excluir o salto quântico do cavalo sobre a borda do tabuleiro, é necessário "desconectar" as faixas extremas após o movimento. Por exemplo, para os movimentos +6 e -10 (duas células à esquerda), é necessário cancelar os valores obtidos nas verticais geh, pois você não pode terminar nessas verticais depois de mover os dois movimentos para a esquerda.
Para fazer isso, precisamos de constantes de grade de 4 bits, nas quais todos os bits são definidos como 1, exceto as verticais indicadas. Ou seja:
ulong nA = 0xFeFeFeFeFeFeFeFe; ulong nAB = 0xFcFcFcFcFcFcFcFc; ulong nH = 0x7f7f7f7f7f7f7f7f; ulong nGH = 0x3f3f3f3f3f3f3f3f;
Nas partes superior e inferior do tabuleiro de xadrez também existem “buracos negros” que absorvem completamente o cavalo, para que não precisem ser verificados separadamente.
Agora, o algoritmo para gerar movimentos permitidos de cavalos se parece com isso:
movesBits = nGH & (knightBits << 6 | knightBits >> 10) | nH & (knightBits << 15 | knightBits >> 17) | nA & (knightBits << 17 | knightBits >> 15) | nAB & (knightBits << 10 | knightBits >> 6);
Funciona muito (!) Rápido.
Alguns ticks - e temos um bitmap de todas as aventuras possíveis a cavalo. O mais surpreendente é que esse algoritmo funciona bem, mesmo que haja vários cavalos no tabuleiro. Ele imediatamente gera todos os movimentos possíveis para todos os cavalos! Verdade, ótimo!?
Resta contar o número de bits
A maneira mais fácil é deslocar o número 1 bit para a direita e contar esses. Dificuldade - 64 operações. Memória - 64 bits.
A maneira mais rápida é criar um cache / matriz com 65536 elementos, nos quais o número de bits para cada índice é gravado de 0 a 65535. E adicione 4 elementos dessa matriz que correspondam aos próximos segmentos de 16 bits do número.
Dificuldade - 4 operações. Memória - 64 kilobytes.
Mas consideraremos a
maneira mais complicada , cuja complexidade é igual ao número de bits únicos no número. Como não há muitos movimentos, essa abordagem será a mais ideal para nós.
Para começar, observamos que, subtraindo uma unidade de um número, transformamos todos os zeros "certos" em unidades e a unidade mais externa em zero:
1001010100010000 - 1 = 1001010100001111
Em seguida, aplique a operação lógica "e" para estes números:
1001010100010000 & 1001010100001111 = 1001010100000000
Como você pode ver, de uma maneira tão complicada, redefinimos a unidade mais à direita para zero. Repita esta operação até obtermos zero como resultado. Quantas iterações, tantos bits únicos. Verdade, ótimo!?
É assim que este algoritmo é escrito na íntegra:
int movesCount = 0; while (movesBits != 0) { movesBits &= (movesBits - 1); movesCount ++; }
O problema está resolvido!
Esta tarefa tem outra solução muito simples e puramente lógica: determinar a distância do cavaleiro da borda do tabuleiro de xadrez (no canto há 2 movimentos, perto da borda há 3 a 6 movimentos, no centro há 8 movimentos). Mas se resolvêssemos o problema dessa maneira, não saberíamos sobre o painel de bits, sobre máscaras de bits verticais, sobre o algoritmo para contar rapidamente bits únicos e sobre buracos negros para cavalos esféricos no vácuo ...
Agora sabemos tudo sobre isso. A vida de um programador de xadrez tornou-se mais rica e significativa, felicidades!
Tarefa faça você mesmo: faça o mesmo para o rei do xadrez.