Geekly articles weekly

Otimização da estratégia de blackjack de Monte Carlo

A tradução do artigo foi preparada especificamente para os alunos do curso Machine Learning .



O treinamento reforçado conquistou o mundo da Inteligência Artificial. A partir do AlphaGo e AlphaStar , um número crescente de atividades que antes eram dominadas por seres humanos agora são conquistadas por agentes de IA com base no treinamento de reforço. Em resumo, essas conquistas dependem da otimização das ações do agente em um ambiente específico para obter a recompensa máxima. Nos últimos artigos do GradientCrescent, analisamos vários aspectos fundamentais do aprendizado reforçado, desde o básico de sistemas de bandidos e abordagens baseadas em políticas até a otimização do comportamento baseado em recompensa em ambientes Markov . Todas essas abordagens exigiram conhecimento completo de nosso ambiente. A programação dinâmica , por exemplo, exige que tenhamos uma distribuição de probabilidade completa de todas as transições de estado possíveis. Entretanto, na realidade, descobrimos que a maioria dos sistemas não pode ser totalmente interpretada e que as distribuições de probabilidade não podem ser obtidas explicitamente devido à complexidade, incerteza inerente ou limitações nas capacidades computacionais. Como analogia, considere a tarefa do meteorologista - o número de fatores envolvidos na previsão do tempo pode ser tão grande que é impossível calcular com precisão a probabilidade.

Para tais casos, métodos de ensino como Monte Carlo são a solução. O termo Monte Carlo é comumente usado para descrever qualquer abordagem para estimativa de amostragem aleatória. Em outras palavras, não prevemos conhecimento sobre o meio ambiente, mas aprendemos com a experiência passando por sequências exemplares de estados, ações e recompensas obtidas como resultado da interação com o meio ambiente. Esses métodos funcionam observando diretamente as recompensas retornadas pelo modelo durante a operação normal para julgar o valor médio de suas condições. É interessante notar que, mesmo sem nenhum conhecimento da dinâmica do ambiente (que deve ser considerada a distribuição de probabilidade das transições de estado), ainda podemos obter um comportamento ideal para maximizar as recompensas.

Como exemplo, considere o resultado de um lançamento de 12 dados. Considerando esses lançamentos como um único estado, podemos calcular a média desses resultados para nos aproximarmos do verdadeiro resultado previsto. Quanto maior a amostra, mais precisamente nos aproximamos do resultado esperado real.


A quantidade média esperada em 12 dados para 60 tiros é 41,57

Esse tipo de avaliação baseada em amostragem pode parecer familiar para o leitor, uma vez que essa amostragem também é realizada para sistemas k-bandit. Em vez de comparar bandidos diferentes, os métodos de Monte Carlo são usados ​​para comparar políticas diferentes em ambientes Markov, determinando o valor do estado conforme uma determinada política é seguida até que o trabalho seja concluído.

Estimativa de Monte Carlo do valor do estado


No contexto do aprendizado por reforço, os métodos de Monte Carlo são uma maneira de avaliar a significância do estado de um modelo, calculando a média dos resultados da amostra. Devido à necessidade de um estado terminal, os métodos de Monte Carlo são inerentemente aplicáveis ​​a ambientes episódicos. Devido a essa limitação, os métodos de Monte Carlo são geralmente considerados "autônomos", nos quais todas as atualizações são realizadas após atingir o estado terminal. Uma analogia simples para encontrar uma saída de um labirinto pode ser dada - uma abordagem autônoma forçaria o agente a chegar ao fim antes de usar a experiência intermediária adquirida, a fim de tentar reduzir o tempo necessário para atravessar o labirinto. Por outro lado, com a abordagem on-line, o agente muda constantemente seu comportamento já durante a passagem do labirinto, talvez ele perceba que os corredores verdes levam a becos sem saída e decidem evitá-los, por exemplo. Discutiremos abordagens on-line em um dos seguintes artigos.

O método Monte Carlo pode ser formulado da seguinte maneira:



Para entender melhor como o método de Monte Carlo funciona, considere o diagrama de transição de estado abaixo. A recompensa para cada transição de estado é exibida em preto, um fator de desconto de 0,5 é aplicado a ela. Vamos deixar de lado o valor real do estado e focar no cálculo dos resultados de um arremesso.


Diagrama de transição de estado. O número do status é mostrado em vermelho, o resultado é preto.
Dado que o estado do terminal retorna um resultado igual a 0, vamos calcular o resultado de cada estado, começando com o estado do terminal (G5). Observe que definimos o fator de desconto como 0,5, o que levará a uma ponderação nos estados posteriores.



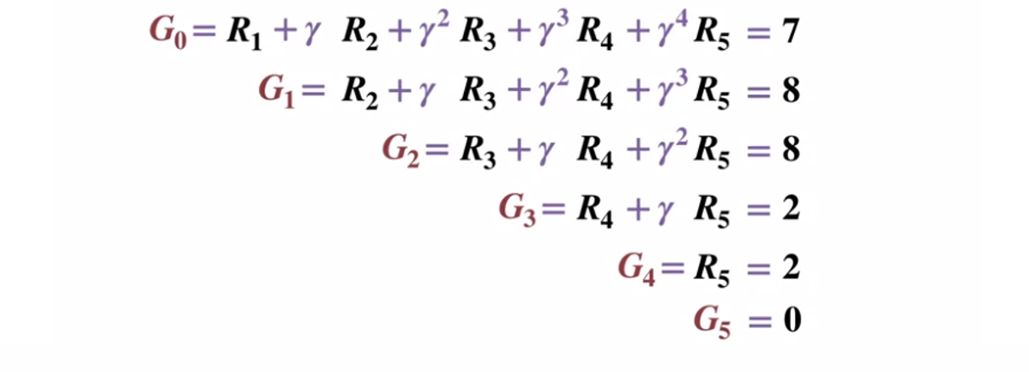
Ou mais geralmente:



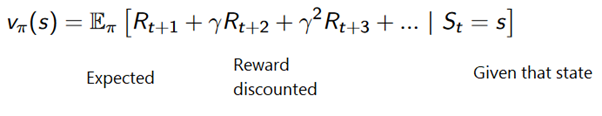
Para evitar o armazenamento de todos os resultados da lista, podemos executar o procedimento de atualização gradual do valor do estado no método Monte Carlo, usando uma equação que tem algumas semelhanças com a descida tradicional do gradiente:


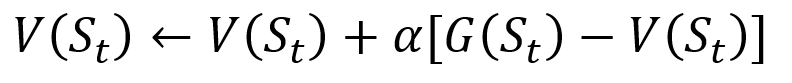Procedimento de atualização incremental de Monte Carlo. S é o estado, V é o seu valor, G é o seu resultado e A é o parâmetro do valor da etapa.

Como parte do treinamento de reforço, os métodos de Monte Carlo podem até ser classificados como Primeira visita ou Toda visita. Em resumo, a diferença entre os dois é quantas vezes um estado pode ser visitado em uma passagem antes da atualização de Monte Carlo. O método de primeira visita de Monte Carlo estima o valor de todos os estados como o valor médio dos resultados após visitas únicas a cada estado antes da conclusão, enquanto o método de cada visita de Monte Carlo calcula a média dos resultados após n visitas até a conclusão. Usaremos a primeira visita de Monte Carlo ao longo deste artigo devido à sua relativa simplicidade.

Gerenciamento de políticas de Monte Carlo


Se o modelo não puder fornecer a política, Monte Carlo poderá ser usado para avaliar os valores da ação do estado. Isso é mais útil do que apenas o significado dos estados, já que a idéia do significado de cada ação (q) em um determinado estado permite que o agente formule automaticamente uma política a partir de observações em um ambiente desconhecido.

Mais formalmente, podemos usar Monte Carlo para estimar q (s, a, pi) , o resultado esperado ao iniciar a partir do estado s, ação ae política subseqüente Pi . Os métodos de Monte Carlo permanecem os mesmos, exceto que há uma dimensão adicional de ações tomadas para um determinado estado. Acredita-se que um par de ação-estado (s, a) seja visitado durante a passagem se o estado s for visitado e a ação a for realizada nele. Da mesma forma, a avaliação das ações de valor pode ser realizada usando as abordagens “Primeira visita” e “Toda visita”.

Como na programação dinâmica, podemos usar uma política de iteração generalizada (GPI) para formar uma política a partir da observação dos valores de ação do estado.



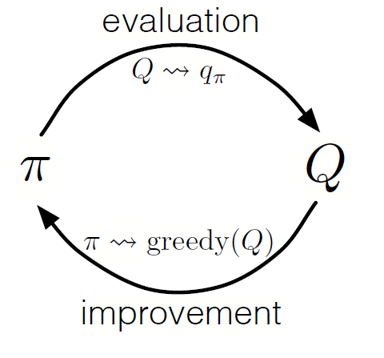
Alternando as etapas de avaliação e aprimoramento de políticas, e incluindo pesquisas para garantir que todas as ações possíveis sejam visitadas, podemos alcançar a política ideal para cada condição. Para o GPI de Monte Carlo, essa rotação geralmente é feita após o final de cada passe.


GPI de Monte Carlo

Estratégia de Blackjack


Para entender melhor como o método de Monte Carlo funciona na prática na tarefa de avaliar vários valores de estado, vamos fazer uma demonstração passo a passo do jogo de blackjack. Para começar, vamos determinar as regras e condições do nosso jogo:

  • Vamos jogar apenas contra o dealer, não haverá outros jogadores. Isso nos permitirá considerar as mãos do revendedor como parte do ambiente.
  • O valor dos cartões com números iguais aos valores nominais. O valor dos cartões de figuras: Valete, Rei e Rainha é 10. O valor do ás pode ser 1 ou 11, dependendo da escolha do jogador.
  • Ambos os lados recebem dois cartões. Duas cartas de jogador estão viradas para cima, uma das cartas do dealer também está virada para cima.
  • O objetivo do jogo é que a quantidade de cartas na mão seja <= 21. Um valor maior que 21 é um fracasso, se ambos os lados têm um valor de 21, o jogo é empatado.
  • Depois que o jogador vê suas cartas e a primeira carta do dealer, o jogador pode escolher uma nova carta ("ainda") ou não ("suficiente") até que ele esteja satisfeito com a soma dos valores das cartas em sua mão.
  • Em seguida, o croupier mostra sua segunda carta - se o valor resultante for menor que 17, ele é obrigado a pegar cartas até atingir 17 pontos, após o que não aceita mais a carta.

Vamos ver como o método Monte Carlo funciona com essas regras.

Rodada 1.


Você ganha um total de 19. Mas você tenta pegar a sorte pela cauda, ​​arriscar, conseguir 3 e ficar sem dinheiro. Quando você faliu, o dealer tinha apenas uma carta aberta com uma soma de 10. Isso pode ser representado da seguinte maneira:



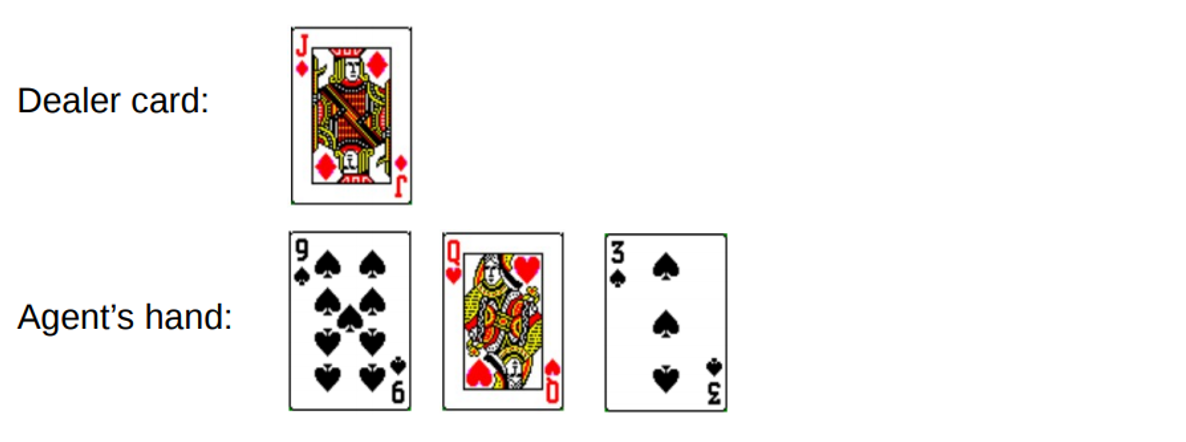
Se ficarmos sem dinheiro, nossa recompensa para a rodada é -1. Vamos definir esse valor como o resultado de retorno do penúltimo estado, usando o seguinte formato [Valor do agente, valor do revendedor, ás?]:



Bem, agora estamos sem sorte. Vamos para outra rodada.

Rodada 2.


Você digita um total de 19. Desta vez, você decide parar. O revendedor disca 13, pega um cartão e fica sem dinheiro. O penúltimo estado pode ser descrito da seguinte maneira.



Vamos descrever as condições e recompensas que recebemos nesta rodada:



Com o final da passagem, agora podemos atualizar os valores de todos os nossos estados nesta rodada usando os resultados calculados. Tomando um fator de desconto de 1, simplesmente distribuímos nossa nova recompensa de mão, como foi feito nas transições de estado anteriores. Como o estado V (19, 10, no) retornou anteriormente -1, calculamos o valor de retorno esperado e o atribuímos ao nosso estado:


Valores finais do estado para demonstração usando o blackjack como exemplo .

Implementação


Vamos escrever um jogo de blackjack usando o método Monte Carlo da primeira visita para descobrir todos os valores de estado possíveis (ou várias combinações disponíveis) no jogo usando Python. Nossa abordagem será baseada na abordagem de Sudharsan et. al. . Como de costume, você pode encontrar todo o código do artigo em nosso GitHub .

Para simplificar a implementação, usaremos o ginásio da OpenAI. Pense no ambiente como uma interface para iniciar o blackjack com uma quantidade mínima de código; isso nos permitirá focar na implementação do aprendizado reforçado. Convenientemente, todas as informações coletadas sobre os estados, ações e recompensas são armazenadas nas variáveis ​​de "observação" , que são acumuladas durante as sessões de jogo atuais.

Vamos começar importando todas as bibliotecas necessárias para obter e coletar nossos resultados.

import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use('ggplot')

Em seguida, vamos inicializar nosso ambiente de academia e definir uma política que coordene as ações de nosso agente. De fato, continuaremos a receber o cartão até que o valor na mão atinja 19 ou mais, após o que paramos.

 #Observation here encompassess all data about state that we need, as well as reactions to it env = gym.make('Blackjack-v0') #Define a policy where we hit until we reach 19. # actions here are 0-stand, 1-hit def sample_policy(observation): score, dealer_score, usable_ace = observation return 0 if score >= 19 else 1

Vamos definir um método para gerar dados de aprovação usando nossa política. Armazenaremos informações sobre o status, as ações executadas e a remuneração pela ação.

 def generate_episode(policy, env): # we initialize the list for storing states, actions, and rewards states, actions, rewards = [], [], [] # Initialize the gym environment observation = env.reset() while True: # append the states to the states list states.append(observation) # now, we select an action using our sample_policy function and append the action to actions list action = sample_policy(observation) actions.append(action) # We perform the action in the environment according to our sample_policy, move to the next state observation, reward, done, info = env.step(action) rewards.append(reward) # Break if the state is a terminal state (ie done) if done: break return states, actions, rewards

Por fim, vamos definir a primeira visita da função de previsão de Monte Carlo. Primeiro, inicializamos um dicionário vazio para armazenar os valores atuais do estado e um dicionário que armazena o número de registros para cada estado em diferentes passagens.

 def first_visit_mc_prediction(policy, env, n_episodes): # First, we initialize the empty value table as a dictionary for storing the values of each state value_table = defaultdict(float) N = defaultdict(int)

Para cada passagem, chamamos nosso método generate_episode para obter informações sobre os valores do estado e as recompensas recebidas após a ocorrência do estado. Também inicializamos a variável para armazenar nossos resultados incrementais. Em seguida, obtemos a recompensa e o valor atual do estado para cada estado visitado durante o passe e aumentamos nossos retornos variáveis ​​pelo valor da recompensa por etapa.

 for _ in range(n_episodes): # Next, we generate the epsiode and store the states and rewards states, _, rewards = generate_episode(policy, env) returns = 0 # Then for each step, we store the rewards to a variable R and states to S, and we calculate for t in range(len(states) — 1, -1, -1): R = rewards[t] S = states[t] returns += R # Now to perform first visit MC, we check if the episode is visited for the first time, if yes, #This is the standard Monte Carlo Incremental equation. # NewEstimate = OldEstimate+StepSize(Target-OldEstimate) if S not in states[:t]: N[S] += 1 value_table[S] += (returns — value_table[S]) / N[S] return value_table

Deixe-me lembrá-lo que, como estamos implementando a primeira visita de Monte Carlo, visitamos um estado de uma só vez. Portanto, fazemos uma verificação condicional no dicionário de estado para ver se o estado foi visitado. Se essa condição for atendida, poderemos calcular o novo valor usando o procedimento definido anteriormente para atualizar os valores de estado usando o método Monte Carlo e aumentar o número de observações para esse estado em 1. Em seguida, repetimos o processo para a próxima passagem para obter o resultado médio. .

Vamos executar o que obtivemos e ver os resultados!

 value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000) for i in range(10): print(value.popitem())


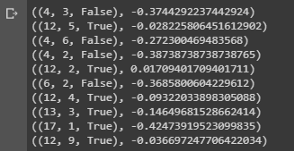Conclusão de uma amostra mostrando os valores de estado de várias combinações nas mãos no blackjack.

Podemos continuar fazendo observações de Monte Carlo para 5000 passes e construindo uma distribuição de valores de estado que descrevem os valores de qualquer combinação nas mãos do jogador e do dealer.

 def plot_blackjack(V, ax1, ax2): player_sum = np.arange(12, 21 + 1) dealer_show = np.arange(1, 10 + 1) usable_ace = np.array([False, True]) state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace))) for i, player in enumerate(player_sum): for j, dealer in enumerate(dealer_show): for k, ace in enumerate(usable_ace): state_values[i, j, k] = V[player, dealer, ace] X, Y = np.meshgrid(player_sum, dealer_show) ax1.plot_wireframe(X, Y, state_values[:, :, 0]) ax2.plot_wireframe(X, Y, state_values[:, :, 1]) for ax in ax1, ax2: ax.set_zlim(-1, 1) ax.set_ylabel('player sum') ax.set_xlabel('dealer sum') ax.set_zlabel('state-value') fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'}) axes[0].set_title('state-value distribution w/o usable ace') axes[1].set_title('state-value distribution w/ usable ace') plot_blackjack(value, axes[0], axes[1])


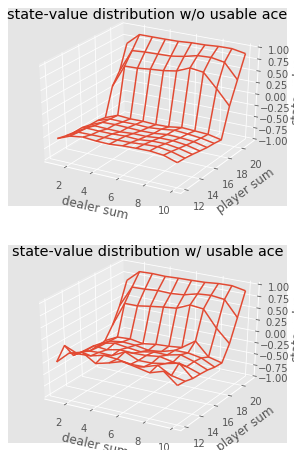Visualização dos valores de estado de várias combinações no blackjack.

Então, vamos resumir o que aprendemos.

  • Os métodos de aprendizado baseados em amostragem nos permitem avaliar valores de estado e estado de ação sem qualquer dinâmica de transição, simplesmente por amostragem.
  • As abordagens de Monte Carlo são baseadas em amostragem aleatória do modelo, observando as recompensas retornadas pelo modelo e coletando informações durante a operação normal para determinar o valor médio de seus estados.
  • Usando métodos de Monte Carlo, é possível uma política de iteração generalizada.
  • O valor de todas as combinações possíveis nas mãos do jogador e do dealer no blackjack pode ser estimado usando várias simulações de Monte Carlo, abrindo caminho para estratégias otimizadas.

Isso conclui a introdução ao método Monte Carlo. Em nosso próximo artigo, seguiremos para métodos de ensino da forma Aprendizado das diferenças temporais.

Fontes:


Sutton et. Aprendizagem por Reforço
White et. Fundamentos da Aprendizagem por Reforço, Universidade de Alberta
Silva et. Aprendizagem por Reforço, UCL
Platt et. Al, Northeaster University

Só isso. Vejo você no curso !

Source: https://habr.com/ru/post/pt477042/

More articles:


All Articles