A otimização dos compiladores é a base do software moderno: eles permitem que os programadores escrevam código em um idioma que entendam e depois o convertam em código que possa ser executado com eficiência por equipamentos. A tarefa de otimizar os compiladores é entender o que o programa de entrada que você escreveu faz e criar um programa de saída que faça a mesma coisa, apenas mais rapidamente.
Neste artigo, examinaremos algumas das técnicas básicas de inferência na otimização de compiladores: como projetar um programa com o qual o compilador possa trabalhar facilmente; que reduções podem ser feitas no seu programa e como usá-las para reduzi-lo e acelerá-lo.
Os otimizadores de programa podem ser executados em qualquer lugar: como uma etapa de um grande processo de compilação (
Scala Optimizer ); como um programa separado, lançado após o compilador e antes da execução (
Proguard ); ou como parte de um ambiente de tempo de execução que otimiza um programa durante sua execução (
compilador JVM JIT ). As limitações no trabalho dos otimizadores variam de acordo com a situação, mas eles têm apenas uma tarefa: pegar o programa de entrada e convertê-lo no programa de saída, que faz a mesma coisa, mas mais rápido.
Primeiro, examinaremos alguns exemplos de otimizações do rascunho do programa, para que você entenda o que os otimizadores costumam fazer e como fazer tudo manualmente. Em seguida, consideraremos várias maneiras de apresentar programas e, finalmente, analisaremos os algoritmos e técnicas com os quais você pode analisar programas e depois torná-los menores e mais rápidos.
Projeto de programa
Todos os exemplos serão dados em Java. Essa linguagem é muito comum e compila em um montador relativamente simples -
Java Bytecode . Portanto, criaremos uma boa base, graças à qual podemos explorar técnicas de otimização de compilação usando exemplos reais e executáveis. Todas as técnicas descritas abaixo são aplicáveis em quase todas as outras linguagens de programação.
Primeiro, considere um rascunho do programa. Ele contém várias lógicas, registra o resultado padrão dentro do processo e retorna o resultado calculado. O programa em si não faz sentido, mas será usado como uma ilustração do que pode ser otimizado, mantendo o comportamento existente:
static int main(int n){ int count = 0, total = 0, multiplied = 0; Logger logger = new PrintLogger(); while(count < n){ count += 1; multiplied *= count; if (multiplied < 100) logger.log(count); total += ackermann(2, 2); total += ackermann(multiplied, n); int d1 = ackermann(n, 1); total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Por enquanto, assumimos que este programa é tudo o que temos, e nenhuma outra parte do código o chama. Simplesmente insere dados em
main , executa e retorna o resultado. Agora vamos otimizar este programa.
Exemplos de otimização
Tipo de fundição e embutimento
Você deve ter notado que a variável
logger possui um tipo impreciso: apesar do rótulo
Logger , com base no código, podemos concluir que esta é uma subclasse específica -
PrintLogger :
- Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger();
Agora sabemos que o
logger é
PrintLogger e sabemos que chamar
logger.log pode ter uma única implementação. Você pode incorporar:
- if (multiplied < 100) logger.logcount(); + if (multiplied < 100) System.out.println(count);
Isso reduzirá o programa removendo a classe
ErrLogger desnecessária que não é usada e excluindo vários métodos
public Logger log public Logger , uma vez que o inserimos em um único local da chamada.
Constantes de coagulação
Durante a execução do programa,
count e alteração
total , mas
multiplied não: inicia em
0 e é multiplicada cada vez através da
multiplied = multiplied * count , permanecendo igual a
0 . Portanto, você pode substituí-lo em todo o programa por
0 :
static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Como resultado, vemos que
d1 * multiplied sempre
0 , o que significa que o
total += d1 * multiplied não faz nada e pode ser excluído:
- total += d1 * multiplied
Remoção de Código Morto
Depois de dobrar
multiplied e perceber que o
total += d1 * multiplied não faz nada, você pode remover a definição de
int d1 :
- int d1 = ackermann(n, 1);
Isso não faz mais parte do programa, e como o
ackermann é uma função pura, a desinstalação não afetará o resultado do programa.
Da mesma forma, após
logger.log , o próprio
logger não é mais usado e pode ser removido:
- PrintLogger logger = new PrintLogger();
Remoção de Filiais
Agora, a primeira transição condicional em nosso ciclo depende de
0 < 100 . Como isso sempre é verdade, você pode simplesmente remover a condição:
- if (0 < 100) System.out.println(count); + System.out.println(count);
Qualquer transição condicional que seja sempre verdadeira pode estar embutida no corpo da condição e, para transições sempre incorretas, você pode excluir a condição junto com seu corpo.
Cálculo parcial
Agora, analisamos as três chamadas restantes para
ackermann :
total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count);
- O primeiro tem dois argumentos constantes. A função é pura e, mediante cálculo preliminar,
ackermann(2, 2) deve ser igual a 7. - A segunda chamada possui um argumento constante
0 e um n desconhecido. Você pode passá-lo para a definição de ackermann , e acontece que quando m é 0 , a função sempre retorna n + 1.
- Na terceira chamada, os dois argumentos são desconhecidos:
n count . Vamos deixá-los no lugar por enquanto.
Dado que a chamada para
ackermann é definida da seguinte forma:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Você pode simplificá-lo para:
- total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count);
Agendamento tardio
A definição de
d2 usada apenas no
if (count % 2 == 0) condicional
if (count % 2 == 0) . Como o cálculo do
ackermann é limpo, você pode transferir esta chamada para uma
ackermann condicional para que não seja processada até que seja usada:
- int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + }
Isso evitará metade das chamadas para
ackermann(n, count) , acelerando a execução do programa.
Para comparação, a função
System.out.println não está limpa, o que significa que não pode ser transferida dentro ou fora de saltos condicionais sem alterar a semântica do programa.
Resultado otimizado
Depois de coletar todas as otimizações, obtemos o seguinte código-fonte:
static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Embora tenhamos otimizado manualmente, tudo isso pode ser feito automaticamente. A seguir, é apresentado o resultado descompilado do otimizador de protótipo que escrevi para os programas da JVM:
static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {}
O código descompilado é um pouco diferente da versão otimizada manualmente. Algo que o compilador não pôde otimizar (por exemplo, uma chamada não utilizada para o
new PrintLogger ), mas algo foi feito de maneira um pouco diferente (por exemplo,
ackermann e
ackermann__I__TI1__I ). Mas, quanto ao resto, o otimizador automático fez a mesma coisa que eu, usando a lógica incorporada nele.
Surge a pergunta: como?
Visualizações intermediárias
Se você tentar criar seu próprio otimizador, a primeira pergunta que surgir será talvez a mais importante: o que é um "programa"?
Sem dúvida, você está acostumado a escrever e alterar programas na forma de código-fonte. Você definitivamente os executou na forma de binários compilados, talvez até depure os binários. Você pode encontrar programas na forma de uma
árvore de sintaxe ,
código de três endereços ,
A-Normal ,
Estilo de passagem de continuação ou
Atribuição estática única .
Há um zoológico inteiro de diferentes representações de programas. Aqui discutiremos as maneiras mais importantes de representar um "programa" dentro do otimizador.
Código fonte
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
O código fonte não compilado também é uma representação do seu programa. É relativamente compacto, legível por humanos, mas tem duas desvantagens:
- O código fonte contém todos os detalhes dos nomes e formatação, importantes para o programador, mas inúteis para o computador.
- Existem muitos outros programas errados na forma de código-fonte do que os corretos e, durante a otimização, você precisa garantir que seu programa seja convertido do código-fonte de entrada correto para o código-fonte de saída correto.
Esses fatores dificultam o otimizador de trabalhar com o programa na forma de código-fonte. Sim, você
pode converter esse programa, por exemplo, usando
expressões regulares para identificar e substituir padrões. No entanto, o primeiro dos dois fatores dificulta a identificação confiável de padrões com uma abundância de detalhes estranhos. E o segundo fator aumenta muito a chance de ficar confuso e obter um programa resultante incorreto.
Essas restrições são aceitáveis para conversores de programas executados sob supervisão humana, por exemplo, quando você pode usar o
Codemod para refatorar e transformar a base de código. No entanto, você não pode usar o código-fonte como modelo principal de um otimizador automatizado.
Árvores de sintaxe abstrata
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) )

Árvores de sintaxe abstratas (AST) é outro formato intermediário comum. Eles estão localizados na próxima etapa da escada de abstração em comparação com o código-fonte. Normalmente, o AST descarta toda formatação, recuo e comentários do código-fonte, mas mantém os nomes das variáveis locais que são descartadas em representações mais abstratas.
Assim como o código-fonte, o AST sofre com a possibilidade de codificar informações desnecessárias que não afetam a semântica real do programa. Por exemplo, os dois fragmentos de código a seguir são semanticamente idênticos; eles diferem apenas nos nomes das variáveis locais, mas ainda têm ASTs diferentes:
static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) )
O ponto principal é que, embora os ASTs tenham uma estrutura em árvore, eles contêm nós que se comportam semanticamente não como árvores: os valores de
Ident("r") e
Ident("s") determinados não pelo conteúdo de suas subárvores, mas pelos nós de
Assign("r", ...) upstream
Assign("r", ...) e
Assign("s", ...) . De fato, existem relacionamentos semânticos adicionais entre
Ident e
Assign que são tão importantes quanto as arestas na estrutura da árvore AST:

Essas conexões formam uma estrutura gráfica generalizada, incluindo ciclos na presença de definições recursivas de funções.
Bytecode
Como escolhemos o Java como idioma principal, os programas compilados são salvos como bytecode Java nos arquivos .class.
Lembre-se de nossa função
ackermann :
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Ele é compilado neste bytecode:
0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn
A Java Virtual Machine (JVM), que executa o bytecode Java, é uma máquina com uma combinação de uma pilha e registra: há uma pilha de operandos (STACK) na qual os valores são manipulados e uma matriz de variáveis locais (LOCALS) na qual esses valores podem ser armazenados. A função começa com N parâmetros nos primeiros N slots de variáveis locais. À medida que é executada, a função move os dados para a pilha, opera sobre eles, os coloca de volta nas variáveis, chamando
return para retornar o valor ao chamador da pilha de operandos.
Se você anotar o bytecode acima para representar valores que se movem entre a pilha e a tabela de variáveis locais, ele terá a seguinte aparência:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Aqui, usando
a0 e
a1 apresentei os argumentos para a função, que são armazenados na tabela LOCALS no início da função.
1 representa constantes carregadas via
iconst_1 e da
v1 à
v7 , valores intermediários calculados. Existem três instruções de retorno retornando
v1 ,
v3 e
v7 . Esta função não define outras variáveis locais, portanto a matriz LOCALS armazena apenas argumentos de entrada.
Acima, vimos duas variantes de nossa função -
ackermannA e
ackermannB . Então eles olham no bytecode:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| |
Como o código-fonte pega dois argumentos e os coloca em variáveis locais, o bytecode possui as instruções correspondentes para carregar os valores dos argumentos dos índices LOCAL 0 e 1 e salvá-los nos índices 2 e 3. No entanto, o bytecode não está interessado nos nomes de suas variáveis locais: ele funciona com por eles exclusivamente como com índices na matriz LOCALS. Portanto,
ackermannA e
ackermannB terão bytecodes idênticos. Isso é lógico, porque eles são semanticamente equivalentes!
No entanto,
ackermannA e
ackermannB não são compilados no mesmo bytecode que o
ackermann original: embora o bytecode seja abstraído dos nomes das variáveis locais, ele ainda não abstrai completamente o carregamento e o salvamento nessas variáveis. Ainda é importante para nós como os valores se movem ao longo de LOCALS e STACK, embora não afetem o comportamento real do programa.
Além da falta de abstração do carregamento / salvamento, o bytecode tem outra desvantagem: como a maioria dos montadores lineares, ele é muito otimizado em termos de compactação e pode ser muito difícil modificá-lo quando se trata de otimizações.
Para deixar mais claro, vejamos o bytecode da função
ackermann original:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Vamos fazer uma mudança grosseira: deixe a função chamar
30: invokestatic ackermann:(II)I Não uso seu primeiro argumento. E então essa chamada pode ser substituída pela chamada equivalente
30: invokestatic ackermann2:(I)I , que usa apenas um argumento. Essa é uma otimização comum, que permite usar a "remoção de código morto" para descartar qualquer código usado para calcular o primeiro argumento
30: invokestatic ackermann:(II)IPara fazer isso, precisamos não apenas substituir a instrução
30 , mas também olhar a lista de instruções e entender onde o primeiro argumento é calculado (
v4 em
STACK ) e também excluí-lo. Retornamos das instruções
30 a
22 e
22 a
21 e
20 . A versão final:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Ainda podemos fazer uma alteração tão simples em uma função
ackermann simples. Mas nas grandes funções usadas em projetos reais, será muito mais difícil fazer inúmeras mudanças interconectadas. Em geral, qualquer pequena alteração semântica no seu programa pode exigir várias alterações em todo o bytecode.
Você pode notar que fizemos a alteração descrita acima analisando os valores em LOCALS e STACK: observamos como a
v4 passada para a instrução
30 da instrução
22 e
22 leva os dados para
a0 e
1 , que vêm das instruções
21 e
20 . Estes valores são transferidos entre LOCALS e STACK de acordo com o princípio do gráfico: da instrução que calcula o valor para o local de seu uso posterior.
Como os pares
Ident /
Assign em nossos ASTs, os valores passados entre LOCALS e STACK formam um gráfico entre os pontos de cálculo dos valores e os pontos de seu uso. Então, por que não começamos a trabalhar diretamente com o gráfico?
Gráficos de fluxo de dados
Os gráficos de fluxo de dados são o próximo nível de abstração após o bytecode. Se expandirmos nossa árvore de sintaxe com relacionamentos
Ident /
Assign , ou se rastrearmos como o bytecode move valores entre LOCALS e STACK, podemos criar um gráfico. Para a função
ackermann é assim:

Diferentemente do bytecode AST ou Java stack-bytecode, os gráficos de fluxo de dados não usam o conceito de uma “variável local”: em vez disso, o gráfico contém conexões diretas entre cada valor e onde é usado. Ao analisar o bytecode, muitas vezes é necessário interpretar abstratamente LOCALS e STACK para entender como os valores se movem; A análise AST envolve rastrear a árvore e trabalhar com uma tabela de símbolos contendo associações de
Ident /
Ident ; e analisar os gráficos de fluxo de dados geralmente é um rastreamento direto das transições - a pura idéia de "mover valores" sem a casca de apresentar um programa.
Também
ackermann mais fácil manipular os
ackermann que o bytecode linear: substituir um nó pela chamada
ackermann chamada
ackermann e
ackermann2 um dos argumentos é apenas mudar o nó do gráfico (marcado em verde) e excluir um dos links de entrada junto com os nós de trânsito (marcados em vermelho):

Como você pode ver, uma pequena alteração no programa (substituindo
ackermann(int n, int m) por
ackermann2(int m) ) se transforma em uma alteração relativamente localizada no gráfico do fluxo de dados.
Em geral, trabalhar com gráficos é muito mais fácil do que com bytecode linear ou AST: eles são fáceis de analisar e alterar.
Não há muitos detalhes nesta descrição dos gráficos: além da representação física real do gráfico, existem muitas outras maneiras de modelar o controle de estado e fluxo, que são mais difíceis de trabalhar com e além do escopo do artigo. Também omiti vários detalhes sobre a transformação de gráficos, por exemplo, adição e remoção de links, transições para frente e para trás, transições horizontais e verticais (em largura e profundidade), etc. Se você estudou algoritmos, tudo isso deve lhe ser familiar. .
Finalmente, omitimos os algoritmos de conversão de bytecode linear para gráfico e, em seguida, do gráfico de volta para bytecode. Isso por si só é uma tarefa interessante, mas deixamos para você um estudo independente.
Análise
Depois de termos a idéia do programa, precisamos analisá-lo: descubra alguns fatos que permitirão transformar o programa sem alterar seu comportamento. Muitas das otimizações discutidas acima são baseadas na análise do programa:
- Dobragem constante: o resultado da expressão está trabalhando com um valor constante conhecido? O cálculo da expressão é puro?
- Tipo de conversão e inlining: uma chamada de método é do tipo com uma única implementação do método chamado?
- : ?
- : «»? - ? ?
- : , ?
, , , . , , , .
, , , — , . .
(Inference Lattice)
, . , «» - :
Integer ? String ? Array[Float] ? PrintLogger ?
CharSequence ? String , - StringBuilder ?
Any , , ?
:

: ,
"hello" String ,
String CharSequence .
"hello" , (Singleton Type) — . :

, , . , . , , ,
String StringBuilder , , :
CharSequence . ,
0 ,
1 ,
2 , ,
Integer .

, , :

, , . , .
count
main :
static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; }
ackermann ,
count ,
multiplied logger . :

,
count 0 block0 .
block1 , ,
count < n : ,
block3 return ,
block2 ,
count 1 count ,
block1 . ,
< false ,
block3 .
?
block0 . , count = 0.
block1 , , n ( , Integer ), , if . block2 block3.block3 , , block1b , block2 , , block1c . , block2 count , 1 count.- ,
count 0 1 : count Integer. - :
block1 n count Integer .
block2 , count Integer + 1 -> Integer . , count Integer , .
multiplied
,
multiplied :
block0 . , multiplied 0.
block1 , , . block2 block3 ( ).
block2 , block2 ( 0 ) count ( Integer ). 0 * Integer -> 0 , multiplied 0.
block1 block2 . multiplied 0 , .
multiplied 0 , , :
multiplied < 100 true.
if (multiplied < 100) logger.log(count); logger.log(count) .
- ,
multiplied , , 0 .
:

:

:
static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; }
, , , , .
multiplied -> 0 , , . , , . , .
, . :
count ,
multiplied . ,
multiplied count ,
count multiplied . , .
, — : , . , ( ) . .
while , ,
O( ) . (, ) , , .
, .
, . , , , , .
. :
static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; }
:

main :
main(n)
called(n, 0)
called(n, 0) 0
main(n) 0
, , . .
,
called(n, 0) 0 , :

:
static int main(int n){ return 0; }
: A B, C, D, D C, B, D A. A B B A, A A, , !
, Java:
public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } }
n int ,
Any : . ,
factorial int (
Integer ).
factorial ,
factorial factorial , ! ?
Bottom
Bottom :

« , , ».
Bottom factorial :

block0 . n Integer , 1 1 , n == 1 , true false .
true : return 1 .
false n - 1 n Integer .
factorial — , Bottom .
* n: Integer factorial : Bottom Bottom .
return Bottom .factorial 1 Bottom , 1 .
1 factorial , Bottom .
Integer * 1 Integer .
return Integer .factorial Integer 1 , Integer .
factorial , Integer . * n: Integer factorial: Integer , Integer , .
factorial Integer , , .
, .
Bottom , , .
* :
(n: Integer) * (factorial: Bottom)
(n: Integer) * (factorial: 1)
(n: Integer) * (factorial: Integer)
multiplied ,
O( ) . , , .
— , « ». , (« »), , (« »). .
main :
static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; }
,
if (multiplied > 100) multiplied *= count multiplied *= 2 . .
, :
multiplied > 100 true , count += 1 («»).
total , («»).
, :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
, .
:

, , :
block0 ,
block1 , ,
block1b , ,
block1c , ,
return block3 .
,
multiplied -> 0 , :

:

,
block1b (
0 > 100 )
true .
false block1c (
if ):
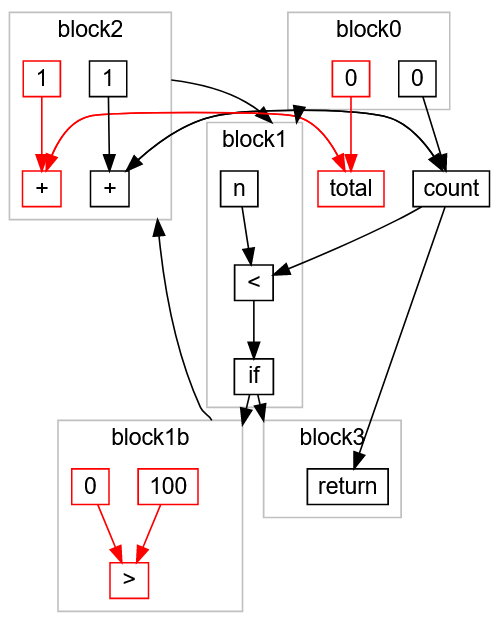
, « »
total > , - , , . ,
return ,
:
> ,
100 ,
0 block1b ,
total ,
0 ,
+ 1 ,
total block0 block2 . :

«» :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
Conclusão
:
- -.
- , .
- , . .
- : «» «» , , .
- : , .
- , .
, , .
, . . , :