Continuo publicando minhas palestras, originalmente destinadas a estudantes que estudam na especialidade de "geologia digital". Esta é a terceira publicação do ciclo no hub, o primeiro artigo foi introdutório e não precisa ser lido. No entanto, para entender este artigo, é necessário ler a introdução aos sistemas lineares de equações, mesmo que você saiba o que é, pois vou me referir muito a exemplos desta introdução.

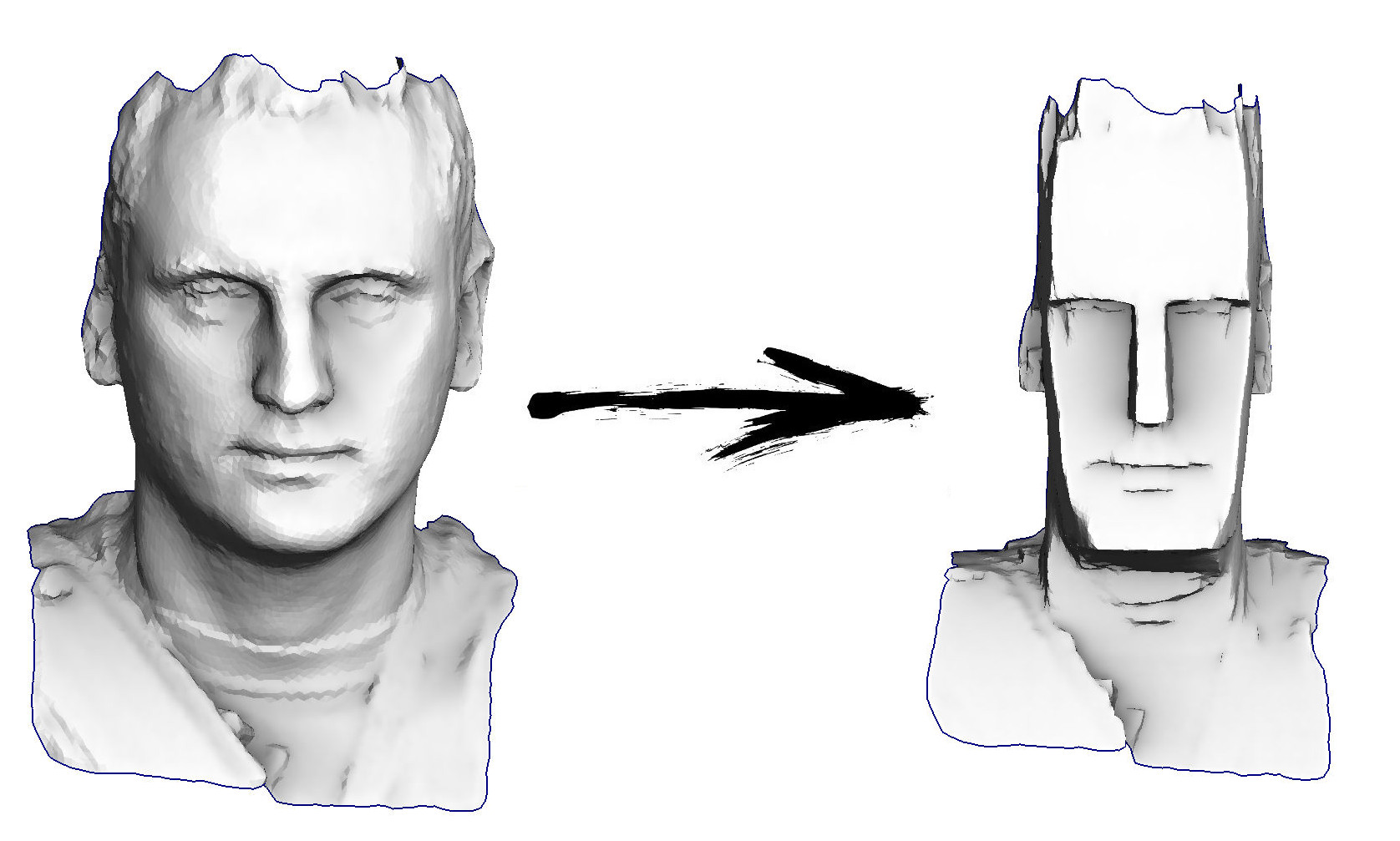
Então, a tarefa de hoje: aprender o processamento geométrico mais simples, por exemplo, ser capaz de transformar minha cabeça em um ídolo da Ilha de Páscoa:



Plano de aula atual:

• Programa educacional sobre teoria das probabilidades (artigo introdutório, opcional)
  
• Introdução aos sistemas lineares de equações
  
• Minimização de formas quadráticas e exemplos de problemas de OLS
  
• Dos mínimos quadrados às redes neurais
  

O repositório oficial do curso mora aqui . O livro ainda não terminou, estou lentamente compilando artigos publicados no Habré.

Neste artigo, minha principal ferramenta será encontrar o mínimo de funções quadráticas; mas antes de começarmos a usar essa ferramenta, você precisa entender pelo menos onde ele tem o botão liga / desliga. Primeiro, atualize a memória e recorde o que são matrizes, o que é um número positivo e também o que é uma derivada.

Matrizes e números

Neste texto, utilizarei abundantemente a notação matricial, então vamos lembrar o que é. Não procure mais no texto, faça uma pausa por alguns segundos e tente formular o que é uma matriz.

Diferentes interpretações matriciais

A resposta é muito simples. A matriz é apenas um armário no qual o raiz-forte é armazenado. Cada merda está em sua célula, as células são agrupadas em linhas em linhas e colunas. No nosso caso particular, os números reais usuais são uma porcaria; é mais fácil para um programador apresentar uma matriz $$$A$ como algo

float A[m][n]; 

Por que esses armazenamentos são necessários? O que eles descrevem? Talvez eu te chateie, mas a matriz em si não descreve nada, ela armazena. Por exemplo, nele você pode armazenar os coeficientes de qualquer função. Vamos esquecer as matrizes por um segundo e imaginar que temos um número $$$a$ . O que isso significa? Sim, o diabo sabe ... Por exemplo, pode ser um coeficiente dentro de uma função que recebe um número como entrada e fornece outro número como saída:

$$

$$f (x): \ mathbb R \ rightarrow \ mathbb R$$

Um matemático poderia escrever uma versão dessa função como

$$

$$f (x) = ax$$

Bem, no mundo dos programadores, ficaria assim:

 float f(float x) { return a*x; } 

Por outro lado, por que tal função e não outra? Vamos dar outro!

$$

$$f (x) = ax ^ 2$$

Desde que comecei sobre programadores, devo escrever o código dela :)

 float f(float x) { return x*a*x; } 

Uma dessas funções é linear e a segunda é quadrática. Qual deles está correto? Não, o próprio número $$$a$ não define, apenas armazena algum valor! De que função você precisa, crie uma assim.

O mesmo acontece com as matrizes, são armazenamentos necessários caso não haja números únicos suficientes (escalares), uma espécie de expansão de números. Acima das matrizes, assim como os números, são definidas as operações de adição e multiplicação.

Vamos imaginar que temos uma matriz $$$A$ Por exemplo, tamanho 2x2:

$$

$$A = \ begin {bmatrix} a_ {11} e a_ {12} \\ a_ {21} e a_ {22} \ end {bmatrix}$$

Essa matriz em si não significa nada, por exemplo, pode ser interpretada como uma função

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2, \ quad f (x) = Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

Essa função converte um vetor bidimensional em um vetor bidimensional. Graficamente, é conveniente apresentar isso como conversão de imagem: damos a imagem à entrada e, na saída, obtemos sua versão esticada e / ou girada (possivelmente até espelhada!). Muito em breve darei uma imagem com vários exemplos dessa interpretação de matrizes.

E pode a matriz $$$A$ imagine como uma função que converte um vetor bidimensional em um escalar:

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R, \ quad f (x) = x ^ \ top A x = \ soma \ limites_i \ soma \ limites_j a_ {ij} x_i x_j$$

Note que a exponenciação não é muito definida com vetores, então não posso escrever $$$x ^ 2$ , como ele escreveu no caso de números comuns. Eu recomendo para aqueles que não estão acostumados a manipular facilmente as multiplicações de matriz, mais uma vez, lembre-se da regra de multiplicação de matriz e verifique se a expressão $$$x ^ \ top A x$ geralmente permitido e realmente fornece um escalar na saída. Para fazer isso, por exemplo, você pode colocar colchetes explicitamente $$$x ^ \ top A x = (x ^ \ top A) x$ . Lembro que temos $$$x$ Como um vetor da dimensão 2 (armazenado em uma matriz da dimensão 2x1), escrevemos explicitamente todas as dimensões:

$$

$$\ underbrace {\ underbrace {\ left (\ underbrace {x ^ \ top} _ {1 \ times 2} \ times \ underbrace {A} _ {2 \ times 2} \ right)} _ {1 \ times 2} \ times \ underbrace {x} _ {2 \ times 1}} _ {1 \ times 1}$$

Voltando ao mundo quente e macio dos programadores, podemos escrever a mesma função quadrática da seguinte forma:

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

O que é um número positivo?

Agora vou fazer uma pergunta muito estúpida: o que é um número positivo? Temos mais uma ótima ferramenta chamada predicado $$$>$ . Mas não se apresse em responder esse número $$$a$ positivo se e somente se $$$a> 0$ Isso seria fácil demais. Vamos definir positividade da seguinte maneira:

Definição 1

Número $$$a$ positivo se e somente se para todos os reais diferentes de zero $$$x \ in \ mathbb R, \ x \ neq 0$ a condição é satisfeita $$$ax ^ 2> 0$ .

Parece bastante complicado, mas se aplica perfeitamente às matrizes:

Definição 2

Matriz quadrada $$$A$ é chamado de definitivo positivo se, para qualquer valor diferente de zero $$$x$ a condição é satisfeita $$$x ^ \ top A x> 0$ isto é, a forma quadrática correspondente é estritamente positiva em todos os lugares, exceto na origem.

Por que preciso de positividade? Como mencionei no início do artigo, minha principal ferramenta será procurar os mínimos de funções quadráticas. Mas, pelo menos para pesquisar, não seria ruim se existisse! Por exemplo, uma função $$$f (x) = - x ^ 2$ obviamente, o mínimo não existe, pois o número -1 não é positivo e $$$f (x)$ diminui infinitamente com o crescimento $$$x$ : ramos de uma parábola $$$f (x)$ olhe para baixo. Matrizes definidas positivas são boas, pois as formas quadráticas correspondentes formam um parabolóide com um mínimo (único). A ilustração a seguir mostra sete exemplos diferentes de matrizes. $$$2 \ vezes 2$ , positivo definido e simétrico, e não. Linha superior: interpretação de matrizes como funções $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ . Linha do meio: interpretação de matrizes como funções $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R$ .



Assim, trabalharei com matrizes definidas positivas, que são uma generalização de números positivos. Além disso, especificamente no meu caso, as matrizes também serão simétricas! É curioso que, muitas vezes, quando as pessoas falam sobre certeza positiva, elas também significam simetria, que pode ser indiretamente explicada pela seguinte observação (opcional para a compreensão do texto subsequente).

Digressão lírica na simetria de matrizes de formas quadráticas

Vamos olhar para a forma quadrática $$$x ^ \ top M x$ para uma matriz arbitrária $$$M$ ; então para $$$M$ adicione e subtraia imediatamente metade de sua versão transposta:

$$

$$M = \ underbrace {\ frac {1} {2} (M + M ^ \ top)} _ {: = M_s} + \ underbrace {\ frac {1} {2} (MM ^ \ top)} _ { : = M_a} = M_s + M_a$$

Matrix $$$M_s$ simétrico: $$$M_s ^ \ top = M_s$ ; matriz $$$M_a$ antissimétrico: $$$M_a ^ \ top = -M_a$ . Um fato notável é que, para qualquer matriz antissimétrica, a forma quadrática correspondente é identicamente igual a zero. Isto segue da seguinte observação:

$$

$$q = x ^ \ top M_a x = (x ^ \ top M_a ^ \ top x) ^ \ top = - (x ^ \ top M_a x) ^ \ top = -q$$

Ou seja, a forma quadrática $$$x ^ \ top M_a x$ simultaneamente igual $$$q$ e $$$-q$ , o que é possível apenas quando $$$q \ equiv. 0$ . Desse fato, segue-se que para uma matriz arbitrária $$$M$ forma quadrática correspondente $$$x ^ \ top M x$ pode ser expresso através de uma matriz simétrica $$$M_s$ :

$$

$$x ^ \ top M x = x ^ \ top (M_s + M_a) x = x ^ \ top M_s x + x ^ \ top M_a x = x ^ \ top M_s x.$$

Estamos procurando um mínimo de uma função quadrática

Voltemos brevemente ao mundo unidimensional; Eu quero encontrar um mínimo de função $$$f (x) = ax ^ 2 - 2bx$ . Número $$$a$ positivamente, portanto, existe um mínimo; para encontrá-lo, igualamos a zero a derivada correspondente: $$$\ frac {d} {dx} f (x) = 0$ . Diferenciar a função quadrática unidimensional do trabalho não é: $$$\ frac {d} {dx} f (x) = 2ax - 2b = 0$ ; então nosso problema se resume a resolver a equação $$$ax-b = 0$ , onde, através de esforços terríveis, obtemos uma solução $$$x ^ * = b / a$ . A figura a seguir ilustra a equivalência de dois problemas: solução $$$x ^ *$ equações $$$ax-b = 0$ coincide com a solução da equação $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ .



Costumo ao fato de que nosso objetivo global é minimizar as funções quadráticas, mas estamos falando de mínimos quadrados. Mas, ao mesmo tempo, o que realmente sabemos fazer bem é resolver equações lineares (e sistemas de equações lineares). E é muito legal que um seja equivalente ao outro!

A única coisa que resta para nós é garantir que essa equivalência no mundo unidimensional se estenda ao caso $$$n$ variáveis. Para verificar isso, primeiro provamos três teoremas.

Três teoremas, ou diferenciam expressões matriciais

O primeiro teorema afirma que as matrizes $$ invariantes em relação à transposição:

Teorema 1

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

A prova é tão complicada que eu tenho que omiti-la por uma questão de brevidade, mas tente encontrá-la.

O segundo teorema nos permite diferenciar funções lineares. No caso de uma função real de uma variável, sabemos que $$$\ frac {d} {dx} (bx) = b$ mas o que acontece no caso de uma função real $$$n$ variáveis?

Teorema 2

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

Ou seja, sem surpresas, apenas uma gravação matricial do mesmo resultado escolar. A prova é extremamente direta, basta escrever a definição do gradiente:

$$

$$\ nabla (b ^ \ top x) = \ begin {bmatrix} \ frac {\ parcial (b ^ \ top x)} {\ parcial x_1} \\ \ vdots \\ \ frac {\ parcial (b ^ \ top x)} {\ x_n parcial} \ end {bmatrix} = \ begin {bmatrix} \ frac {\ parcial (b_1 x_1 + \ pontos + b_n x_n)} {\ x_1 parcial} \\ \ vdots \\ \ frac {\ parcial (b_1 x_1 + \ pontos + b_n x_n)} {\ parcial x_n} \ end {bmatrix} = \ begin {bmatrix} b_1 \\ \ vdots \\ b_n \ end {bmatrix} = b$$

Aplicando o primeiro teorema $$$b ^ \ top x = x ^ \ top b$ , concluímos a prova.

Agora passamos para formas quadráticas. Sabemos que, no caso de uma função real de uma variável $$$\ frac {d} {dx} (ax ^ 2) = 2ax$ e o que acontecerá no caso de uma forma quadrática?

Teorema 3

$$$\ nabla (x ^ \ top A x) = (A + A ^ \ top) x$

A propósito, observe que se a matriz $$$A$ simétrica, o teorema diz que $$$\ nabla (x ^ \ top A x) = 2Ax$ .

Essa prova também é simples, basta escrever a forma quadrática como uma soma dupla:

$$

$$x ^ \ top A x = \ soma \ limites_i \ soma \ limites_j a_ {ij} x_i x_j$$

E então vamos ver qual é a derivada parcial dessa soma dupla em relação à variável $$$x_i$ :
\ begin {align *}
\ frac {\ parcial (x ^ \ top A x)} {\ parcial x_i}
& = \ frac {\ parcial} {\ parcial x_i} \ left (\ sum \ limits_ {k_1} \ sum \ limits_ {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} \ right) = \\
& = \ frac {\ parcial} {\ parcial x_i} \ esquerda (
\ underbrace {\ sum \ limits_ {k_1 \ neq i} \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ {k_1 \ neq i, k_2 \ neq i} + \ sustentar {\ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i, k_2 \ neq i} +
\ underbrace {\ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i, k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i, k_2 = i} \ right) = \\
& = \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} + 2 a_ {ii} x_i = \\
& = \ sum \ limits_ {k_2} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1} a_ {k_1 i} x_ {k_1} = \\
& = \ sum \ limits_ {j} (a_ {ij} + a_ {ji}) x_j \\
\ end {align *}
Dividi a soma dupla em quatro casos, destacados por chaves. Cada um desses quatro casos se diferencia trivialmente. Resta fazer a última ação, coletar as derivadas parciais no vetor gradiente:

$$

$$\ nabla (x ^ \ top A x) = \ begin {bmatrix} \ frac {\ parcial (x ^ \ top Axe)} {\ parcial x_1} \\ \ vdots \\ \ frac {\ parcial (x ^ \ topo A x)} {\ x_n parcial} \ end {bmatrix} = \ begin {bmatrix} \ sum \ limits_ {j} (a_ {1j} + a_ {j1}) x_j \\ \ vdots \\ \ sum \ limits_ {j} (a_ {nj} + a_ {jn}) x_j \ end {bmatrix} = (A + A ^ \ top) x$$

O mínimo da função quadrática e a solução do sistema linear

Não vamos esquecer a direção da viagem. Vimos que com um número positivo $$$a$ no caso de funções reais de uma variável, resolva a equação $$$ax = b$ ou minimizar a função quadrática $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ São uma e a mesma coisa.

Queremos mostrar a conexão correspondente no caso de uma matriz definida positiva simétrica $$$A$ .
Então, queremos encontrar o mínimo da função quadrática

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n} (x ^ \ top A x - 2b ^ \ top x).$$

Exatamente como na escola, equiparamos a derivada a zero:

$$

$$\ nabla (x ^ \ top A x - 2b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}.$$

O operador Hamilton é linear, para que possamos reescrever nossa equação da seguinte forma:

$$

$$\ nabla (x ^ \ top A x) - 2 \ nabla (b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Agora aplicamos o segundo e o terceiro teoremas de diferenciação:

$$

$$(A + A ^ \ top) x - 2b = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Lembre-se que $$$A$ simétrica, e dividir a equação em duas, obtemos o sistema de equações lineares de que precisamos:

$$

$$Ax = b$$

Viva, passando de uma variável para muitas, não perdemos nada e podemos minimizar efetivamente as funções quadráticas!

Passamos para os mínimos quadrados

Finalmente, podemos avançar para o conteúdo principal desta palestra. Imagine que temos dois pontos em um avião $$$(x_1, y_1)$ e $$$(x_2, y_2)$ , e queremos encontrar a equação de uma linha que passa por esses dois pontos. A equação da linha pode ser escrita como $$$y = \ alpha x + \ beta$ , ou seja, nossa tarefa é encontrar os coeficientes $$$\ alpha$ e $$$\ beta$ . Este exercício é para a sétima e oitava série da escola, escrevemos o sistema de equações:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ end {split} \ right.$$

Temos duas equações com duas incógnitas ( $$$\ alpha$ e $$$\ beta$ ), o resto é conhecido.

No caso geral, existe uma solução e é única. Por conveniência, reescrevemos o mesmo sistema em forma de matriz:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \ end {bmatrix}} _ {: = A} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \ end {bmatrix}} _ {: = b}$$

Obtemos uma equação do tipo $$$Ax = b$ que é resolvido trivialmente $$$x ^ * = A ^ {- 1} b$ .

Agora imagine que temos três pontos através dos quais precisamos desenhar uma linha reta:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ alpha x_3 + \ beta & = y_3 \\ \ end {divisão} \ right .$$

Em forma de matriz, este sistema é escrito da seguinte maneira:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}} _ {: = A \, (3 \ times 2)} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x \, (2 \ times 1)} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}} _ { : = b \, (3 \ vezes 1)}$$

Agora nós temos uma matriz $$$A$ retangular, e simplesmente não existe reverso! Isso é completamente normal, pois temos apenas duas variáveis ​​e três equações e, no caso geral, esse sistema não tem solução. Esta é uma situação completamente normal no mundo real, quando os pontos são dados de medições ruidosas e precisamos encontrar os parâmetros $$$\ alpha$ e $$$\ beta$ que melhor aproximam os dados de medição. Já consideramos esse exemplo na primeira aula, quando calibrado em aço. Mas então nossa solução foi puramente algébrica e muito complicada. Vamos tentar uma maneira mais intuitiva.

Nosso sistema pode ser escrito da seguinte maneira:

$$

$$\ alpha \ underbrace {\ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ {: = \ vec {i}} + \ beta \ underbrace {\ begin {bmatrix} 1 \\ 1 \ \ 1 \ end {bmatrix}} _ {: = \ vec {j}} = \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}$$

Ou, mais brevemente,

$$

$$\ alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}.$$

Vetores $$$\ v i$ , $$$\ vec j$ e $$$\ vec b$ conhecido, precisa encontrar escalares $$$\ alpha$ e $$$\ beta$ .
Combinação obviamente linear $$$\ alpha \ vec {i} + \ beta \ vec {j}$ gera um avião e se o vetor $$$\ vec b$ não se encontra neste plano, então não há solução exata; no entanto, estamos procurando uma solução aproximada.

Vamos definir o erro de decisão como $$$\ vec {e} (\ alpha, \ beta): = \ alpha \ vec {i} + \ beta \ vec {j} - \ vec b$ . Nosso objetivo é encontrar esses valores de parâmetro $$$\ alpha$ e $$$\ beta$ que minimizam o comprimento do vetor $$$\ vec {e} (\ alpha, \ beta)$ . Em outras palavras, o problema está escrito como $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ .
Aqui está uma ilustração:.



Tendo dado vetores $$$\ v i$ , $$$\ vec j$ e $$$\ vec b$ , tentamos minimizar o comprimento do vetor de erro $$$\ vec e$ . Obviamente, seu comprimento é minimizado se for perpendicular ao plano esticado sobre os vetores $$$\ v i$ e $$$\ vec j$ .

Mas espere, onde estão os mínimos quadrados? Agora eles serão. Função de extração de raiz $$$\ sqrt {\ cdot}$ monótono, portanto $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ = $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ !

É bastante óbvio que o comprimento do vetor de erro é minimizado se for perpendicular ao plano esticado sobre os vetores $$$\ v i$ e $$$\ vec j$ , que pode ser escrito equiparando a zero os produtos escalares correspondentes:

$$

$$\ left \ {\ begin {split} \ vec {i} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \\ \ vec {j} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \ end {split} \ right.$$

Em forma de matriz, esse mesmo sistema pode ser escrito como

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ alpha \ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix} + \ beta \ begin {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

ou então

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix} \ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

Mas não vamos parar por aí, pois o registro pode ser reduzido ainda mais:

$$

$$A ^ \ top (Ax - b) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix}$$

E a transformação mais recente:

$$

$$A ^ \ top Ax = A ^ \ top b.$$

Vamos calcular as dimensões. Matrix $$$A$ tem tamanho $$$3 \ vezes 2$ portanto $$$A ^ \ top A$ tem tamanho $$$2 \ vezes 2$ . Matrix $$$b$ tem tamanho $$ mas vector $$$A ^ \ top b$ tem tamanho $$$2 \ vezes 1$ . Ou seja, no caso geral, a matriz $$$A ^ \ top A$ reversível! Além disso, $$$A ^ \ top A$ Tem algumas boas propriedades.

Teorema 4

$$$A ^ \ top A$ simétrico.

Isso não é nada difícil de mostrar:

$$

$$(A ^ \ top A) ^ \ top = A ^ \ top (A ^ \ top) ^ \ top = A ^ \ top A.$$

Teorema 5

$$$A ^ \ top A$ positivamente semi-definido: $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geq 0.$

Isto decorre do fato de que $$$x ^ \ top A ^ \ top A x = (A x) ^ \ top A x> 0$ .

Também $$$A ^ \ top A$ positivo definitivo se $$$A$ possui colunas linearmente independentes (classificação $$$A$ igual ao número de variáveis ​​no sistema).

No total, para um sistema com duas incógnitas, provamos que a minimização de uma função quadrática $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ equivalente a resolver um sistema de equações lineares $$$A ^ \ top A x = A ^ \ top b$ . Obviamente, todo esse raciocínio se aplica a qualquer outro número de variáveis, mas vamos escrever tudo de forma compacta novamente com um cálculo algébrico simples. Começamos com o problema dos mínimos quadrados, chegamos à minimização da função quadrática da forma familiar e daí concluímos que é equivalente a resolver um sistema de equações lineares. Então vamos lá:

$$

$$\ begin {split} \ mathrm {argmin} \ | Ax - b \ | ^ 2 & = \ mathrm {argmin} (Ax-b) ^ \ top (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top - b ^ \ top) (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - b ^ \ top Ax - x ^ \ top A ^ \ top b + \ underbrace {b ^ \ top b} _ {\ rm const}) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - 2b ^ \ top Ax) = \\ & = \ mathrm {argmin} ( x ^ \ top \ underbrace {(A ^ \ top A)} _ {: = A '} x - 2 \ underbrace {(A ^ \ top b)} _ {: = b'} \ fantasma {} ^ \ top x) \ end {split}$$

Então o problema dos mínimos quadrados $$$\ mathrm {argmin} \ | Machado - b \ | ^ 2$ equivalente a minimizar uma função quadrática $$$\ mathrm {argmin} (x ^ \ top A 'x - 2b' ^ \ top x)$ com (no caso geral) uma matriz definida positiva simétrica $$$A '$ , que, por sua vez, é equivalente a resolver um sistema de equações lineares $$$A'x = b '$ . Uff. A teoria acabou.

Vamos seguir praticando

Exemplo Um, Unidimensional

Vamos relembrar um exemplo de um artigo anterior :

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

Temos uma matriz x regular de 32 elementos, inicializada da seguinte maneira:



E então executaremos o seguinte procedimento mil vezes: para cada célula x [i], escrevemos nela o valor médio das células vizinhas: x [i] = (x [i-1] + x [i + 1]) / 2. A única exceção: não reescreveremos os elementos da matriz com os números 0, 18 e 31. É assim que a evolução da matriz se parece nas primeiras cento e cinquenta iterações:



Como descobrimos em um artigo anterior , verifica-se que nosso megacódigo de código python de quatro linhas resolve o seguinte sistema de equações lineares pelo método de Gauss-Seidel:



Eles descobriram, mas de onde veio esse sistema? Que tipo de magia? Vamos discordar por um segundo e tentar resolver um sistema ligeiramente diferente. Eu ainda tenho 32 variáveis, mas agora quero que todas sejam iguais. Não é difícil escrever, basta escrever um sistema de equações que declara que todos os elementos vizinhos são iguais em pares:



O código Python acima, em princípio, não toca nos valores de três variáveis: x0, x18, x31, então vamos transferi-los para o lado direito do sistema de equações, ou seja, excluir do conjunto de incógnitas:



Eu fixo o valor inicial x0 = 1, a primeira equação diz x1 = x0 = 1, a segunda equação diz x2 = x1 = x0 = 1 e assim por diante, até chegarmos à equação 1 = x0 = x17 = x18 = 2 Oh Mas este sistema não tem solução: ((

E não se preocupe, somos programadores! Vamos chamar os mínimos quadrados para obter ajuda! Nosso sistema insolúvel pode ser escrito em forma de matriz $$$Ax = b$ ; para resolver nosso sistema aproximadamente, basta resolver o sistema $$$A^\top Ax=A^\top b$ .E então acontece que este é exatamente o sistema de equações um-em-um do artigo anterior!

Intuitivamente, pode-se imaginar o processo de criação de uma matriz do sistema da seguinte maneira: conectamos os valores às molas que queremos alcançar a igualdade. Por exemplo, no nosso caso, queremos$$$x_i$ era igual $$$x_{i+1}$ , então adicionamos a equação $$$x_i - x_{i+1}=0$pendurando entre esses valores uma mola que os unirá. Mas como os valores de x0, x18 e x31 são firmemente fixos, não resta mais valores livres para esticar as molas uniformemente, produzindo (neste caso) uma solução linear por partes.

Vamos escrever um programa que resolva esse sistema de equações. No último artigo, vimos que o método Gauss-Seidel é muito simples em programação, mas possui uma convergência muito lenta; portanto, seria melhor usar solucionadores reais de sistemas de equações lineares. No caso mais simples, para o nosso exemplo unidimensional, o código pode ser algo como isto:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

Este código produz uma lista x de 32 elementos nos quais a solução está armazenada. Estamos construindo uma matriz$$$A$ construção de vetor $$$b$ temos um vetor com uma solução $$$x = (A^\top A)^{-1}A^\top b$e então inserimos nossos valores fixos x0 = 1, x18 = 2 e x31 = 1 nesse vetor.

Esse código faz o trabalho necessário, mas é bastante desagradável transferir os valores de variáveis ​​fixas para o lado direito. É possível trapacear? Você pode! Vejamos o seguinte código:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

Do ponto de vista do programador, é muito melhor, o vetor x é obtido imediatamente da dimensão requerida e as matrizes A e b são preenchidas com muito mais facilidade. Mas qual é o truque? Vamos escrever o sistema de equações que resolvemos:



Observe atentamente as três últimas equações:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1

Seria mais fácil escrevê-las da seguinte maneira?
x0 = 1
x18 = 2
x31 = 1

Não, não é mais fácil. Como eu já disse, cada equação trava molas, neste caso, a mola entre x0 e o valor 1, a mola entre x18 e o valor 2 e, finalmente, a variável x31 também será atraída para a unidade.

Mas o coeficiente de 100 existe por uma razão. Lembramos que este sistema simplesmente não pode ser resolvido, o resolvemos no sentido de mínimos quadrados, minimizando a função quadrática correspondente. Multiplicando por 100 cada um dos coeficientes das três últimas equações, introduzimos uma penalidade por desviar x0, x18 e x32 dos valores desejados, dez mil vezes (100 ^ 2) excedendo a penalidade por desviar da igualdade$$$x_i = x_{i+1}$ .Grosso modo, as fontes nas três últimas equações são dez mil vezes mais difíceis do que em todas as outras. Esse método de penalidade quadrática é uma ferramenta muito conveniente para a introdução de restrições; é muito mais simples (embora não sem desvantagens) do que reduzir um conjunto de variáveis.

Exemplo dois, tridimensional

Vamos para algo mais interessante do que suavizar os elementos de uma matriz unidimensional! Para começar, faremos exatamente o mesmo, mas com dados mais interessantes e com ferramentas reais. Desejo pegar uma superfície tridimensional, corrigir sua borda e suavizar o restante da superfície o máximo possível:



O código está disponível aqui , mas apenas no caso de fornecer uma lista completa do arquivo principal:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

Eu escrevi o analisador mais simples de arquivos .obj de frente de onda, para que o modelo seja carregado em uma linha. Como solucionador, usarei o OpenNL, é um solucionador muito poderoso para problemas de mínimos quadrados com matrizes esparsas. Observe que as dimensões das matrizes podem ser gigantescas: por exemplo, se queremos obter uma imagem em preto e branco com um tamanho de 1000 x 1000 pixels, a matriz$$$A^\top A$teremos um tamanho de um milhão por milhão! No entanto, na prática, na maioria das vezes a grande maioria dos elementos dessa matriz é zero, então nem tudo é tão assustador, mas você ainda precisa usar solucionadores especiais.

Então, vamos olhar o código. Para começar, anuncio ao solucionador o que quero fazer:

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

Eu quero ter uma matriz $$$A^\top A$tamanho (número de vértices) x (número de vértices). Atenção, damos ao solucionador uma matriz$$$A$ e $$$A^\top A$ele mesmo construirá, o que é muito conveniente! Além disso, preste atenção ao fato de eu resolver não um sistema de equações, mas três em série para x, ye z (menti que o problema é tridimensional, ainda é unidimensional!)

E então declaro linha por linha da nossa matriz. Para começar, corrijo os vértices que estão na borda da superfície:

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

Você pode ver que estou usando uma penalidade quadrada de 100 ^ 2 para corrigir os vértices da aresta.

Bem, então para cada par de vértices adjacentes eu penduro uma mola de rigidez 1 entre eles:

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

Executamos o código e vemos como o rosto suavizou a superfície do filme de sabão em um fio curvo. Acabamos de resolver o problema de Dirichlet, obtendo uma superfície de área mínima.

Melhoramos as características

Vamos transformar nosso rosto em uma máscara grotesca:



no artigo anterior, eu já mostrei como fazer isso no joelho, aqui eu dou um código real que usa o solucionador de mínimos quadrados:

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

O código completo está disponível aqui . Como ele trabalha? Como no exemplo anterior, começo fixando os vértices da aresta. Então, para cada aresta, eu (silenciosamente, com um coeficiente de 0,2) digo que seria bom se tivesse exatamente a mesma forma da superfície original:

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

Se você não fizer mais nada e resolver o problema exatamente como é, devemos obter exatamente o que estava na saída na saída: a borda de saída é igual à borda de entrada, mais as diferenças na saída são iguais às diferenças na entrada.

Mas não vamos parar por aí!

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

Eu adiciono mais equações ao nosso sistema. Para cada vértice, conto a curvatura da superfície em torno dela na superfície de entrada e multiplico por dois anos e meio, ou seja, a superfície de saída deve ter uma grande curvatura em todos os lugares.

Então chamamos nosso solucionador e obtemos uma boa caricatura.

Último exemplo para hoje

Até o momento, não vimos um único exemplo novo, tudo já foi mostrado no artigo anterior. Vamos tentar fazer algo menos trivial do que a suavização mais simples, que pode ser facilmente obtida sem o uso de nenhum solucionador. O código está disponível aqui , mas deixe-me fornecer uma listagem:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

Ainda estamos trabalhando na mesma superfície de antes; chamamos a função snap () para cada triângulo. Essa função diz qual eixo do sistema de coordenadas está mais próximo do normal desse triângulo. Ou seja, queremos saber que esse triângulo é mais provável vertical ou horizontal. Bem, então queremos mudar a geometria da nossa superfície para que o que é mais próximo da horizontal se torne ainda mais próximo! A parte esquerda desta imagem mostra o resultado da função snap ():



Então, pintamos nossa superfície em três cores, correspondendo aos três eixos do sistema de coordenadas. Bem, então, para cada extremidade do nosso sistema, adicionamos as seguintes equações:

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

Ou seja, instruímos cada aresta da superfície de saída a se parecer com a aresta correspondente da superfície de entrada, rigidez da mola 1. E então, se permitirmos, por exemplo, a dimensão x, e a aresta deve ser vertical, simplesmente dizemos que um vértice é igual ao outro com rigidez da mola 2:

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

Bem, aqui está o resultado do nosso programa: Uma



pergunta perfeitamente razoável: ídolos da Ilha de Páscoa, é claro que isso é legal, mas o que a geologia tem a ver com isso? Existem exemplos de problemas reais?

Sim claro. Vamos dar uma seção da crosta terrestre:



para geólogos, camadas de rochas diferentes são muito importantes, os limites (horizontes) entre os quais são mostrados em verde e as falhas geológicas que são mostradas em vermelho. Temos na entrada uma grade de triângulos (tetraedros em 3D) da área que nos interessa, mas quads (hexaedros em 3D) são necessários para modelar certos processos. Deformamos nosso modelo para que as falhas se tornem verticais e os horizontes (surpresa) horizontais:



Depois, pegamos uma grade regular de quadrados, cortamos nosso domínio em quadrados uniformes e aplicamos a transformação inversa a eles, obtendo a grade necessária de quadriláteros.

Conclusão

Os métodos dos mínimos quadrados são uma poderosa ferramenta de processamento de dados e são usados ​​muito mais amplamente que as estatísticas nas colunas do Excel. Essas possibilidades nos são abertas devido ao fato de que minimizar uma função quadrática e resolver um sistema de equações lineares são uma e a mesma coisa, e nós (humanidade) aprendemos a resolver equações lineares muito, muito bem, até tamanhos completamente desumanos com bilhões de variáveis.

No entanto, há momentos em que podemos não ter modelos lineares suficientes. E aqui, por exemplo, redes neurais podem ajudar. No próximo artigo, tentarei mostrar que o OLS com rejeição de emissões é equivalente a uma das formulações de redes neurais. Fique na linha!