RayTracing compreensível em 256 linhas de C ++
Este é outro capítulo do meu breve curso de palestras sobre computação gráfica . Desta vez, estamos falando sobre o traçado de raios. Como sempre, tento evitar bibliotecas de terceiros, pois acredito que isso faz os alunos verificarem o que está acontecendo sob o capô. Verifique também o projeto tinykaboom .
Existem muitos artigos sobre raytracing na web; no entanto, o problema é que quase todos mostram software acabado que pode ser bastante difícil de entender. Tomemos, por exemplo, o famoso desafio do ray tracer de cartões de negócios . Produz programas muito impressionantes, mas é muito difícil entender como isso funciona. Em vez de mostrar que eu posso fazer renderizações, quero lhe contar em detalhes como você pode fazer isso sozinho.
Nota: Não faz sentido olhar apenas para o meu código, nem ler este artigo com uma xícara de chá na mão. Este artigo foi projetado para você pegar o teclado e implementar seu próprio mecanismo de renderização. Certamente será melhor que o meu. No mínimo, mude a linguagem de programação!
Portanto, o objetivo de hoje é aprender a renderizar essas imagens:

Etapa 1: gravar uma imagem no disco
Não quero me preocupar com gerenciadores de janelas, processamento de mouse / teclado e coisas assim. O resultado do nosso programa será uma imagem simples salva em disco. Portanto, a primeira coisa que precisamos fazer é salvar a imagem em disco. Aqui você pode encontrar o código que nos permite fazer isso. Deixe-me listar o arquivo principal:
#include <limits> #include <cmath> #include <iostream> #include <fstream> #include <vector> #include "geometry.h" void render() { const int width = 1024; const int height = 768; std::vector<Vec3f> framebuffer(width*height); for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } } std::ofstream ofs; // save the framebuffer to file ofs.open("./out.ppm"); ofs << "P6\n" << width << " " << height << "\n255\n"; for (size_t i = 0; i < height*width; ++i) { for (size_t j = 0; j<3; j++) { ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j]))); } } ofs.close(); } int main() { render(); return 0; }
Somente render () é chamado na função principal e nada mais. O que há dentro da função render ()? Antes de tudo, defino o framebuffer como uma matriz unidimensional de valores Vec3f, esses são vetores tridimensionais simples que nos fornecem valores (r, g, b) para cada pixel. A classe de vetores reside no arquivo geometry.h, não vou descrevê-lo aqui: é realmente uma manipulação trivial de vetores bidimensionais e tridimensionais (adição, subtração, atribuição, multiplicação por um produto escalar e escalar).
Eu salvo a imagem no formato ppm . É a maneira mais fácil de salvar imagens, embora nem sempre seja a maneira mais conveniente de visualizá-las mais. Se você deseja salvar em outros formatos, recomendo que você vincule uma biblioteca de terceiros, como stb . Esta é uma ótima biblioteca: você só precisa incluir um arquivo de cabeçalho stb_image_write.h no projeto e permitirá salvar imagens nos formatos mais populares.
Aviso: meu código está cheio de bugs, eu os corrigo no upstream, mas as confirmações mais antigas são afetadas. Verifique este problema .
Portanto, o objetivo desta etapa é garantir que: a) crie uma imagem na memória + atribua cores diferentes eb) salve o resultado no disco. Então você pode vê-lo em um software de terceiros. Aqui está o resultado:

Etapa 2, crucial: rastreamento de raios
Este é o passo mais importante e difícil de toda a cadeia. Quero definir uma esfera no meu código e desenhá-la sem ser obcecada por materiais ou iluminação. É assim que nosso resultado deve ser:

Por uma questão de conveniência, tenho um commit por etapa no meu repositório; O Github facilita muito a visualização das alterações feitas. Aqui, por exemplo , o que foi alterado pelo segundo commit.
Para começar, o que precisamos para representar a esfera na memória do computador? Quatro números são suficientes: um vetor tridimensional para o centro da esfera e um escalar que descreve o raio:
struct Sphere { Vec3f center; float radius; Sphere(const Vec3f &c, const float &r) : center(c), radius(r) {} bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const { Vec3f L = center - orig; float tca = L*dir; float d2 = L*L - tca*tca; if (d2 > radius*radius) return false; float thc = sqrtf(radius*radius - d2); t0 = tca - thc; float t1 = tca + thc; if (t0 < 0) t0 = t1; if (t0 < 0) return false; return true; } };
A única coisa não trivial neste código é uma função que permite verificar se um determinado raio (originário de orig na direção de dir) cruza com a nossa esfera. Uma descrição detalhada do algoritmo para a interseção raio-esfera pode ser encontrada aqui , eu recomendo que você faça isso e verifique meu código.
Como funciona o traçado de raios? É bem simples. Na primeira etapa, apenas preenchemos a imagem com um gradiente de cores:
for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } }
Agora, para cada pixel, formaremos um raio vindo da origem e passando por nosso pixel e, em seguida, verificar se esse raio se cruza com a esfera:

Se não houver interseção com a esfera, desenhamos o pixel com color1, caso contrário com color2:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { float sphere_dist = std::numeric_limits<float>::max(); if (!sphere.ray_intersect(orig, dir, sphere_dist)) { return Vec3f(0.2, 0.7, 0.8);
Neste ponto, recomendo que você pegue um lápis e verifique no papel todos os cálculos (a interseção raio-esfera e a varredura da imagem com os raios). Por precaução, nossa câmera é determinada pelas seguintes coisas:
- largura da imagem
- altura da imagem
- ângulo do campo de visão
- localização da câmera, Vec3f (0.0.0)
- visualizar a direção, ao longo do eixo z, na direção do infinito negativo
Deixe-me ilustrar como calculamos a direção inicial do raio para traçar. No loop principal, temos esta fórmula:
float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height; float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);
De onde vem? Bem simples. Nossa câmera é colocada na origem e está voltada para a direção -z. Deixe-me ilustrar as coisas: esta imagem mostra a câmera de cima, o eixo y aponta para fora da tela:
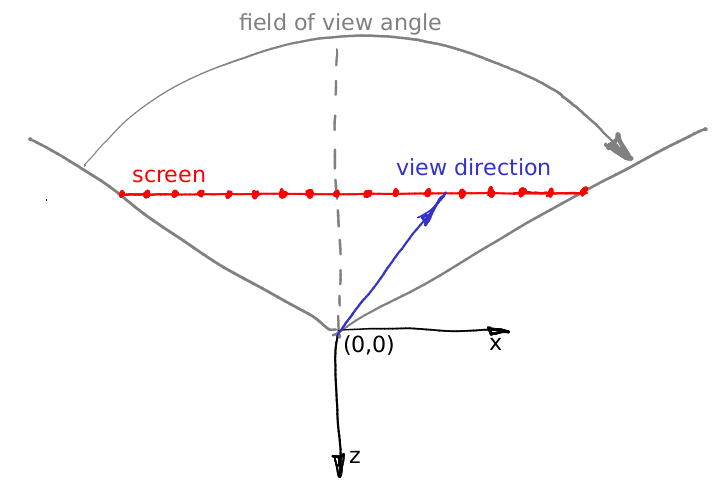
Como eu disse, a câmera é colocada na origem e a cena é projetada na tela que fica no plano z = -1. O campo de visão especifica qual setor do espaço será visível na tela. Em nossa imagem, a tela tem 16 pixels de largura; você pode calcular seu comprimento em coordenadas mundiais? É bem simples: vamos nos concentrar no triângulo formado pelas linhas tracejada vermelha, cinza e cinza. É fácil ver que o bronzeado (campo de visão / 2) = (largura da tela) 0,5 / (distância da câmera da tela). Colocamos a tela a uma distância de 1 da câmera, assim (largura da tela) = 2 tan (campo de visão / 2).
Agora, digamos que queremos converter um vetor no centro do 12º pixel da tela, ou seja, queremos calcular o vetor azul. Como podemos fazer isso? Qual é a distância da esquerda da tela até a ponta do vetor azul? Primeiro de tudo, são 12 + 0,5 pixels. Sabemos que 16 pixels da tela correspondem a 2 unidades mundiais tan (fov / 2). Assim, a ponta do vetor está localizada em (12 + 0,5) / 16 2 tan (fov / 2) unidades mundiais da borda esquerda ou à distância de (12 + 0,5) 2/16 * tan (fov / 2) - tan (fov / 2) a partir da interseção entre a tela e o eixo -z. Adicione a proporção da tela aos cálculos e você encontrará exatamente as fórmulas para a direção do raio.
Etapa 3: adicione mais esferas
A parte mais difícil acabou e agora nosso caminho está claro. Se soubermos desenhar uma esfera, não levaremos muito tempo para adicionar mais algumas. Verifique as alterações no código e esta é a imagem resultante:

Etapa 4: iluminação
A imagem é perfeita em todos os aspectos, exceto pela falta de luz. Ao longo do restante do artigo, falaremos sobre iluminação. Vamos adicionar algumas fontes de luz pontuais:
struct Light { Light(const Vec3f &p, const float &i) : position(p), intensity(i) {} Vec3f position; float intensity; };
A computação da iluminação global real é uma tarefa muito, muito difícil; portanto, como todos os outros, enganaremos os olhos desenhando resultados completamente não físicos, mas visualmente plausíveis. Para começar: por que está frio no inverno e quente no verão? Porque o aquecimento da superfície da Terra depende do ângulo de incidência dos raios solares. Quanto mais alto o sol nasce acima do horizonte, mais brilhante é a superfície. Por outro lado, quanto mais baixo estiver acima do horizonte, mais escuro será. E depois que o sol se põe no horizonte, os fótons nem chegam a nós.
De volta às nossas esferas: emitimos um raio da câmera (sem relação com fótons!). Ele para em uma esfera. Como sabemos a intensidade da iluminação do ponto de interseção? De fato, basta verificar o ângulo entre um vetor normal neste ponto e o vetor que descreve uma direção da luz. Quanto menor o ângulo, melhor a superfície é iluminada. Lembre-se de que o produto escalar entre dois vetores aeb é igual ao produto das normas dos vetores vezes o cosseno do ângulo entre os vetores: a * b = | a | | b | cos (alfa (a, b)). Se pegarmos vetores de comprimento unitário, o produto escalar nos dará a intensidade da iluminação da superfície.
Assim, na função cast_ray, em vez de uma cor constante, retornaremos a cor levando em consideração as fontes de luz:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { [...] float diffuse_light_intensity = 0; for (size_t i=0; i<lights.size(); i++) { Vec3f light_dir = (lights[i].position - point).normalize(); diffuse_light_intensity += lights[i].intensity * std::max(0.f, light_dir*N); } return material.diffuse_color * diffuse_light_intensity; }
As modificações feitas na etapa anterior estão disponíveis aqui , e aqui está o resultado:

Etapa 5: iluminação especular
O truque do produto com pontos fornece uma boa aproximação da iluminação de superfícies mate, na literatura é chamada de iluminação difusa. O que devemos fazer se queremos desenhar superfícies brilhantes? Quero tirar uma foto assim:

Verifique quantas modificações foram necessárias. Em resumo, quanto mais brilhante a luz nas superfícies brilhantes, menor o ângulo entre a direção da vista e a direção da luz refletida .
Esse truque com iluminação de superfícies foscas e brilhantes é conhecido como modelo de reflexão Phong . O wiki tem uma descrição bastante detalhada desse modelo de iluminação. Pode ser bom lê-lo lado a lado com o código fonte. Aqui está a imagem principal para entender a mágica:

Etapa 6: sombras
Por que temos a luz, mas sem sombras? Não está tudo bem! Quero esta foto:

Apenas seis linhas de código nos permitem alcançar isso: ao desenhar cada ponto, apenas garantimos que o segmento entre o ponto atual e a fonte de luz não cruze os objetos de nossa cena. Se houver uma interseção, pularemos a fonte de luz atual. Há apenas uma pequena sutileza: eu perturbo o ponto movendo-o na direção normal:
Vec3f shadow_orig = light_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Por que isso? Só que nosso ponto está na superfície do objeto e (exceto na questão de erros numéricos) qualquer raio desse ponto cruzará o próprio objeto.
Etapa 7: reflexões
É incrível, mas para adicionar reflexões à nossa renderização, precisamos apenas adicionar três linhas de código:
Vec3f reflect_dir = reflect(dir, N).normalize(); Vec3f reflect_orig = reflect_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Veja você mesmo: ao cruzar a esfera, apenas calculamos o raio refletido (com a ajuda da mesma função que usamos para realces especulares!) E chamamos recursivamente a função cast_ray na direção do raio refletido. Certifique-se de jogar com a profundidade da recursão , defino-a como 4, tente valores diferentes, começando por 0, o que mudará na imagem? Aqui está o meu resultado com reflexões e uma profundidade de recursão de 4:

Etapa 8: refrações
Se sabemos fazer reflexões, as refrações são fáceis . Precisamos adicionar uma função para calcular o raio refratado ( usando a lei de Snell ) e mais três linhas de código em nossa função recursiva cast_ray. Aqui está o resultado, onde a bola mais próxima é "feita de vidro", ela reflete e refrata a luz ao mesmo tempo:

Steo 9: além das esferas
Até este momento, renderizamos apenas esferas porque é um dos objetos matemáticos não triviais mais simples. Vamos adicionar um avião. O tabuleiro de xadrez é uma escolha clássica. Para esse fim, basta adicionar uma dúzia de linhas .
E aqui está o resultado:

Como prometido, o código tem 256 linhas de código, verifique você mesmo !
Etapa 10: tarefa de casa
Percorremos um longo caminho: aprendemos como adicionar objetos a uma cena, como calcular uma iluminação bastante complicada. Deixe-me deixar duas tarefas para você como lição de casa. Absolutamente todo o trabalho preparatório já foi realizado no ramo homework_assignment . Cada tarefa exigirá dez linhas de tops de código.
Tarefa 1: mapa do ambiente
No momento, se o raio não cruzar nenhum objeto, basta definir o pixel com a cor de fundo constante. E por que, na verdade, é constante? Vamos tirar uma foto esférica (arquivo envmap.jpg ) e usá-la como pano de fundo! Para facilitar a vida, vinculei nosso projeto à biblioteca stb para a conveniência de trabalhar com o formato jpg. Deveria nos dar uma imagem assim:

Tarefa 2: Quack-Quack!
Podemos renderizar esferas e planos (veja o tabuleiro de damas). Então, vamos desenhar malhas triangulares! Eu escrevi um código que permite ler um arquivo .obj e adicionei uma função de interseção raio-triângulo a ele. Agora, adicionar o pato à nossa cena deve ser bastante trivial:

Conclusão
Meu principal objetivo é mostrar projetos que são interessantes (e fáceis!) Para programar. Estou convencido de que, para se tornar um bom programador, é preciso fazer muitos projetos paralelos. Não conheço você, mas pessoalmente não me sinto atraído pelo software de contabilidade e pelo jogo do caça-minas, mesmo que a complexidade do código seja bastante comparável.
Poucas horas e duzentas e cinquenta linhas de código nos dão um traçador de raios. Quinhentas linhas do rasterizador de software podem ser executadas em alguns dias. Gráficos é muito legal para aprender a programação!