Clone Numpy

Um pequeno módulo para trabalhar com matrizes em Python sem usar bibliotecas de terceiros (um clone do NumPy, mas apenas em Python puro).

Foi solicitado aos trabalhos de casa da universidade que escrevessem um programa que calculasse as normas e decomposições da matriz, mas foi proibido o uso de bibliotecas de terceiros. A escolha da linguagem de programação não é limitada. Eu escolhi python (que foi um erro, porque é muito mais lento que Java e C / C ++) e, portanto, não posso usar o NumPy. No processo, tive que escrever funções para realizar operações com matrizes, funções para encontrar menores, determinantes etc. O resultado é uma mini biblioteca para trabalhar com matrizes.

Meu código python puro é muito mais lento que o NumPy, que faz os cálculos de C e Fortran (mais meu código não é otimizado).

O que o MatLOL pode:

• Soma, diferença e produto das matrizes
• Produto da matriz por número
• Transposição da matriz
• Matriz menor
• Determinante da matriz
• Matriz inversa
• Matriz de união
• Número da condição da matriz
• As primeiras, segundas (não finalizadas), normas euclidianas e de matriz infinita
• Solução da equação AX = B
• Decomposição LU
• Decomposição de Cholesky
• Método Seidel

Exemplos MathLOL

Importe o módulo:

# from mathlol import * from mathlol import mathlol 

Inicialização de matriz

 matrix = mathlol() matrix.set([[1, 2, 3], [4, 5, 6], [7, -8, 9]]) matrix.get() #   

Algumas operações de matriz

 matrix * 2 #     2 A = [[0, 0, 0], [0, 1, 0], [0, 0, 0]] #  2  matrix.dot(A) matrix * A matrix.transposition() #   matrix.minor(i = 0, j = 0) #   matrix.determinant() #   matrix.inverse() #   L, U = matrix.lu() # LU  matrix.seidel(b = [[5.0], [9.0], [1.0]]) #   

Também existem funções para trabalhar com vetores

 vector = mathlol() vector.set([1, 2, 3, 4, 5]) vector.checkvector() # ,     vector.norm1_vector() vector.norm2_vector() vector.norm3_vector() 

Outros exemplos

Desempenho do MathLOL

Vamos ver a velocidade de computação de produtos de matrizes de tamanho NxN. As matrizes são preenchidas com números inteiros aleatórios de -100 a 100.




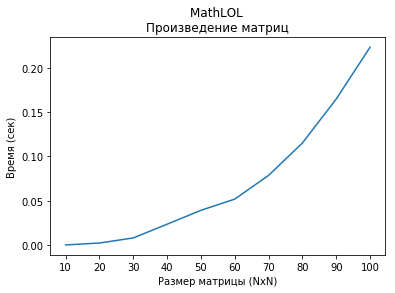
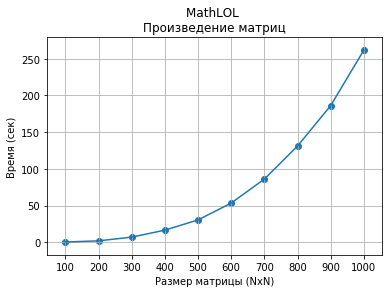
A velocidade da computação de tamanhos de produtos matriciais de 100x100 a 1000x1000



Compare a velocidade computacional de numpy e mathlol. Infelizmente, o mathlol foi muito lento e eu decidi levar matrizes para tamanhos de 100x100 a 1000x1000 para numpy e de 10x10 a 100x100 para mathlol.



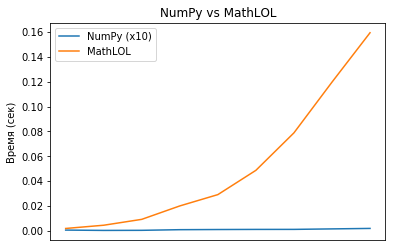
MathLOL calculou o produto da matriz 100x100 sozinho em 0,16 segundos, e NumPy calculou o produto da matriz 1000x1000 sozinho em 0,002 (!!!) segundos. A diferença é enorme.

Nossa tarefa era simplesmente implementar várias funções para trabalhar com matrizes, o que fizemos, mas o programa com matrizes grandes não funciona tão rápido quanto gostaríamos. Resta refinar o programa, adicionar mais algumas funções (por exemplo, uma função para calcular o número de Todd). Ficaria muito grato se você olhar o código, apontar erros e talvez ajudar a refinar o código.

Isso é tudo, o código e os exemplos são publicados no github .

PS No processo de redação do artigo, eu queria experimentar e incorporar C / C ++ no meu módulo. Eu cuidarei disso em um futuro próximo e ver quão próximo será o desempenho do NumPy.