
Em outubro, foi realizado o segundo campeonato de programação. Recebemos 12.500 inscrições, mais de 6.000 pessoas experimentaram competições. Dessa vez, os participantes podem escolher uma das seguintes faixas: back-end, front-end, desenvolvimento móvel e aprendizado de máquina. Em cada pista, era necessário passar na fase de qualificação e na final.
Por tradição, publicaremos análises de faixas no Habré. Vamos começar com as tarefas da fase de qualificação do aprendizado de máquina. A equipe preparou cinco tarefas, das quais havia duas opções para três: na primeira versão, as tarefas A1, B1 e C, na segunda - A2, B2 e C. As opções foram distribuídas aleatoriamente entre os participantes. O autor da tarefa C é nosso desenvolvedor Pavel Parkhomenko, o restante das tarefas foi feito por sua colega Nikita Senderovich.
Para a primeira tarefa algorítmica simples (A1 / A2), os participantes poderiam obter 50 pontos enumerando corretamente a resposta. Para a segunda tarefa (B1 / B2), de 10 a 100 pontos, dependendo da eficácia da solução. Para obter 100 pontos, foi necessário implementar o método de programação dinâmica. A terceira tarefa foi dedicada à construção de um modelo de clique com base nos dados de treinamento fornecidos. É necessário aplicar métodos de trabalho com atributos categóricos e usar um modelo não linear de treinamento (por exemplo, aumento de gradiente). Para a tarefa, você pode obter até 150 pontos - dependendo do valor da função de perda na amostra de teste.
A1 Restaurar o comprimento do carrossel
Condição
O sistema de recomendação deve determinar efetivamente os interesses das pessoas. Além dos métodos de aprendizado de máquina, soluções especiais de interface são usadas para executar esta tarefa, que pergunta explicitamente ao usuário o que é interessante para ele. Uma dessas soluções é o carrossel.
Um carrossel é uma faixa horizontal de cartões, cada um dos quais se oferece para assinar uma fonte ou tópico específico. O mesmo cartão pode ser encontrado no carrossel várias vezes. O carrossel pode ser rolado da esquerda para a direita, enquanto após o último cartão o usuário vê novamente o primeiro. Para o usuário, a transição do último cartão para o primeiro é invisível; do ponto de vista dele, a fita é interminável.
Em algum momento, um usuário curioso Vasily notou que a fita estava realmente presa e decidiu descobrir o comprimento real do carrossel. Para fazer isso, ele começou a rolar a fita e escrever seqüencialmente os cartões de reunião, para simplificar, designando cada cartão com uma letra latina minúscula. Então Vasily escreveu os primeiros n cartões em um pedaço de papel. É garantido que ele olhou para todos os cartões de carrossel pelo menos uma vez. Vasily foi para a cama e, pela manhã, descobriu que alguém havia derramado um copo de água em suas anotações e agora algumas cartas não podiam ser reconhecidas.
De acordo com as informações restantes, ajude Vasily a determinar o menor número possível de cartões no carrossel.
Formatos e exemplos de E / SFormato de entrada
A primeira linha contém um único número inteiro n (1 ≤ n ≤ 1000) - o número de caracteres escritos por Vasily.
A segunda linha contém a sequência escrita por Vasily. Consiste em n caracteres - letras latinas minúsculas e o sinal #, o que significa que a letra nesta posição não pode ser reconhecida.
Formato de saída
Imprima um único número positivo inteiro - o menor número possível de cartões no carrossel.
Exemplo 1
Exemplo 2
Exemplo 3
Exemplo 4
Anotações
No primeiro exemplo, todas as letras foram reconhecidas, o carrossel mínimo poderia consistir em 3 cartões - abc.
No segundo exemplo, todas as letras foram reconhecidas, o carrossel mínimo poderia consistir em 3 cartões - abb. Observe que o segundo e o terceiro cartões neste carrossel são os mesmos.
No terceiro exemplo, o menor comprimento possível do carrossel é obtido se assumirmos que o símbolo a estava na terceira posição. Então a linha inicial é ababa, o carrossel mínimo consiste em 2 cartões - ab.
No quarto exemplo, a cadeia de origem pode ser qualquer coisa, por exemplo, ffffff. Então o carrossel poderia consistir em um cartão - f.
Sistema de classificação
Somente depois de passar em todos os testes da tarefa você poderá obter
50 pontos .
No sistema de teste, os testes 1 a 4 são exemplos da condição.
Solução
Foi o suficiente para separar o comprimento possível do carrossel de 1 a n e, para cada comprimento fixo, verificar se era possível. É claro que a resposta sempre existe, uma vez que o valor de n é garantido como uma resposta possível. Para um comprimento fixo de carrossel p, basta verificar que na seqüência de caracteres transmitida para todos os i de 0 a (p - 1) em todas as posições i, i + p, i + 2p, etc., os mesmos caracteres ou # são encontrados. Se pelo menos para alguns i, existem 2 caracteres diferentes no intervalo de a a z, o carrossel não pode ter o comprimento p. Como na pior das hipóteses, para cada p, você precisa executar todos os caracteres da string uma vez, a complexidade desse algoritmo é O (n
2 ).
def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break
A2 Restaurar o comprimento do carrossel
Condição
O sistema de recomendação deve determinar efetivamente os interesses das pessoas. Além dos métodos de aprendizado de máquina, soluções especiais de interface são usadas para executar esta tarefa, que pergunta explicitamente ao usuário o que é interessante para ele. Uma dessas soluções é o carrossel.
Um carrossel é uma faixa horizontal de cartões, cada um dos quais se oferece para assinar uma fonte ou tópico específico. O mesmo cartão pode ser encontrado no carrossel várias vezes. O carrossel pode ser rolado da esquerda para a direita, enquanto após o último cartão o usuário vê novamente o primeiro. Para o usuário, a transição do último cartão para o primeiro é invisível; do ponto de vista dele, a fita é interminável.
Em algum momento, um usuário curioso Vasily notou que a fita estava realmente presa e decidiu descobrir o comprimento real do carrossel. Para fazer isso, ele começou a rolar a fita e escrever seqüencialmente os cartões de reunião, para simplificar, designando cada cartão com uma letra latina minúscula. Então Vasily escreveu os primeiros n cards. É garantido que ele olhou para todos os cartões de carrossel pelo menos uma vez. Como Vasily estava distraído com o conteúdo dos cartões, ao escrever, ele poderia substituir por engano uma letra por outra, mas sabe-se que no total ele não cometeu mais que k erros.
As gravações feitas por Vasily caíram em suas mãos; você também conhece o valor de k. Determine quão poucas cartas poderiam estar em seu carrossel.
Formatos e exemplos de E / SFormato de entrada
A primeira linha contém dois números inteiros: n (1 ≤ n ≤ 500) - o número de caracteres escritos por Basil, ek (0 ≤ k ≤ n) - o número máximo de erros que Vasily cometeu.
A segunda linha contém n letras minúsculas do alfabeto latino - a sequência escrita por Vasily.
Formato de saída
Imprima um único número positivo inteiro - o menor número possível de cartões no carrossel.
Exemplo 1
Exemplo 2
Exemplo 3
Exemplo 4
Anotações
No primeiro exemplo, k = 0, e sabemos com certeza que Vasily não se enganou, o carrossel mínimo poderia consistir em 3 cartões - abc.
No segundo exemplo, o menor comprimento possível do carrossel é obtido se assumirmos que Vasily substituiu por engano a terceira letra a por c. Então a linha real é ababa, o carrossel mínimo consiste em 2 cartões - ab.
No terceiro exemplo, sabe-se que Vasily poderia cometer um erro. No entanto, o tamanho do carrossel é mínimo, assumindo que ele não cometeu erros. O carrossel mínimo consiste em 3 cartões - abb. Observe que o segundo e o terceiro cartões neste carrossel são os mesmos.
No quarto exemplo, podemos dizer que Vasily estava errado ao digitar todas as letras, e a linha original poderia realmente ser qualquer uma, por exemplo, ffffff. Então o carrossel poderia consistir em um cartão - f.
Sistema de classificação
Somente depois de passar em todos os testes da tarefa você poderá obter
50 pontos .
No sistema de teste, os testes 1 a 4 são exemplos da condição.
Solução
Foi o suficiente para separar o comprimento possível do carrossel de 1 a n e, para cada comprimento fixo, verificar se era possível. É claro que a resposta sempre existe, uma vez que o valor de n é garantido como uma resposta possível, qualquer que seja o valor de k. Para um comprimento fixo de carrossel p, basta calcular, independentemente para todos os i, de 0 a (p - 1), qual é o número mínimo de erros cometidos nas posições i, i + p, i + 2p, etc. Esse número de erros é mínimo se considerado verdadeiro o símbolo é o que é encontrado nessas posições com mais frequência. Então, o número de erros é igual ao número de posições em que outra letra está. Se para alguns p o número total de erros não exceder k, o valor p é uma resposta possível. Como para cada p você precisa revisar todos os caracteres da string uma vez, a complexidade desse algoritmo é O (n
2 ).
n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break
B1 Fita de recomendação ideal
Condição
A formação da próxima parte da emissão pessoal de recomendações para o usuário não é uma tarefa fácil. Considere n publicações selecionadas a partir de uma base de recomendações com base na seleção de candidatos. O número de publicação i é caracterizado por uma pontuação de relevância si e um conjunto de k atributos binários
a1 ,
a2 , ...,
ak . Cada um desses atributos corresponde a alguma propriedade da publicação, por exemplo, se o usuário está inscrito na origem desta publicação, se a publicação foi criada nas últimas 24 horas etc. A publicação pode ter várias dessas propriedades ao mesmo tempo, caso em que os atributos correspondentes assumem o valor 1 ou pode não ter nenhum deles - e todos os seus atributos são 0.
Para que o feed do usuário seja diversificado, é necessário escolher entre m candidatos e publicações, para que entre eles haja pelo menos publicações A1 com a primeira propriedade, pelo menos publicações A2 com a segunda propriedade, ... publicações Publicações com a propriedade de número k. Encontre a pontuação máxima possível de relevância total para m publicações que atendam a esse requisito ou determine que esse conjunto de publicações não existe.
Formatos e exemplos de E / SFormato de entrada
A primeira linha contém três números inteiros - n, m, k (1 ≤ n ≤ 50, 1 ≤ m ≤ min (n, 9), 1 ≤ k ≤ 5).
As próximas n linhas mostram as características das publicações. A i-ésima publicação recebe um número inteiro s
i (1 ≤ s
i ≤ 10
9 ) - uma avaliação da relevância desta publicação e, em seguida, um espaço de k caracteres, cada um dos quais é 0 ou 1, é o valor de cada um dos atributos desta publicação.
A última linha contém k números inteiros separados por espaços - os valores A
1 , ..., A
k (0 ≤ A
i ≤ m) que definem os requisitos para o conjunto final de m publicações.
Formato de saída
Se não houver um conjunto de m publicações que satisfaçam as restrições, imprima o número 0. Caso contrário, imprima um único número inteiro positivo - a pontuação máxima possível de relevância total.
Exemplo 1
Exemplo 2
Anotações
No primeiro exemplo, de quatro publicações com duas propriedades, duas devem ser selecionadas para que haja pelo menos uma publicação que tenha a primeira propriedade e uma que tenha a segunda propriedade. A maior quantidade de relevância pode ser obtida se fizermos a segunda e a terceira publicações, embora qualquer opção com uma quarta publicação também seja adequada para restrições.
No segundo exemplo, é impossível selecionar duas publicações para que ambas tenham a segunda propriedade, porque somente a primeira publicação a possui.
Sistema de classificação
Os testes para esta tarefa consistem em cinco grupos. Os pontos para cada grupo são concedidos somente ao passar em todos os testes do grupo e em todos os testes dos grupos
anteriores . É necessário passar nos testes nas condições para obter pontos para grupos a partir do segundo. No total para a tarefa, você pode obter
100 pontos .
No sistema de teste, os testes 1-2 são exemplos da condição.
1.
(10 pontos) testes 3-10: k = 1, m ≤ 3, s
i ≤ 1000, nenhum teste é necessário a partir da condição
2.
(20 pontos) testes 11-20: k ≤ 2, m ≤ 3
3.
(20 pontos) testes 21–29: k ≤ 2
4.
(20 pontos) testa 30-37: k ≤ 3
5.
(30 pontos) testes 38–47: sem restrições adicionais
Solução
Existem n publicações, cada uma com velocidade e k sinalizadores booleanos, é necessário selecionar m cartões de forma que a soma de relevância seja máxima e k requisitos do formulário “entre as m publicações selecionadas devem ter ≥ cartões A
i com o i-ésimo sinalizador” sejam cumpridos ou determinar esse conjunto de publicações não existe.
A decisão é de 10 pontos : se houver exatamente uma bandeira, é suficiente receber publicações A
1 com essa bandeira que são de maior relevância (se houver menos cartas desse tipo que A
1 , o conjunto desejado não existe) e o restante (m - A
1 ) será ocupado pelas demais. cartões com a melhor relevância.
A decisão é de 30 pontos : se m não exceder 3, você poderá encontrar a resposta pesquisando exaustivamente todas as O (n
3 ) triplas de cartas possíveis, escolha a melhor opção em termos de relevância total que atenda às restrições.
A decisão é de 70 pontos (50 pontos é o mesmo, apenas mais fácil de implementar): se não houver mais de 3 sinalizadores, você poderá dividir todas as publicações em 8 grupos separados de acordo com o conjunto de sinalizadores que eles possuem: 000, 001, 010, 011, 100, 101, 110, 111. As publicações de cada grupo devem ser classificadas em ordem decrescente de relevância. Depois, você pode separar O (m
4 ) de quantas publicações melhores tiramos dos grupos 111, 011, 110 e 101. De cada uma, pegamos de 0 a m publicações, no total não mais que m. Depois disso, fica claro quantas publicações precisam ser coletadas dos grupos 100, 010 e 001 para atender aos requisitos. Resta chegar a m com os cartões restantes com a melhor relevância.
Solução completa : considere a função de programação dinâmica dp [i] [a] ... [z]. Essa é a pontuação máxima de relevância total que pode ser obtida usando exatamente as publicações i, para que exista exatamente uma publicação com a bandeira A, ..., z publicações com a bandeira Z. Então, inicialmente dp [0] [0] ... [0] = 0, e para todos os outros conjuntos de parâmetros, definimos o valor igual a -1 para maximizar esse valor no futuro. A seguir, "entraremos no jogo" cartões um de cada vez e usaremos cada cartão para melhorar os valores dessa função: para cada estado de dinâmica (i, a, b, ..., z) usando a j-ésima publicação com sinalizadores (a
j , b
j , ..., z
j ), podemos tentar fazer uma transição para o estado (i + 1, a + a
j , b + b
j , ..., z + z
j ) e verificar se o resultado melhora nesse estado. Importante: durante a transição, não estamos interessados em estados onde i ≥ m, portanto, os estados totais dessa dinâmica não são mais que m
k + 1 e o comportamento assintótico resultante é O (nm
k + 1 ). Quando os estados da dinâmica são calculados, a resposta é um estado que satisfaz as restrições e fornece a maior pontuação total de relevância.
Do ponto de vista da implementação, é útil armazenar o estado da programação dinâmica e os sinalizadores de cada publicação em formato compactado em um número inteiro para acelerar o trabalho do programa (consulte o código) e não em uma lista ou tupla. Esta solução utiliza menos memória e permite atualizar efetivamente o estado da dinâmica.
Código completo da solução:
def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score)
B2 Aproximação de funções
Condição
Para avaliar o grau de relevância dos documentos, vários métodos de aprendizado de máquina são usados - por exemplo, árvores de decisão. A árvore de decisão k-ária possui uma regra de decisão em cada nó que divide objetos em k classes de acordo com os valores de algum atributo. Na prática, geralmente são usadas árvores de decisão binária. Considere uma versão simplificada do problema de otimização, que deve ser resolvida em cada nó da árvore de decisão k-ary.
Seja definida uma função discreta f nos pontos i = 1, 2, ..., n. É necessário encontrar uma função constante por partes g que consiste em não mais que k seções de constância, de modo que o valor SSE =
[ ] (g (i) - f (i))
2 é mínimo.
Formatos e exemplos de E / SFormato de entrada
A primeira linha contém dois números inteiros n e k (1 ≤ n ≤ 300, 1 ≤ k ≤ min (n, 10)).
A segunda linha contém n números inteiros f (1), f (2), ..., f (n) - os valores da função aproximada nos pontos 1, 2, ..., n (–10
6 ≤ f (i) ≤ 10
6 ).
Formato de saída
Imprima um único número - o valor mínimo possível de SSE. A resposta é considerada correta se o erro absoluto ou relativo não exceder 10
–6 .
Exemplo 1
Exemplo 2
Exemplo 3
Anotações
No primeiro exemplo, a função ótima g é a constante g (i) = 2.
SSE = (2 - 1)
2 + (2 - 2)
2 + (2 - 3)
2 = 2.
No segundo exemplo, existem 2 opções. G (1) = 1 e g (2) = g (3) = 2,5 ou g (1) = g (2) = 1,5 e
g (3) = 3. Em qualquer caso, SSE = 0,5.
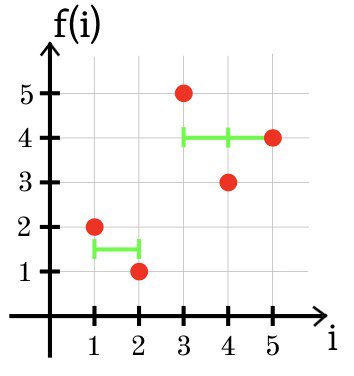
No terceiro exemplo, a aproximação ideal da função f usando duas seções de constância é mostrada abaixo: g (1) = g (2) = 1,5 eg (3) = g (4) = g (5) = 4.
SSE = (1,5 + 2)
2 + (1,5 - 1)
2 + (4-5)
2 + (4-3)
2 + (4-4)
2 = 2,5.
Sistema de classificação
Os testes para esta tarefa consistem em cinco grupos. Os pontos para cada grupo são concedidos somente ao passar em todos os testes do grupo e em todos os testes dos grupos
anteriores . É necessário passar nos testes nas condições para obter pontos para grupos a partir do segundo. No total para a tarefa, você pode obter
100 pontos .
No sistema de teste, os testes 1 a 3 são exemplos da condição.
1.
(10 pontos) testes 4-22: k = 1, não são necessários testes a partir da condição
2.
(20 pontos) testes 23–28: k ≤ 2
3.
(20 pontos) testa 29-34: k ≤ 3
4.
(20 pontos) testa 35-40: k ≤ 4
5.
(30 pontos) testes 41–46: sem restrições adicionais
Solução
Como você sabe, a constante que minimiza o valor SSE para um conjunto de valores f
1 , f
2 , ..., f
n é a média dos valores listados aqui. Além disso, como é fácil verificar por cálculos simples, o valor SSE =
soma \ quadrado \ valores \ - \ frac {quadrado \ soma \ valores} {n .
A decisão é de 10 pontos : simplesmente consideramos a média de todos os valores da função e SSE como O (n).
A decisão é de 30 pontos : separamos o último ponto relacionado à primeira parte da constância dos dois; para uma partição fixa, calculamos o SSE e selecionamos o ideal. Além disso, é importante não esquecer de desmontar o caso quando houver apenas uma seção de constância. Dificuldade - O (n
2 ).
A decisão é de 50 pontos : classificamos os limites da divisão em seções de constância para O (n
2 ); para uma partição fixa em 3 segmentos, calculamos o SSE e escolhemos o ideal. Dificuldade - O (n
3 ).
A decisão é de 70 pontos : calculamos as somas e somas de quadrados dos valores de
i nos prefixos, isso permitirá que você calcule rapidamente a média e o SSE em qualquer segmento. Classificamos os limites da partição em 4 seções de constância para O (n
3 ). Usando os valores pré-calculados nos prefixos de O (1), calculamos o SSE. Dificuldade - O (n
3 ).
Solução completa : considere a função de programação dinâmica dp [s] [i]. Esse é o menor valor do SSE se aproximarmos os primeiros valores de i usando os segmentos s. Então
dp [0] [0] = 0 e, para todos os outros conjuntos de parâmetros, definimos o valor igual ao infinito para minimizar ainda mais esse valor. Vamos resolver o problema, aumentando gradualmente o valor de s. Como calcular dp [s] [i] se os valores dinâmicos para todos os s menores já estiverem calculados? É suficiente designar para t o número de primeiros pontos cobertos pelos segmentos anteriores (s - 1) e classificar todos os valores de te aproximar os pontos restantes (i - t) usando o segmento restante. É necessário escolher o melhor valor t para o SSE final em i pontos. Se calcularmos a soma e a soma dos quadrados dos valores de f
i nos prefixos, essa aproximação será realizada em O (1), e o valor dp [s] [i] pode ser calculado em O (n). A resposta final é dp [k] [n]. A complexidade total do algoritmo é O (kn
2 ).
Código completo da solução:
n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n])
C. Previsão de cliques do usuário
Condição
Um dos sinais mais importantes para um sistema de recomendação é o comportamento do usuário. , .
..
2 : (train.csv) (test.csv). , . :
— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .
.
, item, publisher, user, topic .
csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.
logloss.
150 . logloss :
logloss . 2 , logloss 4 .
/train.csv:
test.csv:
:
Anotações
:
yadi.sk/d/pVna8ejcnQZK_A . , .
logloss :
EPS = 1e-4
def logloss(y_true, y_pred):
if abs (y_pred - 1) < EPS:
y_pred = 1 - EPS
if abs (y_pred) < EPS:
y_pred = EPS
return -y_true ∗ log(y_pred) - (1 - y_true) ∗ log(1 - y_pred)logloss logloss .
logloss :
def score(logloss):
if logloss > 0.5:
return 0.0
return min(150, (200 ∗ (0.5 - logloss)) ∗∗ 2) , . . , (, , , ) , — , - , .
, 100 ( 150).
— CatBoost . CatBoost ( ), . , . , -:
[ ]( ) , , , , - ( ).
. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).
,
ML- .