Camada convolucional: convolução rápida de acordo com o método de Shmuel Vinograd

1. Introdução

Este artigo é uma continuação de uma série de artigos que descrevem os algoritmos subjacentes.
O Synet é uma estrutura para o lançamento de redes neurais pré-treinadas na CPU.

Em um artigo anterior , descrevi métodos baseados na multiplicação de matrizes. Esses métodos com o mínimo esforço podem atingir, em muitos casos, mais de 80% do máximo teórico. Parece, bem, onde podemos melhorá-lo? Acontece que você pode! Existem métodos matemáticos que podem reduzir o número de operações necessárias para a convolução. Vamos nos familiarizar com um desses métodos, o algoritmo de convolução pelo método Vinograd, neste artigo.


Shmuel Winograd 1936.01.04 - 2019.03.25 - um destacado cientista da computação israelense e americano, criador de algoritmos para multiplicação matricial rápida, convolução e transformação de Fourier.

Um pouco de matemática

Embora, no aprendizado de máquina, as convoluções com um núcleo quadrado sejam usadas com mais frequência, para simplificar a apresentação, consideraremos primeiro o caso unidimensional. Suponha que tenhamos uma imagem unidimensional de tamanho $$$1 \ times4$ :

$$

$$d = \ begin {bmatrix} d_0 & d_1 & d_2 & d_3 \ end {bmatrix} ^ T,$$

e tamanho do filtro $$$1 \ times3$ :

$$

$$g = \ begin {bmatrix} g_0 & g_1 & g_2 \ end {bmatrix} ^ T,$$

então o resultado da convolução será:

$$

$$F (2,3) = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix}.$$

Essas expressões serão reescritas convenientemente na forma de matriz:

$$

$$F (2,3) = \ begin {bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \ end {bmatrix} \ begin {bmatrix} g_0 \\ g_1 \\ g_2 \ end {bmatrix} = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix} = \ begin {bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4 \ end {bmatrix}, (1)$$

onde a notação é usada:

$$

$$m_1 = (d_0-d_2) g_0, \\ m_2 = (d_1 + d_2) \ frac {g_0 + g_1 + g_2} {2}, \\ m_3 = (d_2-d_1) \ frac {g_0-g_1 + g_2} {2}, \\ m_4 = (d_1-d_3) g_2.$$

À primeira vista, a última substituição parece um pouco inútil - há claramente mais operações. Mas as expressões $$$\ frac {g_0 + g_1 + g_2} {2}$ e $$$\ frac {g_0-g_1 + g_2} {2}$ só precisa ser calculado uma vez. Com isso em mente, precisamos executar apenas 4 operações de multiplicação, enquanto na fórmula original elas precisam ser realizadas 6.
Reescrevemos a expressão (1):

$$

$$F (2,3) = A ^ T [(G g) \ odot (B ^ T d)], (2)$$

onde $$$\ odot$ denota multiplicação por elementos e a seguinte notação também é usada:

$$

$$B ^ T = \ begin {bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \ end { bmatrix}, (3) \\ G = \ begin {bmatrix} 1 & 0 & 0 \\ \ frac {1} {2} e \ frac {1} {2} e \ frac {1} {2} \\ \ frac {1} {2} e - \ frac {1} {2} e \ frac {1} {2} \\ 0 & 0 & 1 \ end {bmatrix}, (4) \\ A ^ T = \ inicie {bmatrix} 1 e 1 e 1 e 0 \\ 0 e 1 & -1 & -1 \ end {bmatrix}. (5)$$

A expressão (2) pode ser generalizada para o caso bidimensional:

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A. (6)$$

O número necessário de operações de multiplicação para $$$F (2 \ times2,3 \ times3)$ encolher de $$$2 \ times2 \ times3 \ times3 = 36$ antes $$$4 \ times4 = 16$ . Assim, obtemos o ganho computacional em $$$\ frac {36} {16} = $ 2,2$ vezes. Se você visualizar, na verdade nós, em vez de calcularmos separadamente a convolução para cada ponto da imagem, calcularemos imediatamente para um bloco de tamanho $$$2 \ times2$ :

Em qualquer caso, por convolução com a janela $$$r \ vezes s$ e tamanho do bloco $$$m \ vezes n$ o número de multiplicações necessárias será

$$

$$count = (m + r - 1) \ times (n + s - 1), (7)$$

e o ganho é descrito pela fórmula:

$$

$$k = \ frac {m \ times n \ times r \ times s} {(m + r - 1) \ times (n + s - 1)}. (8)$$

No limite, para quantidades suficientemente grandes $$$m$ e $$$n$ para qualquer convolução, apenas 1 operação de multiplicação por ponto é suficiente! Infelizmente, um aumento no tamanho do bloco leva a um rápido aumento na sobrecarga de entrada $$$B ^ T d B$ e fim de semana $$$A ^ T [...] A$ imagens, portanto, na prática, geralmente não use um tamanho de bloco maior que $$$4 \ times4$ .

Exemplo de implementação

Para a implementação prática do algoritmo Vinogrado, eu gostaria de considerar o caso mais simples - convolução com o kernel $$$3 \ times3$ para bloco $$$2 \ times2$ . Para simplificar ainda mais a apresentação, também assumimos que não há preenchimento da imagem de entrada e que os tamanhos das imagens de entrada e saída são múltiplos de 2.

A implementação da convolução baseada na multiplicação de matrizes será semelhante a:

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Quem quiser entender em detalhes o que está acontecendo aqui deve recorrer ao meu artigo anterior . A implementação atual é obtida a partir da anterior, se colocarmos:

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

Algoritmo de convolução modificado

Dou novamente aqui a fórmula (6):

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

Se você mudar do tamanho da imagem de saída $$$2 \ times2$ para uma imagem de tamanho arbitrário, então teremos que dividi-la em blocos de tamanho $$$2 \ times2$ . Para cada bloco, uma imagem de entrada será formada $$$(2 + 3 - 1) \ vezes (2 + 3 - 1) = $ 1$ valores incluídos em 16 convertidos $$$B ^ T d B$ imagens de entrada reduzidas pela metade do tamanho. Então, cada uma dessas 16 matrizes é multiplicada pela matriz correspondente dos pesos transformados $$$G g G ^ T$ . 16 matrizes resultantes são convertidas para a imagem de saída $$$A ^ T \ bigg [... \ bigg] A$ . Abaixo deste processo é desenhado no diagrama:



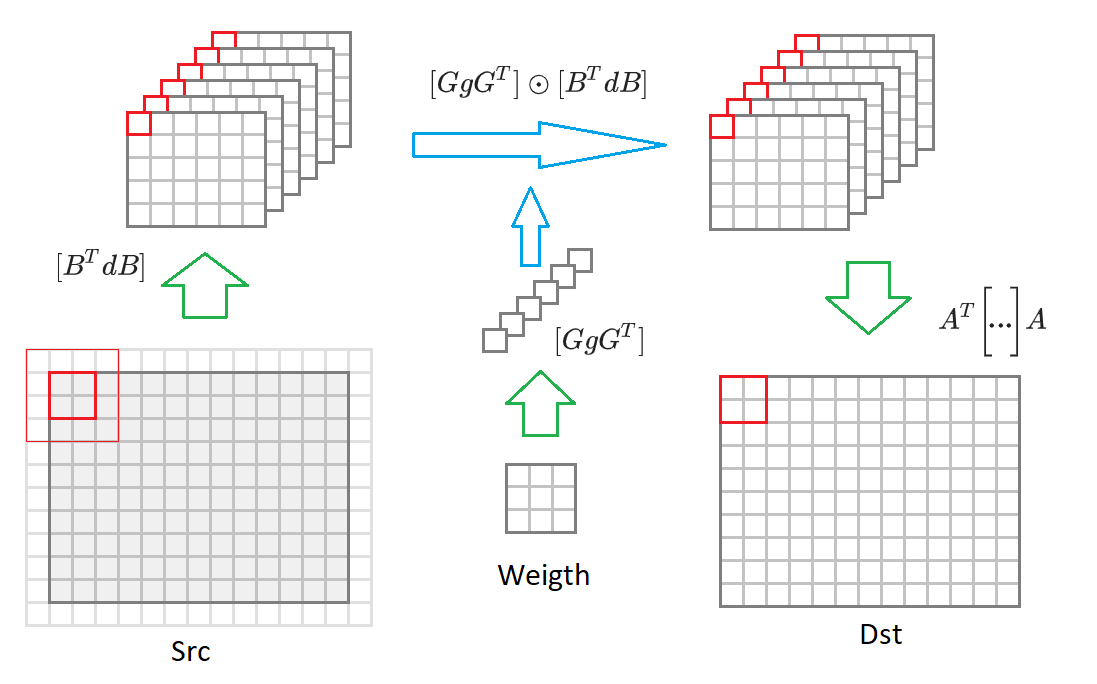
Diante desses comentários, o algoritmo de convolução assume a forma:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

O número de operações necessárias sem levar em consideração as transformações da imagem de entrada e saída: ~ srcC * dstC * dstH * dstW * count . A seguir, descrevemos os algoritmos para converter pesos, imagens de entrada e saída.

Converter escalas convolucionais

Como pode ser visto na expressão (6), a seguinte transformação deve ser realizada em pesos de convolução: $$$G g G ^ T$ onde está a matriz $$$G$ definido na expressão (4). O código para esta conversão terá a seguinte aparência:

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

Felizmente, essa conversão precisa ser feita apenas 1 vez. Portanto, não afeta o desempenho final.

Conversão de imagem de entrada

Como pode ser visto na expressão (6), a seguinte transformação deve ser realizada na imagem de entrada: $$$B ^ T d B$ onde está a matriz $$$B ^ T$ definido na expressão (3). O código para esta conversão terá a seguinte aparência:

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

O número de operações necessárias para esta conversão é: ~ srcH * srcW * srcC * count .

Conversão de imagem de saída

Como pode ser visto na expressão (6), a seguinte transformação deve ser realizada na imagem de saída: $$$A ^ T [...] A$ onde está a matriz $$$B ^ T$ definido na expressão (5). O código para esta conversão terá a seguinte aparência:

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

O número de operações necessárias para esta conversão é: ~ dstH * dstW * dstC * count .

Características da implementação prática

No exemplo acima, descrevemos o algoritmo Vinohrad para um bloco de tamanho $$$2 \ times2$ . Na prática, uma versão mais avançada do algoritmo é mais frequentemente usada: $$$F (4 \ times4,3 \ times3)$ . Nesse caso, o tamanho do bloco será $$$4 \ times4$ , e o número de matrizes transformadas é 36. O ganho computacional, de acordo com a fórmula (8), alcançará 4 . O esquema geral do algoritmo é o mesmo, apenas a matriz dos algoritmos de transformação diferem.

Há um pequeno projeto no Github que permite calcular essas matrizes com coeficientes para um tamanho arbitrário de kernel de convolução e tamanho de bloco.

Apresentamos uma variante do algoritmo Vinogrado para o formato de imagem NCHW , mas o algoritmo pode ser implementado de maneira semelhante ao formato NHWC (falei em mais detalhes sobre esses formatos de imagem no artigo anterior .

Apesar da presença de transformações adicionais, a principal carga computacional no algoritmo Vinogrado (com sua aplicação competente, é claro) ainda está na multiplicação da matriz. Felizmente, esta é uma operação padrão e é efetivamente implementada em muitas bibliotecas.

As funções de transformação otimizadas para diferentes plataformas para o algoritmo Vinohrad podem ser encontradas aqui .

Prós e contras do algoritmo da uva

Primeiro, é claro, os profissionais:

• O algoritmo permite várias vezes (na maioria das vezes 2-3 vezes) acelerar o cálculo da convolução. Assim, é possível calcular a convolução mais rapidamente do que o limite "teórico".
• O algoritmo baseia-se em sua implementação no algoritmo de multiplicação de matriz padrão.
• Pode ser implementado para vários formatos de imagem de entrada: NCHW , NHWC .
• O tamanho do buffer para armazenar valores intermediários é menor que o necessário para o algoritmo de multiplicação de matrizes.

Bem e onde sem desvantagens:

• O algoritmo requer uma implementação separada das funções de conversão para cada tamanho de kernel de convolução, bem como para cada tamanho de bloco. Talvez essa seja uma das principais razões pelas quais quase sempre é implementada apenas para convolução com o kernel. $$$3 \ times3$ .
• À medida que o tamanho do bloco aumenta, a complexidade da implementação das funções de conversão aumenta rapidamente. Portanto, praticamente não há implementações com um tamanho de bloco maior que $$$4 \ times4$ .
• O algoritmo impõe restrições estritas sobre os parâmetros de convolução strideY = strideY = dilataçãoY = dilataçãoX = grupo = 1 . Embora teoricamente seja possível implementar o algoritmo quando essas restrições forem violadas, na prática é pequeno aplicável devido à baixa eficiência.
• A eficiência do algoritmo diminui se o número de canais de entrada ou saída na imagem for pequeno (isso se deve ao custo da conversão das imagens de entrada e saída).
• A eficiência do algoritmo diminui para tamanhos pequenos de imagens de entrada (as matrizes resultantes da imagem de entrada são muito pequenas e o algoritmo de multiplicação de matriz padrão se torna ineficaz para elas).

Conclusões

O método de cálculo da convolução baseado no algoritmo Vinograd pode aumentar significativamente a eficiência computacional em comparação com o método baseado na multiplicação simples de matrizes. Infelizmente, não é universal e é difícil de implementar. Em vários casos especiais, existem abordagens mais rápidas, cuja descrição gostaria de adiar para os próximos artigos desta série . À espera de feedback e comentários dos leitores. Espero que você esteja interessado!

PS Esta e outras abordagens são implementadas por mim no Convolution Framework como parte da biblioteca Simd .
Essa estrutura é subjacente ao Synet , uma estrutura para executar redes neurais pré-treinadas na CPU.